2020-2021学年人教版八年级下册18.1.2平行四边形的判定第1课时课件(30张ppt)
文档属性
| 名称 | 2020-2021学年人教版八年级下册18.1.2平行四边形的判定第1课时课件(30张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 521.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 17:55:39 | ||
图片预览








文档简介
(共30张PPT)
平行四边形的判定
第1课时
八年级下册
学习目标
1.掌握平行四边形的判定方法;
2.培养用类比、逆向联想及运动的思维方法来研究问题
。
预习检测
在下列条件中,不能判定四边形是平行四边形的是(
)
AB∥CD,
AD∥BC
AB=CD,
AD=BC
(C)AB∥CD,
AB=CD
(D)
AB∥CD,
∠A=∠C
(E)
AB∥CD,
AD=BC
E
情境导入
他是根据平行四边形的定义:
两组对边分别平行的四边形是平行四边形。
有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
1、平行四边形的性质:
(1)从边看:两组对边_______;
两组对边_______;
(2)从角看:两组对角_______;
四组邻角_______;
(3)从对角线看:对角线______________。
相互平分
互补
相等
相等
平行
温故知新
2、平行四边形性质的逆命题:
(1)两组对边分别平行的四边形是平行四边形
(2)两组对边分别相等的四边形是______________
;
(3)两组对角______________的四边形是______________
;
(4)对角线______________的四边形是______________
。
猜想:这些逆命题成立吗?
可否成为平行四边形的判别方法?
平行四边形
平行四边形
平行四边形
分别相等
相互平分
成立
可以
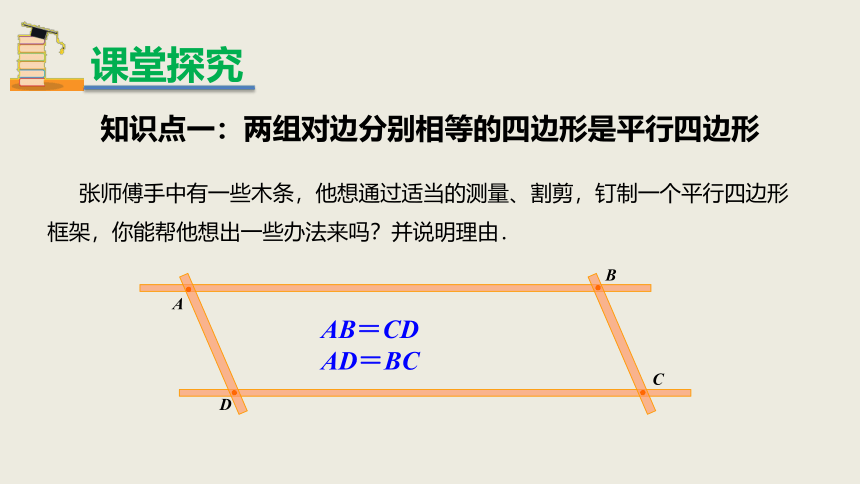
张师傅手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗?并说明理由.
●
●
●
●
A
C
B
D
AB=CD
AD=BC
课堂探究
知识点一:两组对边分别相等的四边形是平行四边形
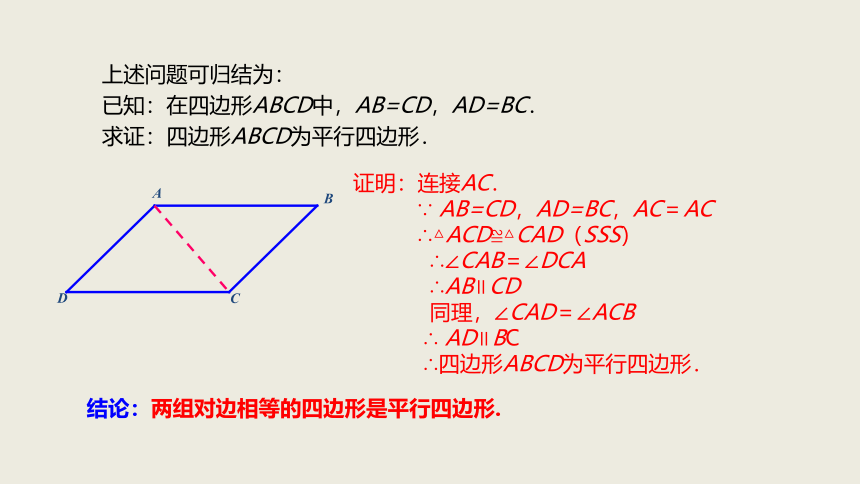
证明:连接AC.
∵
AB=CD,AD=BC,AC=AC
∴△ACD≌△CAD(SSS)
∴∠CAB=∠DCA
∴AB∥CD
同理,∠CAD=∠ACB
∴
AD∥BC
∴四边形ABCD为平行四边形.
上述问题可归结为:
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD为平行四边形.
A
C
B
D
结论:两组对边相等的四边形是平行四边形.
平行四边形判定:
方法一:两组对边分别平行的四边形是
平行四边形;(定义法)
几何语言:
如图,∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形;
方法二:两组对边分别相等的四边形是平行四边形;
几何语言:
如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形;
试一试(一)
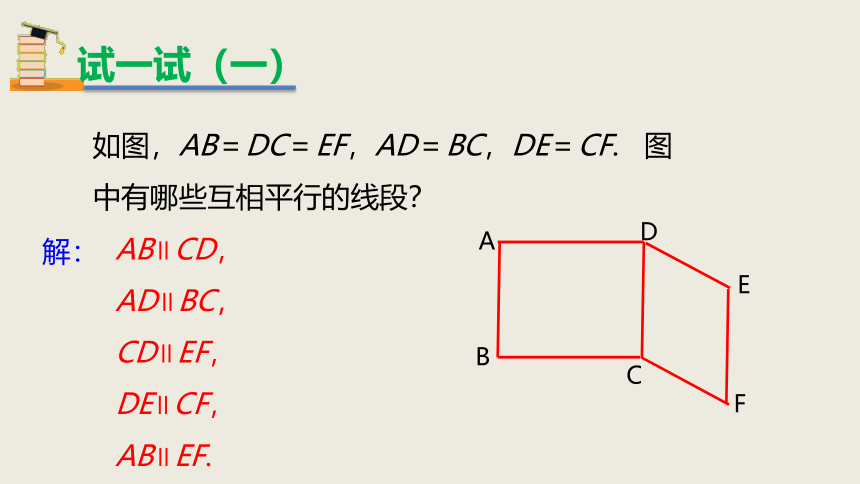
如图,AB=DC=EF,AD=BC,DE=CF.
图中有哪些互相平行的线段?
AB∥CD,AD∥BC,
CD∥EF,DE∥CF,
AB∥EF.
解:
A
B
C
D
E
F
课堂探究
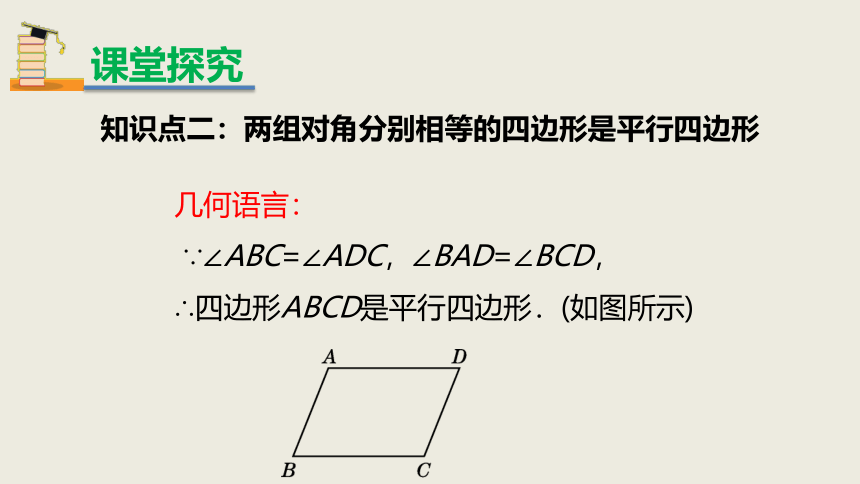
知识点二:两组对角分别相等的四边形是平行四边形
几何语言:
∵∠ABC=∠ADC,∠BAD=∠BCD,
∴四边形ABCD是平行四边形.(如图所示)
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
同理可证AB∥CD
又∵∠A+
∠B+
∠C+
∠D
=360
°
∴
2∠A+
2∠B=360
°
∵∠A=∠C,∠B=∠D(已知)
即∠A+∠B=180
°
∴
AD∥BC
(同旁内角互补,两直线平行)
结论:两组对角相等的四边形是平行四边形.
试一试(二)
如图,在?ABCD中,BE平分∠ABC,交AD于点E,DF平分∠ADC,交BC于点F,那么四边形BFDE是平行四边形吗?为什么?
解:四边形BFDE是平行四边形.
理由:在?ABCD中,∠ABC=∠ADC,∠A=∠C.
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE=∠CBE=
∠ABC,
∠CDF=∠ADF=
∠ADC,
∴∠CDF=∠ADF=∠ABE=∠CBE.
∵∠DFB=∠C+∠CDF,
∠BED=∠ABE+∠A,
∴∠DFB=∠BED,
∴四边形BFDE是平行四边形.
将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD
.想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
课堂探究
知识点三:对角线互相平分的四边形是平行四边形
△AOB≌△COD
→
∠BAC=∠ACD→AB∥CD
∠CAD=∠ACB→AD∥BC
同理,△BOC≌△AOD
→
四边形ABCD是平行四边形.
结论:两条对角线互相平分的四边形是平行四边形.
A
C
B
O
D
对角线互相平分的四边形是平行四边形.
几何语言:
如图,∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
例3
如图,口ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,且
AE=CF。求证:四边形BFDE是平行四边形。
证明:∵ABCD是平行四边形
O是对角线AC、BD交点
∴OA=OC
OB=OD
又∵AE=CF
∴OE=OF
∴四边形BFDE是平行四边形
例题解析
思考
你还有其它证明方法吗?
试一试(三)
如图,?ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中
点.
求证BE=DF.
解:∵四边形ABCD是平行四边形.
∴
BO=DO,OA=OC.
∵E,F分别是OA,OC的中点,
∴OE=
OA=
OC=OF.
又∵∠BOE=∠DOF,
∴△BOE≌△DOF,
∴BE=DF.
A
B
C
D
E
F
O
思考
我们知道,两组对边分别平行或相等的四边形是平行四边形,如果只考虑四边形的一组对边,它们满足什么条件对这个四边形能成为平行四边形呢?
知识点四:一组对边平行且相等的四边形是平行四边形
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
A
B
C
D
已知:在四边形ABCD中,
AD=BC,AD//BC.
求证:四边形ABCD是平行四边形.
你还有其他
证法吗?
课堂探究
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理:
几何语言:
∵AB
CD
∴四边形ABCD是平行四边形.
A
B
C
D
归纳
证明:
∵四边形ABCD是平行四边形
∵E,F分别是AD,BC的中点
∴ED
BF
∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴BE=DF(平行四边形的对边相等)
例4:已知:如图,E,F分别是□ABCD的边AD,
BC的中点。
求证:四边形EBFD是平行四边形
∴
ADBC(平行四边形的对边平行且相等)
例题解析
A
B
C
D
E
F
1、为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的
枕木长相等就可以了.
你能说出其中的道理吗?
因为一组对边平行且相等的四边形是平行四边形,
所以铁轨和夹在铁轨之间的枕木构成了平行四边形,
因此可知两条直铺的铁轨是互相平行的.
解:
试一试(四)
2、如图,在?
ABCD中,BD是它的一条对角线,过A,C两点分别作AE丄BD,
CF丄BD,E,F为垂足.
求证:四边形AFGE是平行四边形.
┌
A
B
C
D
E
F
┌
∵
四边形ABCD是平行四边形,
∴
AB∥CD,AB=CD,
∴
∠CDB=∠ABD.
又∵
AE⊥BD,CF⊥BD,
∴
∠AEB=∠CFD=90°,
∴
AE∥CF.
在△ABE和△CDF中,
AB=CD,∠ABE=∠CDF,∠AEB=∠CFD,
∴
△ABE≌△CDF,
∴
AE=CF.
又∵
AE∥CF,
∴四边形AFCE是平行四边形.
解:
2、四边形ABCD中,若∠A
=
∠C,∠B
=
∠D,则下列结论中错误的是(
)
随堂检测
B
C
1、能判定一个四边形是平行四边形的条件是(
)
A、一组对角相等
B、一组对边平行且相等
C、一对邻角互补
D、两条对角线互相垂直
A、AB
=
CD
B、AD∥BC
C、∠A
=
∠B
D、对角线互相平分
3、如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么
当BC=___?cm,CD=___?cm时,
四边形ABCD为平行四边形;
(2)若AC=6cm,BD=10cm,那么
当AO=___cm,DO=___cm时,
四边形ABCD为平行四边形.
5
3
4
8
4.如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
证明:
∵△ABD、△BCE、△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,
∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.
课堂小结
本节课我们学习了什么?你有什么收获呢?
平行四边形的判定方法
从边来判定
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
书面作业:完成相关书本作业
布置作业
再见
平行四边形的判定
第1课时
八年级下册
学习目标
1.掌握平行四边形的判定方法;
2.培养用类比、逆向联想及运动的思维方法来研究问题
。
预习检测
在下列条件中,不能判定四边形是平行四边形的是(
)
AB∥CD,
AD∥BC
AB=CD,
AD=BC
(C)AB∥CD,
AB=CD
(D)
AB∥CD,
∠A=∠C
(E)
AB∥CD,
AD=BC
E
情境导入
他是根据平行四边形的定义:
两组对边分别平行的四边形是平行四边形。
有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
1、平行四边形的性质:
(1)从边看:两组对边_______;
两组对边_______;
(2)从角看:两组对角_______;
四组邻角_______;
(3)从对角线看:对角线______________。
相互平分
互补
相等
相等
平行
温故知新
2、平行四边形性质的逆命题:
(1)两组对边分别平行的四边形是平行四边形
(2)两组对边分别相等的四边形是______________
;
(3)两组对角______________的四边形是______________
;
(4)对角线______________的四边形是______________
。
猜想:这些逆命题成立吗?
可否成为平行四边形的判别方法?
平行四边形
平行四边形
平行四边形
分别相等
相互平分
成立
可以
张师傅手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗?并说明理由.
●
●
●
●
A
C
B
D
AB=CD
AD=BC
课堂探究
知识点一:两组对边分别相等的四边形是平行四边形
证明:连接AC.
∵
AB=CD,AD=BC,AC=AC
∴△ACD≌△CAD(SSS)
∴∠CAB=∠DCA
∴AB∥CD
同理,∠CAD=∠ACB
∴
AD∥BC
∴四边形ABCD为平行四边形.
上述问题可归结为:
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD为平行四边形.
A
C
B
D
结论:两组对边相等的四边形是平行四边形.
平行四边形判定:
方法一:两组对边分别平行的四边形是
平行四边形;(定义法)
几何语言:
如图,∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形;
方法二:两组对边分别相等的四边形是平行四边形;
几何语言:
如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形;
试一试(一)
如图,AB=DC=EF,AD=BC,DE=CF.
图中有哪些互相平行的线段?
AB∥CD,AD∥BC,
CD∥EF,DE∥CF,
AB∥EF.
解:
A
B
C
D
E
F
课堂探究
知识点二:两组对角分别相等的四边形是平行四边形
几何语言:
∵∠ABC=∠ADC,∠BAD=∠BCD,
∴四边形ABCD是平行四边形.(如图所示)
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
同理可证AB∥CD
又∵∠A+
∠B+
∠C+
∠D
=360
°
∴
2∠A+
2∠B=360
°
∵∠A=∠C,∠B=∠D(已知)
即∠A+∠B=180
°
∴
AD∥BC
(同旁内角互补,两直线平行)
结论:两组对角相等的四边形是平行四边形.
试一试(二)
如图,在?ABCD中,BE平分∠ABC,交AD于点E,DF平分∠ADC,交BC于点F,那么四边形BFDE是平行四边形吗?为什么?
解:四边形BFDE是平行四边形.
理由:在?ABCD中,∠ABC=∠ADC,∠A=∠C.
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE=∠CBE=
∠ABC,
∠CDF=∠ADF=
∠ADC,
∴∠CDF=∠ADF=∠ABE=∠CBE.
∵∠DFB=∠C+∠CDF,
∠BED=∠ABE+∠A,
∴∠DFB=∠BED,
∴四边形BFDE是平行四边形.
将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD
.想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
课堂探究
知识点三:对角线互相平分的四边形是平行四边形
△AOB≌△COD
→
∠BAC=∠ACD→AB∥CD
∠CAD=∠ACB→AD∥BC
同理,△BOC≌△AOD
→
四边形ABCD是平行四边形.
结论:两条对角线互相平分的四边形是平行四边形.
A
C
B
O
D
对角线互相平分的四边形是平行四边形.
几何语言:
如图,∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
例3
如图,口ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,且
AE=CF。求证:四边形BFDE是平行四边形。
证明:∵ABCD是平行四边形
O是对角线AC、BD交点
∴OA=OC
OB=OD
又∵AE=CF
∴OE=OF
∴四边形BFDE是平行四边形
例题解析
思考
你还有其它证明方法吗?
试一试(三)
如图,?ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中
点.
求证BE=DF.
解:∵四边形ABCD是平行四边形.
∴
BO=DO,OA=OC.
∵E,F分别是OA,OC的中点,
∴OE=
OA=
OC=OF.
又∵∠BOE=∠DOF,
∴△BOE≌△DOF,
∴BE=DF.
A
B
C
D
E
F
O
思考
我们知道,两组对边分别平行或相等的四边形是平行四边形,如果只考虑四边形的一组对边,它们满足什么条件对这个四边形能成为平行四边形呢?
知识点四:一组对边平行且相等的四边形是平行四边形
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
A
B
C
D
已知:在四边形ABCD中,
AD=BC,AD//BC.
求证:四边形ABCD是平行四边形.
你还有其他
证法吗?
课堂探究
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理:
几何语言:
∵AB
CD
∴四边形ABCD是平行四边形.
A
B
C
D
归纳
证明:
∵四边形ABCD是平行四边形
∵E,F分别是AD,BC的中点
∴ED
BF
∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴BE=DF(平行四边形的对边相等)
例4:已知:如图,E,F分别是□ABCD的边AD,
BC的中点。
求证:四边形EBFD是平行四边形
∴
ADBC(平行四边形的对边平行且相等)
例题解析
A
B
C
D
E
F
1、为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的
枕木长相等就可以了.
你能说出其中的道理吗?
因为一组对边平行且相等的四边形是平行四边形,
所以铁轨和夹在铁轨之间的枕木构成了平行四边形,
因此可知两条直铺的铁轨是互相平行的.
解:
试一试(四)
2、如图,在?
ABCD中,BD是它的一条对角线,过A,C两点分别作AE丄BD,
CF丄BD,E,F为垂足.
求证:四边形AFGE是平行四边形.
┌
A
B
C
D
E
F
┌
∵
四边形ABCD是平行四边形,
∴
AB∥CD,AB=CD,
∴
∠CDB=∠ABD.
又∵
AE⊥BD,CF⊥BD,
∴
∠AEB=∠CFD=90°,
∴
AE∥CF.
在△ABE和△CDF中,
AB=CD,∠ABE=∠CDF,∠AEB=∠CFD,
∴
△ABE≌△CDF,
∴
AE=CF.
又∵
AE∥CF,
∴四边形AFCE是平行四边形.
解:
2、四边形ABCD中,若∠A
=
∠C,∠B
=
∠D,则下列结论中错误的是(
)
随堂检测
B
C
1、能判定一个四边形是平行四边形的条件是(
)
A、一组对角相等
B、一组对边平行且相等
C、一对邻角互补
D、两条对角线互相垂直
A、AB
=
CD
B、AD∥BC
C、∠A
=
∠B
D、对角线互相平分
3、如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么
当BC=___?cm,CD=___?cm时,
四边形ABCD为平行四边形;
(2)若AC=6cm,BD=10cm,那么
当AO=___cm,DO=___cm时,
四边形ABCD为平行四边形.
5
3
4
8
4.如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
证明:
∵△ABD、△BCE、△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,
∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.
课堂小结
本节课我们学习了什么?你有什么收获呢?
平行四边形的判定方法
从边来判定
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
书面作业:完成相关书本作业
布置作业
再见
