2020—2021学年人教版数学八年级下册 19.2.2.2一次函数的图象与性质课件(18张ppt)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册 19.2.2.2一次函数的图象与性质课件(18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 480.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 18:09:51 | ||
图片预览




文档简介
(共18张PPT)
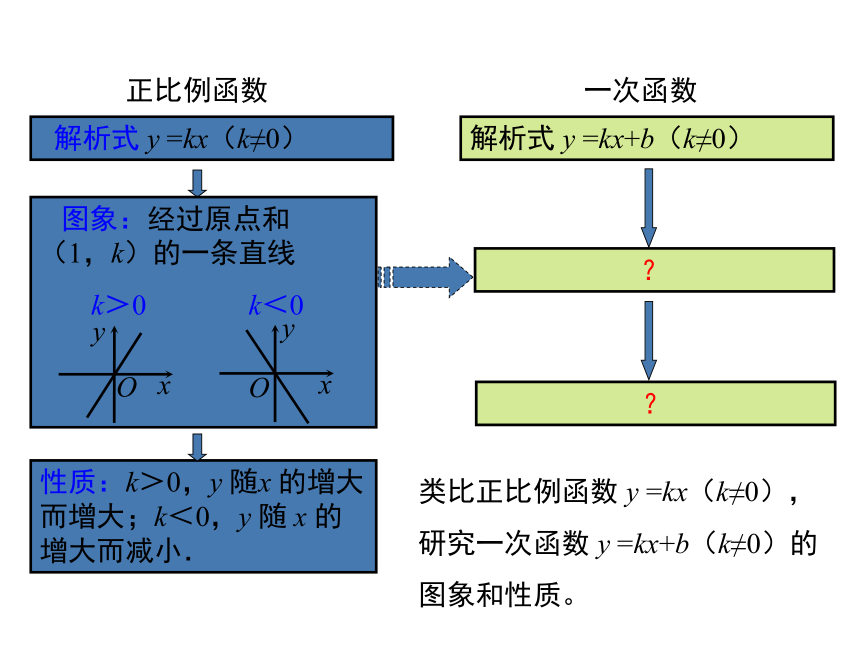
19.2.2.2一次函数的图象与性质
一、知识链接
形如
的函数,叫做一次函数;
3.正比例函数的图象是一条经过
点的
.
y=kx+b(k,b是常数,k≠0)
原
直线
2.画函数图象的步骤有
,
,
.
列表
描点
连线
(写解析式)
1.
什么是一次函数?
自主学习
正比例函数
解析式
y
=kx(k≠0)
性质:k>0,y
随x
的增大而增大;k<0,y
随
x
的增大而减小.
一次函数
解析式
y
=kx+b(k≠0)
类比正比例函数
y
=kx(k≠0),研究一次函数
y
=kx+b(k≠0)的图象和性质。
图象:经过原点和
(1,k)的一条直线
x
y
O
k>0
k<0
x
y
O
?
?
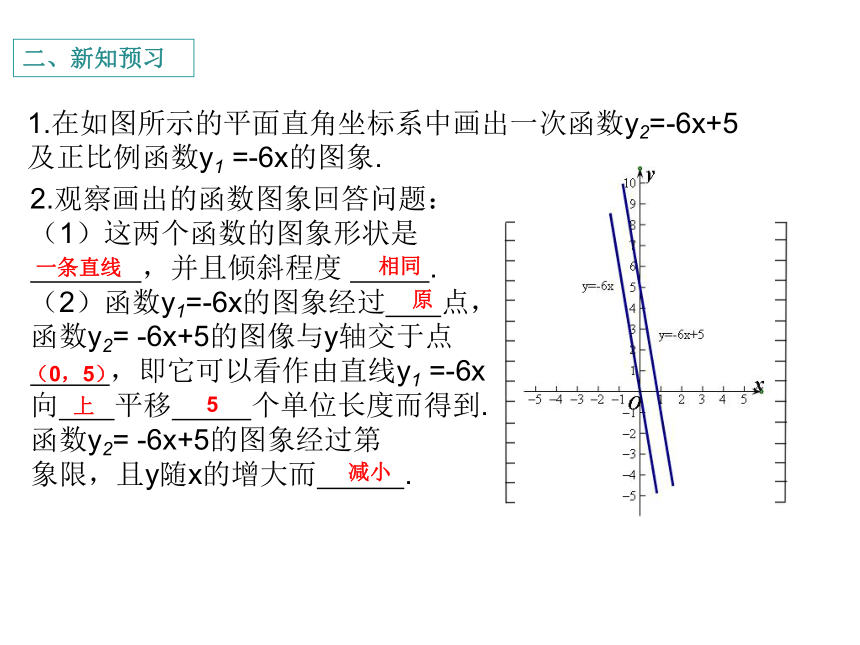
二、新知预习
1.在如图所示的平面直角坐标系中画出一次函数y2=-6x+5
及正比例函数y1
=-6x的图象.
2.观察画出的函数图象回答问题:
(1)这两个函数的图象形状是
,并且倾斜程度
.
(2)函数y1=-6x的图象经过
点,
函数y2=
-6x+5的图像与y轴交于点
,即它可以看作由直线y1
=-6x
向
平移
个单位长度而得到.
函数y2=
-6x+5的图象经过第
象限,且y随x的增大而
.
一条直线
相同
原
(0,5)
上
5
减小
3.自主归纳:
(1)当k>0时,y随x的增大而
,当k<0时,y随x的增大而
.
(2)一次函数y=kx+b的图象可以由正比例函数y=kx的图象沿y轴方向平移
个单位长度得到(当b>0时,
向
平移;当b<0时,向
平移).
增大
减小
上
下
三、自学自测
1.与一次函数y=2x-3的图象平行的是下列哪个函数的图象(
)
A.y=-x-3
B.y=2x+1
C.y=-2x
D.y=3x+3
2.下列一次函数中,y随x值的增大而减小的是(
)
A.
y=2x+1
B.
y=-4x+3
C.y=x+2
D.
y=(5-2)x
B
B
O
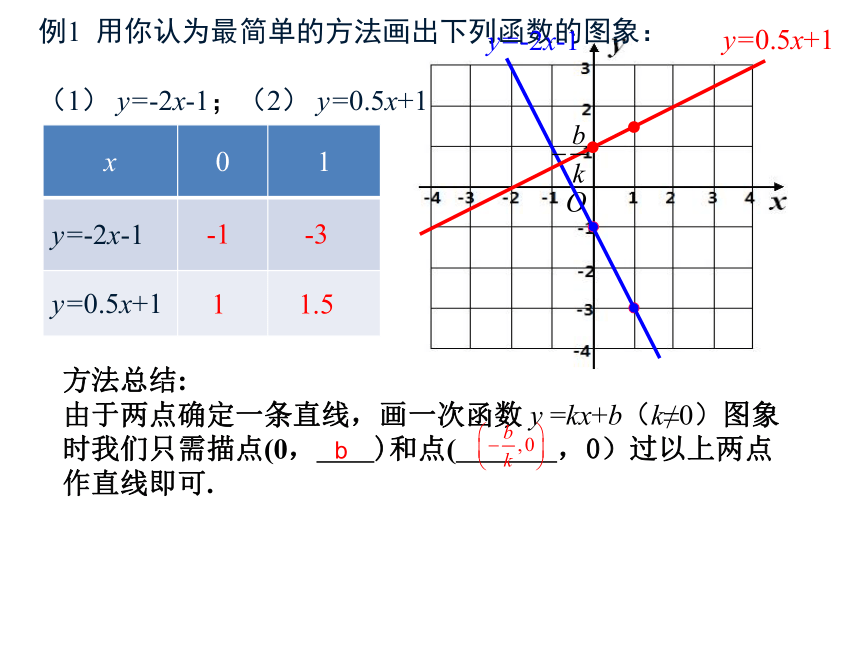
例1
用你认为最简单的方法画出下列函数的图象:
(1)
y=-2x-1;(2)
y=0.5x+1
x
0
1
y=-2x-1
y=0.5x+1
-1
-3
1
y=-2x-1
1.5
y=0.5x+1
方法总结:
由于两点确定一条直线,画一次函数
y
=kx+b(k≠0)图象时我们只需描点(0,
)和点(
,0)过以上两点作直线即可.
b
一次函数的性质
二
例2
在同一坐标系中画出下列一次函数的图象:
(1)y1
=x+2;
(2)y2
=2x-1;
(3)y3
=-x+2; (4)y4
=-2x-2.
思考:仿照正比例函数的做法,你能看出当
k
的符号
变化时,函数的增减性怎样变化吗?
要点归纳:
(1)当k>0时,图象从左到右呈
趋势,y随自变量x的增大而
;
①b>0时,直线经过第
象限;
②
b<0时,直线经过第
象限.
(2)当k<0时,图象从左到右呈
趋势,y随自变量x的增大而
.
①b>0时,直线经过第
象限;
②
b<0时,直线经过第
象限.
上升
增大
三、二、一
三、四、一
下降
减小
二、一、四
二、三、四
O
y1
=x+2
y2
=2x-1
O
y3=-x+2
y4
=-2x-2
五、合作提升
一次函数y=kx+b(k≠0)
图象
画一次函数图象时我们只需描点(0,b)和点(
,0)连线即可.(两点法)
k>0
k<0
b>0
b=0
b<0
b>0
b=0
b<0
图象是自左向右呈
趋势
图象是自左向右呈
趋势
经过第
象限
经过第
象限
经过第
象限
经过第
象限
经过第
象限
经过第
象限
|k|越大,图象越陡(即越靠近y轴)
性质
y随x的增大而
.
y随x的增大而
.
图象平移
一次函数y=kx+b(k≠0)的图象可以由正比例函数y=kx的图象沿y轴方向平移
个单位长度得到(当b>0时,向
平移;当b<0时,向
平移)
根据一次函数的图象判断k,b的正负,并说出直线经过的象限
k
0,b
0
>
>
k
0,b
0
k
0,b
0
k
0,b
0
k
0,b
0
k
0,b
0
>
>
>
<
<
<
<
<
=
=
归纳提炼:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
针对训练
x
O
D
x
O
C
y
x
O
B
已知函数
y
=
kx的图象在二、四象限,那么函数y
=
kx-k的图象可能是(
)
B
y
y
y
x
O
A
已知一次函数
y=(1-2m)x+(m-1)
,
求满足下列条件的m的值:
(1)函数值y
随x的增大而增大;
(2)函数图象与y
轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
挑战自我
说一说,通过今天的学习,你有什么收获,还有什么困惑,与同伴交流一下!
课堂小结
一次函数函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是(
,0),
当k>0,
b>0时,经过一、二、三象限;
当k>0
,b<0时,经过一、三、四象限;
当k<0
,b>0时,经过
一、二、四象限;
当k<0
,b<0时,经过二、三、四象限.
图象
性质
1.
一次函数y=x-2的大致图象为(
)
C
A
B
C
D
作业检测
4.直线y
=2x-3
与x
轴交点的坐标为________;与y
轴交点的坐标为________;图象经过____________象限,
y
随x
的增大而________.
2.下列函数中,y的值随x值的增大而增大的函数是(
).
A.y=-2x
B.y=-2x+1
C.y=x-2
D.y=-x-2
C
3.直线y=3x-2可由直线y=3x向
平移
单位得到.
下
2
6.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1
y2(填“>”或“<”).
>
(0,-3)
一、三、四
增大
(1.5,0)
5.若直线y=kx+2与y=3x-1平行,则k=
.
3
7.已知一次函数y=(3m-8)x+(1-m)图象与
y轴交点在x轴下方,且y随x的增大而减小,其中m为整数,求m的值
.
解:
由题意得
,解得
又∵m为整数,
∴m=2
课堂小结
一次函数函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是(
,0),
当k>0,
b>0时,经过一、二、三象限;
当k>0
,b<0时,经过一、三、四象限;
当k<0
,b>0时,经过
一、二、四象限;
当k<0
,b<0时,经过二、三、四象限.
图象
性质
19.2.2.2一次函数的图象与性质
一、知识链接
形如
的函数,叫做一次函数;
3.正比例函数的图象是一条经过
点的
.
y=kx+b(k,b是常数,k≠0)
原
直线
2.画函数图象的步骤有
,
,
.
列表
描点
连线
(写解析式)
1.
什么是一次函数?
自主学习
正比例函数
解析式
y
=kx(k≠0)
性质:k>0,y
随x
的增大而增大;k<0,y
随
x
的增大而减小.
一次函数
解析式
y
=kx+b(k≠0)
类比正比例函数
y
=kx(k≠0),研究一次函数
y
=kx+b(k≠0)的图象和性质。
图象:经过原点和
(1,k)的一条直线
x
y
O
k>0
k<0
x
y
O
?
?
二、新知预习
1.在如图所示的平面直角坐标系中画出一次函数y2=-6x+5
及正比例函数y1
=-6x的图象.
2.观察画出的函数图象回答问题:
(1)这两个函数的图象形状是
,并且倾斜程度
.
(2)函数y1=-6x的图象经过
点,
函数y2=
-6x+5的图像与y轴交于点
,即它可以看作由直线y1
=-6x
向
平移
个单位长度而得到.
函数y2=
-6x+5的图象经过第
象限,且y随x的增大而
.
一条直线
相同
原
(0,5)
上
5
减小
3.自主归纳:
(1)当k>0时,y随x的增大而
,当k<0时,y随x的增大而
.
(2)一次函数y=kx+b的图象可以由正比例函数y=kx的图象沿y轴方向平移
个单位长度得到(当b>0时,
向
平移;当b<0时,向
平移).
增大
减小
上
下
三、自学自测
1.与一次函数y=2x-3的图象平行的是下列哪个函数的图象(
)
A.y=-x-3
B.y=2x+1
C.y=-2x
D.y=3x+3
2.下列一次函数中,y随x值的增大而减小的是(
)
A.
y=2x+1
B.
y=-4x+3
C.y=x+2
D.
y=(5-2)x
B
B
O
例1
用你认为最简单的方法画出下列函数的图象:
(1)
y=-2x-1;(2)
y=0.5x+1
x
0
1
y=-2x-1
y=0.5x+1
-1
-3
1
y=-2x-1
1.5
y=0.5x+1
方法总结:
由于两点确定一条直线,画一次函数
y
=kx+b(k≠0)图象时我们只需描点(0,
)和点(
,0)过以上两点作直线即可.
b
一次函数的性质
二
例2
在同一坐标系中画出下列一次函数的图象:
(1)y1
=x+2;
(2)y2
=2x-1;
(3)y3
=-x+2; (4)y4
=-2x-2.
思考:仿照正比例函数的做法,你能看出当
k
的符号
变化时,函数的增减性怎样变化吗?
要点归纳:
(1)当k>0时,图象从左到右呈
趋势,y随自变量x的增大而
;
①b>0时,直线经过第
象限;
②
b<0时,直线经过第
象限.
(2)当k<0时,图象从左到右呈
趋势,y随自变量x的增大而
.
①b>0时,直线经过第
象限;
②
b<0时,直线经过第
象限.
上升
增大
三、二、一
三、四、一
下降
减小
二、一、四
二、三、四
O
y1
=x+2
y2
=2x-1
O
y3=-x+2
y4
=-2x-2
五、合作提升
一次函数y=kx+b(k≠0)
图象
画一次函数图象时我们只需描点(0,b)和点(
,0)连线即可.(两点法)
k>0
k<0
b>0
b=0
b<0
b>0
b=0
b<0
图象是自左向右呈
趋势
图象是自左向右呈
趋势
经过第
象限
经过第
象限
经过第
象限
经过第
象限
经过第
象限
经过第
象限
|k|越大,图象越陡(即越靠近y轴)
性质
y随x的增大而
.
y随x的增大而
.
图象平移
一次函数y=kx+b(k≠0)的图象可以由正比例函数y=kx的图象沿y轴方向平移
个单位长度得到(当b>0时,向
平移;当b<0时,向
平移)
根据一次函数的图象判断k,b的正负,并说出直线经过的象限
k
0,b
0
>
>
k
0,b
0
k
0,b
0
k
0,b
0
k
0,b
0
k
0,b
0
>
>
>
<
<
<
<
<
=
=
归纳提炼:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
针对训练
x
O
D
x
O
C
y
x
O
B
已知函数
y
=
kx的图象在二、四象限,那么函数y
=
kx-k的图象可能是(
)
B
y
y
y
x
O
A
已知一次函数
y=(1-2m)x+(m-1)
,
求满足下列条件的m的值:
(1)函数值y
随x的增大而增大;
(2)函数图象与y
轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
挑战自我
说一说,通过今天的学习,你有什么收获,还有什么困惑,与同伴交流一下!
课堂小结
一次函数函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是(
,0),
当k>0,
b>0时,经过一、二、三象限;
当k>0
,b<0时,经过一、三、四象限;
当k<0
,b>0时,经过
一、二、四象限;
当k<0
,b<0时,经过二、三、四象限.
图象
性质
1.
一次函数y=x-2的大致图象为(
)
C
A
B
C
D
作业检测
4.直线y
=2x-3
与x
轴交点的坐标为________;与y
轴交点的坐标为________;图象经过____________象限,
y
随x
的增大而________.
2.下列函数中,y的值随x值的增大而增大的函数是(
).
A.y=-2x
B.y=-2x+1
C.y=x-2
D.y=-x-2
C
3.直线y=3x-2可由直线y=3x向
平移
单位得到.
下
2
6.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,则y1
y2(填“>”或“<”).
>
(0,-3)
一、三、四
增大
(1.5,0)
5.若直线y=kx+2与y=3x-1平行,则k=
.
3
7.已知一次函数y=(3m-8)x+(1-m)图象与
y轴交点在x轴下方,且y随x的增大而减小,其中m为整数,求m的值
.
解:
由题意得
,解得
又∵m为整数,
∴m=2
课堂小结
一次函数函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是(
,0),
当k>0,
b>0时,经过一、二、三象限;
当k>0
,b<0时,经过一、三、四象限;
当k<0
,b>0时,经过
一、二、四象限;
当k<0
,b<0时,经过二、三、四象限.
图象
性质
