五年级数学下册课件 4.4.1 最大公因数的应用 人教版(共13张PPT)
文档属性
| 名称 | 五年级数学下册课件 4.4.1 最大公因数的应用 人教版(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 17.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 21:15:19 | ||
图片预览

文档简介
(共13张PPT)
最大公因数的应用
例3
人教版五年级下册第四单元
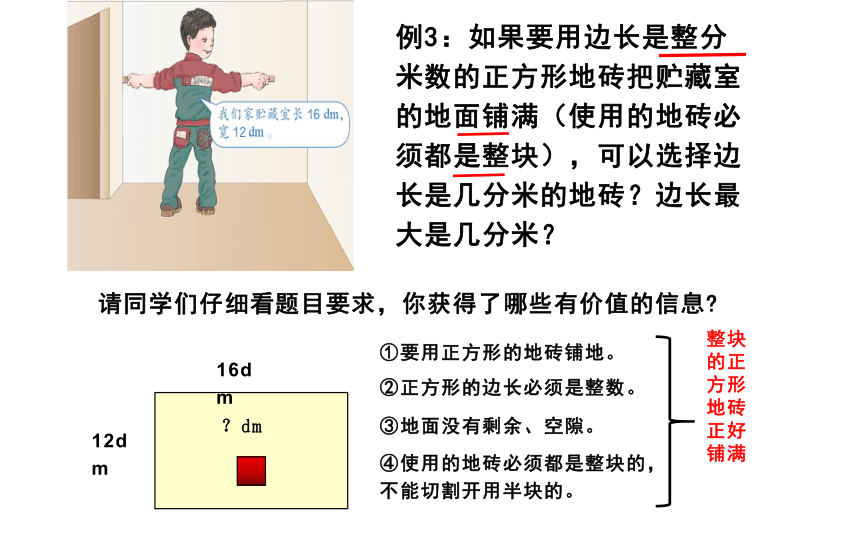
例3:如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块),可以选择边长是几分米的地砖?边长最大是几分米?
16dm
12dm
请同学们仔细看题目要求,你获得了哪些有价值的信息?
①要用正方形的地砖铺地。
③地面没有剩余、空隙。
②正方形的边长必须是整数。
④使用的地砖必须都是整块的,不能切割开用半块的。
整块的正方形地砖正好铺满
?dm
16dm
12dm
?dm
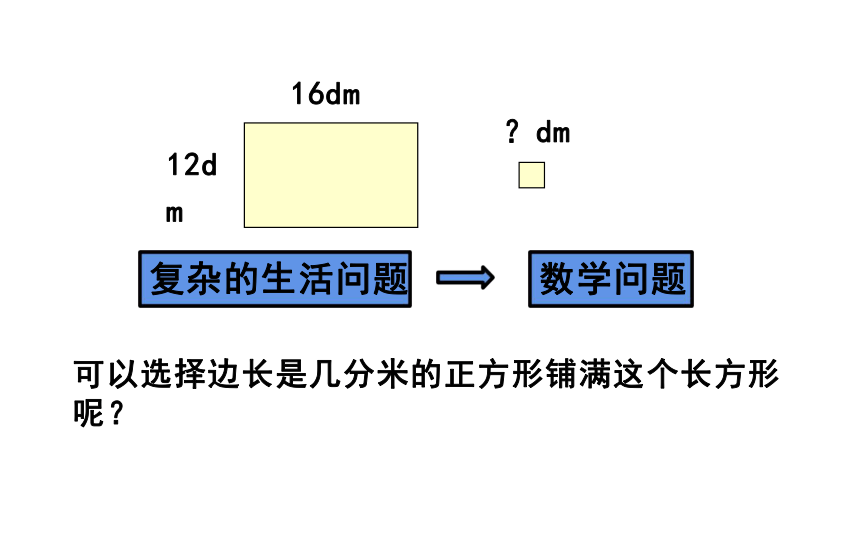
复杂的生活问题
数学问题
可以选择边长是几分米的正方形铺满这个长方形呢?
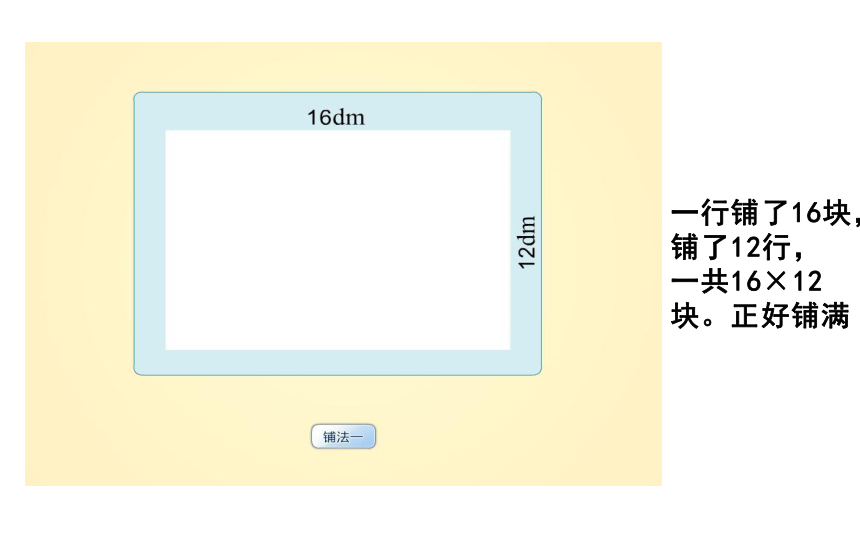
一行铺了16块,
铺了12行,
一共16×12块。正好铺满
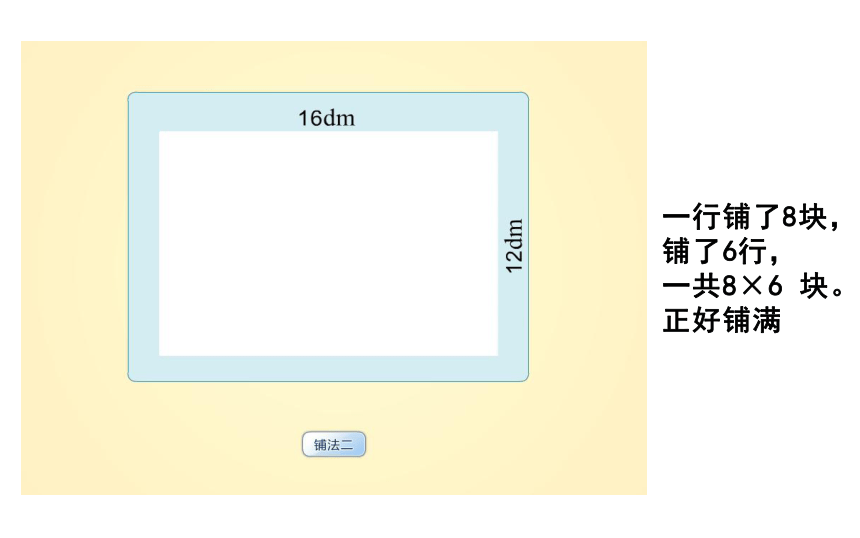
一行铺了8块,
铺了6行,
一共8×6
块。正好铺满
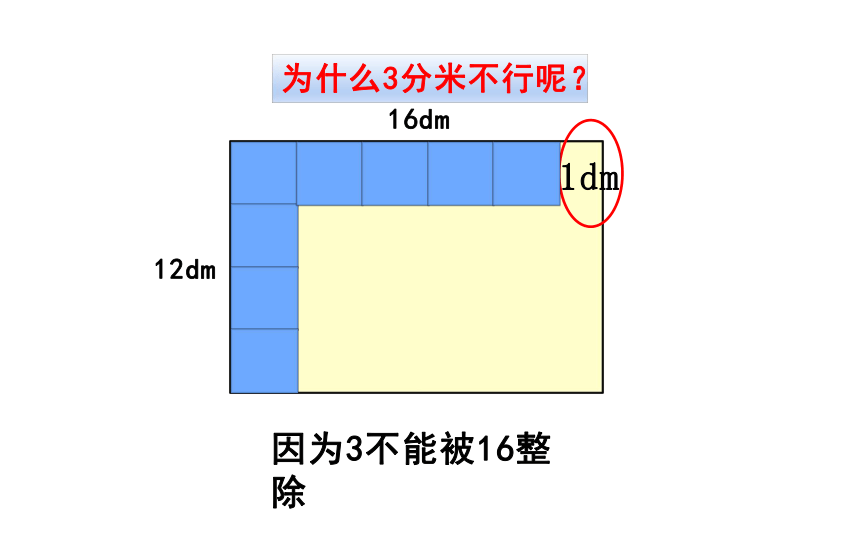
为什么3分米不行呢?
16dm
12dm
因为3不能被16整除
1dm
一行铺了4块,
铺了3行,
一共4×3
块。正好铺满
为什么5分米不行呢?
16dm
12dm
2dm
1dm
因为5既不能被16整除,也不能被12整除
在铺的过程中不需要全部铺完,只需要铺出一行和一列就可以了。
16dm
12dm
?dm
整数块正好铺满的正方形的边长既能被长整除,又能被宽整除。
也就是长和宽的公因数
边长最大是长和宽的最大公因数
16的因数:
1,2,4,8,16
12的因数:
1,2,3,4,6,12
12与16的公因数:1
、2
、4
最大公因数:4
。
答:可以选择边长是1分米、2分米、4分米的正方形地砖;
边长最大是4分米。
规范做题格式
1.
有一张长方形纸,长
70
cm,宽
50
cm。如果要
剪成若干同样大小的正方形而没有剩余,剪出的正方形的边长最大是几厘米?
2.老师买来水果糖36个和棒棒糖24个分别平均分给一个组的同学,都正好分完。这个组最多可能有几位同学?
公因数
最大公因数
通过分析题目发现,这类问题一般在条件中会出现没有剩余、数量相同、正好分完等字眼;在问题中会出现最大、最多、最长等字眼。
具体问题具体分析
解决此类问题的方法就是求已知量间的公因数和最大公因数。
问题特点总结
最大公因数的应用
例3
人教版五年级下册第四单元
例3:如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块),可以选择边长是几分米的地砖?边长最大是几分米?
16dm
12dm
请同学们仔细看题目要求,你获得了哪些有价值的信息?
①要用正方形的地砖铺地。
③地面没有剩余、空隙。
②正方形的边长必须是整数。
④使用的地砖必须都是整块的,不能切割开用半块的。
整块的正方形地砖正好铺满
?dm
16dm
12dm
?dm
复杂的生活问题
数学问题
可以选择边长是几分米的正方形铺满这个长方形呢?
一行铺了16块,
铺了12行,
一共16×12块。正好铺满
一行铺了8块,
铺了6行,
一共8×6
块。正好铺满
为什么3分米不行呢?
16dm
12dm
因为3不能被16整除
1dm
一行铺了4块,
铺了3行,
一共4×3
块。正好铺满
为什么5分米不行呢?
16dm
12dm
2dm
1dm
因为5既不能被16整除,也不能被12整除
在铺的过程中不需要全部铺完,只需要铺出一行和一列就可以了。
16dm
12dm
?dm
整数块正好铺满的正方形的边长既能被长整除,又能被宽整除。
也就是长和宽的公因数
边长最大是长和宽的最大公因数
16的因数:
1,2,4,8,16
12的因数:
1,2,3,4,6,12
12与16的公因数:1
、2
、4
最大公因数:4
。
答:可以选择边长是1分米、2分米、4分米的正方形地砖;
边长最大是4分米。
规范做题格式
1.
有一张长方形纸,长
70
cm,宽
50
cm。如果要
剪成若干同样大小的正方形而没有剩余,剪出的正方形的边长最大是几厘米?
2.老师买来水果糖36个和棒棒糖24个分别平均分给一个组的同学,都正好分完。这个组最多可能有几位同学?
公因数
最大公因数
通过分析题目发现,这类问题一般在条件中会出现没有剩余、数量相同、正好分完等字眼;在问题中会出现最大、最多、最长等字眼。
具体问题具体分析
解决此类问题的方法就是求已知量间的公因数和最大公因数。
问题特点总结
