2020—2021学年人教版数学七年级下册课件-6.3 实数——为什么√2不是有理数(18张)
文档属性
| 名称 | 2020—2021学年人教版数学七年级下册课件-6.3 实数——为什么√2不是有理数(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 19:19:26 | ||
图片预览






文档简介
(共18张PPT)
复习
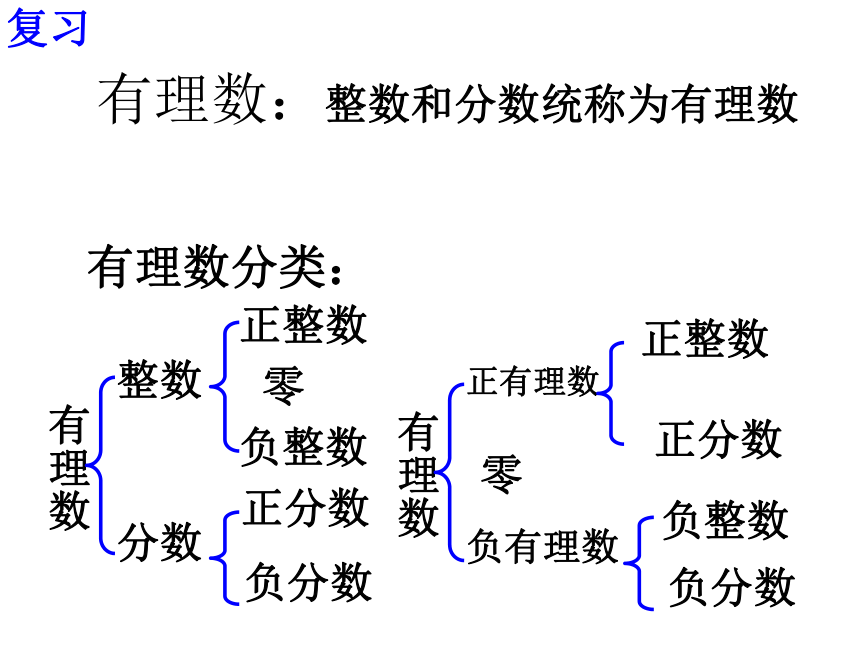
有理数分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
负有理数
正整数
零
负整数
正分数
负分数
有理数:
整数和分数统称为有理数
把下列各有理数写成小数的形式:
有限小数
无限循环小数
任何一个有理数都可写成有限小数和无限循环小数的形式.
探究新知
1.2
.
0.81
. .
0.5
.
小组合作
任何一个有限小数和无限循环小数都能化为分数吗?
0.7
.
0.14
.
.
有限小数和无限循环小数都是有理数
0.34
探究
把下列各数写成小数的形式:
无限不循环小数
有理数和无理数统称为实数
无理数的概念:无限不循环小数叫无理数.
1.4142…
1.442…
1.7320 …
1.710…
2.236…
1.913…
3.14159265…
1.圆周率 及化简后含有 的数
2.开方开不尽数的方根
3.特殊结构的数
常见的无理数的形式:
注意:带根号的数不一定是无理数
你知道怎样区分有理数和无理数吗?
无限不循环小数
通过计算器计算得
反证法是一种间接证法,它是先提出一个与命题的结论相反的假设,然后,从这个假设出发,经过正确的推理,导致矛盾,从而否定相反的假设,达到肯定原命题正确的一种方法。
用反证法证明一个命题的步骤,大体上分为:(1)反设;(2)归谬;(3)结论。
反证法
那么存在两个互质的正整数p,q,使得
于是
两边平方得
由于2q 是偶数,可得p 是偶数,而只有偶数的平方才是偶数,
所以p也是偶数.
因此可设p=2s,代入上式,得4s =2q ,即
q =2s .
所以q也是偶数.这样,p和q都是偶数,不互质,这与假设p,q互质矛盾.
这个矛盾说明,
不能写成分数的形式,
注意
事实上,无理数只是一种命名,并非“无理”,而是实际存在的不能写成分数形式的数,它和有理数一样,都是现实世界中客观存在的量的反映。
探究新知
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示 的点吗?
能否用两个面积为1的小正方形拼成一个面积为2的大正方形?
设大正方形的边长为x
则 x2 = 2
x =
大正方形的边长
是多少?
动手操作
以一个单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点表示什么?
-2 -1 0 1 2
无理数 可以用数轴上的点表示
归纳
0 1 2 3 4
1、每一个有理数都可以用数轴上的点
表示;
2、每一个无理数都可以用数轴上的点
表示;
每一个实数都可用数轴上的点来表示;
即实数与数轴上的点是一一对应的
数轴上的每一个点都表示一个实数;
学以致用
判断正误,并说明理由.
(1)无理数都是无限小数;( )
(2) 实数包括正实数、0、负实数;( )
(3)不带根号的数都是有理数;( )
(4)所有有理数都可以用数轴上的点表示, 反过来,数轴上所有的点都表示有理数.( )
5)数轴上的任何一点都可以表示实数。( )
×
×
(
运用新知
1. 下列各数中,哪些是有理数?哪些是无理数?
2、下列各数中,不是无理数的是( )
A.π B. C. D.
说说本节课的收获
作业
复习
有理数分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
负有理数
正整数
零
负整数
正分数
负分数
有理数:
整数和分数统称为有理数
把下列各有理数写成小数的形式:
有限小数
无限循环小数
任何一个有理数都可写成有限小数和无限循环小数的形式.
探究新知
1.2
.
0.81
. .
0.5
.
小组合作
任何一个有限小数和无限循环小数都能化为分数吗?
0.7
.
0.14
.
.
有限小数和无限循环小数都是有理数
0.34
探究
把下列各数写成小数的形式:
无限不循环小数
有理数和无理数统称为实数
无理数的概念:无限不循环小数叫无理数.
1.4142…
1.442…
1.7320 …
1.710…
2.236…
1.913…
3.14159265…
1.圆周率 及化简后含有 的数
2.开方开不尽数的方根
3.特殊结构的数
常见的无理数的形式:
注意:带根号的数不一定是无理数
你知道怎样区分有理数和无理数吗?
无限不循环小数
通过计算器计算得
反证法是一种间接证法,它是先提出一个与命题的结论相反的假设,然后,从这个假设出发,经过正确的推理,导致矛盾,从而否定相反的假设,达到肯定原命题正确的一种方法。
用反证法证明一个命题的步骤,大体上分为:(1)反设;(2)归谬;(3)结论。
反证法
那么存在两个互质的正整数p,q,使得
于是
两边平方得
由于2q 是偶数,可得p 是偶数,而只有偶数的平方才是偶数,
所以p也是偶数.
因此可设p=2s,代入上式,得4s =2q ,即
q =2s .
所以q也是偶数.这样,p和q都是偶数,不互质,这与假设p,q互质矛盾.
这个矛盾说明,
不能写成分数的形式,
注意
事实上,无理数只是一种命名,并非“无理”,而是实际存在的不能写成分数形式的数,它和有理数一样,都是现实世界中客观存在的量的反映。
探究新知
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示 的点吗?
能否用两个面积为1的小正方形拼成一个面积为2的大正方形?
设大正方形的边长为x
则 x2 = 2
x =
大正方形的边长
是多少?
动手操作
以一个单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点表示什么?
-2 -1 0 1 2
无理数 可以用数轴上的点表示
归纳
0 1 2 3 4
1、每一个有理数都可以用数轴上的点
表示;
2、每一个无理数都可以用数轴上的点
表示;
每一个实数都可用数轴上的点来表示;
即实数与数轴上的点是一一对应的
数轴上的每一个点都表示一个实数;
学以致用
判断正误,并说明理由.
(1)无理数都是无限小数;( )
(2) 实数包括正实数、0、负实数;( )
(3)不带根号的数都是有理数;( )
(4)所有有理数都可以用数轴上的点表示, 反过来,数轴上所有的点都表示有理数.( )
5)数轴上的任何一点都可以表示实数。( )
×
×
(
运用新知
1. 下列各数中,哪些是有理数?哪些是无理数?
2、下列各数中,不是无理数的是( )
A.π B. C. D.
说说本节课的收获
作业
