2020-2021学年苏科版数学八年级下册 第11章 反比例函数的图象和性质 能力提优训练(word版无答案)
文档属性
| 名称 | 2020-2021学年苏科版数学八年级下册 第11章 反比例函数的图象和性质 能力提优训练(word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 626.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览

文档简介
八下数学《反比例函数的图象和性质》能力提优训练
知识点:1.反比例函数的图象是双曲线;2.反比例函数y
=
的性质:(1)当k
>
0时,双曲线的两支分别位于第一、三象限,在每个象限内,y随x的增大而减小;(2)当k
<
0时,双曲线的两支分别位于第二、四象限,在每个象限内,y随x的增大而增大.
1.已知反比例函数的图象位于第二、四象限,则k的取值范围是
_________
.已知反比例函数
,当x
>
0时,y随x的增大而增大,则k的取值是
_________
.
2.已知点都在反比例函数的图象上,则的大小关系是
_________
(用“
<
”连接).
3.已知点都在反比例函数的图象上,则的大小关系是
_________
(用“
<
”连接).
4.已知点M(3,-4)在反比例函数的图象上,当1
<
x
<
5时,y的取值范围是
_________
.
5.已知反比例函数的图象上有两点,且,则k的取值范围是
_________
.
6.已知点A(2,3)在反比例函数的图象上,点也在该反比例函数的图象上,且,则与的大小关系是
_________
.
7.已知点在双曲线y
=
(k
>
0)上,若,则a的取值范围是
_________
.
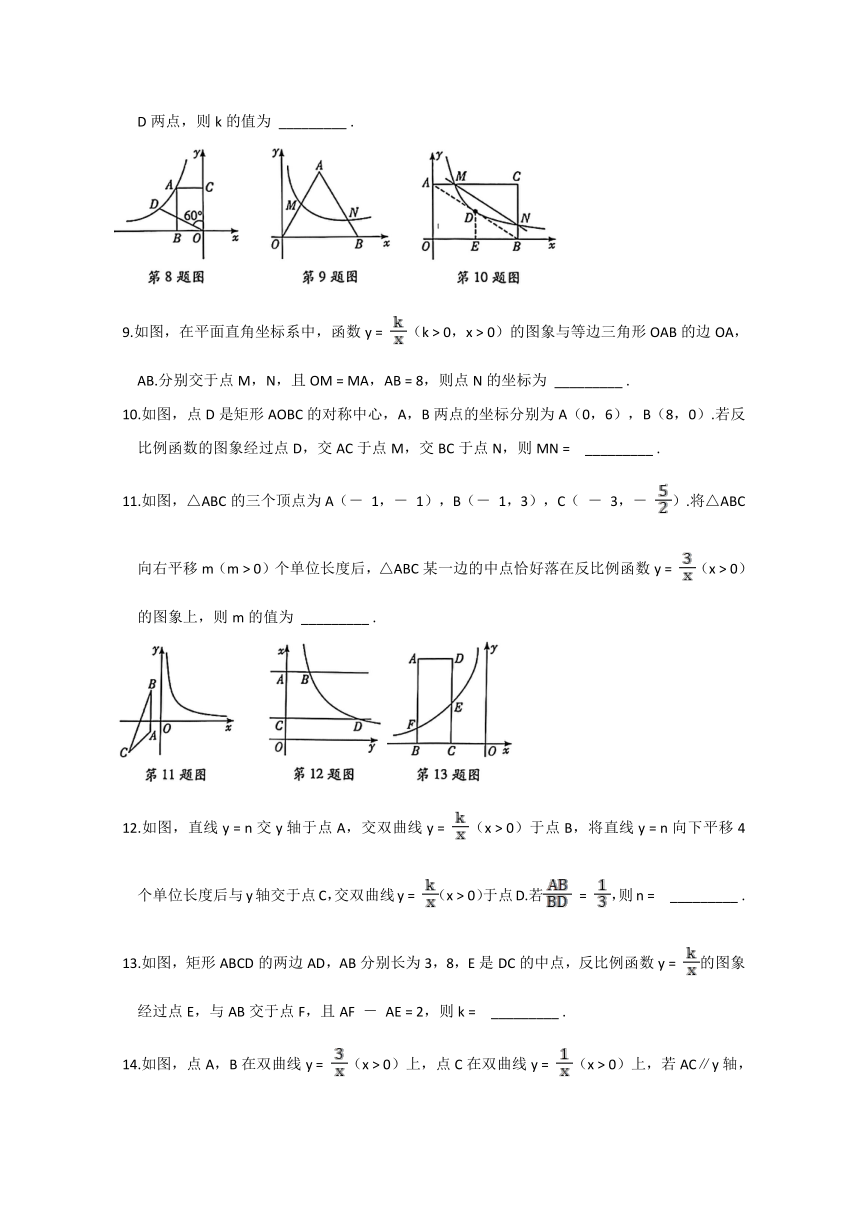
8.如图,矩形ABOC的顶点B,C分别在x轴,y轴上,顶点A在第二象限,点B的坐标为(-2,0).将线段OC绕点O逆时针旋转60°至线段OD.若反比例函数y
=
(k≠0)的图象经过A,D两点,则k的值为
_________
.
9.如图,在平面直角坐标系中,函数y
=
(k
>
0,x
>
0)的图象与等边三角形OAB的边OA,AB.分别交于点M,N,且OM
=
MA,AB
=
8,则点N的坐标为
_________
.
10.如图,点D是矩形AOBC的对称中心,A,B两点的坐标分别为A(0,6),B(8,0).若反比例函数的图象经过点D,交AC于点M,交BC于点N,则MN
=
_________
.
11.如图,△ABC的三个顶点为A(-
1,-
1),B(-
1,3),C(
-
3,-
).将△ABC向右平移m(m
>
0)个单位长度后,△ABC某一边的中点恰好落在反比例函数y
=
(x
>
0)的图象上,则m的值为
_________
.
12.如图,直线y
=
n交y轴于点A,交双曲线y
=
(x
>
0)于点B,将直线y
=
n向下平移4个单位长度后与y轴交于点C,交双曲线y
=
(x
>
0)于点D.若
=
,则n
=
_________
.
13.如图,矩形ABCD的两边AD,AB分别长为3,8,E是DC的中点,反比例函数y
=
的图象经过点E,与AB交于点F,且AF
-
AE
=
2,则k
=
_________
.
14.如图,点A,B在双曲线y
=
(x
>
0)上,点C在双曲线y
=
(x
>
0)上,若AC∥y轴,BC∥x轴,且AC
=
BC,则AB
=
_________
.
15.如图,在平面直角坐标系中,已知A(0,18),(6,0),点B在第一象限内,且四边形ABCO是矩形,动点P从点A出发,以每秒4个单位长度的速度向点O运动,直到点O为止;动点Q同时从点C出发,以每秒2个单位长度的速度向点B运动,与点P同时结束运动.连接AC,与PQ相交于点D,若双曲线y
=
过点D,则k
=
_________
.
16.如图,△AOB为等边三角形,点B的坐标为(-
2,0),过点C(2,0)作直线交AO于点D,交AB于点E,点E在反比例函数y
=
的图象上.当△ADE和△DCO的面积相等时,k
=
_________
.
17.如图,点A,D在x轴正半轴上,点C在y轴正半轴上,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y
=
(x
>
0)的图象上,则点E的坐标是
_________
.
18.如图,是反比例函数y
=
(k
>
0)在第一象限图象上的一点,点的坐标为(2,0).若△P1OA1与△P2A1A2均为等边三角形,则点A2的横坐标为
_________
.
19.如图,A,B两点在反比例函数的图象上,C,D两点在反比例函数的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC
=
2,BD
=
4,EF
=
3,则=
_________
.
20.如图,A(1,a),P是双曲线y
=
上两点,∠POA
=
45°,求点P的坐标.
21.如图,已知点A(0,-
3),点B(2,0),将线段AB平移至DC的位置,点D在x轴的负半轴上,点C在反比例函数y
=
的图象上.若S△BCD
=
9,求k的值.
22.在平面直角坐标系中,已知点A(-
6,0),点D(-
7,3),点B,C在第二象限内,且四边形ABCD是正方形.
(1)求B,C两点的坐标;
(2)将正方形ABCD以每秒1个单位长度的速度沿x轴向右平移t秒,在平移过程中,点A,B,C,D分别对应点A′,B′,C′,D′,当点B′,D′正好落在反比例函数y
=
(x
>
0)的图象上时,求t和k的值;
(3)在(2)的条件下,点P在x轴上,点Q在反比例函数y
=
的图象上,若以P,Q,B′,D′四点为顶点的四边形是平行四边形,求点P,Q的坐标.
23.如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的对称中心P在反比例函数y
=
(k
>
0,x
>
0)的图象上,边CD在x轴上,点B在y轴上.
(1)点A是否在该反比例函数的图象上?请说明理由;
(2)若该反比例函数的图象与DE交于点Q,求点Q的坐标;
(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程
24.如图,在平面直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y
=
的图象上.
(1)求反比例函数的表达式;
(2)把△OAB向右平移a(a
>
0)个单位长度,对应得到△O′A′B′,当这个反比例函数的图象经过△O′A′B′一边的中点时,求a的值.
知识点:1.反比例函数的图象是双曲线;2.反比例函数y
=
的性质:(1)当k
>
0时,双曲线的两支分别位于第一、三象限,在每个象限内,y随x的增大而减小;(2)当k
<
0时,双曲线的两支分别位于第二、四象限,在每个象限内,y随x的增大而增大.
1.已知反比例函数的图象位于第二、四象限,则k的取值范围是
_________
.已知反比例函数
,当x
>
0时,y随x的增大而增大,则k的取值是
_________
.
2.已知点都在反比例函数的图象上,则的大小关系是
_________
(用“
<
”连接).
3.已知点都在反比例函数的图象上,则的大小关系是
_________
(用“
<
”连接).
4.已知点M(3,-4)在反比例函数的图象上,当1
<
x
<
5时,y的取值范围是
_________
.
5.已知反比例函数的图象上有两点,且,则k的取值范围是
_________
.
6.已知点A(2,3)在反比例函数的图象上,点也在该反比例函数的图象上,且,则与的大小关系是
_________
.
7.已知点在双曲线y
=
(k
>
0)上,若,则a的取值范围是
_________
.
8.如图,矩形ABOC的顶点B,C分别在x轴,y轴上,顶点A在第二象限,点B的坐标为(-2,0).将线段OC绕点O逆时针旋转60°至线段OD.若反比例函数y
=
(k≠0)的图象经过A,D两点,则k的值为
_________
.
9.如图,在平面直角坐标系中,函数y
=
(k
>
0,x
>
0)的图象与等边三角形OAB的边OA,AB.分别交于点M,N,且OM
=
MA,AB
=
8,则点N的坐标为
_________
.
10.如图,点D是矩形AOBC的对称中心,A,B两点的坐标分别为A(0,6),B(8,0).若反比例函数的图象经过点D,交AC于点M,交BC于点N,则MN
=
_________
.
11.如图,△ABC的三个顶点为A(-
1,-
1),B(-
1,3),C(
-
3,-
).将△ABC向右平移m(m
>
0)个单位长度后,△ABC某一边的中点恰好落在反比例函数y
=
(x
>
0)的图象上,则m的值为
_________
.
12.如图,直线y
=
n交y轴于点A,交双曲线y
=
(x
>
0)于点B,将直线y
=
n向下平移4个单位长度后与y轴交于点C,交双曲线y
=
(x
>
0)于点D.若
=
,则n
=
_________
.
13.如图,矩形ABCD的两边AD,AB分别长为3,8,E是DC的中点,反比例函数y
=
的图象经过点E,与AB交于点F,且AF
-
AE
=
2,则k
=
_________
.
14.如图,点A,B在双曲线y
=
(x
>
0)上,点C在双曲线y
=
(x
>
0)上,若AC∥y轴,BC∥x轴,且AC
=
BC,则AB
=
_________
.
15.如图,在平面直角坐标系中,已知A(0,18),(6,0),点B在第一象限内,且四边形ABCO是矩形,动点P从点A出发,以每秒4个单位长度的速度向点O运动,直到点O为止;动点Q同时从点C出发,以每秒2个单位长度的速度向点B运动,与点P同时结束运动.连接AC,与PQ相交于点D,若双曲线y
=
过点D,则k
=
_________
.
16.如图,△AOB为等边三角形,点B的坐标为(-
2,0),过点C(2,0)作直线交AO于点D,交AB于点E,点E在反比例函数y
=
的图象上.当△ADE和△DCO的面积相等时,k
=
_________
.
17.如图,点A,D在x轴正半轴上,点C在y轴正半轴上,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y
=
(x
>
0)的图象上,则点E的坐标是
_________
.
18.如图,是反比例函数y
=
(k
>
0)在第一象限图象上的一点,点的坐标为(2,0).若△P1OA1与△P2A1A2均为等边三角形,则点A2的横坐标为
_________
.
19.如图,A,B两点在反比例函数的图象上,C,D两点在反比例函数的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC
=
2,BD
=
4,EF
=
3,则=
_________
.
20.如图,A(1,a),P是双曲线y
=
上两点,∠POA
=
45°,求点P的坐标.
21.如图,已知点A(0,-
3),点B(2,0),将线段AB平移至DC的位置,点D在x轴的负半轴上,点C在反比例函数y
=
的图象上.若S△BCD
=
9,求k的值.
22.在平面直角坐标系中,已知点A(-
6,0),点D(-
7,3),点B,C在第二象限内,且四边形ABCD是正方形.
(1)求B,C两点的坐标;
(2)将正方形ABCD以每秒1个单位长度的速度沿x轴向右平移t秒,在平移过程中,点A,B,C,D分别对应点A′,B′,C′,D′,当点B′,D′正好落在反比例函数y
=
(x
>
0)的图象上时,求t和k的值;
(3)在(2)的条件下,点P在x轴上,点Q在反比例函数y
=
的图象上,若以P,Q,B′,D′四点为顶点的四边形是平行四边形,求点P,Q的坐标.
23.如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的对称中心P在反比例函数y
=
(k
>
0,x
>
0)的图象上,边CD在x轴上,点B在y轴上.
(1)点A是否在该反比例函数的图象上?请说明理由;
(2)若该反比例函数的图象与DE交于点Q,求点Q的坐标;
(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程
24.如图,在平面直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y
=
的图象上.
(1)求反比例函数的表达式;
(2)把△OAB向右平移a(a
>
0)个单位长度,对应得到△O′A′B′,当这个反比例函数的图象经过△O′A′B′一边的中点时,求a的值.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
