2021年苏科版八年级下册(压轴题培优练)专题02平行四边形B卷(word版含解析)
文档属性
| 名称 | 2021年苏科版八年级下册(压轴题培优练)专题02平行四边形B卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 611.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览




文档简介
2021年苏科版八年级下册(压轴题培优练)
专题02平行四边形B卷(解析版)
一、选择题(每小题只有一个选项是正确的,请将正确选项前的字母代号填写在括号内)
1.
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2020次,点B的落点依次为B1,B2,B3,…,则B2020的坐标为(
)
A.
(1345,0)
B.
(1345.5,)
C.
(1346,0)
D.
(1346.5,)
【答案】C
【解析】连接AC,如图所示.
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB=OA=1,
画出第5次、第6次、第7次翻转后的图形,如图所示.
由图可知:每翻转6次,图形向右平移4.
∵2020=336×6+4,
∴点B4向右平移1344(即336×4)到点B2020.
∵B4的坐标为(2,0),
∴B2020的坐标为(2+1344,0),
∴B2020的坐标为(1346,0).
故选:C.
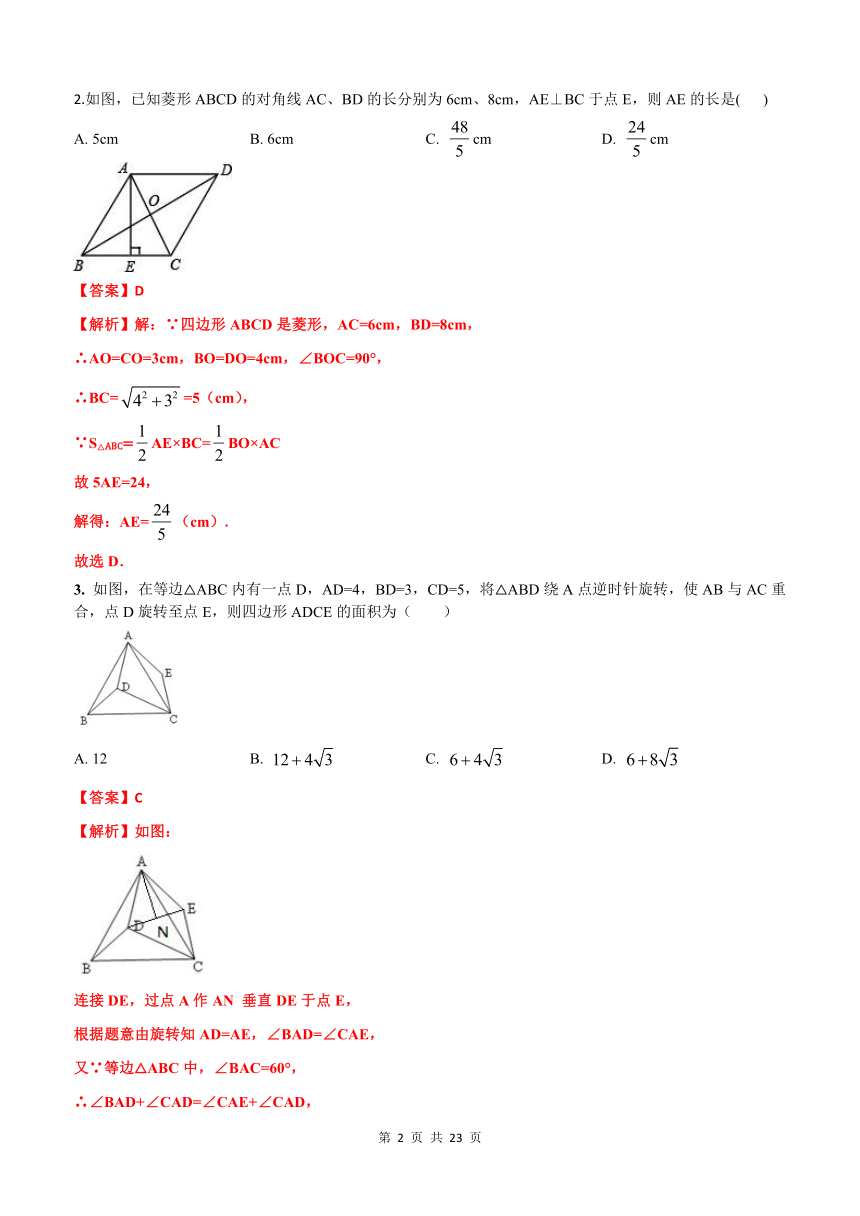
2.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是(
)
A.
5cm
B.
6cm
C.
cm
D.
cm
【答案】D
【解析】解:∵四边形ABCD是菱形,AC=6cm,BD=8cm,
∴AO=CO=3cm,BO=DO=4cm,∠BOC=90°,
∴BC==5(cm),
∵S△ABC=AE×BC=BO×AC
故5AE=24,
解得:AE=(cm).
故选D.
3.
如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为(
)
A.
12
B.
C.
D.
【答案】C
【解析】如图:
连接DE,过点A作AN
垂直DE于点E,
根据题意由旋转知AD=AE,∠BAD=∠CAE,
又∵等边△ABC中,∠BAC=60°,
∴∠BAD+∠CAD=∠CAE+∠CAD,
即∠BAC=∠DAE=60°,
∴△ADE是等边三角形,
∴DE=AD=4,
又BD=3,CD=5,
∴
,
∴△CDE是直角三角形,
∵AD=4,∠ADE=60°,
∴∠DAN=30°,
∴DN=2,
由勾股定理得AN=
,
∵=,
,
,
∴,
即四边形ADCE的面积是,
故答案为:C.
4.如图,菱形的对角线,交于点,,将沿点到点的方向平移,得到,当点与点重合时,点与点之间的距离为(
)
A.
B.
C.
D.
【答案】C
【解析】由菱形的性质得
为直角三角形
故选C
5.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=8,则四边形ABCD的面积为( )
A.
32
B.
24
C.
40
D.
36
【答案】A
【解析】解:如图,作AM⊥BC、AN⊥CD,交CD的延长线于点N;
∵∠BAD=∠BCD=90°
∴四边形AMCN为矩形,∠MAN=90°;
∵∠BAD=90°,
∴∠BAM=∠DAN;
在△ABM与△ADN中,
∴△ABM≌△ADN(AAS),
∴AM=AN(设为a);△ABM与△ADN的面积相等;
∴四边形ABCD的面积=正方形AMCN的面积;
由勾股定理得:AC2=AM2+MC2,而AC=8;
∴2a2=64,a2=32,
故选:A.
6.在平面直角坐标系xOy中,点A(4,3),点B为x轴正半轴上一点,将△AOB绕其一顶点旋转180°,连接其余四个顶点得到一个四边形,若该四边形是一个轴对称图形,则满足条件的点有(
)
A.5个
B.4个
C.3个
D.2个
【答案】A.
7.
如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,
连接CE,△DEC的周长为(
)
A.10
B.11
C.12
D.13
【答案】A
8.如图,已知点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是(
)
A.
AB=CD
B.
AC=BD
C.
AC⊥BD
D.
AD=BC
【答案】A
【解析】解:∵点E、F、G、H分别是任意四边形ABCD中AD、BC、BD、AC的中点,∴EG=FH=AB,EH=FG=CD,
∵当EG=FH=
EH=FG时,四边形EGFH是菱形,
∴当AB=CD时,四边形EFGH是菱形.
故选:A.
二、填空题(不需写出解答过程,只需把答案直接填写在对应横线上)
9.如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点.当四边形ABCD满足_____
时,四边形EGFH是菱形.
【解析】本题可根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF,EG=HF,因此四边形EHFG是平行四边形,本题考查了菱形的判定,运用的是菱形的定义:一组邻边相等的平行四边形是菱形
【解答】证明:∵点E,G分别是AD,BD的中点,
∴EG∥AB,同理HF∥AB,∴EG∥HF,EG=HF=
∴四边形EGFH是平行四边形.
∵AB=CD,∴EG=EH,
∴四边形EGFH是菱形.
故答案为AB=CD.
10.已知:如图,AD、CE分别是△ABC的角平分线和中线,AD⊥CE,AD=CE=4,则BC的长等于
.
【答案】
【解析】如下图,过点B作CE垂线,交CE延长线于点F,AD与CE交于点H.
∵AD⊥EC,AD是∠EAC的角平分线
∴∠EAH=∠HAC
∴∠AEH=∠ACH,∴AE=AC,△AEC是等腰三角形
∵CE=4
∴EH=HC=2
∵CE是△ABC的中线,∴AE=EB
∵∠AEH=∠FEB,∠AHE=∠BFE=90°
∴△AEH≌△BEF
∴EF=2,FC=2+2+2=6,BF=AH
∵∠DCH=∠BCF,∠DHC=∠BFC=90°
∴△DCH∽△BCF
∴
∴3DH=BF,∴3DH=HA
∵AD=4
∴HD=1,FB=3
∴在Rt△CBF中,CB=
故答案为:
11.如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB,G、H是BC边上的点,且GH=BC,若,则=
.
【答案】2
【解析】解:连接AC、BD,如图,
∵点O是?ABCD的对称中心,
∴AC、BD交于点O,
∴S△AOB=S△BOC,
∵EF=AB,
∴S△EOF=S△AOB,
∵GH=BC,
∴S△OGH=S△BOC,
∴S△EOF:S△OGH=3:2,
∵,
∴=2.
故答案为:2.
12.如图,矩形ABCD的对角线交于点O,点E在线段AO上,且DE=DC,若∠EDO=15°,则∠DEC=______°.
【答案】55
【解析】解:设∠DEC=x,
∵DE=DC,
∴∠DCE=x,
∵四边形ABCD为矩形,
∴∠ODC=∠DCE=x,
∴∠DOE=∠OCD+∠ODC=2x,
∵△DOE内角和为180°,
∴,
解得:,
即∠DEC=,
故答案为:55.
13.
E、F是线段AB上的两点,且AB=16,AE=1,BF=3,点G是线段EF上的一动点,分别以AG、BG为斜边在AB同侧作两个等腰直角三角形,直角顶点分别为D、C,如图所示,连接CD并取中点P,连结PG,点G从E点出发运动到F点,则线段PG扫过的图形面积为______.
【答案】36
【解析】解:分别延长AD、BC交于点H,连接PH,EH,FH,
∵△ADG、△GCB为等腰直角三角形,
∴∠DGA=∠CGB=45°,
∴∠DGC=90°,
∴AH∥GC,
又∵∠HCG=90°,
∴∠HCG=∠DGC=90°,
∴DG∥HB,
∴四边形DGCH为矩形,
∵点P未DC中点,
∴点G、P、H三点共线,且P为HG的中点,
过P作MN∥于AB分别交EH、FH与M、N,
∴MN为△HEF的中位线,且MN即为点P的运动轨迹,
∴GP扫过的图形即为梯形MEFN,
∵AB=16,AE=1,BF=3,
∴EF=16-1-3=12,
∴,
过点H作HO垂直AB于O,
∴,
∴梯形的高为:,
∴,
即线段PG扫过的图形面积为36,
故答案为:36.
14.如图,在矩形ABCD中,AB=2,BC=,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则当OC为最大值时,点C的坐标是
.
【答案】(,)
【解析】解:E为AB的中点,当O,E及C共线时,OC最大,过C作CF⊥x轴于F,则∠CFO=90°,
此时由勾股定理得:
OC=1+2=3,即
∵∠CBE=90°,∴∠ECB=30°,∠BEC=60°,∴∠AEO=60°,
∵在Rt△AOB中,E为斜边AB中点,∴AE=OE,∴△AOE等边三角形,∴∠AOE=60°,∴∠COB=90°-60°=30°,
由勾股定理得:
所以点C的坐标是故答案为:
15.如图,在正方形ABCD中,AB=12,点E、F、G、H分别在AB、BC、CD、DA上,EG=13,FH=15,则四边形EFGH的面积是____.
【答案】94.5
【解析】解:如图,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1,得到矩形A1B1C1D1.
由题意得:四边形AEC1H、四边形HDGD1、四边形EBFB1、四边形CFA1G为矩形,
∴,
∵
,
∴,
∴,
∴,
∵EG=13,FH=15,
∴,,
∴,
∴,
解得.
故答案为:94.5.
三、解答题(解答时应写出文字说明、证明过程或演算步骤)
16.
已知:l∥m∥n∥k,平行线与m、m与n、n之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”。
(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线于点F.
求正方形ABCD的边长。
(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60?,△AEF是等边三角形,AE⊥k?于点E,∠AFD=90?,直线DF分别交直线l、于点G、M.求证:EC=DF.
(3)矩形ABCD为“格线四边形”,其长:宽=2:1,直接写出矩形ABCD的宽。
解答:(1)∵l∥k,BE⊥l,∴∠BFC=∠BEA=90?,∴∠ABE+∠BAE=90?,
∵四边形ABCD是正方形,∴∠ABC=90?,AB=BC.∴∠ABE+∠CBF=90?,∴∠BAE=∠CBF,
在△AED与△DGC中,∴△AED≌△GDC,∴AE=BF,
∵d1=d3=1,d2=2,∴BE=3,AE=1,在直角△ABE中,AB=BE2+AE2,
即正方形的边长是根号10;
(2)证明:如解答图②,连接AC,
∵四边形ABCD是菱形,且∠ADC=60?,∴AC=AD,
∵△AEF是等边三角形,∴AE=AF,
∵AE⊥k,∠AFD=90?,∴∠AEC=∠AFD=90?,
在Rt△AEC与Rt△AFD中,{AC=ADAE=AF,∴Rt△AEC≌Rt△AFD,∴EC=DF;
(3)过B作BE⊥l于点E,反向延长BE交k于点F.
则BE=1,BF=3,
∵四边形ABCD是矩形,∴∠ABC=90?,∴∠ABE+∠FBC=90?,
又∵直角△ABE中,∠ABE+∠EAB=90?,∴∠FBC=∠EAB,∴△AEB∽△BFC,
当AB是较短的边时,如图(a),AB=12BC,则AE=12BF=32,
在直角△ABE中,
当AB是长边时,如图(b),
故答案为:根号13或根号37除以2.
17.如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
【解答】
(1)如图1中,
∵四边形ABCD是矩形,
∴∠ADC=∠A=90?,
∴∠DCP+∠CPD=90?,
∵∠CPD+∠ADB=90?,
∴∠ADB=∠PCD,
∵∠A=∠CDP=90?,
∴△ABD∽△DPC,
∴ADCD=ABPD,
∴64=4PD,
∴PD=83,
∴t=83s时,B.
E.?D共线.
(2)如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4
易证四边形EMCQ是矩形,
∴CM=EQ=3,∠M=90?,
∴EM=EC2?CM2
∵∠DAC=∠EDM,∠ADC=∠M,
∴△ADC∽△DME,
ADDM=DCEM,,
如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4
在Rt△ECQ中,QC=DM
由△DME∽△CDA,
∴DMCD=EMAD,
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围
18.在△ABC中,AB=12,AC=BC=10,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为D,点C的对应点为E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长.
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
【答案】(1)①证明见解析;②证明见解析;③
BE=6-8;(2)BE+CE=26
.
【解析】(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AB=AD,∠BAD=60°,
∴△ABD是等边三角形;
②由①得△ABD是等边三角形,
∴AB=BD,
∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AC=AE,BC=DE,
又∵AC=BC,
∴EA=ED,
∴点B、E在AD的线段垂直平分线上,
∴BE是AD的线段垂直平分线,
∵点F在BE的延长线上,
∴BF⊥AD,?AF=DF;
③由②知BF⊥AD,AF=DF,
∴AF=DF=6,
∵AE=AC=10,
∴EF=8,
∵在等边三角形ABD中,BF=,
∴BE=BF﹣EF=;
(2)如图所示,
∵∠DAG=∠ACB,∠DAE=∠BAC,
∴∠ACB+∠BAC+∠ABC=∠DAG+∠DAE+∠ABC=180°,
又∵∠DAG+∠DAE+∠BAE=180°,
∴∠BAE=∠ABC,
∵AC=BC=AE,
∴∠BAC=∠ABC,
∴∠BAE=∠BAC,
∴AB⊥CE,且CH=HE=CE,
∵AC=BC,
∴AH=BH=AB=6,
∴CH=
则CE=2CH=16,BE=10,
∴BE+CE=10+16=26.
19.如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
(1)点E在整个运动过程中,试说明总有:CE=EF;
(2)求y与x之间关系的表达式,并写出x的取值范围.
【答案】(1)见解析;(2)y=
【解析】(1)证明:如图1,过E作MN∥AB,交AD于M,交BC于N,
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,
∴CE=EF;
如图2,同理可证明∠BAE=∠CFE,
∵BD是正方形ABCD的对角线,
∴∠ABE=∠CBE=45°
又AB=CB,BE=BE
∴△BEA≌△BEC
∴∠BAE=∠BCE
∴∠CFE=∠FCE
∴CE=FE
因此,点E在整个运动过程中,总有:CE=EF;
(2)解:在Rt△BCD中,由勾股定理得:,
∴,
由题意得:BE=2x,
∴,
由(1)知:AE=EF=EC,
分两种情况:
①当时,如图3,
∵AB=MN=10,
∴ME=FN=10-x,
∴BF=FN-BN=10-x-x=10-2x,
∴;
②当时,如图4,过E作EN⊥BC于N,
∴EN=BN=x,
∴FN=CN=10-x,
∴BF=BC-2CN=10-2(10-x)=2x-10,
∴;
综上,y与x之间关系的函数表达式为:
y=
20.如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标,4),△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
(1)
求直线BD的解析式;
(2)
求△BOH的面积;
(3)
点M在x轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)
;(2)
;
(3)
存在,N点坐标为(,)或(,3)或(,3)或(,3)
【解析】(1)
∵B点坐标,4),
∴BC=,OC=4,
∵△ODE是△OCB绕点O顺时针旋转90°得到的,
∴OD=OC=4,DE=BC=,
∴D点坐标为(4,0),E点坐标为(4,),
设直线BD的解析式为,
把B、D的坐标代入可得,,
解得:,
∴直线BD的解析式为;
(2)
设直线OE的解析式为,
把E的坐标代入可得,,
解得:,
∴直线OE的解析式为,
解方程组,得,
∴H点坐标为(,),
∵直线BD的解析式为,
令,则,
∴F点坐标为(0,3),
∴OF=3,
∴;
(3)
∵F点坐标为(0,3),D点坐标为(4,0),
∴OF=3,OD=4,,
①当DF为对角线时,四边形DNFM是菱形,如图:
∴设DM=FM=FN=,
在Rt中,OM=OD-DM=4-,
∵,
∴,
解得:,
∴N点坐标为(,3);
②D、N为对角顶点,且M点轴正半轴上时,四边形DMNF是菱形,如图:
∴DM=FN=,
∴N点坐标为(,3);
③D、N为对角顶点,且M点轴负半轴上时,四边形DFMN是菱形,如图:
∴DM=FN=,
∴N点坐标为(,3);
④当DM为对角线时,四边形DFMN是菱形,如图:
根据菱形的对称性,知:F、N关于x轴对称,
∴N点坐标为(,);
综上可知存在满足条件的N点,坐标为(,)或(,3)或(,3)或(,3).
专题02平行四边形B卷(解析版)
一、选择题(每小题只有一个选项是正确的,请将正确选项前的字母代号填写在括号内)
1.
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2020次,点B的落点依次为B1,B2,B3,…,则B2020的坐标为(
)
A.
(1345,0)
B.
(1345.5,)
C.
(1346,0)
D.
(1346.5,)
【答案】C
【解析】连接AC,如图所示.
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB=OA=1,
画出第5次、第6次、第7次翻转后的图形,如图所示.
由图可知:每翻转6次,图形向右平移4.
∵2020=336×6+4,
∴点B4向右平移1344(即336×4)到点B2020.
∵B4的坐标为(2,0),
∴B2020的坐标为(2+1344,0),
∴B2020的坐标为(1346,0).
故选:C.
2.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是(
)
A.
5cm
B.
6cm
C.
cm
D.
cm
【答案】D
【解析】解:∵四边形ABCD是菱形,AC=6cm,BD=8cm,
∴AO=CO=3cm,BO=DO=4cm,∠BOC=90°,
∴BC==5(cm),
∵S△ABC=AE×BC=BO×AC
故5AE=24,
解得:AE=(cm).
故选D.
3.
如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为(
)
A.
12
B.
C.
D.
【答案】C
【解析】如图:
连接DE,过点A作AN
垂直DE于点E,
根据题意由旋转知AD=AE,∠BAD=∠CAE,
又∵等边△ABC中,∠BAC=60°,
∴∠BAD+∠CAD=∠CAE+∠CAD,
即∠BAC=∠DAE=60°,
∴△ADE是等边三角形,
∴DE=AD=4,
又BD=3,CD=5,
∴
,
∴△CDE是直角三角形,
∵AD=4,∠ADE=60°,
∴∠DAN=30°,
∴DN=2,
由勾股定理得AN=
,
∵=,
,
,
∴,
即四边形ADCE的面积是,
故答案为:C.
4.如图,菱形的对角线,交于点,,将沿点到点的方向平移,得到,当点与点重合时,点与点之间的距离为(
)
A.
B.
C.
D.
【答案】C
【解析】由菱形的性质得
为直角三角形
故选C
5.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=8,则四边形ABCD的面积为( )
A.
32
B.
24
C.
40
D.
36
【答案】A
【解析】解:如图,作AM⊥BC、AN⊥CD,交CD的延长线于点N;
∵∠BAD=∠BCD=90°
∴四边形AMCN为矩形,∠MAN=90°;
∵∠BAD=90°,
∴∠BAM=∠DAN;
在△ABM与△ADN中,
∴△ABM≌△ADN(AAS),
∴AM=AN(设为a);△ABM与△ADN的面积相等;
∴四边形ABCD的面积=正方形AMCN的面积;
由勾股定理得:AC2=AM2+MC2,而AC=8;
∴2a2=64,a2=32,
故选:A.
6.在平面直角坐标系xOy中,点A(4,3),点B为x轴正半轴上一点,将△AOB绕其一顶点旋转180°,连接其余四个顶点得到一个四边形,若该四边形是一个轴对称图形,则满足条件的点有(
)
A.5个
B.4个
C.3个
D.2个
【答案】A.
7.
如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,
连接CE,△DEC的周长为(
)
A.10
B.11
C.12
D.13
【答案】A
8.如图,已知点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是(
)
A.
AB=CD
B.
AC=BD
C.
AC⊥BD
D.
AD=BC
【答案】A
【解析】解:∵点E、F、G、H分别是任意四边形ABCD中AD、BC、BD、AC的中点,∴EG=FH=AB,EH=FG=CD,
∵当EG=FH=
EH=FG时,四边形EGFH是菱形,
∴当AB=CD时,四边形EFGH是菱形.
故选:A.
二、填空题(不需写出解答过程,只需把答案直接填写在对应横线上)
9.如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点.当四边形ABCD满足_____
时,四边形EGFH是菱形.
【解析】本题可根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF,EG=HF,因此四边形EHFG是平行四边形,本题考查了菱形的判定,运用的是菱形的定义:一组邻边相等的平行四边形是菱形
【解答】证明:∵点E,G分别是AD,BD的中点,
∴EG∥AB,同理HF∥AB,∴EG∥HF,EG=HF=
∴四边形EGFH是平行四边形.
∵AB=CD,∴EG=EH,
∴四边形EGFH是菱形.
故答案为AB=CD.
10.已知:如图,AD、CE分别是△ABC的角平分线和中线,AD⊥CE,AD=CE=4,则BC的长等于
.
【答案】
【解析】如下图,过点B作CE垂线,交CE延长线于点F,AD与CE交于点H.
∵AD⊥EC,AD是∠EAC的角平分线
∴∠EAH=∠HAC
∴∠AEH=∠ACH,∴AE=AC,△AEC是等腰三角形
∵CE=4
∴EH=HC=2
∵CE是△ABC的中线,∴AE=EB
∵∠AEH=∠FEB,∠AHE=∠BFE=90°
∴△AEH≌△BEF
∴EF=2,FC=2+2+2=6,BF=AH
∵∠DCH=∠BCF,∠DHC=∠BFC=90°
∴△DCH∽△BCF
∴
∴3DH=BF,∴3DH=HA
∵AD=4
∴HD=1,FB=3
∴在Rt△CBF中,CB=
故答案为:
11.如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB,G、H是BC边上的点,且GH=BC,若,则=
.
【答案】2
【解析】解:连接AC、BD,如图,
∵点O是?ABCD的对称中心,
∴AC、BD交于点O,
∴S△AOB=S△BOC,
∵EF=AB,
∴S△EOF=S△AOB,
∵GH=BC,
∴S△OGH=S△BOC,
∴S△EOF:S△OGH=3:2,
∵,
∴=2.
故答案为:2.
12.如图,矩形ABCD的对角线交于点O,点E在线段AO上,且DE=DC,若∠EDO=15°,则∠DEC=______°.
【答案】55
【解析】解:设∠DEC=x,
∵DE=DC,
∴∠DCE=x,
∵四边形ABCD为矩形,
∴∠ODC=∠DCE=x,
∴∠DOE=∠OCD+∠ODC=2x,
∵△DOE内角和为180°,
∴,
解得:,
即∠DEC=,
故答案为:55.
13.
E、F是线段AB上的两点,且AB=16,AE=1,BF=3,点G是线段EF上的一动点,分别以AG、BG为斜边在AB同侧作两个等腰直角三角形,直角顶点分别为D、C,如图所示,连接CD并取中点P,连结PG,点G从E点出发运动到F点,则线段PG扫过的图形面积为______.
【答案】36
【解析】解:分别延长AD、BC交于点H,连接PH,EH,FH,
∵△ADG、△GCB为等腰直角三角形,
∴∠DGA=∠CGB=45°,
∴∠DGC=90°,
∴AH∥GC,
又∵∠HCG=90°,
∴∠HCG=∠DGC=90°,
∴DG∥HB,
∴四边形DGCH为矩形,
∵点P未DC中点,
∴点G、P、H三点共线,且P为HG的中点,
过P作MN∥于AB分别交EH、FH与M、N,
∴MN为△HEF的中位线,且MN即为点P的运动轨迹,
∴GP扫过的图形即为梯形MEFN,
∵AB=16,AE=1,BF=3,
∴EF=16-1-3=12,
∴,
过点H作HO垂直AB于O,
∴,
∴梯形的高为:,
∴,
即线段PG扫过的图形面积为36,
故答案为:36.
14.如图,在矩形ABCD中,AB=2,BC=,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则当OC为最大值时,点C的坐标是
.
【答案】(,)
【解析】解:E为AB的中点,当O,E及C共线时,OC最大,过C作CF⊥x轴于F,则∠CFO=90°,
此时由勾股定理得:
OC=1+2=3,即
∵∠CBE=90°,∴∠ECB=30°,∠BEC=60°,∴∠AEO=60°,
∵在Rt△AOB中,E为斜边AB中点,∴AE=OE,∴△AOE等边三角形,∴∠AOE=60°,∴∠COB=90°-60°=30°,
由勾股定理得:
所以点C的坐标是故答案为:
15.如图,在正方形ABCD中,AB=12,点E、F、G、H分别在AB、BC、CD、DA上,EG=13,FH=15,则四边形EFGH的面积是____.
【答案】94.5
【解析】解:如图,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1,得到矩形A1B1C1D1.
由题意得:四边形AEC1H、四边形HDGD1、四边形EBFB1、四边形CFA1G为矩形,
∴,
∵
,
∴,
∴,
∴,
∵EG=13,FH=15,
∴,,
∴,
∴,
解得.
故答案为:94.5.
三、解答题(解答时应写出文字说明、证明过程或演算步骤)
16.
已知:l∥m∥n∥k,平行线与m、m与n、n之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“格线四边形”。
(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线于点F.
求正方形ABCD的边长。
(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60?,△AEF是等边三角形,AE⊥k?于点E,∠AFD=90?,直线DF分别交直线l、于点G、M.求证:EC=DF.
(3)矩形ABCD为“格线四边形”,其长:宽=2:1,直接写出矩形ABCD的宽。
解答:(1)∵l∥k,BE⊥l,∴∠BFC=∠BEA=90?,∴∠ABE+∠BAE=90?,
∵四边形ABCD是正方形,∴∠ABC=90?,AB=BC.∴∠ABE+∠CBF=90?,∴∠BAE=∠CBF,
在△AED与△DGC中,∴△AED≌△GDC,∴AE=BF,
∵d1=d3=1,d2=2,∴BE=3,AE=1,在直角△ABE中,AB=BE2+AE2,
即正方形的边长是根号10;
(2)证明:如解答图②,连接AC,
∵四边形ABCD是菱形,且∠ADC=60?,∴AC=AD,
∵△AEF是等边三角形,∴AE=AF,
∵AE⊥k,∠AFD=90?,∴∠AEC=∠AFD=90?,
在Rt△AEC与Rt△AFD中,{AC=ADAE=AF,∴Rt△AEC≌Rt△AFD,∴EC=DF;
(3)过B作BE⊥l于点E,反向延长BE交k于点F.
则BE=1,BF=3,
∵四边形ABCD是矩形,∴∠ABC=90?,∴∠ABE+∠FBC=90?,
又∵直角△ABE中,∠ABE+∠EAB=90?,∴∠FBC=∠EAB,∴△AEB∽△BFC,
当AB是较短的边时,如图(a),AB=12BC,则AE=12BF=32,
在直角△ABE中,
当AB是长边时,如图(b),
故答案为:根号13或根号37除以2.
17.如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
【解答】
(1)如图1中,
∵四边形ABCD是矩形,
∴∠ADC=∠A=90?,
∴∠DCP+∠CPD=90?,
∵∠CPD+∠ADB=90?,
∴∠ADB=∠PCD,
∵∠A=∠CDP=90?,
∴△ABD∽△DPC,
∴ADCD=ABPD,
∴64=4PD,
∴PD=83,
∴t=83s时,B.
E.?D共线.
(2)如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4
易证四边形EMCQ是矩形,
∴CM=EQ=3,∠M=90?,
∴EM=EC2?CM2
∵∠DAC=∠EDM,∠ADC=∠M,
∴△ADC∽△DME,
ADDM=DCEM,,
如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4
在Rt△ECQ中,QC=DM
由△DME∽△CDA,
∴DMCD=EMAD,
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围
18.在△ABC中,AB=12,AC=BC=10,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为D,点C的对应点为E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长.
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
【答案】(1)①证明见解析;②证明见解析;③
BE=6-8;(2)BE+CE=26
.
【解析】(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AB=AD,∠BAD=60°,
∴△ABD是等边三角形;
②由①得△ABD是等边三角形,
∴AB=BD,
∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AC=AE,BC=DE,
又∵AC=BC,
∴EA=ED,
∴点B、E在AD的线段垂直平分线上,
∴BE是AD的线段垂直平分线,
∵点F在BE的延长线上,
∴BF⊥AD,?AF=DF;
③由②知BF⊥AD,AF=DF,
∴AF=DF=6,
∵AE=AC=10,
∴EF=8,
∵在等边三角形ABD中,BF=,
∴BE=BF﹣EF=;
(2)如图所示,
∵∠DAG=∠ACB,∠DAE=∠BAC,
∴∠ACB+∠BAC+∠ABC=∠DAG+∠DAE+∠ABC=180°,
又∵∠DAG+∠DAE+∠BAE=180°,
∴∠BAE=∠ABC,
∵AC=BC=AE,
∴∠BAC=∠ABC,
∴∠BAE=∠BAC,
∴AB⊥CE,且CH=HE=CE,
∵AC=BC,
∴AH=BH=AB=6,
∴CH=
则CE=2CH=16,BE=10,
∴BE+CE=10+16=26.
19.如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
(1)点E在整个运动过程中,试说明总有:CE=EF;
(2)求y与x之间关系的表达式,并写出x的取值范围.
【答案】(1)见解析;(2)y=
【解析】(1)证明:如图1,过E作MN∥AB,交AD于M,交BC于N,
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,
∴CE=EF;
如图2,同理可证明∠BAE=∠CFE,
∵BD是正方形ABCD的对角线,
∴∠ABE=∠CBE=45°
又AB=CB,BE=BE
∴△BEA≌△BEC
∴∠BAE=∠BCE
∴∠CFE=∠FCE
∴CE=FE
因此,点E在整个运动过程中,总有:CE=EF;
(2)解:在Rt△BCD中,由勾股定理得:,
∴,
由题意得:BE=2x,
∴,
由(1)知:AE=EF=EC,
分两种情况:
①当时,如图3,
∵AB=MN=10,
∴ME=FN=10-x,
∴BF=FN-BN=10-x-x=10-2x,
∴;
②当时,如图4,过E作EN⊥BC于N,
∴EN=BN=x,
∴FN=CN=10-x,
∴BF=BC-2CN=10-2(10-x)=2x-10,
∴;
综上,y与x之间关系的函数表达式为:
y=
20.如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标,4),△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
(1)
求直线BD的解析式;
(2)
求△BOH的面积;
(3)
点M在x轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)
;(2)
;
(3)
存在,N点坐标为(,)或(,3)或(,3)或(,3)
【解析】(1)
∵B点坐标,4),
∴BC=,OC=4,
∵△ODE是△OCB绕点O顺时针旋转90°得到的,
∴OD=OC=4,DE=BC=,
∴D点坐标为(4,0),E点坐标为(4,),
设直线BD的解析式为,
把B、D的坐标代入可得,,
解得:,
∴直线BD的解析式为;
(2)
设直线OE的解析式为,
把E的坐标代入可得,,
解得:,
∴直线OE的解析式为,
解方程组,得,
∴H点坐标为(,),
∵直线BD的解析式为,
令,则,
∴F点坐标为(0,3),
∴OF=3,
∴;
(3)
∵F点坐标为(0,3),D点坐标为(4,0),
∴OF=3,OD=4,,
①当DF为对角线时,四边形DNFM是菱形,如图:
∴设DM=FM=FN=,
在Rt中,OM=OD-DM=4-,
∵,
∴,
解得:,
∴N点坐标为(,3);
②D、N为对角顶点,且M点轴正半轴上时,四边形DMNF是菱形,如图:
∴DM=FN=,
∴N点坐标为(,3);
③D、N为对角顶点,且M点轴负半轴上时,四边形DFMN是菱形,如图:
∴DM=FN=,
∴N点坐标为(,3);
④当DM为对角线时,四边形DFMN是菱形,如图:
根据菱形的对称性,知:F、N关于x轴对称,
∴N点坐标为(,);
综上可知存在满足条件的N点,坐标为(,)或(,3)或(,3)或(,3).
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
