8-1 功与功率 课件—2020-2021学年【新教材】人教版(2019)高中物理必修第二册(41页PPT)
文档属性
| 名称 | 8-1 功与功率 课件—2020-2021学年【新教材】人教版(2019)高中物理必修第二册(41页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-02 00:00:00 | ||
图片预览








文档简介
学习目标:
1.理解功的概念.
2.掌握W=Flcos α的适用条件,会用它进行计算.(重点)
3.理解正功、负功的含义,会求多个力的总功.(重点、难点)
4.掌握变力功的求法.
5.知道功率的概念,理解功率的物理意义.
6.掌握功率的定义式????=????????,能够用????=????????解答有关的问题.(重点)
7.知道P=Fv的推导过程.(重点)
8.掌握汽车启动问题的分析方法.(难点)
9.理解额定功率和实际功率的概念.(重点)
?
复习回顾
1、初中阶段,我们已经学习过功,功的定义是什么呢?
2、功率的物理意义是什么?
力与在力的方向上移动的距离的乘积(W=FS)。
单位时间内做功的大小。
思考讨论
F拉
S
力与运动的距离不在同一直线,功该怎么求?
功
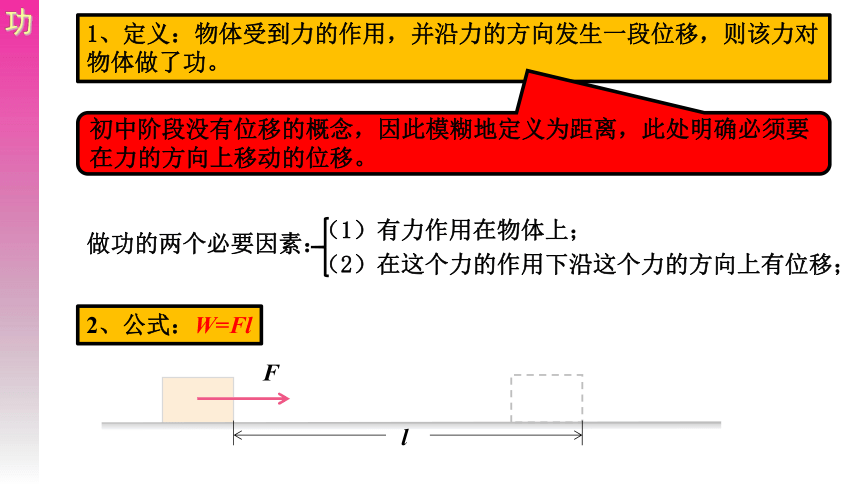
1、定义:物体受到力的作用,并沿力的方向发生一段位移,则该力对物体做了功。
初中阶段没有位移的概念,因此模糊地定义为距离,此处明确必须要在力的方向上移动的位移。
做功的两个必要因素:
(1)有力作用在物体上;
(2)在这个力的作用下沿这个力的方向上有位移;
2、公式:W=Fl
F
l
功
若力的方向与位移的方向有夹角θ,则将位移分解在力的方向上后再相乘或将力分解在位移方向后再相乘。
????=????·????????????????????
?
或 ????=????????????????????·????
?
注意事项:
① F是作用在物体上的某个力(如G、N、f 等),但一定是恒力;
② l是F的作用点发生的位移;
③α是矢量F和l的夹角;
力对物体做的功只与F、 l 、α三者有关,与物体的运动状态等因素无关。
功
3、功的单位:焦耳,简称焦,符号J
物理意义: 1J等于1N的力使物体在力的方向上发生1m位移的过程中所做的功,所以1J=1N×1m=1N·m
4、功是标量。只有大小,没有方向(但有正负之分)
5、三种不做功的情况
(1)有力无位移;
(2)有位移无力;
(3)力和位移垂直;
做功的实例
练握力时握力器在力的方向上有运动的距离,握力做功
手拉行李箱时行李箱在力的方向上有运动的位移,拉力做功。
做功的实例
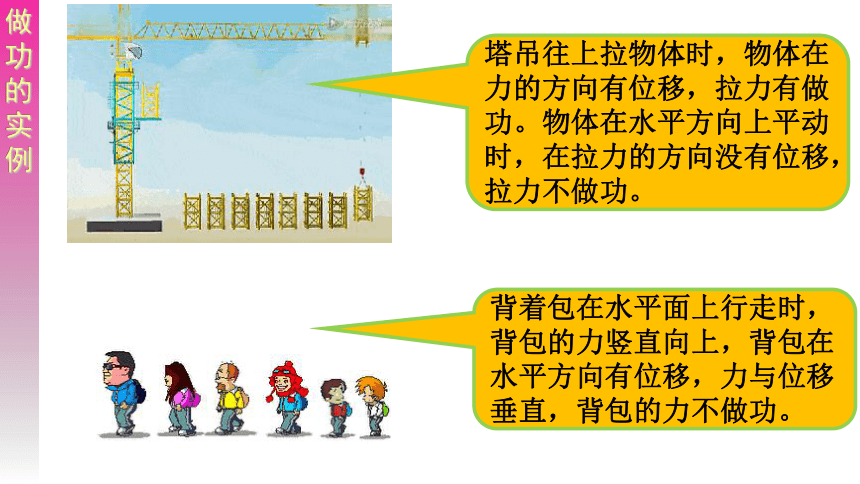
塔吊往上拉物体时,物体在力的方向有位移,拉力有做功。物体在水平方向上平动时,在拉力的方向没有位移,拉力不做功。
背着包在水平面上行走时,背包的力竖直向上,背包在水平方向有位移,力与位移垂直,背包的力不做功。
正功和负功
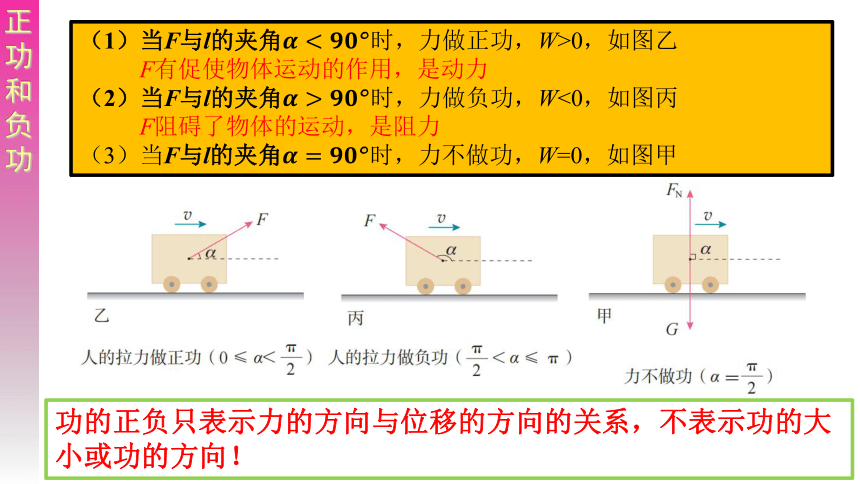
(1)当F与l的夹角????0,如图乙
F有促使物体运动的作用,是动力
(2)当F与l的夹角????>????????°时,力做负功,W<0,如图丙
F阻碍了物体的运动,是阻力
(3)当F与l的夹角????=????????°时,力不做功,W=0,如图甲
?
功的正负只表示力的方向与位移的方向的关系,不表示功的大小或功的方向!
思考讨论
刚刚我们讨论的都是单个力的情况,那一个物体受多个力作用时做的功又是多少呢?
方法一:
方法二:
先求合力,再求功。
F1、F2、F3···的合力为F合,则W总=F合·lcos????
?
先求各个力所做的功,再求这几个功的代数和。
F1做功W1,F2做功W2,F3做功W3,···,
则W总=W1+W2+W3+···
例题讲解
【例1】一个质量为 150 kg 的雪橇,受到与水平方向成 37°角斜向上方的拉力,大小为500 N,在水平地面上移动的距离为 5 m。地面对雪橇的阻力为 100 N,cos 37°= 0.8。求各力对雪橇做的总功。
解 拉力在水平方向的分力为 Fx = Fcos 37°,它所做的功为
W1 = Fx l = Fl cos 37 = 500×5×0.8 J = 2 000 J
阻力与运动方向相反,两者夹角为 180°,它所做的功为
W2 = F 阻 l cos 180°=- 100×5 J =- 500 J
力对物体所做的总功为二者的代数和,即
W = W1 + W2 = 2 000 J - 500 J = 1 500 J
力对雪橇所做的总功是 1 500 J。
变力做功
这里特别强调了适用于恒力做功,那变力做功可以求出功吗?
????=????????
?
F一定是恒力,即大小和方向都不变
变力做功
①微元法求变力做功
将运动的过程分成很多小段,在这些小段中,力可以看作恒力,可以使用恒力做功的公式,最后再求数量和。
【例2】一辆马车在力F=100N的作用下绕半径为50m的圆形轨道做匀速圆周运动,当车运动一周回到原位置时,车子克服阻力所做的功为多少?
分析:阻力的方向时刻在变,是变力做功的问题,不能直接由功的公式计算。但可以将这个过程分成很多小段,当每个小段足够小时,路程可以看成是位移,可以使用恒力做功的方式进行求解。
Δx
Δs
F
解:Wf =fΔs1cosπ+fΔs2cosπ+fΔs3cosπ+fΔs4cosπ+……
= – fs= – Fs = – F×2πR= – 3.14 ×104 J
W克= – Wf= 3.14 ×104 J
变力做功
②平均值法求变力做功
如果可以将力的整个过程作用的平均值求出来,也可以将整个平均值作为恒力来使用。
【例3】用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比.在铁锤击第一次时,能把铁钉击入木块内1cm,问击第二次时,能击入多少深度 ? (设铁锤每次做功相等)
解:第一次击入深度为x1,平均阻力F1= 12× kx1,做功为W1= F1 x1=12×kx21.
第二次击入深度为x1到x2,
平均阻力F2=12× k(x2+x1), 位移为x2-x1,
做功为W2= F2(x2-x1)=12× k(x22-x21).
两次做功相等:W1=W2.
解后有:x2=2x1=1.41cm. 所以△x=x2-x1=0.41cm.
?
分析:铁锤每次做功都用来克服铁钉阻力做的功,但摩擦阻力不是恒力,其大小与深度成正比,F=-f=kx,可用平均阻力来代替.如图
x1
x2
变力做功
③图像法求变力做功
如果可以画出F-x图像,可以利用F-x图像所围成的面积大小就是功的大小的方式来进行求解。
【例3】用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比.在铁锤击第一次时,能把铁钉击入木块内1cm,问击第二次时,能击入多少深度 ? (设铁锤每次做功相等)
分析:恒力做功时,F与x图象如右图,W=S= F0 x0
x
F
O
x0
F0
解:因为阻力F=kx,以F为纵坐标,F方向上的位移x为横坐标,
作出F-x图像,如右下图,
W2=kx1△x+k(x1+△x)△x+ x+k(x1+2△x)△x+……
曲线下面积的值等于F对铁钉做的功. (示功图)
因S1 = S2 (面积),即:12× kx12=12× k(x2+x1)(x2-x1),
解后有:x2= 2x1=1.41cm.
∴ △x=x2-x1=0.41cm.
?
x
F
O
x1
x2
kx1
kx2
例题讲解
【例4】关于功的论述,下列说法正确的是( )
A、大的力一定比小的力做的功多
B、+5J的功比-5J的功多
C、+10J功比+5J的功多
D、+5J的功与-5J的功方向相反
C
点拨:功的正负不表示功的大小
例题讲解
【例5】两质量相等的物体A、B分别放在粗糙水平面上和光滑的水平面上,在同样的拉力F作用下,产生相同的位移S,则拉力( )
A、对A做的功多 B、对B做功多
C、一样多 D、以上都有可能
粗糙 光滑
A B
F F
θ θ
C
点拨:力对物体做的功只与F、 l 、 α三者有关,与物体的运动状态等因素无关
例题讲解
【例6】一学生用100N的力将质量为0.5kg的球迅速踢出,球在水平路面上滚出20m远,则该学生对球做的功是( )
A、2000J B、1000J
C、16J D、无法确定
D
点拨:公式中F为恒力,且F、l必须具有同时性、同体性。
例题讲解
【例7】如图示,一个质量m=150kg的雪橇,受到与水平方向成37°角的斜向上方的拉力F=500N,在水平地面上移动的距离为5m,物体与地面间的滑动摩擦力f=100N。(cos37o=0.8)求:
(1)各个力对物体所做的功;
(2)各个力对物体做功的代数和。
(3)物体所受的合力;
(4)合力对物体做的功。
F
α
mg
f
FN
解:(1)拉力F对物体所做的功为W1= Flcos37°=2000J
摩擦力F阻对物体所做的功为W2= F阻lcos180°= -500J
(2)各力做功的代数和 W=W1+W2=1500J
(3)物体所受的合力F合=Fcos37°- F阻=300N
(4)合力对物体所做的功 W= F合l=1500J
最后的麦客
思考讨论
古老的职业——麦客,为何在当代会受到生存的威胁?
麦客一天能收割1亩地,收割机一天能收割100-200亩地,与传统的手工收割相比,收割机不仅效率高,还更安全,对人体更无害,工序更简单。
效率:相同时间内做功的多少,做功越多,工作效率就越高。此次的效率,我们又叫功率。
功率
1.定义:功跟完成这些功所用时间的比值,叫做功率。
物理意义:单位时间内物体做功的大小,表示物体做功的快慢。
3.功率的表达式:????=????????
?
2.符号:P
4.单位:在国际单位制中,功率的单位是瓦特,简称瓦,符号是W,1W=1J/s 常用单位:kW 1kW=1000W
功率是标量,只有大小没有方向
例题讲解
【例8】一台机器用2分钟时间做了6×104J的功,这台机器的功率是多少?
解:由????=????????可得????=6×1042×60????=500????
?
【例9】关于功率,下列说法中正确的是( )
A、功率是说明做功多少的物理量
B、功率是说明力做功快慢的物理量
C、做功时间越长,功率一定小
D、力做功越多,功率一定大
B
功率的影响因素:功的大小和做功的时间
思考讨论
什么是额定功率?这个参数对汽车来说意味着什么?
额定功率与实际功率
(1)额定功率:指机器正常条件下可以长时间工作的最大输出功率。
(2)实际功率:指机器工作中实际输出的功率。
如刚刚汽车的额定功率、灯泡铭牌上的额定功率。
例如汽车低速平地行驶时的功率、电压不足时电灯的功率
实际功率总是小于额定功率。实际功率如果大于额定功率容易将机器损坏。
机车发动机的功率指牵引力的功率而不是合外力或阻力的功率 。起重机调起货物的功率指钢绳拉力的功率。
功率的另一种表示方式
W=Flcosα
P=
t
W
P=Fvcosα
P=
t
Flcosα
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcosα
P=Fvcosα
v=
t
l
功率的另一种表达形式P=Fvcos α (α是F与v的夹角)
功率的另一种表示方式
P=Fv
(1)P一定,F∝1????,功率一定时,速度越小,力越大
?
(2)V一定,P∝F,速度一定时,力越大,功率越大
(3)F一定,P ∝V,力一定时,速度越大,功率越大
汽车爬坡时,换低速挡,换取大的动力
汽车上坡,不减速,加油
吊车匀速吊重物,V越大, P也越大
例题讲解
【例10】发动机的额定功率是汽车长时间行驶时所能输出的最大功率。某型号汽车发动机的额定功率为 60 kW,在水平路面上行驶时受到的阻力是 1 800 N,求发动机在额定功率下汽车匀速行驶的速度。假定汽车行驶速度为 54 km/h 时受到的阻力不变,此时发动机输出的实际功率是多少?
分析
实际功率不一定总等于额定功率,大多数情况下输出的实际功率都比额定功率小,但在需要时,短时间也可以输出更大的功率。
题目中说“受到的阻力不变”,表明本题对于较低速度行驶时发动机的输出功率只要求估算。
例题讲解
【例10】发动机的额定功率是汽车长时间行驶时所能输出的最大功率。某型号汽车发动机的额定功率为 60 kW,在水平路面上行驶时受到的阻力是 1 800 N,求发动机在额定功率下汽车匀速行驶的速度。假定汽车行驶速度为 54 km/h 时受到的阻力不变,此时发动机输出的实际功率是多少?
解 汽车在水平路面上匀速行驶时,受到的牵引力
F = F 阻= 1 800 N
由于 P = Fv,所以额定功率下的速度
v = ???????? = 600001800????/????= 33.3 m/s = 120 km/h
当汽车以速度 v = 54 km/h = 15 m/s 行驶时,有
P = Fv = 1 800×15 W = 27 kW
汽车以额定功率匀速行驶时的速度为 120 km/h。汽车以 54 km/h 的速度行驶时,发动机输出的实际功率为 27 kW。
?
例题讲解
【例11】马拉着车在20分内以18Km/h的速度匀速前进,如果马的拉力为300N,求马拉车的功率。
解: 由于F=300N, S=5 × 1200m=6000m,
t=20min=1200s v=????????=60001200m/s
所以马拉车的功率:
P=????????=Fv=300×5W=1500 W
?
关于平均功率和瞬时功率
平均功率:描述在一段时间内做功的平均快慢
????=????????
?
瞬时功率:表示在某一时刻做功的快慢
当 t 表示一段时间时,此式表示平均功率
当 t 很短很短时,此式表示瞬时功率
P=Fvcos α
若 v 表示平均速度,则P 表示平均功率
若v表示瞬时速度,则P 表示瞬时功率
例题讲解
【例12】一台起重机将静止在地面上、质量为m=1.0×103 kg的货物匀加速竖直吊起,在2 s末货物的速度v=4 m/s.(g取10 m/s2,不计额外功)求:
(1)起重机在这2 s内的平均功率;
(2)起重机在2 s末的瞬时功率.
解 设货物所受的拉力为F,加速度为a,则
(1)由a=??????????得,a=2 m/s2
F=mg+ma=1.0×103×10 N+1.0×103×2 N=1.2×104 N
2 s内货物上升的高度h=12at2=4 m
起重机在这2 s内对货物所做的功W=F·h=1.2×104×4 J=4.8×104 J
起重机在这2 s内的平均功率P=????????=4.8×????????????2W=2.4×104 W.
(2)起重机在2 s末的瞬时功率
P=Fv=1.2×104×4.0 W=4.8×104 W.
?
思考
【例13】每年春节前,温州农村都有捣年糕的习俗,借此来寓意“年年发财、步步高升”.捣年糕时,一人将“石杵”一起一落挥动,另一人在“石杵”挥动的间隙迅速翻动米粉团,直到米粉团柔软而有弹性.已知“石杵”质量为20 kg,每分钟上下挥动20下,每次重心上升的高度约为90 cm,则人挥动“石杵”做功的平均功率约为( )
A.60 W B.120 W C.180 W D.540 W
A
【解析】挥动“石杵”一次所做的功W=mgh=20×10×0.9 J=180 J;1 min内做的总功W总=nW=20×180 J=3 600 J,则人挥动“石杵”做功的平均功率??=????????=60 W,故A正确,B、C、D错误.
?
机车启动问题
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
①当汽车以额定功率P启动时,F与v成反比。
F
v
O
f
v
t
vm
P
t
P额
在速度未达到最大速度vm之前,牵引力与速度的关系为P=F牵·v=(ma+f)·v,由于v↑,所以F牵↓,a↓,当v达到最大速度vm时,F牵=f,a=0,汽车做匀速直线运动。
O
O
O
a
t
机车启动问题
②当汽车以恒定加速度a启动时,开始时F恒定,达到某一速度之后P恒定。
F
v
O
f
v
t
vm
P
t
P额
O
O
O
a
t
F=ma
t1
t2
t1
t2
t1
t2
t1
t2
(1)在速度未达到vm前,汽车做加速度为a的匀加速直线运动,牵引力与速度的关系为????=(????????+????)·????,P↑,v↑,a不变,直到P到达额定最大功率P额,此时有????????’=????额(????????+????),vm’为做匀加速直线运动的最大速度。
?
(2)当汽车达到匀加速直线运动的最大速度之后,P达到最大功率P额,功率开始恒定不变,在额定功率下做变加速直线运动,直到达到最大速度vm,此过程牵引力与速度的关系为P=(ma’+f )·v,P不变,a’↓,v↑。
例题讲解
汽车以额定功率在平直公路行驶时,若前方遇到了一段较陡的上坡路段,汽车司机要做好什么调整,才能确保汽车驶到坡顶?为什么?
汽车上坡需要较大的牵引力,因此需要调整为低速挡,以速度换动力。
例题讲解
【例14】质量为2t的汽车,发动机输出功率为30kW,在水平公路上能达到的最大速度为15m/s,则汽车速度为10m/s时的加速度为多大?
解:由P=Fv可得汽车在速度最大时的牵引力为
F牵=????额????????=30000????15????/????=2000????
由相互作用力可得f=F牵=2000N
汽车额定功率行驶,有P额=(ma+f )·v,可得加速度????=????额?????????????
代入数据可得a=0.5m/s2
?
分析:发动机输出功率即为额定功率,因此该汽车启动类型为额定功率启动。此时有P额=(ma+f )·v
例题讲解
【例15】一列高速列车总质量m=465 t,其额定功率P=5 300 kW,在水平直轨道上行驶时,轨道对列车的阻力F阻是车重的0.018.列车以额定功率工作,取重力加速度g=10 m/s2,求:
(1)当行驶速度v= 10 m/s时,列车的牵引力大小和加速度大小;
(2)列车在水平直轨道上行驶的最大速度大小.
解:由题意可知F阻=0.018mg.设列车以额定功率工作,当行驶速度v=10 m/s时,牵引力为F1;行驶速度达到最大值vmax时,牵引力为F2.
(1)由P=F1v得F1=????????=5.3×????????????10 N=5.3×105 N
根据牛顿第二定律,有F1-F阻=ma,解得a=0.96 m/s2.
(2)当F2=F阻时,列车行驶速度最大
由P=F2vmax得vmax=????????阻=63.3 m/s.
?
例题讲解
【例16】质量为m=5×103 kg的汽车在水平公路上行驶,阻力是车重的0.1.让车保持额定功率为60 kW,从静止开始行驶,求(g取10 m/s2):
(1)汽车达到的最大速度vm大小;
(2)汽车车速v1=2 m/s时的加速度大小.
解:(1)由P=Fv=Ffvm得
vm=????????????=????0.1????????=60×????????????0.1×????×????????????×???????? m/s=12 m/s.
(2)由P=Fv得F=????????
当v1=2 m/s时,
F1=????????1=60×????????????2 N=3×104 N
由牛顿第二定律得F1-Ff=ma,所以
a=????1?0.1????????????=3×?????????????????.????×????×????????????×????????5×???????????? m/s2=5 m/s2.
?
谢谢观看,完成课后作业!
1.理解功的概念.
2.掌握W=Flcos α的适用条件,会用它进行计算.(重点)
3.理解正功、负功的含义,会求多个力的总功.(重点、难点)
4.掌握变力功的求法.
5.知道功率的概念,理解功率的物理意义.
6.掌握功率的定义式????=????????,能够用????=????????解答有关的问题.(重点)
7.知道P=Fv的推导过程.(重点)
8.掌握汽车启动问题的分析方法.(难点)
9.理解额定功率和实际功率的概念.(重点)
?
复习回顾
1、初中阶段,我们已经学习过功,功的定义是什么呢?
2、功率的物理意义是什么?
力与在力的方向上移动的距离的乘积(W=FS)。
单位时间内做功的大小。
思考讨论
F拉
S
力与运动的距离不在同一直线,功该怎么求?
功
1、定义:物体受到力的作用,并沿力的方向发生一段位移,则该力对物体做了功。
初中阶段没有位移的概念,因此模糊地定义为距离,此处明确必须要在力的方向上移动的位移。
做功的两个必要因素:
(1)有力作用在物体上;
(2)在这个力的作用下沿这个力的方向上有位移;
2、公式:W=Fl
F
l
功
若力的方向与位移的方向有夹角θ,则将位移分解在力的方向上后再相乘或将力分解在位移方向后再相乘。
????=????·????????????????????
?
或 ????=????????????????????·????
?
注意事项:
① F是作用在物体上的某个力(如G、N、f 等),但一定是恒力;
② l是F的作用点发生的位移;
③α是矢量F和l的夹角;
力对物体做的功只与F、 l 、α三者有关,与物体的运动状态等因素无关。
功
3、功的单位:焦耳,简称焦,符号J
物理意义: 1J等于1N的力使物体在力的方向上发生1m位移的过程中所做的功,所以1J=1N×1m=1N·m
4、功是标量。只有大小,没有方向(但有正负之分)
5、三种不做功的情况
(1)有力无位移;
(2)有位移无力;
(3)力和位移垂直;
做功的实例
练握力时握力器在力的方向上有运动的距离,握力做功
手拉行李箱时行李箱在力的方向上有运动的位移,拉力做功。
做功的实例
塔吊往上拉物体时,物体在力的方向有位移,拉力有做功。物体在水平方向上平动时,在拉力的方向没有位移,拉力不做功。
背着包在水平面上行走时,背包的力竖直向上,背包在水平方向有位移,力与位移垂直,背包的力不做功。
正功和负功
(1)当F与l的夹角????0,如图乙
F有促使物体运动的作用,是动力
(2)当F与l的夹角????>????????°时,力做负功,W<0,如图丙
F阻碍了物体的运动,是阻力
(3)当F与l的夹角????=????????°时,力不做功,W=0,如图甲
?
功的正负只表示力的方向与位移的方向的关系,不表示功的大小或功的方向!
思考讨论
刚刚我们讨论的都是单个力的情况,那一个物体受多个力作用时做的功又是多少呢?
方法一:
方法二:
先求合力,再求功。
F1、F2、F3···的合力为F合,则W总=F合·lcos????
?
先求各个力所做的功,再求这几个功的代数和。
F1做功W1,F2做功W2,F3做功W3,···,
则W总=W1+W2+W3+···
例题讲解
【例1】一个质量为 150 kg 的雪橇,受到与水平方向成 37°角斜向上方的拉力,大小为500 N,在水平地面上移动的距离为 5 m。地面对雪橇的阻力为 100 N,cos 37°= 0.8。求各力对雪橇做的总功。
解 拉力在水平方向的分力为 Fx = Fcos 37°,它所做的功为
W1 = Fx l = Fl cos 37 = 500×5×0.8 J = 2 000 J
阻力与运动方向相反,两者夹角为 180°,它所做的功为
W2 = F 阻 l cos 180°=- 100×5 J =- 500 J
力对物体所做的总功为二者的代数和,即
W = W1 + W2 = 2 000 J - 500 J = 1 500 J
力对雪橇所做的总功是 1 500 J。
变力做功
这里特别强调了适用于恒力做功,那变力做功可以求出功吗?
????=????????
?
F一定是恒力,即大小和方向都不变
变力做功
①微元法求变力做功
将运动的过程分成很多小段,在这些小段中,力可以看作恒力,可以使用恒力做功的公式,最后再求数量和。
【例2】一辆马车在力F=100N的作用下绕半径为50m的圆形轨道做匀速圆周运动,当车运动一周回到原位置时,车子克服阻力所做的功为多少?
分析:阻力的方向时刻在变,是变力做功的问题,不能直接由功的公式计算。但可以将这个过程分成很多小段,当每个小段足够小时,路程可以看成是位移,可以使用恒力做功的方式进行求解。
Δx
Δs
F
解:Wf =fΔs1cosπ+fΔs2cosπ+fΔs3cosπ+fΔs4cosπ+……
= – fs= – Fs = – F×2πR= – 3.14 ×104 J
W克= – Wf= 3.14 ×104 J
变力做功
②平均值法求变力做功
如果可以将力的整个过程作用的平均值求出来,也可以将整个平均值作为恒力来使用。
【例3】用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比.在铁锤击第一次时,能把铁钉击入木块内1cm,问击第二次时,能击入多少深度 ? (设铁锤每次做功相等)
解:第一次击入深度为x1,平均阻力F1= 12× kx1,做功为W1= F1 x1=12×kx21.
第二次击入深度为x1到x2,
平均阻力F2=12× k(x2+x1), 位移为x2-x1,
做功为W2= F2(x2-x1)=12× k(x22-x21).
两次做功相等:W1=W2.
解后有:x2=2x1=1.41cm. 所以△x=x2-x1=0.41cm.
?
分析:铁锤每次做功都用来克服铁钉阻力做的功,但摩擦阻力不是恒力,其大小与深度成正比,F=-f=kx,可用平均阻力来代替.如图
x1
x2
变力做功
③图像法求变力做功
如果可以画出F-x图像,可以利用F-x图像所围成的面积大小就是功的大小的方式来进行求解。
【例3】用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比.在铁锤击第一次时,能把铁钉击入木块内1cm,问击第二次时,能击入多少深度 ? (设铁锤每次做功相等)
分析:恒力做功时,F与x图象如右图,W=S= F0 x0
x
F
O
x0
F0
解:因为阻力F=kx,以F为纵坐标,F方向上的位移x为横坐标,
作出F-x图像,如右下图,
W2=kx1△x+k(x1+△x)△x+ x+k(x1+2△x)△x+……
曲线下面积的值等于F对铁钉做的功. (示功图)
因S1 = S2 (面积),即:12× kx12=12× k(x2+x1)(x2-x1),
解后有:x2= 2x1=1.41cm.
∴ △x=x2-x1=0.41cm.
?
x
F
O
x1
x2
kx1
kx2
例题讲解
【例4】关于功的论述,下列说法正确的是( )
A、大的力一定比小的力做的功多
B、+5J的功比-5J的功多
C、+10J功比+5J的功多
D、+5J的功与-5J的功方向相反
C
点拨:功的正负不表示功的大小
例题讲解
【例5】两质量相等的物体A、B分别放在粗糙水平面上和光滑的水平面上,在同样的拉力F作用下,产生相同的位移S,则拉力( )
A、对A做的功多 B、对B做功多
C、一样多 D、以上都有可能
粗糙 光滑
A B
F F
θ θ
C
点拨:力对物体做的功只与F、 l 、 α三者有关,与物体的运动状态等因素无关
例题讲解
【例6】一学生用100N的力将质量为0.5kg的球迅速踢出,球在水平路面上滚出20m远,则该学生对球做的功是( )
A、2000J B、1000J
C、16J D、无法确定
D
点拨:公式中F为恒力,且F、l必须具有同时性、同体性。
例题讲解
【例7】如图示,一个质量m=150kg的雪橇,受到与水平方向成37°角的斜向上方的拉力F=500N,在水平地面上移动的距离为5m,物体与地面间的滑动摩擦力f=100N。(cos37o=0.8)求:
(1)各个力对物体所做的功;
(2)各个力对物体做功的代数和。
(3)物体所受的合力;
(4)合力对物体做的功。
F
α
mg
f
FN
解:(1)拉力F对物体所做的功为W1= Flcos37°=2000J
摩擦力F阻对物体所做的功为W2= F阻lcos180°= -500J
(2)各力做功的代数和 W=W1+W2=1500J
(3)物体所受的合力F合=Fcos37°- F阻=300N
(4)合力对物体所做的功 W= F合l=1500J
最后的麦客
思考讨论
古老的职业——麦客,为何在当代会受到生存的威胁?
麦客一天能收割1亩地,收割机一天能收割100-200亩地,与传统的手工收割相比,收割机不仅效率高,还更安全,对人体更无害,工序更简单。
效率:相同时间内做功的多少,做功越多,工作效率就越高。此次的效率,我们又叫功率。
功率
1.定义:功跟完成这些功所用时间的比值,叫做功率。
物理意义:单位时间内物体做功的大小,表示物体做功的快慢。
3.功率的表达式:????=????????
?
2.符号:P
4.单位:在国际单位制中,功率的单位是瓦特,简称瓦,符号是W,1W=1J/s 常用单位:kW 1kW=1000W
功率是标量,只有大小没有方向
例题讲解
【例8】一台机器用2分钟时间做了6×104J的功,这台机器的功率是多少?
解:由????=????????可得????=6×1042×60????=500????
?
【例9】关于功率,下列说法中正确的是( )
A、功率是说明做功多少的物理量
B、功率是说明力做功快慢的物理量
C、做功时间越长,功率一定小
D、力做功越多,功率一定大
B
功率的影响因素:功的大小和做功的时间
思考讨论
什么是额定功率?这个参数对汽车来说意味着什么?
额定功率与实际功率
(1)额定功率:指机器正常条件下可以长时间工作的最大输出功率。
(2)实际功率:指机器工作中实际输出的功率。
如刚刚汽车的额定功率、灯泡铭牌上的额定功率。
例如汽车低速平地行驶时的功率、电压不足时电灯的功率
实际功率总是小于额定功率。实际功率如果大于额定功率容易将机器损坏。
机车发动机的功率指牵引力的功率而不是合外力或阻力的功率 。起重机调起货物的功率指钢绳拉力的功率。
功率的另一种表示方式
W=Flcosα
P=
t
W
P=Fvcosα
P=
t
Flcosα
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcosα
P=Fvcosα
v=
t
l
功率的另一种表达形式P=Fvcos α (α是F与v的夹角)
功率的另一种表示方式
P=Fv
(1)P一定,F∝1????,功率一定时,速度越小,力越大
?
(2)V一定,P∝F,速度一定时,力越大,功率越大
(3)F一定,P ∝V,力一定时,速度越大,功率越大
汽车爬坡时,换低速挡,换取大的动力
汽车上坡,不减速,加油
吊车匀速吊重物,V越大, P也越大
例题讲解
【例10】发动机的额定功率是汽车长时间行驶时所能输出的最大功率。某型号汽车发动机的额定功率为 60 kW,在水平路面上行驶时受到的阻力是 1 800 N,求发动机在额定功率下汽车匀速行驶的速度。假定汽车行驶速度为 54 km/h 时受到的阻力不变,此时发动机输出的实际功率是多少?
分析
实际功率不一定总等于额定功率,大多数情况下输出的实际功率都比额定功率小,但在需要时,短时间也可以输出更大的功率。
题目中说“受到的阻力不变”,表明本题对于较低速度行驶时发动机的输出功率只要求估算。
例题讲解
【例10】发动机的额定功率是汽车长时间行驶时所能输出的最大功率。某型号汽车发动机的额定功率为 60 kW,在水平路面上行驶时受到的阻力是 1 800 N,求发动机在额定功率下汽车匀速行驶的速度。假定汽车行驶速度为 54 km/h 时受到的阻力不变,此时发动机输出的实际功率是多少?
解 汽车在水平路面上匀速行驶时,受到的牵引力
F = F 阻= 1 800 N
由于 P = Fv,所以额定功率下的速度
v = ???????? = 600001800????/????= 33.3 m/s = 120 km/h
当汽车以速度 v = 54 km/h = 15 m/s 行驶时,有
P = Fv = 1 800×15 W = 27 kW
汽车以额定功率匀速行驶时的速度为 120 km/h。汽车以 54 km/h 的速度行驶时,发动机输出的实际功率为 27 kW。
?
例题讲解
【例11】马拉着车在20分内以18Km/h的速度匀速前进,如果马的拉力为300N,求马拉车的功率。
解: 由于F=300N, S=5 × 1200m=6000m,
t=20min=1200s v=????????=60001200m/s
所以马拉车的功率:
P=????????=Fv=300×5W=1500 W
?
关于平均功率和瞬时功率
平均功率:描述在一段时间内做功的平均快慢
????=????????
?
瞬时功率:表示在某一时刻做功的快慢
当 t 表示一段时间时,此式表示平均功率
当 t 很短很短时,此式表示瞬时功率
P=Fvcos α
若 v 表示平均速度,则P 表示平均功率
若v表示瞬时速度,则P 表示瞬时功率
例题讲解
【例12】一台起重机将静止在地面上、质量为m=1.0×103 kg的货物匀加速竖直吊起,在2 s末货物的速度v=4 m/s.(g取10 m/s2,不计额外功)求:
(1)起重机在这2 s内的平均功率;
(2)起重机在2 s末的瞬时功率.
解 设货物所受的拉力为F,加速度为a,则
(1)由a=??????????得,a=2 m/s2
F=mg+ma=1.0×103×10 N+1.0×103×2 N=1.2×104 N
2 s内货物上升的高度h=12at2=4 m
起重机在这2 s内对货物所做的功W=F·h=1.2×104×4 J=4.8×104 J
起重机在这2 s内的平均功率P=????????=4.8×????????????2W=2.4×104 W.
(2)起重机在2 s末的瞬时功率
P=Fv=1.2×104×4.0 W=4.8×104 W.
?
思考
【例13】每年春节前,温州农村都有捣年糕的习俗,借此来寓意“年年发财、步步高升”.捣年糕时,一人将“石杵”一起一落挥动,另一人在“石杵”挥动的间隙迅速翻动米粉团,直到米粉团柔软而有弹性.已知“石杵”质量为20 kg,每分钟上下挥动20下,每次重心上升的高度约为90 cm,则人挥动“石杵”做功的平均功率约为( )
A.60 W B.120 W C.180 W D.540 W
A
【解析】挥动“石杵”一次所做的功W=mgh=20×10×0.9 J=180 J;1 min内做的总功W总=nW=20×180 J=3 600 J,则人挥动“石杵”做功的平均功率??=????????=60 W,故A正确,B、C、D错误.
?
机车启动问题
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
①当汽车以额定功率P启动时,F与v成反比。
F
v
O
f
v
t
vm
P
t
P额
在速度未达到最大速度vm之前,牵引力与速度的关系为P=F牵·v=(ma+f)·v,由于v↑,所以F牵↓,a↓,当v达到最大速度vm时,F牵=f,a=0,汽车做匀速直线运动。
O
O
O
a
t
机车启动问题
②当汽车以恒定加速度a启动时,开始时F恒定,达到某一速度之后P恒定。
F
v
O
f
v
t
vm
P
t
P额
O
O
O
a
t
F=ma
t1
t2
t1
t2
t1
t2
t1
t2
(1)在速度未达到vm前,汽车做加速度为a的匀加速直线运动,牵引力与速度的关系为????=(????????+????)·????,P↑,v↑,a不变,直到P到达额定最大功率P额,此时有????????’=????额(????????+????),vm’为做匀加速直线运动的最大速度。
?
(2)当汽车达到匀加速直线运动的最大速度之后,P达到最大功率P额,功率开始恒定不变,在额定功率下做变加速直线运动,直到达到最大速度vm,此过程牵引力与速度的关系为P=(ma’+f )·v,P不变,a’↓,v↑。
例题讲解
汽车以额定功率在平直公路行驶时,若前方遇到了一段较陡的上坡路段,汽车司机要做好什么调整,才能确保汽车驶到坡顶?为什么?
汽车上坡需要较大的牵引力,因此需要调整为低速挡,以速度换动力。
例题讲解
【例14】质量为2t的汽车,发动机输出功率为30kW,在水平公路上能达到的最大速度为15m/s,则汽车速度为10m/s时的加速度为多大?
解:由P=Fv可得汽车在速度最大时的牵引力为
F牵=????额????????=30000????15????/????=2000????
由相互作用力可得f=F牵=2000N
汽车额定功率行驶,有P额=(ma+f )·v,可得加速度????=????额?????????????
代入数据可得a=0.5m/s2
?
分析:发动机输出功率即为额定功率,因此该汽车启动类型为额定功率启动。此时有P额=(ma+f )·v
例题讲解
【例15】一列高速列车总质量m=465 t,其额定功率P=5 300 kW,在水平直轨道上行驶时,轨道对列车的阻力F阻是车重的0.018.列车以额定功率工作,取重力加速度g=10 m/s2,求:
(1)当行驶速度v= 10 m/s时,列车的牵引力大小和加速度大小;
(2)列车在水平直轨道上行驶的最大速度大小.
解:由题意可知F阻=0.018mg.设列车以额定功率工作,当行驶速度v=10 m/s时,牵引力为F1;行驶速度达到最大值vmax时,牵引力为F2.
(1)由P=F1v得F1=????????=5.3×????????????10 N=5.3×105 N
根据牛顿第二定律,有F1-F阻=ma,解得a=0.96 m/s2.
(2)当F2=F阻时,列车行驶速度最大
由P=F2vmax得vmax=????????阻=63.3 m/s.
?
例题讲解
【例16】质量为m=5×103 kg的汽车在水平公路上行驶,阻力是车重的0.1.让车保持额定功率为60 kW,从静止开始行驶,求(g取10 m/s2):
(1)汽车达到的最大速度vm大小;
(2)汽车车速v1=2 m/s时的加速度大小.
解:(1)由P=Fv=Ffvm得
vm=????????????=????0.1????????=60×????????????0.1×????×????????????×???????? m/s=12 m/s.
(2)由P=Fv得F=????????
当v1=2 m/s时,
F1=????????1=60×????????????2 N=3×104 N
由牛顿第二定律得F1-Ff=ma,所以
a=????1?0.1????????????=3×?????????????????.????×????×????????????×????????5×???????????? m/s2=5 m/s2.
?
谢谢观看,完成课后作业!
