2020-2021学年高二下学期物理人教版选修3-4课件:11.3 简谐运动的回复力和能量(26页PPT)
文档属性
| 名称 | 2020-2021学年高二下学期物理人教版选修3-4课件:11.3 简谐运动的回复力和能量(26页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-02 23:01:29 | ||
图片预览







文档简介
第十一章 机械振动
3 简谐运动的回复力和能量
导学探究 如图2所示为一个水平方向的弹簧振子模型(水平杆光滑),O点为振子的平衡位置,A、O间和B、O间距离都是x.
(1)振子在O点时受到几个力的作用?分别是什么力?
一、简谐运动的回复力
重点探究
图2
(2)振子在A、B点时受到哪些力的作用?
(3)除重力、支持力、弹簧弹力外,振子在O、A、B点还受到回复力的作用吗?回复力有什么特点?
一、简谐运动的回复力
1.定义:
2.特点:
按力的作用效果命名,方向始终指向平衡位置
使振子回到平衡位置的力
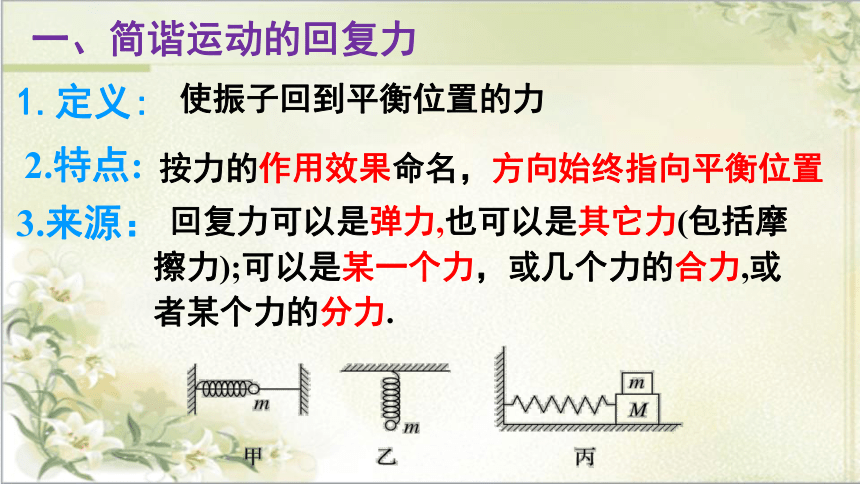
3.来源:
回复力可以是弹力,也可以是其它力(包括摩擦力);可以是某一个力,或几个力的合力,或者某个力的分力.
1.回复力
回复力是指将振动的物体拉回到平衡位置的力,回复力为零的位置就是平衡位置.
知识深化
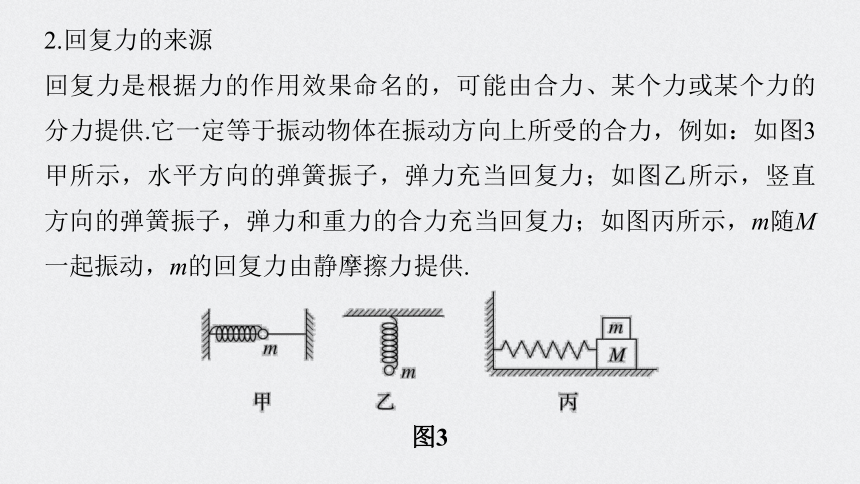
2.回复力的来源
回复力是根据力的作用效果命名的,可能由合力、某个力或某个力的分力提供.它一定等于振动物体在振动方向上所受的合力,例如:如图3甲所示,水平方向的弹簧振子,弹力充当回复力;如图乙所示,竖直方向的弹簧振子,弹力和重力的合力充当回复力;如图丙所示,m随M一起振动,m的回复力由静摩擦力提供.
图3
3.回复力公式:F=-kx
(1)k是比例系数,其数值由振动系统决定,与振幅无关.对于水平弹簧振子,回复力仅由弹力提供,k为劲度系数.
(2)“-”号表示回复力的方向与偏离平衡位置的位移的方向相反.
4.简谐运动的加速度
由F=-kx及牛顿第二定律F=ma可知:a=- x,加速度a与位移x的大小成正比,方向与位移方向相反.
5.物体做简谐运动的判断方法
(1)简谐运动的回复力满足F=-kx;
(2)简谐运动的振动图象是正弦曲线.
例1 (多选)如图4所示,弹簧振子在光滑水平杆上的A、B之间做往复运动,下列说法正确的是
A.弹簧振子运动过程中受重力、支持力和弹簧弹力的
作用
B.弹簧振子运动过程中受重力、支持力、弹簧弹力和回复力的作用
C.振子由A向O运动过程中,回复力逐渐增大
D.从A向O运动的过程中加速度方向向右,逐渐减小
图4
√
√
解析 弹簧振子运动过程中受重力、支持力和弹簧弹力,回复力是根据效果命名的力,它是由物体受到的具体的力所提供的,在此情景中弹簧的弹力充当回复力,故A正确,B错误;
回复力与位移的大小成正比,由A向O运动过程中位移的大小在减小,故此过程回复力逐渐减小,C错误;
加速度方向与位移方向相反,故从A向O运动的过程中加速度方向向右,且A点加速度最大,O点加速度为0,故加速度逐渐减小,故D正确.
例2 在光滑水平面上做简谐运动的弹簧振子的质量是2 kg,当它运动到平衡位置左侧2 cm时,受到的回复力是4 N,当它运动到平衡位置右侧4 cm时,它的加速度是
A.2 m/s2,方向水平向右 B.2 m/s2,方向水平向左
C.4 m/s2,方向水平向右 D.4 m/s2,方向水平向左
√
解析 设向右为正方向,当弹簧振子运动到平衡位置左侧2 cm时,回复力为F1=-kx1,x1=-2 cm,
当它运动到平衡位置右侧4 cm时,回复力为F2=-kx2,x2=4 cm,
又F1=4 N,解得F2=-8 N,
即加速度大小为4 m/s2,方向水平向左,选项D正确.
例3 如图5所示,弹簧劲度系数为k,在弹簧下端挂一个重物,质量为m,重物静止.在竖直方向将重物下拉一段距离(没超过弹簧弹性限度),然后无初速度释放,重物在竖直方向上下振动.(不计空气阻力)
(1)试分析重物上下振动回复力的来源;
答案 见解析
图5
解析 重物在竖直方向上下振动过程中,在竖直方向上受到了重力和弹簧弹力的作用,振动的回复力是重力与弹簧弹力的合力.
(2)试证明该重物做简谐运动.
答案 见解析
解析 重物静止时的位置即为振动的平衡位置,
设此时弹簧的伸长量为x0,根据胡克定律和力的平衡有kx0=mg.
设重物振动过程中某一位置偏离平衡位置的位移为x,并取竖直向下为正方向,如图所示,
此时弹簧的形变量为x+x0,弹簧向上的弹力F弹=-k(x+x0),
重物所受合力即回复力F=mg+F弹,联立得F=-kx.
若x>0,则F<0,表示重物在平衡位置下方,回复力向上;
若x<0,则F>0,表示重物在平衡位置上方,回复力向下,回复力F方向总指向平衡位置.
根据重物的受力特点可以判断重物做简谐运动.
二、简谐运动的能量
导学探究 如图6所示为水平弹簧振子,振子在A、B之间往复运动.
(1)从A到B的运动过程中,振子的动能如何变化?弹簧弹性势能如何变化?振动系统的总机械能是否变化?
图6
答案 振子的动能先增大后减小;弹簧的弹性势能先减小后增大;总机械能保持不变
(2)如果把振子振动的振幅增大,振子回到平衡位置的动能是否增大?振动系统的机械能是否增大?
答案 振子回到平衡位置的动能增大;振动系统的机械能增大
(3)实际的振动系统有空气阻力和摩擦阻力,能量是否损失?理想化的弹簧振动系统,忽略空气阻力和摩擦阻力,能量是否损失?
答案 实际的振动系统有能量损失;理想化的弹簧振动系统能量不变.
1.简谐运动中,振动系统的动能和势能相互转化,平衡位置处动能最大,势能最小;最大位移处动能为零,势能最大,但总的机械能不变.
2.简谐运动的机械能由振幅决定,对于同一个振动系统,振幅越大,振动的能量越大.
3.简谐运动是一种无能量损失的振动,所以其振幅保持不变,又称为等幅振动.
知识深化
例4 如图7所示,一水平弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M.
(1)简谐运动的能量取决于_____,振子振动时动能和_____________相互转化,总机械能_____.
图7
振幅
弹簧弹性势能
守恒
解析 简谐运动的能量取决于振幅,振子振动时动能和弹簧弹性势能相互转化,总机械能守恒.
(2)振子在振动过程中,下列说法中正确的是______.
A.振子在平衡位置时,动能最大,弹簧弹性势能最小
B.振子在最大位移处时,弹簧弹性势能最大,动能最小
C.振子在向平衡位置运动时,由于振子振幅减小,故总机械能减小
D.在任意时刻,动能与弹性势能之和保持不变
ABD
解析 振子在平衡位置两侧往复运动,在平衡位置处速度达到最大,动能最大,弹簧弹性势能最小,所以A正确;
在最大位移处速度为零,动能为零,此时弹簧的形变量最大,弹性势能最大,所以B正确;
振幅的大小与振子的位置无关,在任意时刻只有弹簧的弹力做功,所以机械能守恒,所以C错误,D正确.
(3)若振子运动到B处时将一质量为m的物体放到M的上面使它们一起运动,且m和M间无相对滑动,下列说法正确的是____.
A.振幅不变 B.振幅减小
C.最大动能不变 D.最大动能减小
AC
解析 振子运动到B点时速度恰为零,此时放上m,系统的总能量即为此时弹簧储存的弹性势能,由于简谐运动中机械能守恒,所以振幅保持不变,选项A正确,B错误;
由于机械能守恒,所以最大动能不变,选项C正确,D错误.
三、简谐运动中各物理量的变化
1.如图8所示为水平的弹簧振子示意图,下表为振子运动过程中各物理量的变化情况.
图8
位置
A
A→O
O
O→B
B
位移
最大
向左
0
向右
最大
回复力
(加速度)
最大
向右
0
向左
最大
速度
0
向右
最大
向右
0
动能
0
变大
最大
变小
0
势能
最大
变小
最小
变大
最大
总能量
不变
不变
不变
不变
不变
2.说明:(1)简谐运动中的最大位移处,F、a、Ep最大,Ek=0;在平衡位置处,F=0,a=0,Ep=0,Ek最大.
(2)位移增大时,回复力、加速度和势能增大,速度和动能减小;位移减小时,回复力、加速度和势能减小,速度和动能增大.
(3)位移与回复力(加速度)反向,速度方向则根据位移的变化及具体运动过程判断,各矢量均在其值为零时改变方向.
例5 (2020·金华市十校高二上学期期末联考)如图9甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.取向右为正方向,振子的位移x与时间t的关系图象如图乙所示,下列说法正确的是
A.t=0.8 s时,振子的速度方向向右
B.t=0.2 s时, 振子在O点右侧6 cm处
C.t=0.4 s和t=1.2 s时,振子的加速度相同
D.从t=0.4 s到t=0.8 s的时间内,振子的动能逐渐增大
图9
√
解析 由题图乙知,t=0.8 s时,图象切线的斜率为负,说明振子的速度为负,即振子的速度方向向左,故A错误.
t=0.4 s到t=0.8 s的时间内,振子的位移减小,正向平衡位置靠近,速度逐渐增大,动能逐渐增大,故D正确.
3 简谐运动的回复力和能量
导学探究 如图2所示为一个水平方向的弹簧振子模型(水平杆光滑),O点为振子的平衡位置,A、O间和B、O间距离都是x.
(1)振子在O点时受到几个力的作用?分别是什么力?
一、简谐运动的回复力
重点探究
图2
(2)振子在A、B点时受到哪些力的作用?
(3)除重力、支持力、弹簧弹力外,振子在O、A、B点还受到回复力的作用吗?回复力有什么特点?
一、简谐运动的回复力
1.定义:
2.特点:
按力的作用效果命名,方向始终指向平衡位置
使振子回到平衡位置的力
3.来源:
回复力可以是弹力,也可以是其它力(包括摩擦力);可以是某一个力,或几个力的合力,或者某个力的分力.
1.回复力
回复力是指将振动的物体拉回到平衡位置的力,回复力为零的位置就是平衡位置.
知识深化
2.回复力的来源
回复力是根据力的作用效果命名的,可能由合力、某个力或某个力的分力提供.它一定等于振动物体在振动方向上所受的合力,例如:如图3甲所示,水平方向的弹簧振子,弹力充当回复力;如图乙所示,竖直方向的弹簧振子,弹力和重力的合力充当回复力;如图丙所示,m随M一起振动,m的回复力由静摩擦力提供.
图3
3.回复力公式:F=-kx
(1)k是比例系数,其数值由振动系统决定,与振幅无关.对于水平弹簧振子,回复力仅由弹力提供,k为劲度系数.
(2)“-”号表示回复力的方向与偏离平衡位置的位移的方向相反.
4.简谐运动的加速度
由F=-kx及牛顿第二定律F=ma可知:a=- x,加速度a与位移x的大小成正比,方向与位移方向相反.
5.物体做简谐运动的判断方法
(1)简谐运动的回复力满足F=-kx;
(2)简谐运动的振动图象是正弦曲线.
例1 (多选)如图4所示,弹簧振子在光滑水平杆上的A、B之间做往复运动,下列说法正确的是
A.弹簧振子运动过程中受重力、支持力和弹簧弹力的
作用
B.弹簧振子运动过程中受重力、支持力、弹簧弹力和回复力的作用
C.振子由A向O运动过程中,回复力逐渐增大
D.从A向O运动的过程中加速度方向向右,逐渐减小
图4
√
√
解析 弹簧振子运动过程中受重力、支持力和弹簧弹力,回复力是根据效果命名的力,它是由物体受到的具体的力所提供的,在此情景中弹簧的弹力充当回复力,故A正确,B错误;
回复力与位移的大小成正比,由A向O运动过程中位移的大小在减小,故此过程回复力逐渐减小,C错误;
加速度方向与位移方向相反,故从A向O运动的过程中加速度方向向右,且A点加速度最大,O点加速度为0,故加速度逐渐减小,故D正确.
例2 在光滑水平面上做简谐运动的弹簧振子的质量是2 kg,当它运动到平衡位置左侧2 cm时,受到的回复力是4 N,当它运动到平衡位置右侧4 cm时,它的加速度是
A.2 m/s2,方向水平向右 B.2 m/s2,方向水平向左
C.4 m/s2,方向水平向右 D.4 m/s2,方向水平向左
√
解析 设向右为正方向,当弹簧振子运动到平衡位置左侧2 cm时,回复力为F1=-kx1,x1=-2 cm,
当它运动到平衡位置右侧4 cm时,回复力为F2=-kx2,x2=4 cm,
又F1=4 N,解得F2=-8 N,
即加速度大小为4 m/s2,方向水平向左,选项D正确.
例3 如图5所示,弹簧劲度系数为k,在弹簧下端挂一个重物,质量为m,重物静止.在竖直方向将重物下拉一段距离(没超过弹簧弹性限度),然后无初速度释放,重物在竖直方向上下振动.(不计空气阻力)
(1)试分析重物上下振动回复力的来源;
答案 见解析
图5
解析 重物在竖直方向上下振动过程中,在竖直方向上受到了重力和弹簧弹力的作用,振动的回复力是重力与弹簧弹力的合力.
(2)试证明该重物做简谐运动.
答案 见解析
解析 重物静止时的位置即为振动的平衡位置,
设此时弹簧的伸长量为x0,根据胡克定律和力的平衡有kx0=mg.
设重物振动过程中某一位置偏离平衡位置的位移为x,并取竖直向下为正方向,如图所示,
此时弹簧的形变量为x+x0,弹簧向上的弹力F弹=-k(x+x0),
重物所受合力即回复力F=mg+F弹,联立得F=-kx.
若x>0,则F<0,表示重物在平衡位置下方,回复力向上;
若x<0,则F>0,表示重物在平衡位置上方,回复力向下,回复力F方向总指向平衡位置.
根据重物的受力特点可以判断重物做简谐运动.
二、简谐运动的能量
导学探究 如图6所示为水平弹簧振子,振子在A、B之间往复运动.
(1)从A到B的运动过程中,振子的动能如何变化?弹簧弹性势能如何变化?振动系统的总机械能是否变化?
图6
答案 振子的动能先增大后减小;弹簧的弹性势能先减小后增大;总机械能保持不变
(2)如果把振子振动的振幅增大,振子回到平衡位置的动能是否增大?振动系统的机械能是否增大?
答案 振子回到平衡位置的动能增大;振动系统的机械能增大
(3)实际的振动系统有空气阻力和摩擦阻力,能量是否损失?理想化的弹簧振动系统,忽略空气阻力和摩擦阻力,能量是否损失?
答案 实际的振动系统有能量损失;理想化的弹簧振动系统能量不变.
1.简谐运动中,振动系统的动能和势能相互转化,平衡位置处动能最大,势能最小;最大位移处动能为零,势能最大,但总的机械能不变.
2.简谐运动的机械能由振幅决定,对于同一个振动系统,振幅越大,振动的能量越大.
3.简谐运动是一种无能量损失的振动,所以其振幅保持不变,又称为等幅振动.
知识深化
例4 如图7所示,一水平弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M.
(1)简谐运动的能量取决于_____,振子振动时动能和_____________相互转化,总机械能_____.
图7
振幅
弹簧弹性势能
守恒
解析 简谐运动的能量取决于振幅,振子振动时动能和弹簧弹性势能相互转化,总机械能守恒.
(2)振子在振动过程中,下列说法中正确的是______.
A.振子在平衡位置时,动能最大,弹簧弹性势能最小
B.振子在最大位移处时,弹簧弹性势能最大,动能最小
C.振子在向平衡位置运动时,由于振子振幅减小,故总机械能减小
D.在任意时刻,动能与弹性势能之和保持不变
ABD
解析 振子在平衡位置两侧往复运动,在平衡位置处速度达到最大,动能最大,弹簧弹性势能最小,所以A正确;
在最大位移处速度为零,动能为零,此时弹簧的形变量最大,弹性势能最大,所以B正确;
振幅的大小与振子的位置无关,在任意时刻只有弹簧的弹力做功,所以机械能守恒,所以C错误,D正确.
(3)若振子运动到B处时将一质量为m的物体放到M的上面使它们一起运动,且m和M间无相对滑动,下列说法正确的是____.
A.振幅不变 B.振幅减小
C.最大动能不变 D.最大动能减小
AC
解析 振子运动到B点时速度恰为零,此时放上m,系统的总能量即为此时弹簧储存的弹性势能,由于简谐运动中机械能守恒,所以振幅保持不变,选项A正确,B错误;
由于机械能守恒,所以最大动能不变,选项C正确,D错误.
三、简谐运动中各物理量的变化
1.如图8所示为水平的弹簧振子示意图,下表为振子运动过程中各物理量的变化情况.
图8
位置
A
A→O
O
O→B
B
位移
最大
向左
0
向右
最大
回复力
(加速度)
最大
向右
0
向左
最大
速度
0
向右
最大
向右
0
动能
0
变大
最大
变小
0
势能
最大
变小
最小
变大
最大
总能量
不变
不变
不变
不变
不变
2.说明:(1)简谐运动中的最大位移处,F、a、Ep最大,Ek=0;在平衡位置处,F=0,a=0,Ep=0,Ek最大.
(2)位移增大时,回复力、加速度和势能增大,速度和动能减小;位移减小时,回复力、加速度和势能减小,速度和动能增大.
(3)位移与回复力(加速度)反向,速度方向则根据位移的变化及具体运动过程判断,各矢量均在其值为零时改变方向.
例5 (2020·金华市十校高二上学期期末联考)如图9甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动.取向右为正方向,振子的位移x与时间t的关系图象如图乙所示,下列说法正确的是
A.t=0.8 s时,振子的速度方向向右
B.t=0.2 s时, 振子在O点右侧6 cm处
C.t=0.4 s和t=1.2 s时,振子的加速度相同
D.从t=0.4 s到t=0.8 s的时间内,振子的动能逐渐增大
图9
√
解析 由题图乙知,t=0.8 s时,图象切线的斜率为负,说明振子的速度为负,即振子的速度方向向左,故A错误.
t=0.4 s到t=0.8 s的时间内,振子的位移减小,正向平衡位置靠近,速度逐渐增大,动能逐渐增大,故D正确.
