《矩阵专题复习》(新人教A版选修4-2)
文档属性
| 名称 | 《矩阵专题复习》(新人教A版选修4-2) |

|
|
| 格式 | rar | ||
| 文件大小 | 352.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-12 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
《选修4-2矩阵专题复习》
1、矩阵的计算
(1)矩阵与向量的乘法:
2、各种变换:
(1)恒等变换: (4)反射变换
(2)伸压变换: (5)投影变换
(3)旋转变换: (6)切变变换
一、知识要点梳理
一、知识要点梳理
3、逆矩阵与二阶行列式
(1)逆矩阵定义:
(2)几何意义:如
(3)定理: 设
若A可逆 ,此时
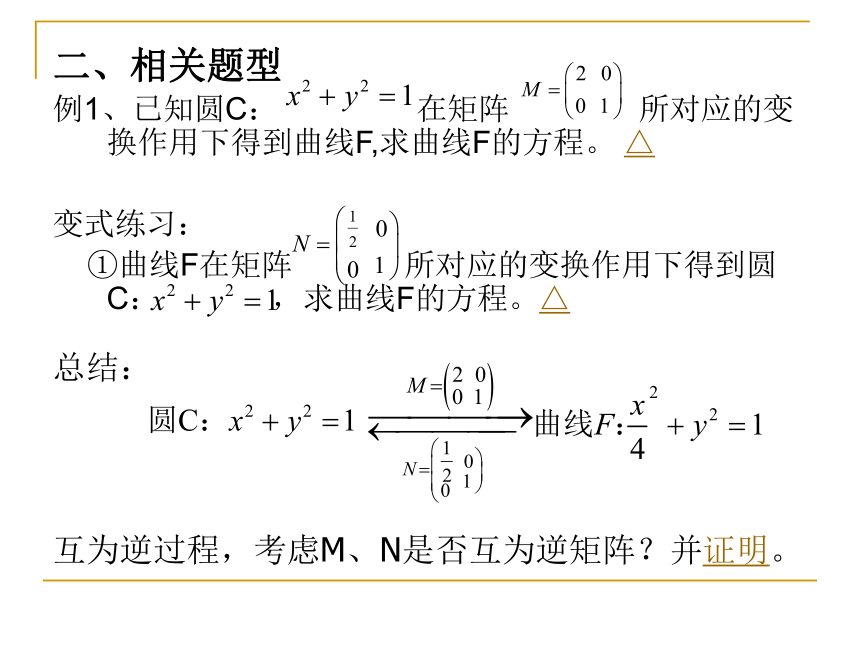
总结:
互为逆过程,考虑M、N是否互为逆矩阵?并证明。
例1、已知圆C: 在矩阵 所对应的变换作用下得到曲线F,求曲线F的方程。 △
变式练习:
①曲线F在矩阵 所对应的变换作用下得到圆C: ,求曲线F的方程。△
二、相关题型
二、相关题型
例1、已知圆C: 在矩阵 所对应的变换作用下得到曲线F,求曲线F的方程。 △
变式练习:
①曲线F在矩阵 所对应的变换作用下得到圆C: ,求曲线F的方程。△
②若直线 矩阵 所表示的变换作用下得到另一直线 ,求 的值
△△△
变式练习:
③已知曲线C: 在矩阵 所对应的变换作用下得到曲线 ,且曲线 绕原点逆时针旋转 得到曲线F,求曲线F的方程。 △
变式练习:
③已知曲线C: 在矩阵 所对应的变换作用下得到曲线 ,且曲线 绕原点逆时针旋转 得到曲线F,求曲线F的方程。
10年市质检卷第21(1)题
10年市质检卷第21(1)题
10年市质检卷第21(1)题
10年市质检卷第21(1)题
10年市质检卷第21(1)题
下面解法同解法二
三、作业布置
1、已知椭圆:
在矩阵
变换作用下得到曲线F,求曲线F的方程。
所对应的
得到椭圆C:
2、已知曲线F在矩阵
所对应的变换作用下
,求曲线F的方程。
3、若直线
在矩阵
换作用下得到直线
,求
的值
所表示的变
4、已知曲线
绕原点逆时针旋转
得到
曲线 ,且曲线 在矩阵
变换作用下得到曲线F,求曲线F的方程。
所对应的
谢谢!
二、相关题型
例1、已知圆C: 在矩阵 所对
应的变换作用下得到曲线F,求曲线F的方程。
则
返回
①曲线F在矩阵 所对应的变换作用下得到圆C: ,求曲线F的方程。
巩固练习:
返回
返回
②若直线 在矩阵 所表示的变换作用下得到另一直线 ,求 的值
②若直线 在矩阵 所表示的变换作用下得到另一直线 ,求 的值
返回
②若直线 在矩阵 所表示的变换作用下得到另一直线 ,求 的值
②若直线 在矩阵 所表示的变换作用下得到另一直线 ,求 的值
返回
变式练习:
③已知曲线C: 在矩阵 所对应的变换作用下得到曲线 ,且曲线 绕原点逆时针旋转 得到曲线F,求曲线F的方程。
变式练习:
③已知曲线C: 在矩阵 所对应的变换作用下得到曲线 ,且曲线 绕原点逆时针旋转 得到曲线F,求曲线F的方程。
返回
《选修4-2矩阵专题复习》
1、矩阵的计算
(1)矩阵与向量的乘法:
2、各种变换:
(1)恒等变换: (4)反射变换
(2)伸压变换: (5)投影变换
(3)旋转变换: (6)切变变换
一、知识要点梳理
一、知识要点梳理
3、逆矩阵与二阶行列式
(1)逆矩阵定义:
(2)几何意义:如
(3)定理: 设
若A可逆 ,此时
总结:
互为逆过程,考虑M、N是否互为逆矩阵?并证明。
例1、已知圆C: 在矩阵 所对应的变换作用下得到曲线F,求曲线F的方程。 △
变式练习:
①曲线F在矩阵 所对应的变换作用下得到圆C: ,求曲线F的方程。△
二、相关题型
二、相关题型
例1、已知圆C: 在矩阵 所对应的变换作用下得到曲线F,求曲线F的方程。 △
变式练习:
①曲线F在矩阵 所对应的变换作用下得到圆C: ,求曲线F的方程。△
②若直线 矩阵 所表示的变换作用下得到另一直线 ,求 的值
△△△
变式练习:
③已知曲线C: 在矩阵 所对应的变换作用下得到曲线 ,且曲线 绕原点逆时针旋转 得到曲线F,求曲线F的方程。 △
变式练习:
③已知曲线C: 在矩阵 所对应的变换作用下得到曲线 ,且曲线 绕原点逆时针旋转 得到曲线F,求曲线F的方程。
10年市质检卷第21(1)题
10年市质检卷第21(1)题
10年市质检卷第21(1)题
10年市质检卷第21(1)题
10年市质检卷第21(1)题
下面解法同解法二
三、作业布置
1、已知椭圆:
在矩阵
变换作用下得到曲线F,求曲线F的方程。
所对应的
得到椭圆C:
2、已知曲线F在矩阵
所对应的变换作用下
,求曲线F的方程。
3、若直线
在矩阵
换作用下得到直线
,求
的值
所表示的变
4、已知曲线
绕原点逆时针旋转
得到
曲线 ,且曲线 在矩阵
变换作用下得到曲线F,求曲线F的方程。
所对应的
谢谢!
二、相关题型
例1、已知圆C: 在矩阵 所对
应的变换作用下得到曲线F,求曲线F的方程。
则
返回
①曲线F在矩阵 所对应的变换作用下得到圆C: ,求曲线F的方程。
巩固练习:
返回
返回
②若直线 在矩阵 所表示的变换作用下得到另一直线 ,求 的值
②若直线 在矩阵 所表示的变换作用下得到另一直线 ,求 的值
返回
②若直线 在矩阵 所表示的变换作用下得到另一直线 ,求 的值
②若直线 在矩阵 所表示的变换作用下得到另一直线 ,求 的值
返回
变式练习:
③已知曲线C: 在矩阵 所对应的变换作用下得到曲线 ,且曲线 绕原点逆时针旋转 得到曲线F,求曲线F的方程。
变式练习:
③已知曲线C: 在矩阵 所对应的变换作用下得到曲线 ,且曲线 绕原点逆时针旋转 得到曲线F,求曲线F的方程。
返回
