2020-2021学年人教版八年级数学下册第18章《平行四边形》单元综合课后提升训练(word版,含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册第18章《平行四边形》单元综合课后提升训练(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 482.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 08:06:42 | ||
图片预览




文档简介
2021年人教版版 八年级数学下册第18章平行四边形单元综合课后提升训练(附答案)
1.如图,两把完全一样的直尺叠放在﹣起,重合的部分构成一个四边形,给出以下四个论断:①这个四边形可能是正方形②这个四边形一定是菱形③这个四边形不可能是矩形④这个四边形一定是轴对称图形,其中正确的论断是( )
A.①② B.③④ C.①②④ D.①②③④
2.下列条件中,不能判定一个四边形是菱形的是( )
A.一组邻边相等的平行四边形
B.一条对角线平分一组对角的四边形
C.四条边都相等的四边形
D.对角线互相垂直平分的四边形
3.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
A. B. C. D.
4.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
5.在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为( )
A.28或32 B.28或36 C.32或36 D.28或32或36
6.如图,平行四边形ABCD中,AB=3,BC=5.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )
A. B. C.1 D.2
7.将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,),则点C的坐标是( )
A.(4,2) B.(2,4) C.(,3) D.(3,)
8.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
9.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )
A.120° B.130° C.140° D.150°
10.如图,?ABCD的对角线AC与BD相交于点O,AC⊥BC,且AB=10,AD=6,则OB的长度为( )
A.2 B.4 C.8 D.4
11.已知四边形ABCD,给出下列条件:①AB∥CD;②BC∥AD;③AB=CD;④∠A=∠C;从中任取两个条件,可以得出四边形ABCD是平行四边形这一结论的情况有( )
A.5种 B.4种 C.3种 D.2种
12.如果一个直角三角形的两边分别是6,8,那么斜边上的中线长为( )
A.4 B.5 C.3或5 D.4或5
13.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.则四边形AODE一定是( )
A.正方形 B.菱形 C.矩形 D.不能确定
14.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为( )
A. B. C. D.
15.如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④AD2+AE2=4AG2.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
16.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
17.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=,AB=3,给出下列结论:①∠COD=45°,②AE=5,③CF=BD=,④△COF的面积S△COF=3,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
18.如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A. B. C. D.
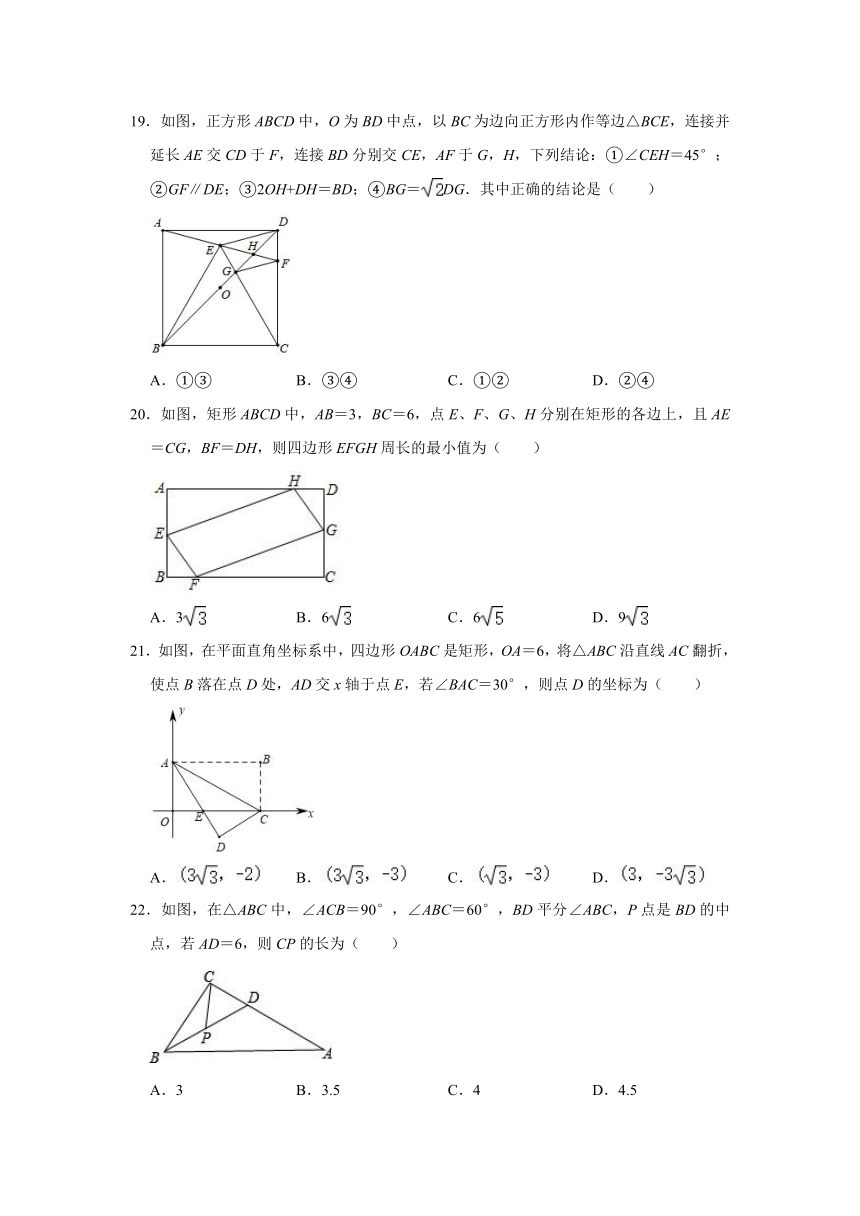
19.如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G,H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=DG.其中正确的结论是( )
A.①③ B.③④ C.①② D.②④
20.如图,矩形ABCD中,AB=3,BC=6,点E、F、G、H分别在矩形的各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
A.3 B.6 C.6 D.9
21.如图,在平面直角坐标系中,四边形OABC是矩形,OA=6,将△ABC沿直线AC翻折,使点B落在点D处,AD交x轴于点E,若∠BAC=30°,则点D的坐标为( )
A. B. C. D.
22.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为( )
A.3 B.3.5 C.4 D.4.5
23.如图,在?ABCD中,AC与BD交于点O,下列判断中不正确的是( )
A.若AB=BC,则?ABCD是菱形
B.若AC⊥BD,则?ABCD是菱形
C.若AC平分∠BAD,则?ABCD是菱形
D.若AC=BD,则?ABCD是菱形
24.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,
则PE+PF的值是 cm.
25.如图,在△ABC中,AB=AC,BC=6,AF⊥BC于点F,BE⊥AC于点E,且点D是AB的中点,△DEF的周长是11,则AB= .
26.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
27.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.
28.如图,在四边形ABCD中,E是BC上一点,AE交BD于点O,AD=BD,∠ADB=∠EDC,DE=DC.
(1)求证:△ADE≌△BDC;
(2)若∠AEB=36°,求∠EDC;
(3)若OB=OE,求证:四边形ABCD是平行四边形.
29.如图,平行四边形ABCD的对角线AC、BD交于点O,分别过点C、D作CF∥BD,DF∥AC,连接BF交AC于点E.
(1)求证:△FCE≌△BOE;
(2)当△ADC满足什么条件时,四边形OCFD为菱形?请说明理由.
30.在△ABC中,∠BAC=90°,AD是BC边上的中线,点E为AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)①当∠ACB等于多少度时,四边形ADCF为正方形;
②连接DF,当∠ACB等于多少度时,四边形ABDF为菱形.
31.如图,AM∥BN,C是BN上一点,BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.
(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE=AB=2,求菱形ABCD的面积.
32.如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD.
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,AC=,CD=BD,求AD的长.
33.如图,过△ABC边AC的中点O,作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD,CE,若CE平分∠ACB,CE⊥BO于点F.
(1)求证:①OC=BC;
②四边形ABCD是矩形;
(2)若BC=3,求DE的长.
34.如图,在△ABC中,AB=12cm,AC=8cm,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长.
35.如图,在四边ABCD中,AB∥DC,AB=AD,对角AC、BD交于O,AC平分∠BAD.
(1)求证:四边形ABCD是菱形;
(2)过点C作CE⊥AB交AB的延长线于点E,连接OE,若AB=2,BD=4,求OE的长.
36.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
37.(1)如图1的正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=FG;
(2)如图2,等腰Rt△ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,求MN的长.
38.如图,在Rt△ABC中,∠ACB=90°.CD⊥AB,AF平分∠CAB,交CD于点E,交BC于点F.过点F作FG⊥AB交AB于点G,连接EG.
(1)求证:四边形CEGF是菱形;
(2)若∠B=30°,AC=6,求CE的长.
39.如图,四边形ABCD的对角线AC⊥BD于点E,点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.
(1)求证:四边形DBFC是菱形;
(2)若AB=BC,∠F=45°,BD=2,求AC的长.
参考答案
1.解:过点D作DE⊥AB于E,DF⊥BC于F.
∵两张长方形直尺的宽度相等,
∴DE=DF,
又∵平行四边形ABCD的面积=AB?DE=BC?DF,
∴AB=BC,
∴平行四边形ABCD为菱形.
当∠DAB=90°时,这个四边形是正方形,
∴这个四边形一定是轴对称图形,
故选:C.
2.解:A、∵一组邻边相等的平行四边形是菱形,
∴选项A不符合题意;
B、∵一条对角线平分一组对角的四边形不一定是菱形,
∴选项B符合题意;
C、∵四边相等的四边形是菱形,
∴选项C不符合题意;
D、∵对角线互相垂直平分的四边形是菱形,
∴选项D不符合题意;
故选:B.
3.解:∵四边形为矩形,
∴OB=OD=OA=OC,
在△EBO与△FDO中,
∵,
∴△EBO≌△FDO(ASA),
∴阴影部分的面积=S△AEO+S△EBO=S△AOB,
∵△AOB与△ABC同底且△AOB的高是△ABC高的,
∴S△AOB=S△OBC=S矩形ABCD.
故选:B.
4.解:A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;
B、对角线互相垂直的平行四边形是菱形;故本选项错误;
C、对角线互相平分的四边形是平行四边形;故本选项正确;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误;
故选:C.
5.解:∵∠C=90°,AC=6,BC=8,
∴AB==10,
若以AC,BC为边,则平行四边形的周长=2(AC+BC)=2×(6+8)=28,
若以AC,AB为边,则平行四边形的周长=2(AC+AB)=2×(6+10)=32,
若以AB,BC为边,则平行四边形的周长=2(AB+BC)=2×(10+8)=36,
故选:D.
6.解:∵由题意可知CE是∠BCD的平分线,
∴∠BCE=∠DCE.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DCE=∠E,
∴∠BCE=∠AEC,
∴BE=BC=5,
∵AB=3,
∴AE=BE﹣AB=2,
故选:D.
7.解:如图:过点A作AE⊥x轴于点E,过点B作BF⊥⊥x轴于点F,过点A作AN⊥BF于点N,
过点C作CM⊥x轴于点M,
∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,
∴∠EAO=∠COM,
又∵∠AEO=∠CMO,
∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,
∴∠BAN=∠EAO=∠COM,
在△ABN和△OCM中
,
∴△ABN≌△OCM(AAS),
∴BN=CM,
∵点A(﹣1,2),点B的纵坐标是,
∴BN=,
∴CM=,
∴MO=3,
∴点C的坐标是:(3,).
故选:D.
8.解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A错误;
若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;
若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;
若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.
9.解:∵四边形ABCD是菱形,
∴OB=OD,AC⊥BD,∠ADC=∠ABC,
∵DH⊥AB,
∴OH=OB=BD,
∵∠DHO=20°,
∴∠OHB=90°﹣∠DHO=70°,
∴∠ABD=∠OHB=70°,
∴∠ADC=∠ABC=2∠ABD=140°,
故选:C.
10.解:∵四边形ABCD是平行四边形,
∴BC=AD=6,OA=OC,
∵AC⊥BC,AB=10,
∴==8,
∴AO=CO=AC=4,
∴OB===2;
故选:A.
11.
解:如图 ①AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形;
②∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边;
③∵AB∥CD,∴∠B+∠C=180°,
∵∠A=∠C,∴∠B+∠A=180°,
∴AD∥BC,
∴四边形ABCD是平行四边;
④∵BC∥AD,∴∠B+∠A=180°,
∵∠A=∠C,∴∠B+∠C=180°,
∴AB∥CD,
∴四边形ABCD是平行四边;
故选:B.
12.解:当一个直角三角形的两直角边分别是6,8时,
由勾股定理得,斜边==10,
则斜边上的中线=×10=5,
当8是斜边时,斜边上的中线是4,
故选:D.
13.解:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=∠AOD=90°,
∴四边形AODE是矩形,
故选:C.
14.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,∠EDO=∠FBO,
∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,
∴BO=DO,EF⊥BD,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∵BO=DO,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形,
∴BE=DE,
∵AB=5,AD=12,∠A=90°,
∴BD=13,
设DE=x,则AE=12﹣x,
在Rt△AEB中,AB2+AE2=BE2,
即52+(12﹣x)2=x2,
∴x=,
∴BE=DE=,
在Rt△BEO中,OE=,
∴EF=2EO=,
∴菱形BEDF的面积=,
故选:A.
15.解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=DE,AG=CG,DG=EG,
∴DG=AG=CG=EG,
在Rt△AED中,AD2+AE2=DE2=AC2=(2AG)2=4AG2,故④正确;
∵AE=BD=BC,AG=AC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
16.解:分两种情况讨论:
①当E点在线段DC上时,
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵,AD'=AD,
∴BE=AB=10,
∵,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上时,如下图,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵,
∴DE=D″E=BD''+BE=8+10=18.
综上所知,DE=2或18.
故选:D.
17.解:①∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,
故正确;
②∵EF=,
∴OE=2,
∵AO=AB=3,
∴AE=AO+OE=2+3=5,
故正确;
③作DH⊥AB于H,作FG⊥CO交CO的延长线于G,
则FG=1,
CF=,
BH=3﹣1=2,
DH=3+1=4,
BD=,
故错误;
④△COF的面积S△COF=×3×1=,
故错误;
故选:B.
18.解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADB=∠ADC=60°,
∴△ABD是等边三角形,
∴AD=BD,
又∵△DEF是等边三角形,
∴∠EDF=∠DEF=60°,
又∵∠ADB=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,,
∴△ADE≌△BDF(ASA),
∴AE=BF,
∵AE=t,CF=2t,
∴BF=BC﹣CF=5﹣2t,
∴t=5﹣2t
∴t=,
故选:D.
19.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠ADB=∠CDB=45°.
∵△BEC是等边三角形,
∴BC=BE=CE,∠EBC=∠BCE=∠BEC=60°,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴∠BAE=∠BEA=∠CED=∠CDE=75°,
∴∠EAD=∠EDA=15°,
∴∠DEF=30°,
∴∠CEF=45°.故①正确;
②∵∠EDC=75°,∠BDC=45°,
∴∠EDB=30°,
∴∠DEF=∠EDG.∠EGD=75°.
∵∠ADC=90°,∠DAF=15°,
∴∠EFD=75°,
∴∠EFD=∠EGD.
在△DEF和△EDG中,
,
∴△DEF≌△EDG(AAS),
∴DF=EG.
∵EC=DC,
∴EC﹣EG=DC﹣DF,
∴CG=CF,
∴∠CGF=∠CFG=75°,
∴∠CED=∠CGF,
∴GF∥ED.故②正确;
③由图可知2(OH+HD)=2OD=BD,所以2OH+DH=BD此结论不正确;
④作BM⊥CG于M,DN⊥CG于N,
∴∠BMC=∠DNC=90°,
设AB=BC=CD=AD=x,
∴BM=x,DN=x.
∵,
∴=,
∴BG=DG.故④错误;
故选:C.
20.解:作点E关于BC的对称点E′,连接E′G交BC于点F,此时四边形EFGH周长取最小值,EF=E'F,
过点G作GG′⊥AB于点G′,如图所示.
∵AE=CG,BE=BE′,
∴E′G′=AB=3,
∵GG′=AD=6,
∴E′G===3,
∴C四边形EFGH=2(GF+EF)=2E′G=6.
故选:C.
21.解:过D点作DF⊥x轴,垂足为F,则DF∥y轴,
∵四边形AOCB为矩形,
∴∠OAB=∠AOC=∠B=90°,BC=AO=6,AB=OC,
∵∠BAC=30°,
∴AC=12,OC=AB=,
由折叠可知:∠DAC=∠BAC=30°,AD=AB=,
∴∠OAE=30°,
∴OE=,AE=,
∴ED=,
∵DF∥y轴,
∴∠EDF=∠EAO=30°,
∴EF=,DF=3,
∴OF=OE+EF=,
∴D点坐标为(,﹣3),
故选:B.
22.解:∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC,
∴∠CBD=∠DBA=30°,
∴BD=AD,
∵AD=6,
∴BD=6,
∵P点是BD的中点,
∴CP=BD=3.
故选:A.
23.解:A、由一组邻边相等的平行四边形是菱形可判断?ABCD是菱形;
B、对角线互相垂直的平行四边形是菱形可判断?ABCD是菱形;
C、由AC平分∠BAD,可得四边相等,即可判断?ABCD是菱形;
D、由对角线相等的平行四边形是矩形,可判断?ABCD是矩形.
故选:D.
24.解:连接BP,
(cm2),
∴AB=BC==3(cm),
∴(cm2),
∴,
∴(cm),
故答案为:2.
25.解:∵AF⊥BC,BE⊥AC,D是AB的中点,
∴DE=DF=AB,
∵AB=AC,AF⊥BC,
∴点F是BC的中点,∴BF=FC=3,
∵BE⊥AC,
∴EF=BC=3,
∴△DEF的周长=DE+DF+EF=AB+3=11,
∴AB=8,
故答案为:8.
26.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∵在△ABC和△AED中,
,
∴△ABC≌△EAD.
(2)解:∵AE平分∠DAB(已知),
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°.
∵△ABC≌△EAD,
∴∠AED=∠BAC=85°.
27.证明:(1)∵AF∥BC,
∴∠AFE=∠DBE
∵△ABC是直角三角形,AD是BC边上的中线,E是AD的中点,
∴AE=DE,BD=CD
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS))
∴AF=BD
(2)由(1)知,AF=BD,且BD=CD,
∴AF=CD,且AF∥BC,
∴四边形ADCF是平行四边形
∵∠BAC=90°,D是BC的中点,
∴
∴四边形ADCF是菱形
28.(1)证明:∵∠ADB=∠EDC,
∴∠ADE=∠BDC,
在△ADE和△BDC中,,
∴△ADE≌△BDC(SAS);
(2)解:∵△ADE≌△BDC,
∴∠AED=∠C,
∵∠AEB=36°,
∴∠AED=∠DEC=∠C=(180°﹣36°)=72°,
∴∠EDC=180°﹣2×72°=36°;
(3)证明:∵OB=OE,
∴∠OBE=∠OEB,
∵∠DAE=∠OBE,
∴∠OEB=∠DAE,
∴AD∥BC,
∴∠ADB=∠OBE,
∴∠ADB=∠DAE,
∴OA=OD,
∴AE=BD,
∵AD=BD,
∴AE=AD,
∵△ADE≌△BDC,
∴AE=BC,
∴AD=BC,
∴四边形ABCD是平行四边形.
29.(1)证明:∵CF∥BD,DF∥AC,
∴四边形OCFD是平行四边形,∠OBE=∠CFE,
∴OD=CF,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OB=CF,在
△FCE和△BOE中,,
∴△FCE≌△BOE(AAS);
(2)解:当△ADC满足∠ADC=90°时,四边形OCFD为菱形;理由如下:
∵∠ADC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OC=OD,
∴四边形OCFD为菱形.
30.(1)证明:∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)解:①当∠ACB=45°时,四边形ADCF为正方形;
∵AD=AF,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是菱形,
∴∠ACD=∠ACF=45°,
∴∠DCF=90°,
∴四边形ADCF是正方形;
②当∠ACB=30°时,四边形ABDF为菱形;
∵四边形ADCF是菱形,四边形ABDF是平行四边形,
∴CD=CF,
∵∠ACB=∠ACF=30°,
∴∠DCF=60°,
∴△DCF是等边三角形,
∴DF=CD,
∴DF=BD,
∴四边形ABDF为菱形.
故答案为:45,30.
31.解:(1)证明:∵点O是AC的中点,
∴AO=CO,
∵AM∥BN,
∴∠DAC=∠ACB,
在△AOD和△COB中,,
∴△ADO≌△CBO(ASA);
(2)证明:由(1)得△ADO≌△CBO,
∴AD=CB,
又∵AM∥BN,
∴四边形ABCD是平行四边形,
∵AM∥BN,
∴∠ADB=∠CBD,
∵BD平分∠ABN,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AD=AB,
∴平行四边形ABCD是菱形;
(3)解:由(2)得四边形ABCD是菱形,
∴AC⊥BD,AD=CB,
又DE⊥BD,
∴AC∥DE,
∵AM∥BN,
∴四边形ACED是平行四边形,
∴AC=DE=2,AD=EC,
∴EC=CB,
∵四边形ABCD是菱形,
∴EC=CB=AB=2,
∴EB=4,
在Rt△DEB中,由勾股定理得BD==,
∴.
32.(1)证明:∵AB∥CE,
∴∠CAD=∠ACE,∠ADE=∠CED.
∵F是AC中点,
∴AF=CF.
在△AFD与△CFE中,
.
∴△AFD≌△CFE(AAS),
∴AD=CE,
∴四边形ADCE是平行四边形;
(2)解:过点C作CG⊥AB于点G.
∵CD=BD,∠B=30°,
∴∠DCB=∠B=30°,
∴∠CDA=60°.
在△ACG中,∠AGC=90°,,∠CAG=45°,
∴.
在△CGD中,∠DGC=90°,∠CDG=60°,,
∴GD=1,
∴.
33.(1)证明:①∵CE平分∠ACB,
∴∠OCE=∠BCE,
∵BO⊥CE,
∴∠CFO=∠CFB=90°,
在△OCF与△BCF中,
,
∴△OCF≌△BCF(ASA),
∴OC=BC;
②∵点O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
在△OAD与△OCB中,
,
∴△OAD≌△OCB(ASA),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵OE⊥AC,
∴∠EOC=90°,
在△OCE与△BCE中,
,
∴△OCE≌△BCE(SAS),
∴∠EBC=∠EOC=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AD=BC=3,∠DAB=90°,AC=BD,
∴OB=OC,
∵OC=BC,
∴OC=OB=BC,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠ECB=OCB=30°,
∵∠EBC=90°,
∴EB=EC,
∵BE2+BC2=EC2,BC=3,
∴EB=,EC=2,
∵OE⊥AC,OA=OC,
∴EC=EA=2,
在Rt△ADE中,∠DAB=90°,
∴DE===.
34.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA).
∴AG=AC=8cm,
∴GF=CF,则BG=AB﹣AG=12﹣8=4(cm).
又∵BE=CE,
∴EF是△BCG的中位线.
∴EF=BG=2cm.
答:EF的长为2cm,
35.解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=4,
∴OB=BD=2,
在Rt△AOB中,AB=2,OB=2,
∴OA===4,
∴OE=OA=4.
36.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=AB=×4=8,
∴CE+CG=8是定值.
37.(1)证明:在正方形ABCD中,
∠ABE=∠ADG,AD=AB,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∴∠EAG=90°,
在△FAE和△GAF中,
,
∴△FAE≌△GAF(SAS),
∴EF=FG;
(2)解:如图,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.
∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,
,
∴△ABM≌△ACE(SAS).
∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,
,
∴△MAN≌△EAN(SAS).
∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
∴MN2=BM2+NC2.
∵BM=1,CN=3,
∴MN2=12+32,
∴MN=.
38.(1)证明:∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=FG,
在Rt△ACF与Rt△AGF中,,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG,
∵CD⊥AB,FG⊥AB,
∴CD∥FG,
∴∠CEF=∠EFG,
∴∠CEF=∠CFE,
∴CE=CF,
∴CE=FG,
∵CE∥FG,
∴四边形CEGF是平行四边形,
∵CE=CF,
∴平行四边形CEGF菱形;
(2)解:∵Rt△ACF≌Rt△AGF,
∴AG=AC=6,
∵∠B=30°,∠ACB=90°,
∴AB=2AC=2×6=12,
∴BG=AB﹣AG=12﹣6=6,
∴CE=FG=2.
39.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
∵BC平分∠DBF,
∴∠CBF=∠CBD,
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD,
∴四边形DBFC是菱形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
作CM⊥BF于M,如图:
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=,
∴AC=2.
1.如图,两把完全一样的直尺叠放在﹣起,重合的部分构成一个四边形,给出以下四个论断:①这个四边形可能是正方形②这个四边形一定是菱形③这个四边形不可能是矩形④这个四边形一定是轴对称图形,其中正确的论断是( )
A.①② B.③④ C.①②④ D.①②③④
2.下列条件中,不能判定一个四边形是菱形的是( )
A.一组邻边相等的平行四边形
B.一条对角线平分一组对角的四边形
C.四条边都相等的四边形
D.对角线互相垂直平分的四边形
3.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
A. B. C. D.
4.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
5.在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为( )
A.28或32 B.28或36 C.32或36 D.28或32或36
6.如图,平行四边形ABCD中,AB=3,BC=5.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )
A. B. C.1 D.2
7.将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,),则点C的坐标是( )
A.(4,2) B.(2,4) C.(,3) D.(3,)
8.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
9.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )
A.120° B.130° C.140° D.150°
10.如图,?ABCD的对角线AC与BD相交于点O,AC⊥BC,且AB=10,AD=6,则OB的长度为( )
A.2 B.4 C.8 D.4
11.已知四边形ABCD,给出下列条件:①AB∥CD;②BC∥AD;③AB=CD;④∠A=∠C;从中任取两个条件,可以得出四边形ABCD是平行四边形这一结论的情况有( )
A.5种 B.4种 C.3种 D.2种
12.如果一个直角三角形的两边分别是6,8,那么斜边上的中线长为( )
A.4 B.5 C.3或5 D.4或5
13.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.则四边形AODE一定是( )
A.正方形 B.菱形 C.矩形 D.不能确定
14.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为( )
A. B. C. D.
15.如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④AD2+AE2=4AG2.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
16.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
17.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=,AB=3,给出下列结论:①∠COD=45°,②AE=5,③CF=BD=,④△COF的面积S△COF=3,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
18.如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A. B. C. D.
19.如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE,AF于G,H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=DG.其中正确的结论是( )
A.①③ B.③④ C.①② D.②④
20.如图,矩形ABCD中,AB=3,BC=6,点E、F、G、H分别在矩形的各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
A.3 B.6 C.6 D.9
21.如图,在平面直角坐标系中,四边形OABC是矩形,OA=6,将△ABC沿直线AC翻折,使点B落在点D处,AD交x轴于点E,若∠BAC=30°,则点D的坐标为( )
A. B. C. D.
22.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为( )
A.3 B.3.5 C.4 D.4.5
23.如图,在?ABCD中,AC与BD交于点O,下列判断中不正确的是( )
A.若AB=BC,则?ABCD是菱形
B.若AC⊥BD,则?ABCD是菱形
C.若AC平分∠BAD,则?ABCD是菱形
D.若AC=BD,则?ABCD是菱形
24.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,
则PE+PF的值是 cm.
25.如图,在△ABC中,AB=AC,BC=6,AF⊥BC于点F,BE⊥AC于点E,且点D是AB的中点,△DEF的周长是11,则AB= .
26.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
27.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.
28.如图,在四边形ABCD中,E是BC上一点,AE交BD于点O,AD=BD,∠ADB=∠EDC,DE=DC.
(1)求证:△ADE≌△BDC;
(2)若∠AEB=36°,求∠EDC;
(3)若OB=OE,求证:四边形ABCD是平行四边形.
29.如图,平行四边形ABCD的对角线AC、BD交于点O,分别过点C、D作CF∥BD,DF∥AC,连接BF交AC于点E.
(1)求证:△FCE≌△BOE;
(2)当△ADC满足什么条件时,四边形OCFD为菱形?请说明理由.
30.在△ABC中,∠BAC=90°,AD是BC边上的中线,点E为AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)①当∠ACB等于多少度时,四边形ADCF为正方形;
②连接DF,当∠ACB等于多少度时,四边形ABDF为菱形.
31.如图,AM∥BN,C是BN上一点,BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.
(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE=AB=2,求菱形ABCD的面积.
32.如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD.
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,AC=,CD=BD,求AD的长.
33.如图,过△ABC边AC的中点O,作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD,CE,若CE平分∠ACB,CE⊥BO于点F.
(1)求证:①OC=BC;
②四边形ABCD是矩形;
(2)若BC=3,求DE的长.
34.如图,在△ABC中,AB=12cm,AC=8cm,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长.
35.如图,在四边ABCD中,AB∥DC,AB=AD,对角AC、BD交于O,AC平分∠BAD.
(1)求证:四边形ABCD是菱形;
(2)过点C作CE⊥AB交AB的延长线于点E,连接OE,若AB=2,BD=4,求OE的长.
36.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
37.(1)如图1的正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=FG;
(2)如图2,等腰Rt△ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,求MN的长.
38.如图,在Rt△ABC中,∠ACB=90°.CD⊥AB,AF平分∠CAB,交CD于点E,交BC于点F.过点F作FG⊥AB交AB于点G,连接EG.
(1)求证:四边形CEGF是菱形;
(2)若∠B=30°,AC=6,求CE的长.
39.如图,四边形ABCD的对角线AC⊥BD于点E,点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.
(1)求证:四边形DBFC是菱形;
(2)若AB=BC,∠F=45°,BD=2,求AC的长.
参考答案
1.解:过点D作DE⊥AB于E,DF⊥BC于F.
∵两张长方形直尺的宽度相等,
∴DE=DF,
又∵平行四边形ABCD的面积=AB?DE=BC?DF,
∴AB=BC,
∴平行四边形ABCD为菱形.
当∠DAB=90°时,这个四边形是正方形,
∴这个四边形一定是轴对称图形,
故选:C.
2.解:A、∵一组邻边相等的平行四边形是菱形,
∴选项A不符合题意;
B、∵一条对角线平分一组对角的四边形不一定是菱形,
∴选项B符合题意;
C、∵四边相等的四边形是菱形,
∴选项C不符合题意;
D、∵对角线互相垂直平分的四边形是菱形,
∴选项D不符合题意;
故选:B.
3.解:∵四边形为矩形,
∴OB=OD=OA=OC,
在△EBO与△FDO中,
∵,
∴△EBO≌△FDO(ASA),
∴阴影部分的面积=S△AEO+S△EBO=S△AOB,
∵△AOB与△ABC同底且△AOB的高是△ABC高的,
∴S△AOB=S△OBC=S矩形ABCD.
故选:B.
4.解:A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;
B、对角线互相垂直的平行四边形是菱形;故本选项错误;
C、对角线互相平分的四边形是平行四边形;故本选项正确;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误;
故选:C.
5.解:∵∠C=90°,AC=6,BC=8,
∴AB==10,
若以AC,BC为边,则平行四边形的周长=2(AC+BC)=2×(6+8)=28,
若以AC,AB为边,则平行四边形的周长=2(AC+AB)=2×(6+10)=32,
若以AB,BC为边,则平行四边形的周长=2(AB+BC)=2×(10+8)=36,
故选:D.
6.解:∵由题意可知CE是∠BCD的平分线,
∴∠BCE=∠DCE.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DCE=∠E,
∴∠BCE=∠AEC,
∴BE=BC=5,
∵AB=3,
∴AE=BE﹣AB=2,
故选:D.
7.解:如图:过点A作AE⊥x轴于点E,过点B作BF⊥⊥x轴于点F,过点A作AN⊥BF于点N,
过点C作CM⊥x轴于点M,
∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,
∴∠EAO=∠COM,
又∵∠AEO=∠CMO,
∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,
∴∠BAN=∠EAO=∠COM,
在△ABN和△OCM中
,
∴△ABN≌△OCM(AAS),
∴BN=CM,
∵点A(﹣1,2),点B的纵坐标是,
∴BN=,
∴CM=,
∴MO=3,
∴点C的坐标是:(3,).
故选:D.
8.解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A错误;
若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;
若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;
若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.
9.解:∵四边形ABCD是菱形,
∴OB=OD,AC⊥BD,∠ADC=∠ABC,
∵DH⊥AB,
∴OH=OB=BD,
∵∠DHO=20°,
∴∠OHB=90°﹣∠DHO=70°,
∴∠ABD=∠OHB=70°,
∴∠ADC=∠ABC=2∠ABD=140°,
故选:C.
10.解:∵四边形ABCD是平行四边形,
∴BC=AD=6,OA=OC,
∵AC⊥BC,AB=10,
∴==8,
∴AO=CO=AC=4,
∴OB===2;
故选:A.
11.
解:如图 ①AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形;
②∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边;
③∵AB∥CD,∴∠B+∠C=180°,
∵∠A=∠C,∴∠B+∠A=180°,
∴AD∥BC,
∴四边形ABCD是平行四边;
④∵BC∥AD,∴∠B+∠A=180°,
∵∠A=∠C,∴∠B+∠C=180°,
∴AB∥CD,
∴四边形ABCD是平行四边;
故选:B.
12.解:当一个直角三角形的两直角边分别是6,8时,
由勾股定理得,斜边==10,
则斜边上的中线=×10=5,
当8是斜边时,斜边上的中线是4,
故选:D.
13.解:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=∠AOD=90°,
∴四边形AODE是矩形,
故选:C.
14.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,∠EDO=∠FBO,
∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,
∴BO=DO,EF⊥BD,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∵BO=DO,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形,
∴BE=DE,
∵AB=5,AD=12,∠A=90°,
∴BD=13,
设DE=x,则AE=12﹣x,
在Rt△AEB中,AB2+AE2=BE2,
即52+(12﹣x)2=x2,
∴x=,
∴BE=DE=,
在Rt△BEO中,OE=,
∴EF=2EO=,
∴菱形BEDF的面积=,
故选:A.
15.解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=DE,AG=CG,DG=EG,
∴DG=AG=CG=EG,
在Rt△AED中,AD2+AE2=DE2=AC2=(2AG)2=4AG2,故④正确;
∵AE=BD=BC,AG=AC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
16.解:分两种情况讨论:
①当E点在线段DC上时,
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵,AD'=AD,
∴BE=AB=10,
∵,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上时,如下图,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵,
∴DE=D″E=BD''+BE=8+10=18.
综上所知,DE=2或18.
故选:D.
17.解:①∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,
故正确;
②∵EF=,
∴OE=2,
∵AO=AB=3,
∴AE=AO+OE=2+3=5,
故正确;
③作DH⊥AB于H,作FG⊥CO交CO的延长线于G,
则FG=1,
CF=,
BH=3﹣1=2,
DH=3+1=4,
BD=,
故错误;
④△COF的面积S△COF=×3×1=,
故错误;
故选:B.
18.解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADB=∠ADC=60°,
∴△ABD是等边三角形,
∴AD=BD,
又∵△DEF是等边三角形,
∴∠EDF=∠DEF=60°,
又∵∠ADB=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,,
∴△ADE≌△BDF(ASA),
∴AE=BF,
∵AE=t,CF=2t,
∴BF=BC﹣CF=5﹣2t,
∴t=5﹣2t
∴t=,
故选:D.
19.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠DAB=90°,∠ADB=∠CDB=45°.
∵△BEC是等边三角形,
∴BC=BE=CE,∠EBC=∠BCE=∠BEC=60°,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴∠BAE=∠BEA=∠CED=∠CDE=75°,
∴∠EAD=∠EDA=15°,
∴∠DEF=30°,
∴∠CEF=45°.故①正确;
②∵∠EDC=75°,∠BDC=45°,
∴∠EDB=30°,
∴∠DEF=∠EDG.∠EGD=75°.
∵∠ADC=90°,∠DAF=15°,
∴∠EFD=75°,
∴∠EFD=∠EGD.
在△DEF和△EDG中,
,
∴△DEF≌△EDG(AAS),
∴DF=EG.
∵EC=DC,
∴EC﹣EG=DC﹣DF,
∴CG=CF,
∴∠CGF=∠CFG=75°,
∴∠CED=∠CGF,
∴GF∥ED.故②正确;
③由图可知2(OH+HD)=2OD=BD,所以2OH+DH=BD此结论不正确;
④作BM⊥CG于M,DN⊥CG于N,
∴∠BMC=∠DNC=90°,
设AB=BC=CD=AD=x,
∴BM=x,DN=x.
∵,
∴=,
∴BG=DG.故④错误;
故选:C.
20.解:作点E关于BC的对称点E′,连接E′G交BC于点F,此时四边形EFGH周长取最小值,EF=E'F,
过点G作GG′⊥AB于点G′,如图所示.
∵AE=CG,BE=BE′,
∴E′G′=AB=3,
∵GG′=AD=6,
∴E′G===3,
∴C四边形EFGH=2(GF+EF)=2E′G=6.
故选:C.
21.解:过D点作DF⊥x轴,垂足为F,则DF∥y轴,
∵四边形AOCB为矩形,
∴∠OAB=∠AOC=∠B=90°,BC=AO=6,AB=OC,
∵∠BAC=30°,
∴AC=12,OC=AB=,
由折叠可知:∠DAC=∠BAC=30°,AD=AB=,
∴∠OAE=30°,
∴OE=,AE=,
∴ED=,
∵DF∥y轴,
∴∠EDF=∠EAO=30°,
∴EF=,DF=3,
∴OF=OE+EF=,
∴D点坐标为(,﹣3),
故选:B.
22.解:∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC,
∴∠CBD=∠DBA=30°,
∴BD=AD,
∵AD=6,
∴BD=6,
∵P点是BD的中点,
∴CP=BD=3.
故选:A.
23.解:A、由一组邻边相等的平行四边形是菱形可判断?ABCD是菱形;
B、对角线互相垂直的平行四边形是菱形可判断?ABCD是菱形;
C、由AC平分∠BAD,可得四边相等,即可判断?ABCD是菱形;
D、由对角线相等的平行四边形是矩形,可判断?ABCD是矩形.
故选:D.
24.解:连接BP,
(cm2),
∴AB=BC==3(cm),
∴(cm2),
∴,
∴(cm),
故答案为:2.
25.解:∵AF⊥BC,BE⊥AC,D是AB的中点,
∴DE=DF=AB,
∵AB=AC,AF⊥BC,
∴点F是BC的中点,∴BF=FC=3,
∵BE⊥AC,
∴EF=BC=3,
∴△DEF的周长=DE+DF+EF=AB+3=11,
∴AB=8,
故答案为:8.
26.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∵在△ABC和△AED中,
,
∴△ABC≌△EAD.
(2)解:∵AE平分∠DAB(已知),
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°.
∵△ABC≌△EAD,
∴∠AED=∠BAC=85°.
27.证明:(1)∵AF∥BC,
∴∠AFE=∠DBE
∵△ABC是直角三角形,AD是BC边上的中线,E是AD的中点,
∴AE=DE,BD=CD
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS))
∴AF=BD
(2)由(1)知,AF=BD,且BD=CD,
∴AF=CD,且AF∥BC,
∴四边形ADCF是平行四边形
∵∠BAC=90°,D是BC的中点,
∴
∴四边形ADCF是菱形
28.(1)证明:∵∠ADB=∠EDC,
∴∠ADE=∠BDC,
在△ADE和△BDC中,,
∴△ADE≌△BDC(SAS);
(2)解:∵△ADE≌△BDC,
∴∠AED=∠C,
∵∠AEB=36°,
∴∠AED=∠DEC=∠C=(180°﹣36°)=72°,
∴∠EDC=180°﹣2×72°=36°;
(3)证明:∵OB=OE,
∴∠OBE=∠OEB,
∵∠DAE=∠OBE,
∴∠OEB=∠DAE,
∴AD∥BC,
∴∠ADB=∠OBE,
∴∠ADB=∠DAE,
∴OA=OD,
∴AE=BD,
∵AD=BD,
∴AE=AD,
∵△ADE≌△BDC,
∴AE=BC,
∴AD=BC,
∴四边形ABCD是平行四边形.
29.(1)证明:∵CF∥BD,DF∥AC,
∴四边形OCFD是平行四边形,∠OBE=∠CFE,
∴OD=CF,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OB=CF,在
△FCE和△BOE中,,
∴△FCE≌△BOE(AAS);
(2)解:当△ADC满足∠ADC=90°时,四边形OCFD为菱形;理由如下:
∵∠ADC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OC=OD,
∴四边形OCFD为菱形.
30.(1)证明:∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)解:①当∠ACB=45°时,四边形ADCF为正方形;
∵AD=AF,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是菱形,
∴∠ACD=∠ACF=45°,
∴∠DCF=90°,
∴四边形ADCF是正方形;
②当∠ACB=30°时,四边形ABDF为菱形;
∵四边形ADCF是菱形,四边形ABDF是平行四边形,
∴CD=CF,
∵∠ACB=∠ACF=30°,
∴∠DCF=60°,
∴△DCF是等边三角形,
∴DF=CD,
∴DF=BD,
∴四边形ABDF为菱形.
故答案为:45,30.
31.解:(1)证明:∵点O是AC的中点,
∴AO=CO,
∵AM∥BN,
∴∠DAC=∠ACB,
在△AOD和△COB中,,
∴△ADO≌△CBO(ASA);
(2)证明:由(1)得△ADO≌△CBO,
∴AD=CB,
又∵AM∥BN,
∴四边形ABCD是平行四边形,
∵AM∥BN,
∴∠ADB=∠CBD,
∵BD平分∠ABN,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AD=AB,
∴平行四边形ABCD是菱形;
(3)解:由(2)得四边形ABCD是菱形,
∴AC⊥BD,AD=CB,
又DE⊥BD,
∴AC∥DE,
∵AM∥BN,
∴四边形ACED是平行四边形,
∴AC=DE=2,AD=EC,
∴EC=CB,
∵四边形ABCD是菱形,
∴EC=CB=AB=2,
∴EB=4,
在Rt△DEB中,由勾股定理得BD==,
∴.
32.(1)证明:∵AB∥CE,
∴∠CAD=∠ACE,∠ADE=∠CED.
∵F是AC中点,
∴AF=CF.
在△AFD与△CFE中,
.
∴△AFD≌△CFE(AAS),
∴AD=CE,
∴四边形ADCE是平行四边形;
(2)解:过点C作CG⊥AB于点G.
∵CD=BD,∠B=30°,
∴∠DCB=∠B=30°,
∴∠CDA=60°.
在△ACG中,∠AGC=90°,,∠CAG=45°,
∴.
在△CGD中,∠DGC=90°,∠CDG=60°,,
∴GD=1,
∴.
33.(1)证明:①∵CE平分∠ACB,
∴∠OCE=∠BCE,
∵BO⊥CE,
∴∠CFO=∠CFB=90°,
在△OCF与△BCF中,
,
∴△OCF≌△BCF(ASA),
∴OC=BC;
②∵点O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
在△OAD与△OCB中,
,
∴△OAD≌△OCB(ASA),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵OE⊥AC,
∴∠EOC=90°,
在△OCE与△BCE中,
,
∴△OCE≌△BCE(SAS),
∴∠EBC=∠EOC=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AD=BC=3,∠DAB=90°,AC=BD,
∴OB=OC,
∵OC=BC,
∴OC=OB=BC,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠ECB=OCB=30°,
∵∠EBC=90°,
∴EB=EC,
∵BE2+BC2=EC2,BC=3,
∴EB=,EC=2,
∵OE⊥AC,OA=OC,
∴EC=EA=2,
在Rt△ADE中,∠DAB=90°,
∴DE===.
34.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA).
∴AG=AC=8cm,
∴GF=CF,则BG=AB﹣AG=12﹣8=4(cm).
又∵BE=CE,
∴EF是△BCG的中位线.
∴EF=BG=2cm.
答:EF的长为2cm,
35.解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=4,
∴OB=BD=2,
在Rt△AOB中,AB=2,OB=2,
∴OA===4,
∴OE=OA=4.
36.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=AB=×4=8,
∴CE+CG=8是定值.
37.(1)证明:在正方形ABCD中,
∠ABE=∠ADG,AD=AB,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∴∠EAG=90°,
在△FAE和△GAF中,
,
∴△FAE≌△GAF(SAS),
∴EF=FG;
(2)解:如图,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.
∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,
,
∴△ABM≌△ACE(SAS).
∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,
,
∴△MAN≌△EAN(SAS).
∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
∴MN2=BM2+NC2.
∵BM=1,CN=3,
∴MN2=12+32,
∴MN=.
38.(1)证明:∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=FG,
在Rt△ACF与Rt△AGF中,,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG,
∵CD⊥AB,FG⊥AB,
∴CD∥FG,
∴∠CEF=∠EFG,
∴∠CEF=∠CFE,
∴CE=CF,
∴CE=FG,
∵CE∥FG,
∴四边形CEGF是平行四边形,
∵CE=CF,
∴平行四边形CEGF菱形;
(2)解:∵Rt△ACF≌Rt△AGF,
∴AG=AC=6,
∵∠B=30°,∠ACB=90°,
∴AB=2AC=2×6=12,
∴BG=AB﹣AG=12﹣6=6,
∴CE=FG=2.
39.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
∵BC平分∠DBF,
∴∠CBF=∠CBD,
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD,
∴四边形DBFC是菱形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
作CM⊥BF于M,如图:
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=,
∴AC=2.
