北师大版七年级数学下册6.2 频率的稳定性课件(第2课时)(共28张ppt)
文档属性
| 名称 | 北师大版七年级数学下册6.2 频率的稳定性课件(第2课时)(共28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 21:25:48 | ||
图片预览








文档简介
(共28张PPT)
6.2
频率的稳定性
(第2课时)
北师大版
数学
七年级
下册
篮球比赛中,裁判员一般是通过掷硬币决定哪个队先发球,这样的游戏公平吗?为什么?
导入新知
1.
学会根据问题的特点,用统计来估计事件发生的概率,培养分析问题,解决问题的能力.
2.
通过对问题的分析,理解并掌握用频率来估计概率的方法,渗透转化和估算的思想方法.
素养目标
抛掷一枚质地均匀的硬币,硬币落下后,会出现两种情况:
你认为正面朝上和正面朝下的可能性相同吗?
正面朝上
正面朝下
探究新知
知识点
概率
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(1)
同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
动起来!你能行.
探究新知
(2)累计全班同学的试验结果,
并将试验数据汇总填入下表:
试验总次数
20
40
60
80
100
120
140
160
180
200
正面朝上
的次数
正面朝上
的频率
正面朝下
的次数
正面朝下
的频率
探究新知
20
40
60
80
100
120
140
160
180
200
0.2
0.4
0.5
0.6
0.8
1.0
(3)根据上表,完成下面的折线统计图.
频率
试验总次数
探究新知
(4)观察上面的折线统计图,你发现了什么规律?
20
40
60
80
100
120
140
160
180
200
0.2
0.4
0.5
0.6
0.8
1.0
0.2
0.4
0.5
0.6
0.8
1.0
0.2
0.4
0.5
0.6
0.8
1.0
0.2
0.4
0.5
0.6
0.8
1.0
当试验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大.
随着试验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
频率
试验总次数
探究新知
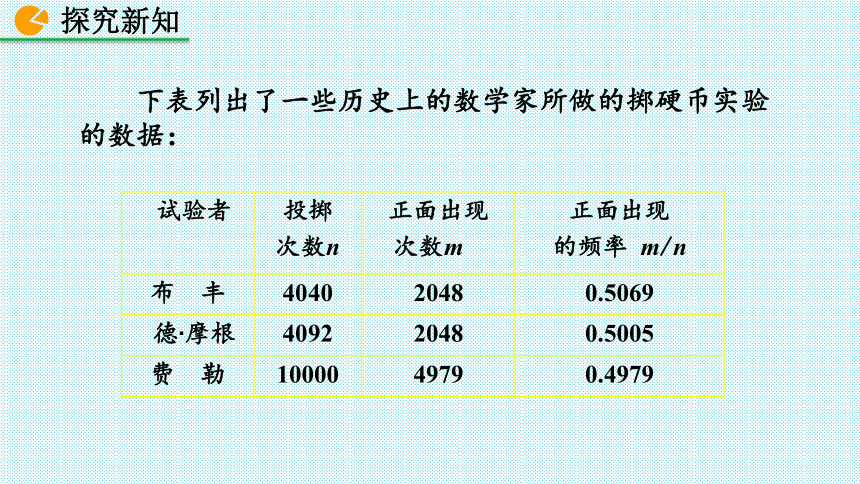
试验者
投掷
次数n
正面出现
次数m
正面出现
的频率
m/n
布
丰
4040
2048
0.5069
德?摩根
4092
2048
0.5005
费
勒
10000
4979
0.4979
下表列出了一些历史上的数学家所做的掷硬币实验的数据:
探究新知
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
维
尼
30000
14994
0.4998
罗曼诺
夫斯基
80640
39699
0.4923
试验者
投掷
次数n
正面出现
次数m
正面出现
的频率
m/n
表中的数据支持你发现的规律吗?
探究新知
无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
由于事件A发生的频率,表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大,因而,我们就用这个常数来表示事件A发生的可能性大小.
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般地,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
探究新知
事件A发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少?
必然事件发生的概率为1;不可能事件发生的概率为0;随机事件A发生的概率P(A)是0与1之间的一个常数.
探究新知
例
王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据(结果保留两位小数):
摸球的次数n
100
150
200
500
800
1000
摸到黑球的次数m
23
31
60
130
203
251
摸到黑球的频率
0.23
0.21
0.30
0.26
0.25
____
探究新知
素养考点
1
用频率估计概率
解:(1)251÷1000≈0.25.因为大量重复试验事件发生的频率逐渐稳定到0.25附近,所以估计从袋中摸出一个球是黑球的概率是0.25;
(2)设袋中白球为x个,1=0.25(1+x),x=3.
答:估计袋中有3个白球.
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是多少?
(2)估算袋中白球的个数.
探究新知
用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指(
)
A.连续掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次硬币,恰好有n次“正面朝上”
D.抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5
D
巩固练习
变式训练
(2020?阜新)掷一枚质地均匀的硬币5次,其中3次正面朝
上,2次正面朝下,则再次掷出这枚硬币,正面朝下的概率
是( )
A.1
B.0.4
C.0.6
D.0.5
D
连接中考
1.下列事件发生的可能性为0的是( )
A.掷两枚骰子,同时出现数字“6”朝上
B.小明从家里到学校用了10分钟,
从学校回到家里却用了15分钟
C.今天是星期天,昨天必定是星期六
D.小明步行的速度是每小时40千米
D
课堂检测
基础巩固题
2.一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是(
)
A.袋子一定有三个白球
B.袋子中白球占小球总数的十分之三
C.再摸三次球,一定有一次是白球
D.再摸1000次,摸出白球的次数会接近330次
D
课堂检测
基础巩固题
3.口袋中有9个球,其中4个红球,3个蓝球,2个白球,在下列事件中,发生的可能性为1
的是(
)
A.从口袋中拿一个球恰为红球
B.从口袋中拿出2个球都是白球
C.拿出6个球中至少有一个球是红球
D.从口袋中拿出的球恰为3红2白
C
课堂检测
基础巩固题
4.2015年4月30日,苏州吴江蚕种全部发放完毕,共计发放蚕种6460张(每张上的蚕卵有200粒左右),涉及6个镇,各镇随即开始孵化蚕种,小李所记录的蚕种孵化情况如表所示,则可以估计蚕种孵化成功的概率为(
)
A.0.95
B.0.9
C.0.85
D.0.8
B
累计蚕种孵化总数/粒
200
400
600
800
1000
1200
1400
孵化成功数/粒
181
362
541
718
905
1077
1263
课堂检测
基础巩固题
5.小明抛掷一枚均匀的硬币,正面朝上的概率为
,那么,抛掷100次硬币,你能保证恰好50次正面朝上吗?
1
2
答:不能,这是因为频数和频率的随机性以及一定的规律性.或者说概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
课堂检测
基础巩固题
对某批乒乓球的质量进行随机抽查,如下表所示:
随机抽取的乒乓球数n
10
20
50
100
200
500
1000
优等品数m
7
16
43
81
164
414
825
优等品率m/n
(1)完成上表;
0.7
0.8
0.86
0.81
0.82
0.828
0.825
课堂检测
能力提升题
(3)如果重新再抽取1000个乒乓球进行质量检查,
对比上表记录下数据,两表的结果会一样吗?
为什么?
(2)根据上表,在这批乒乓球中任取一个,它为
优等品的概率大约是多少?
0.82
答:不一定,这是因为频数和频率的随机性.
课堂检测
下表记录了一名球员在罚球线上投篮的结果,
(1)计算并填写表中的投中频率(精确到0.01);
投篮次数(n)
50
100
150
209
250
300
350
投中次数(m)
28
60
78
104
123
152
175
投中频率(n/m)
0.56
0.60
____
____
0.49
___
____
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
课堂检测
拓广探索题
解:(1)根据题意得:78÷150=0.52;104÷209≈0.50;152÷300≈0.51;175÷350=0.5;
填表如下:
投篮次数(n)
50
100
150
209
250
300
350
投中次数(m)
28
60
78
104
123
152
175
投中频率(n/m)
0.56
0.60
0.52
0.50
0.49
0.51
0.5
课堂检测
(2)由题意得:
投篮的总次数是50+100+150+209+250+300+350=1409(次),
投中的总次数是28+60+78+104+123+152+175=720(次),
则这名球员投篮的次数为1409次,投中的次数为720次,
故这名球员投篮一次,投中的概率约为:
≈0.5.
课堂检测
4.必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件A发生的概率P(A)是0与1之间的一个
常数.
3.一般地,大量重复的试验中,我们常用随机
事件A发生的频率来估计事件A发生的概率.
2.事件A的概率,记为P(A).
1.频率的稳定性.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
6.2
频率的稳定性
(第2课时)
北师大版
数学
七年级
下册
篮球比赛中,裁判员一般是通过掷硬币决定哪个队先发球,这样的游戏公平吗?为什么?
导入新知
1.
学会根据问题的特点,用统计来估计事件发生的概率,培养分析问题,解决问题的能力.
2.
通过对问题的分析,理解并掌握用频率来估计概率的方法,渗透转化和估算的思想方法.
素养目标
抛掷一枚质地均匀的硬币,硬币落下后,会出现两种情况:
你认为正面朝上和正面朝下的可能性相同吗?
正面朝上
正面朝下
探究新知
知识点
概率
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(1)
同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
动起来!你能行.
探究新知
(2)累计全班同学的试验结果,
并将试验数据汇总填入下表:
试验总次数
20
40
60
80
100
120
140
160
180
200
正面朝上
的次数
正面朝上
的频率
正面朝下
的次数
正面朝下
的频率
探究新知
20
40
60
80
100
120
140
160
180
200
0.2
0.4
0.5
0.6
0.8
1.0
(3)根据上表,完成下面的折线统计图.
频率
试验总次数
探究新知
(4)观察上面的折线统计图,你发现了什么规律?
20
40
60
80
100
120
140
160
180
200
0.2
0.4
0.5
0.6
0.8
1.0
0.2
0.4
0.5
0.6
0.8
1.0
0.2
0.4
0.5
0.6
0.8
1.0
0.2
0.4
0.5
0.6
0.8
1.0
当试验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大.
随着试验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
频率
试验总次数
探究新知
试验者
投掷
次数n
正面出现
次数m
正面出现
的频率
m/n
布
丰
4040
2048
0.5069
德?摩根
4092
2048
0.5005
费
勒
10000
4979
0.4979
下表列出了一些历史上的数学家所做的掷硬币实验的数据:
探究新知
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
维
尼
30000
14994
0.4998
罗曼诺
夫斯基
80640
39699
0.4923
试验者
投掷
次数n
正面出现
次数m
正面出现
的频率
m/n
表中的数据支持你发现的规律吗?
探究新知
无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
由于事件A发生的频率,表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大,因而,我们就用这个常数来表示事件A发生的可能性大小.
我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A).
一般地,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
探究新知
事件A发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少?
必然事件发生的概率为1;不可能事件发生的概率为0;随机事件A发生的概率P(A)是0与1之间的一个常数.
探究新知
例
王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据(结果保留两位小数):
摸球的次数n
100
150
200
500
800
1000
摸到黑球的次数m
23
31
60
130
203
251
摸到黑球的频率
0.23
0.21
0.30
0.26
0.25
____
探究新知
素养考点
1
用频率估计概率
解:(1)251÷1000≈0.25.因为大量重复试验事件发生的频率逐渐稳定到0.25附近,所以估计从袋中摸出一个球是黑球的概率是0.25;
(2)设袋中白球为x个,1=0.25(1+x),x=3.
答:估计袋中有3个白球.
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是多少?
(2)估算袋中白球的个数.
探究新知
用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指(
)
A.连续掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次硬币,恰好有n次“正面朝上”
D.抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5
D
巩固练习
变式训练
(2020?阜新)掷一枚质地均匀的硬币5次,其中3次正面朝
上,2次正面朝下,则再次掷出这枚硬币,正面朝下的概率
是( )
A.1
B.0.4
C.0.6
D.0.5
D
连接中考
1.下列事件发生的可能性为0的是( )
A.掷两枚骰子,同时出现数字“6”朝上
B.小明从家里到学校用了10分钟,
从学校回到家里却用了15分钟
C.今天是星期天,昨天必定是星期六
D.小明步行的速度是每小时40千米
D
课堂检测
基础巩固题
2.一个不透明的袋子里有若干个小球,它们除了颜色外,其它都相同,甲同学从袋子里随机摸出一个球,记下颜色后放回袋子里,摇匀后再次随机摸出一个球,记下颜色,…,甲同学反复大量实验后,根据白球出现的频率绘制了如图所示的统计图,则下列说法正确的是(
)
A.袋子一定有三个白球
B.袋子中白球占小球总数的十分之三
C.再摸三次球,一定有一次是白球
D.再摸1000次,摸出白球的次数会接近330次
D
课堂检测
基础巩固题
3.口袋中有9个球,其中4个红球,3个蓝球,2个白球,在下列事件中,发生的可能性为1
的是(
)
A.从口袋中拿一个球恰为红球
B.从口袋中拿出2个球都是白球
C.拿出6个球中至少有一个球是红球
D.从口袋中拿出的球恰为3红2白
C
课堂检测
基础巩固题
4.2015年4月30日,苏州吴江蚕种全部发放完毕,共计发放蚕种6460张(每张上的蚕卵有200粒左右),涉及6个镇,各镇随即开始孵化蚕种,小李所记录的蚕种孵化情况如表所示,则可以估计蚕种孵化成功的概率为(
)
A.0.95
B.0.9
C.0.85
D.0.8
B
累计蚕种孵化总数/粒
200
400
600
800
1000
1200
1400
孵化成功数/粒
181
362
541
718
905
1077
1263
课堂检测
基础巩固题
5.小明抛掷一枚均匀的硬币,正面朝上的概率为
,那么,抛掷100次硬币,你能保证恰好50次正面朝上吗?
1
2
答:不能,这是因为频数和频率的随机性以及一定的规律性.或者说概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
课堂检测
基础巩固题
对某批乒乓球的质量进行随机抽查,如下表所示:
随机抽取的乒乓球数n
10
20
50
100
200
500
1000
优等品数m
7
16
43
81
164
414
825
优等品率m/n
(1)完成上表;
0.7
0.8
0.86
0.81
0.82
0.828
0.825
课堂检测
能力提升题
(3)如果重新再抽取1000个乒乓球进行质量检查,
对比上表记录下数据,两表的结果会一样吗?
为什么?
(2)根据上表,在这批乒乓球中任取一个,它为
优等品的概率大约是多少?
0.82
答:不一定,这是因为频数和频率的随机性.
课堂检测
下表记录了一名球员在罚球线上投篮的结果,
(1)计算并填写表中的投中频率(精确到0.01);
投篮次数(n)
50
100
150
209
250
300
350
投中次数(m)
28
60
78
104
123
152
175
投中频率(n/m)
0.56
0.60
____
____
0.49
___
____
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
课堂检测
拓广探索题
解:(1)根据题意得:78÷150=0.52;104÷209≈0.50;152÷300≈0.51;175÷350=0.5;
填表如下:
投篮次数(n)
50
100
150
209
250
300
350
投中次数(m)
28
60
78
104
123
152
175
投中频率(n/m)
0.56
0.60
0.52
0.50
0.49
0.51
0.5
课堂检测
(2)由题意得:
投篮的总次数是50+100+150+209+250+300+350=1409(次),
投中的总次数是28+60+78+104+123+152+175=720(次),
则这名球员投篮的次数为1409次,投中的次数为720次,
故这名球员投篮一次,投中的概率约为:
≈0.5.
课堂检测
4.必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件A发生的概率P(A)是0与1之间的一个
常数.
3.一般地,大量重复的试验中,我们常用随机
事件A发生的频率来估计事件A发生的概率.
2.事件A的概率,记为P(A).
1.频率的稳定性.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
