1.1.2《程序框图与算法的基本逻辑结构》(新人教版必修3)
文档属性
| 名称 | 1.1.2《程序框图与算法的基本逻辑结构》(新人教版必修3) |

|
|
| 格式 | rar | ||
| 文件大小 | 228.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-30 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第一章 算法初步
1.1.2《程序框图与算法的基本逻辑结构》
1.算法的概念是什么?
在数学中,按照一定规则解决某一类问题的明确和有限的步骤称为算法.
一、复习回顾
2.算法的步骤
我们可以用自然语言表述一个算法,但往往过程复杂,缺乏简洁性
因此,我们有必要探究使算法使算法的结构更清楚、步骤更直观也更精确的方法
这个想法可以实现吗?
3.通过1.1.1节算法可以看出
算法的步骤
有明确的顺序性
有些步骤只有在一定条件下才会被执行
有些步骤在一定条件下会被重复执行
因此,探究使算法的结构更清楚、步
骤更直观也更精确的方法,我们的这个
想法是可以实现的!
一、复习回顾
程序框图
§1.1.2
程序框图
与算法的基本逻辑结构
第一课时
二、讲授新课
1、程序框图
(1)程序框图的概念
程序框图又称流程图,是一种用程序框、流程线及文字说明来准确、直观地表示算法的图形.
程序框图是算法的一种表现形式,也就是说,一个算法可以用算法的步骤表示,也可以用程序框图表示,所以,通常是先写出算法的步骤,然后再转化为对应的程序框图。
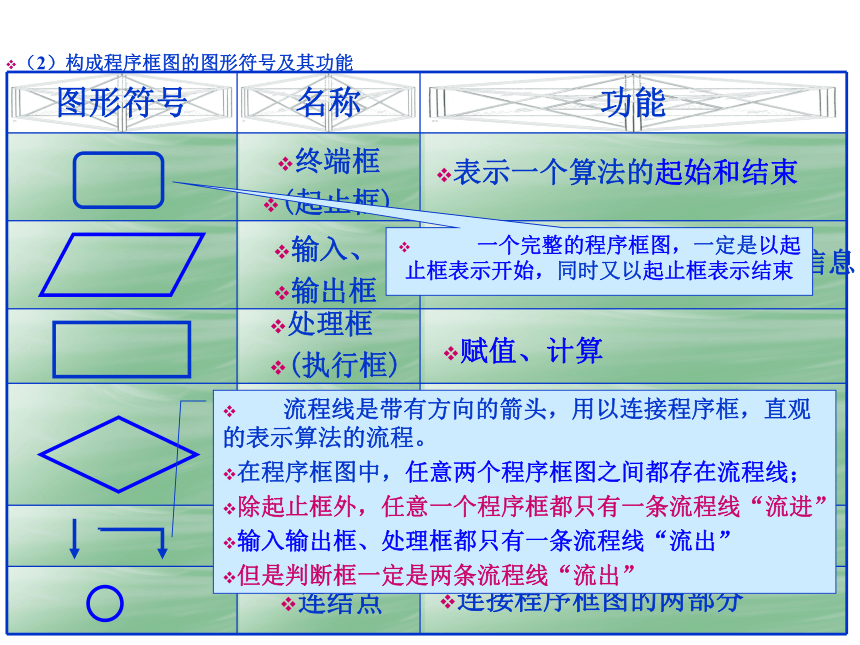
(2)构成程序框图的图形符号及其功能
图形符号 名称 功能
终端框
(起止框)
输入、
输出框
处理框
(执行框)
判断框
表示一个算法的起始和结束
表示一个算法输入和输出的信息
赋值、计算
判断某一条件是否成立
成立时在出口处标明“是”或“Y
不成立时标明“否”或“N”.
流程线
连接程序框
连结点
连接程序框图的两部分
一个完整的程序框图,一定是以起止框表示开始,同时又以起止框表示结束
流程线是带有方向的箭头,用以连接程序框,直观的表示算法的流程。
在程序框图中,任意两个程序框图之间都存在流程线;
除起止框外,任意一个程序框都只有一条流程线“流进”
输入输出框、处理框都只有一条流程线“流出”
但是判断框一定是两条流程线“流出”
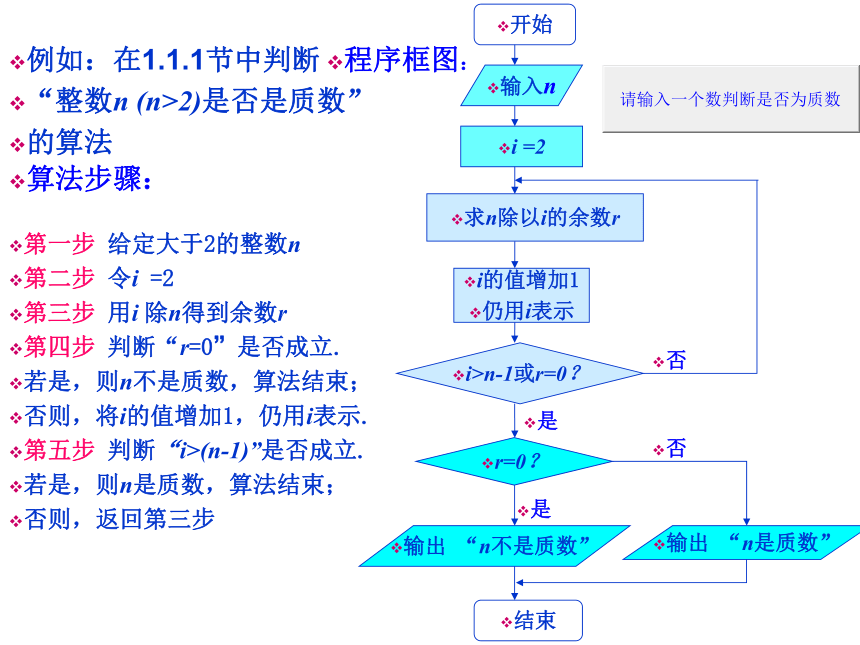
例如:在1.1.1节中判断
“整数n (n>2)是否是质数”
的算法
第一步 给定大于2的整数n
第二步 令i =2
第三步 用i 除n得到余数r
第四步 判断“r=0”是否成立.
若是,则n不是质数,算法结束;
否则,将i的值增加1,仍用i表示.
第五步 判断“i>(n-1)”是否成立.
若是,则n是质数,算法结束;
否则,返回第三步
算法步骤:
程序框图:
开始
输入n
i =2
求n除以i的余数r
i的值增加1
仍用i表示
i>n-1或r=0?
r=0?
结束
输出 “n不是质数”
输出 “n是质数”
是
是
否
否
开始
输入n
i =2
求n除以i的余数r
i的值增加1
仍用i表示
i>n-1或r=0?
r=0?
结束
输出 “n不是质数”
输出 “n是质数”
是
是
否
否
用程序框图表示算法时,算法的逻辑结构展现得非常清楚
顺序结构
循环结构
条件结构
算法的三种基本逻辑结构
你能说出这三种基本逻辑结构的特点吗?
条件结构与循环结构有什么区别和联系?
2、算法的三种基本逻辑结构
顺序结构、条件结构、循环结构。
顺序结构是由若干个依次执行的步骤组成的。这是任何一个算法都离不开的一种基本算法结构。
(1)顺序结构
顺序结构可以用程序框图表示为:
步骤 n
步骤 n+1
例3 已知一个三角形的三边长分别为a, b, c,利用海伦-秦九韶公式设计一个计算三角形面积的算法,并画出程序框图表示.
算法步骤:
第一步,输入三角形三边长a,b,c
第二步,计算
第三步,计算
第四步,输出s.
程序框图:
结 束
开 始
输入a, b, c
输出s
程序框图:
结束
开始
输入 r
输出s
练习1:任意给定一个正实数,设计一个算法求以这个数为半径的圆的面积,并画出程序框图表示.
算法步骤:
第一步,输入圆的半径 r .
第二步,计算S=πr2
第三步,输出S.
计算 S=πr2
在算法中,通过对某个条件的判断,根据条件是否成立选择不同流向的算法结构称为条件结构。
(2)条件结构
条件结构可以用程序框图表示为下面两种形式:
满足条件?
步骤A
步骤B
是
否
满足条件?
步骤A
是
否
例4 任意给定3个正实数,设计一个算法,判断分别以这三个数为三边边长的三角形是否存在.画出这个算法的程序框图.
算法步骤:
第一步,输入3个正实数 a , b, c .
第二步,判断
a+ b>c, a+ c>b,
b+ c>a是否同时成立
若是,则存在这样的三角形;
否则,不存在这样的三角形。
程序框图:
结束
开始
输入 a,b,c
存在这样的三角形
a+ b>c, a+ c>b,
b+ c>a是否同时
成立
不存在这样的三角形
是
否
练习2:如果学生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”.
用程序框图表示这一算法过程.
程序框图:
结束
开始
输入 A
输出“不及格”
A<60
输出“及格”
是
否
1.下面对算法描述正确的一项是( )
A.同一问题的算法不同,结果必然不同
B.同一问题可以有不同的算法
C.算法只能用图形方式来表示
D.算法只能用自然语言来描述
B
四、练习提升
2.已知x=4,y=2,画出计算w=3x+4y的值的程序框图.
1、掌握程序框的画法和功能。
2、了解什么是程序框图,知道学习程序
框图的意义。
3、掌握顺序结构、条件结构的应用,并
能解决与这两种结构有关的程序框图
的画法。
五、课时小结:
六、课外作业
1、认真阅读课本例5
完成作业
画出解不等式ax+b>0(ab≠0)的程序框图.
2、预习循环结构
请各位老师评委 指导!
第一章 算法初步
1.1.2《程序框图与算法的基本逻辑结构》
1.算法的概念是什么?
在数学中,按照一定规则解决某一类问题的明确和有限的步骤称为算法.
一、复习回顾
2.算法的步骤
我们可以用自然语言表述一个算法,但往往过程复杂,缺乏简洁性
因此,我们有必要探究使算法使算法的结构更清楚、步骤更直观也更精确的方法
这个想法可以实现吗?
3.通过1.1.1节算法可以看出
算法的步骤
有明确的顺序性
有些步骤只有在一定条件下才会被执行
有些步骤在一定条件下会被重复执行
因此,探究使算法的结构更清楚、步
骤更直观也更精确的方法,我们的这个
想法是可以实现的!
一、复习回顾
程序框图
§1.1.2
程序框图
与算法的基本逻辑结构
第一课时
二、讲授新课
1、程序框图
(1)程序框图的概念
程序框图又称流程图,是一种用程序框、流程线及文字说明来准确、直观地表示算法的图形.
程序框图是算法的一种表现形式,也就是说,一个算法可以用算法的步骤表示,也可以用程序框图表示,所以,通常是先写出算法的步骤,然后再转化为对应的程序框图。
(2)构成程序框图的图形符号及其功能
图形符号 名称 功能
终端框
(起止框)
输入、
输出框
处理框
(执行框)
判断框
表示一个算法的起始和结束
表示一个算法输入和输出的信息
赋值、计算
判断某一条件是否成立
成立时在出口处标明“是”或“Y
不成立时标明“否”或“N”.
流程线
连接程序框
连结点
连接程序框图的两部分
一个完整的程序框图,一定是以起止框表示开始,同时又以起止框表示结束
流程线是带有方向的箭头,用以连接程序框,直观的表示算法的流程。
在程序框图中,任意两个程序框图之间都存在流程线;
除起止框外,任意一个程序框都只有一条流程线“流进”
输入输出框、处理框都只有一条流程线“流出”
但是判断框一定是两条流程线“流出”
例如:在1.1.1节中判断
“整数n (n>2)是否是质数”
的算法
第一步 给定大于2的整数n
第二步 令i =2
第三步 用i 除n得到余数r
第四步 判断“r=0”是否成立.
若是,则n不是质数,算法结束;
否则,将i的值增加1,仍用i表示.
第五步 判断“i>(n-1)”是否成立.
若是,则n是质数,算法结束;
否则,返回第三步
算法步骤:
程序框图:
开始
输入n
i =2
求n除以i的余数r
i的值增加1
仍用i表示
i>n-1或r=0?
r=0?
结束
输出 “n不是质数”
输出 “n是质数”
是
是
否
否
开始
输入n
i =2
求n除以i的余数r
i的值增加1
仍用i表示
i>n-1或r=0?
r=0?
结束
输出 “n不是质数”
输出 “n是质数”
是
是
否
否
用程序框图表示算法时,算法的逻辑结构展现得非常清楚
顺序结构
循环结构
条件结构
算法的三种基本逻辑结构
你能说出这三种基本逻辑结构的特点吗?
条件结构与循环结构有什么区别和联系?
2、算法的三种基本逻辑结构
顺序结构、条件结构、循环结构。
顺序结构是由若干个依次执行的步骤组成的。这是任何一个算法都离不开的一种基本算法结构。
(1)顺序结构
顺序结构可以用程序框图表示为:
步骤 n
步骤 n+1
例3 已知一个三角形的三边长分别为a, b, c,利用海伦-秦九韶公式设计一个计算三角形面积的算法,并画出程序框图表示.
算法步骤:
第一步,输入三角形三边长a,b,c
第二步,计算
第三步,计算
第四步,输出s.
程序框图:
结 束
开 始
输入a, b, c
输出s
程序框图:
结束
开始
输入 r
输出s
练习1:任意给定一个正实数,设计一个算法求以这个数为半径的圆的面积,并画出程序框图表示.
算法步骤:
第一步,输入圆的半径 r .
第二步,计算S=πr2
第三步,输出S.
计算 S=πr2
在算法中,通过对某个条件的判断,根据条件是否成立选择不同流向的算法结构称为条件结构。
(2)条件结构
条件结构可以用程序框图表示为下面两种形式:
满足条件?
步骤A
步骤B
是
否
满足条件?
步骤A
是
否
例4 任意给定3个正实数,设计一个算法,判断分别以这三个数为三边边长的三角形是否存在.画出这个算法的程序框图.
算法步骤:
第一步,输入3个正实数 a , b, c .
第二步,判断
a+ b>c, a+ c>b,
b+ c>a是否同时成立
若是,则存在这样的三角形;
否则,不存在这样的三角形。
程序框图:
结束
开始
输入 a,b,c
存在这样的三角形
a+ b>c, a+ c>b,
b+ c>a是否同时
成立
不存在这样的三角形
是
否
练习2:如果学生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”.
用程序框图表示这一算法过程.
程序框图:
结束
开始
输入 A
输出“不及格”
A<60
输出“及格”
是
否
1.下面对算法描述正确的一项是( )
A.同一问题的算法不同,结果必然不同
B.同一问题可以有不同的算法
C.算法只能用图形方式来表示
D.算法只能用自然语言来描述
B
四、练习提升
2.已知x=4,y=2,画出计算w=3x+4y的值的程序框图.
1、掌握程序框的画法和功能。
2、了解什么是程序框图,知道学习程序
框图的意义。
3、掌握顺序结构、条件结构的应用,并
能解决与这两种结构有关的程序框图
的画法。
五、课时小结:
六、课外作业
1、认真阅读课本例5
完成作业
画出解不等式ax+b>0(ab≠0)的程序框图.
2、预习循环结构
请各位老师评委 指导!
