1.1.3《导数的几何意义》(人教A版选修2-2)
文档属性
| 名称 | 1.1.3《导数的几何意义》(人教A版选修2-2) |
|
|
| 格式 | rar | ||
| 文件大小 | 215.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-12 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
教材分析
方法手段
教学程序
教学评价
教学目标
知识基础:导数的概念和导数的计算方法.
本节内容:探究和理解导数的几何意义,体会导数在研究函数单调性,变化快慢等方面的作用.
重要意义:导数为研究变量和函数提供了重要的方法。本节课帮助学生更好地理解导数的概念,并认识到导数是刻画函数的单调性、变化快慢和极值等性质最有效的工具,是本章的关键内容.
教材分析
教学目标
方法手段
教学程序
教学评价
微积分是人类思维的伟大成果之一,是人类经历了2500多年震撼人心的智力奋斗的结果,它开创了向近代数学过渡的新时期.导数的概念是微积分核心概念之一,它有极其丰富的实际背景和广泛的应用。
地位作用
教学重点:
1.导数的几何意义
2.“数形结合,以直代曲”的思想方法。
教学难点:
1. 发现和理解导数的几何意义;
2. 运用导数的几何意义解释函数变化的情况和解决实际问题。
教材分析
教学目标
方法手段
教学程序
教学评价
重点难点
关键:师生一同探究和理解导数的几何意义
知识与技能 :
通过实验探求和理解导数的几何意义;
体会导数在刻画函数性质中的作用;
情感态度与价值观:
渗透逼近和以直代曲思想,激发学生学习兴趣,培养学生不断发现、探索新知识的精神,引导学生从有限中认识无限,体会量变和质变的辩证关系,感受数学思想方法的魅力。
过程与方法:
培养学生分析、抽象、概括等思维能力;
通过“以直代曲”思想的具体运用,使学生达到思维方式的迁移,了解科学的思维方法。
教材分析
教学目标
方法手段
教学程序
教学评价
教学方法:互动式讨论 探索式研究
反馈式评价 启发式小结
教学手段:
借助多媒体(幻灯片等)辅助教学
教材分析
教学目标
方法手段
教学程序
教学评价
学习方法: 自主 合作 探究
以问题为载体,学生活动为主线
知识运用
小结作业
创设情境
探索求知
教学程序
以技术为平台,实验探索获得新知
知识运用
小结作业
教学程序
探索求知
创设情境
创设情景,学生活动
第一环节
知识运用
小结作业
创设情境
教学程序
探索求知
问题1 平面几何中我们是怎样判断直线是否
是圆的割线或切线的呢?
知识运用
小结作业
创设情境
探索求知
教学程序
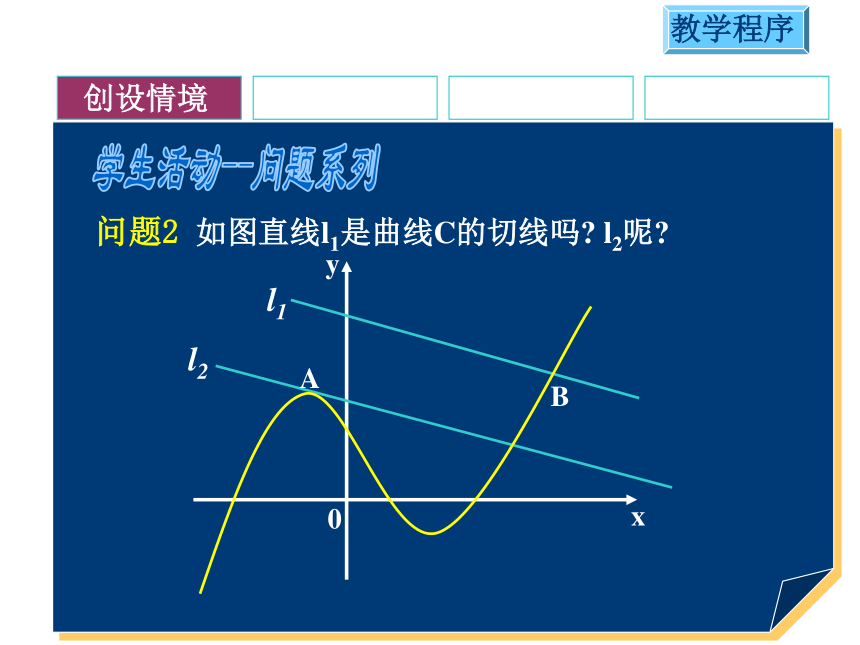
问题2 如图直线l1是曲线C的切线吗 l2呢
l2
l1
A
B
0
x
y
知识运用
小结作业
教学程序
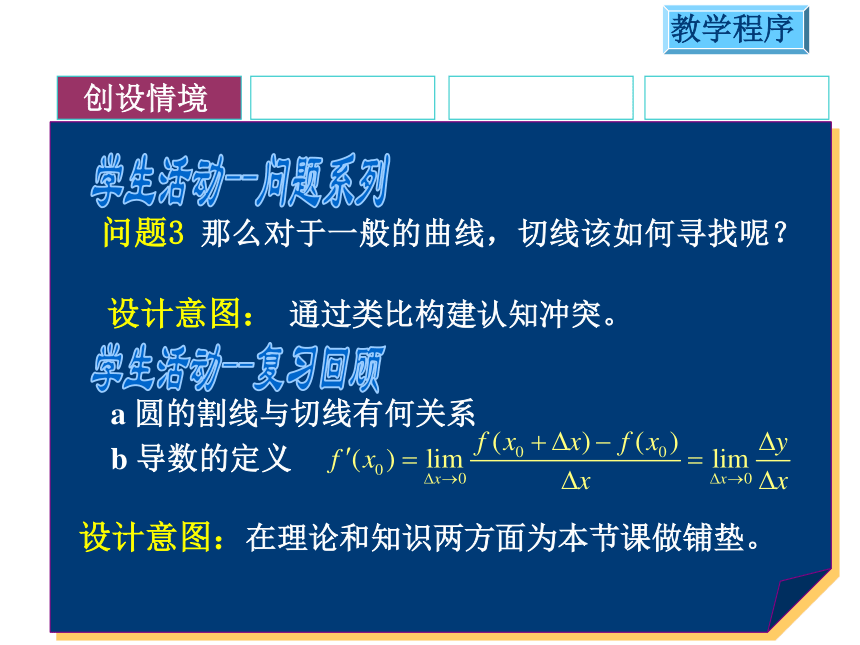
问题3 那么对于一般的曲线,切线该如何寻找呢?
a 圆的割线与切线有何关系
b 导数的定义
探索求知
创设情境
设计意图: 通过类比构建认知冲突。
设计意图:在理论和知识两方面为本节课做铺垫。
知识运用
小结作业
教学程序
探索求知
创设情境
师生互动,探索求知
第二环节
知识运用
小结作业
创设情境
探索求知
教学程序
设计意图:这是从“数”的角度描述导数,为探求导数的几何意义做准备。
问题一: 求导数 的步骤是什么?
第一步:求平均变化 率 ;
第二步:当 趋近于0时,平均变化率
无限趋近于的常数就是 。
知识运用
小结作业
创设情境
探索求知
教学程序
设计意图:通过学生动手实践得到平均变化率
表示割线PQ的斜率。
问题二: 你能借助图像说说平均变化率
表示什么吗?
请在图像中画出来。
知识运用
小结作业
创设情境
探索求知
教学程序
问题三 在 的过程中,你能描述一下割线PQ的变化情况吗?请在图中画出来。
设计意图:分别从“数”和“形”的角度描述 的过程情况。从数的角度看, ,
;从形的角度看, 的过程中,Q点向P点无限趋近,割线PQ趋近于确定的位置,这个位置的直线叫做曲线在 处的切线。
知识运用
小结作业
创设情境
探索求知
教学程序
探究一:随着Q点的移动,观察割线的变化趋势,教师引导给出一般曲线的切线定义。
设计意图:借助多媒体教学手段引导学生发现导数的几何意义,使问题变得直观,易于突破难点;学生在过程中,可以体会逼近的思想方法。能够同时从数与形两个角度强化学生对导数概念的理解。
实幻灯片 15验一
P
Q
o
x
y
y=f(x)
割线
切线
T
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果趋近于确定位置PT.则我们把直线PT称为曲线在点P处的切线.
知识运用
小结作业
创设情境
探索求知
教学程序
问题四:你能从上述过程中概括出函数 在 处的导数 的几何意义吗?
设计意图:引导学生发现并说出: ,割线 PQ
切线PT,所以割线PQ的斜率 切线PT 的斜率。
因此, =切线PT的斜率。
知识运用
小结作业
创设情境
探索求知
教学程序
结论:圆是一种特殊的曲线,圆的切线的定义并不能适用于一般曲线的切线,如图中的 虽然与曲线C有唯一的公共点,但我们不能认为它与曲线C相切。而另一条直线 ,虽然与曲线C有且不只一个公共点,我们还是认为它是曲线C在点A的切线。通过逼近的方法,将割线趋于的确定位置的直线定义为切线,适用于各种曲线。所以这种定义才真正反映了切线的直观本质。
l2
l1
探究二:解决“问题2”
l2
l1
B
0
x
A
小结作业
创设情境
教学程序
探索求知
知识运用
问题五:研究导数的几何意义有什么作用?
结论:以直代曲是微积分中的重要的思想方法,即以简单的对象(切线)来刻画复杂的对象(曲线)。大多数的曲线就一小范围来看,大致可看成直线,所以,某点附近的曲线可以用过此点的切线近似代替,即以直代曲。
P
P
P
① 几何法
小结作业
创设情境
教学程序
探索求知
知识运用
设计意图:与函数概念相类比,很自然地提出导函数概念,为以后的学习做准备.
探究三:导函数的定义
在研究曲线上某点的导数和经过该点的切线斜率的关系这个过程中,可以看到当 时, 是一个确定的数,当 变化时, 是 的一个函数,我们称它为 的导函数,简称导数,也记作 。
知识运用
小结作业
创设情境
探索求知
教学程序
第三环节
知识运用,例题讲解
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
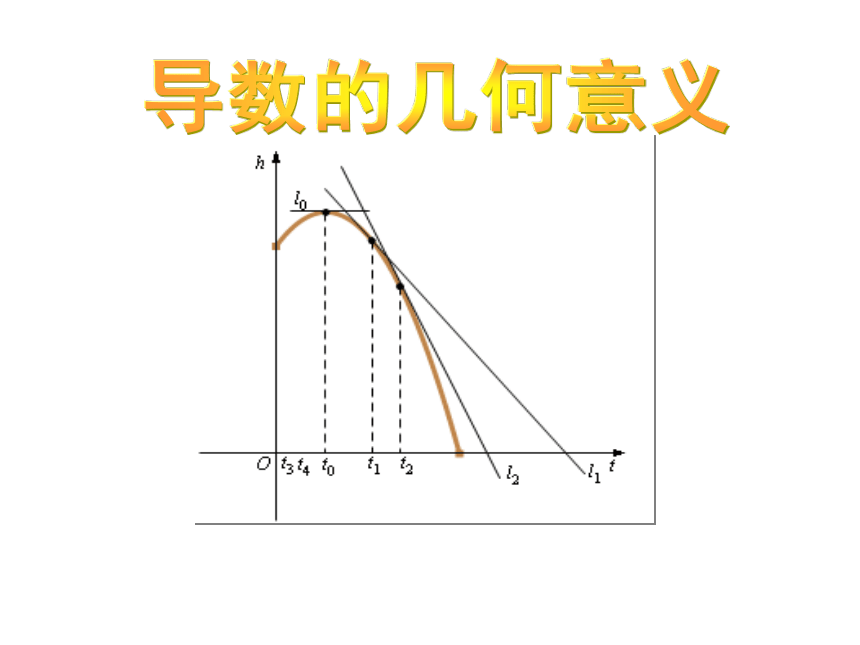
例1 观察跳水运动高度随时间变化的函数
的图象,请描
述曲线在t0,t1,t2附近的变化情况。以
及t1,t2附近的增(减)快慢情况。
探究
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
通过观察跳水问题中导数的变化情况,你得到了哪些结论
(1)以直代曲:大多数函数就一小段范围看,大致可以看作直线,某点附近的曲线可以用过该点的切线近似代替;
(2)函数的单调性与其导函数正负的关系 ;
(3)曲线的变化快慢及切线的倾斜角的内在联系 .
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
归纳小结
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
例2 根据已知条件,画出函数图象在该点附近的大致形状(P11B组T3)
设计意图:体会“以直代曲”的思想方法,以及某点附近的曲线可以用过改点的切线近似代替。
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
练习 已知导函数 的下列信息:
例题处理后,设计的这一组练习是突破难点的关键,也是作为对知识应用的实时检测,给学生提供进一步比较、类比、归纳的机会,为熟练使用新知解决问题打下基础。
练习编排按照由易到难,由简单到复杂的认识规律和心理特征,有利于提高学生的学习积极性。
设计意图
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
知识运用
小结作业
创设情境
探索求知
教学程序
第四环节
当堂小结,布置作业
(1)你学到了哪些知识?
(2)你了解了哪些方法?
知识运用
小结作业
创设情境
探索求知
教学程序
设计意图
1、知识性内容的总结,可以把课堂教学传授的知识尽快地转化为学生的素质;
2、运用数学方法,创新素质的小结能让学生更系统,更深刻地理解数学思想方法在解题中的地位和作用,并且逐渐培养学生的良好个性品质。
知识运用
小结作业
创设情境
探索求知
教学程序
知识运用
小结作业
创设情境
探索求知
教学程序
思考 运用:
1. P10A组第6题。
2.已知函数 ,试画出其导函数图
象的大致形状
探究 拓展:经过曲线上一点P(x0 ,f(x0))的切线方程如何求呢?
设计意图:为下一课时学习求曲线上某点的切线打下基础
知识运用
小结作业
创设情境
探索求知
教学程序
阅读 理解:
收集有关微积分创立的时代背景和牛顿、莱布尼兹的资料
教材分析
教学目标
方法手段
教学程序
教学评价
通过学生参加活动是否积极主动,能否与他人合作
探索,对学生的学习过程评价;
通过学生对方法的选择,对学生的学习能力评价;
通过练习、课后作业,对学生的学习效果评价.
教材分析
教学目标
方法手段
教学程序
教学评价
教学中,学生以研究者的身份学习,在问题解决的
过程中,通过自身的体验对知识的认识从模糊到清
晰,从直观感悟到精确掌握;
本节课设计目标力求使学生体会微积分的基本思想,
感受近似与精确的统一,运动和静止的统一,感受
量变到质变的转化。希望利用这节课渗透辨证法的
思想精髓.
应用领域
应用领域
课题 例1 练习
概念
例2 小结
理解
教材分析
方法手段
教学程序
教学评价
教学目标
知识基础:导数的概念和导数的计算方法.
本节内容:探究和理解导数的几何意义,体会导数在研究函数单调性,变化快慢等方面的作用.
重要意义:导数为研究变量和函数提供了重要的方法。本节课帮助学生更好地理解导数的概念,并认识到导数是刻画函数的单调性、变化快慢和极值等性质最有效的工具,是本章的关键内容.
教材分析
教学目标
方法手段
教学程序
教学评价
微积分是人类思维的伟大成果之一,是人类经历了2500多年震撼人心的智力奋斗的结果,它开创了向近代数学过渡的新时期.导数的概念是微积分核心概念之一,它有极其丰富的实际背景和广泛的应用。
地位作用
教学重点:
1.导数的几何意义
2.“数形结合,以直代曲”的思想方法。
教学难点:
1. 发现和理解导数的几何意义;
2. 运用导数的几何意义解释函数变化的情况和解决实际问题。
教材分析
教学目标
方法手段
教学程序
教学评价
重点难点
关键:师生一同探究和理解导数的几何意义
知识与技能 :
通过实验探求和理解导数的几何意义;
体会导数在刻画函数性质中的作用;
情感态度与价值观:
渗透逼近和以直代曲思想,激发学生学习兴趣,培养学生不断发现、探索新知识的精神,引导学生从有限中认识无限,体会量变和质变的辩证关系,感受数学思想方法的魅力。
过程与方法:
培养学生分析、抽象、概括等思维能力;
通过“以直代曲”思想的具体运用,使学生达到思维方式的迁移,了解科学的思维方法。
教材分析
教学目标
方法手段
教学程序
教学评价
教学方法:互动式讨论 探索式研究
反馈式评价 启发式小结
教学手段:
借助多媒体(幻灯片等)辅助教学
教材分析
教学目标
方法手段
教学程序
教学评价
学习方法: 自主 合作 探究
以问题为载体,学生活动为主线
知识运用
小结作业
创设情境
探索求知
教学程序
以技术为平台,实验探索获得新知
知识运用
小结作业
教学程序
探索求知
创设情境
创设情景,学生活动
第一环节
知识运用
小结作业
创设情境
教学程序
探索求知
问题1 平面几何中我们是怎样判断直线是否
是圆的割线或切线的呢?
知识运用
小结作业
创设情境
探索求知
教学程序
问题2 如图直线l1是曲线C的切线吗 l2呢
l2
l1
A
B
0
x
y
知识运用
小结作业
教学程序
问题3 那么对于一般的曲线,切线该如何寻找呢?
a 圆的割线与切线有何关系
b 导数的定义
探索求知
创设情境
设计意图: 通过类比构建认知冲突。
设计意图:在理论和知识两方面为本节课做铺垫。
知识运用
小结作业
教学程序
探索求知
创设情境
师生互动,探索求知
第二环节
知识运用
小结作业
创设情境
探索求知
教学程序
设计意图:这是从“数”的角度描述导数,为探求导数的几何意义做准备。
问题一: 求导数 的步骤是什么?
第一步:求平均变化 率 ;
第二步:当 趋近于0时,平均变化率
无限趋近于的常数就是 。
知识运用
小结作业
创设情境
探索求知
教学程序
设计意图:通过学生动手实践得到平均变化率
表示割线PQ的斜率。
问题二: 你能借助图像说说平均变化率
表示什么吗?
请在图像中画出来。
知识运用
小结作业
创设情境
探索求知
教学程序
问题三 在 的过程中,你能描述一下割线PQ的变化情况吗?请在图中画出来。
设计意图:分别从“数”和“形”的角度描述 的过程情况。从数的角度看, ,
;从形的角度看, 的过程中,Q点向P点无限趋近,割线PQ趋近于确定的位置,这个位置的直线叫做曲线在 处的切线。
知识运用
小结作业
创设情境
探索求知
教学程序
探究一:随着Q点的移动,观察割线的变化趋势,教师引导给出一般曲线的切线定义。
设计意图:借助多媒体教学手段引导学生发现导数的几何意义,使问题变得直观,易于突破难点;学生在过程中,可以体会逼近的思想方法。能够同时从数与形两个角度强化学生对导数概念的理解。
实幻灯片 15验一
P
Q
o
x
y
y=f(x)
割线
切线
T
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果趋近于确定位置PT.则我们把直线PT称为曲线在点P处的切线.
知识运用
小结作业
创设情境
探索求知
教学程序
问题四:你能从上述过程中概括出函数 在 处的导数 的几何意义吗?
设计意图:引导学生发现并说出: ,割线 PQ
切线PT,所以割线PQ的斜率 切线PT 的斜率。
因此, =切线PT的斜率。
知识运用
小结作业
创设情境
探索求知
教学程序
结论:圆是一种特殊的曲线,圆的切线的定义并不能适用于一般曲线的切线,如图中的 虽然与曲线C有唯一的公共点,但我们不能认为它与曲线C相切。而另一条直线 ,虽然与曲线C有且不只一个公共点,我们还是认为它是曲线C在点A的切线。通过逼近的方法,将割线趋于的确定位置的直线定义为切线,适用于各种曲线。所以这种定义才真正反映了切线的直观本质。
l2
l1
探究二:解决“问题2”
l2
l1
B
0
x
A
小结作业
创设情境
教学程序
探索求知
知识运用
问题五:研究导数的几何意义有什么作用?
结论:以直代曲是微积分中的重要的思想方法,即以简单的对象(切线)来刻画复杂的对象(曲线)。大多数的曲线就一小范围来看,大致可看成直线,所以,某点附近的曲线可以用过此点的切线近似代替,即以直代曲。
P
P
P
① 几何法
小结作业
创设情境
教学程序
探索求知
知识运用
设计意图:与函数概念相类比,很自然地提出导函数概念,为以后的学习做准备.
探究三:导函数的定义
在研究曲线上某点的导数和经过该点的切线斜率的关系这个过程中,可以看到当 时, 是一个确定的数,当 变化时, 是 的一个函数,我们称它为 的导函数,简称导数,也记作 。
知识运用
小结作业
创设情境
探索求知
教学程序
第三环节
知识运用,例题讲解
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
例1 观察跳水运动高度随时间变化的函数
的图象,请描
述曲线在t0,t1,t2附近的变化情况。以
及t1,t2附近的增(减)快慢情况。
探究
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
通过观察跳水问题中导数的变化情况,你得到了哪些结论
(1)以直代曲:大多数函数就一小段范围看,大致可以看作直线,某点附近的曲线可以用过该点的切线近似代替;
(2)函数的单调性与其导函数正负的关系 ;
(3)曲线的变化快慢及切线的倾斜角的内在联系 .
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
归纳小结
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
例2 根据已知条件,画出函数图象在该点附近的大致形状(P11B组T3)
设计意图:体会“以直代曲”的思想方法,以及某点附近的曲线可以用过改点的切线近似代替。
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
练习 已知导函数 的下列信息:
例题处理后,设计的这一组练习是突破难点的关键,也是作为对知识应用的实时检测,给学生提供进一步比较、类比、归纳的机会,为熟练使用新知解决问题打下基础。
练习编排按照由易到难,由简单到复杂的认识规律和心理特征,有利于提高学生的学习积极性。
设计意图
知识运用
小结作业
创设情境
探索求知
教学程序
例
题
讲
解
理
解
掌
握
巩
固
提
高
知识运用
小结作业
创设情境
探索求知
教学程序
第四环节
当堂小结,布置作业
(1)你学到了哪些知识?
(2)你了解了哪些方法?
知识运用
小结作业
创设情境
探索求知
教学程序
设计意图
1、知识性内容的总结,可以把课堂教学传授的知识尽快地转化为学生的素质;
2、运用数学方法,创新素质的小结能让学生更系统,更深刻地理解数学思想方法在解题中的地位和作用,并且逐渐培养学生的良好个性品质。
知识运用
小结作业
创设情境
探索求知
教学程序
知识运用
小结作业
创设情境
探索求知
教学程序
思考 运用:
1. P10A组第6题。
2.已知函数 ,试画出其导函数图
象的大致形状
探究 拓展:经过曲线上一点P(x0 ,f(x0))的切线方程如何求呢?
设计意图:为下一课时学习求曲线上某点的切线打下基础
知识运用
小结作业
创设情境
探索求知
教学程序
阅读 理解:
收集有关微积分创立的时代背景和牛顿、莱布尼兹的资料
教材分析
教学目标
方法手段
教学程序
教学评价
通过学生参加活动是否积极主动,能否与他人合作
探索,对学生的学习过程评价;
通过学生对方法的选择,对学生的学习能力评价;
通过练习、课后作业,对学生的学习效果评价.
教材分析
教学目标
方法手段
教学程序
教学评价
教学中,学生以研究者的身份学习,在问题解决的
过程中,通过自身的体验对知识的认识从模糊到清
晰,从直观感悟到精确掌握;
本节课设计目标力求使学生体会微积分的基本思想,
感受近似与精确的统一,运动和静止的统一,感受
量变到质变的转化。希望利用这节课渗透辨证法的
思想精髓.
应用领域
应用领域
课题 例1 练习
概念
例2 小结
理解
