2.1.2《指数函数的图象与性质》 (新人教A版必修1)
文档属性
| 名称 | 2.1.2《指数函数的图象与性质》 (新人教A版必修1) | 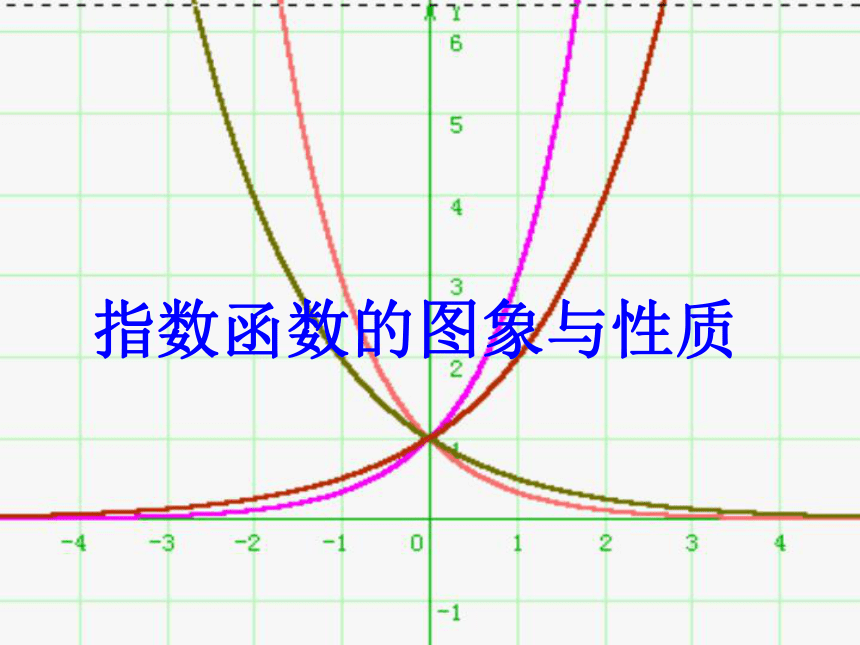 | |
| 格式 | rar | ||
| 文件大小 | 328.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-12 16:40:00 | ||
图片预览








文档简介
(共25张PPT)
指数函数的图象与性质
概念
图象
性质
应用
练习
总结
作业
思考
新课
概念
1.某种细胞分裂时,由1个分裂成两 个,两个分裂成4个……,一个这样的细胞分裂x次后,得到的细胞个数y与x的函数关系是 。
2.某种商品的价格从今年起每年降低15%设原来的价格为1,x年后的价格为y,则y与x的函数关系式?
退出
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
4=22
第x次
……
细胞个数y关于分裂次数x的表达式为
表达式:
2x
8=23
第一题:
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
由上面的对应关系可知,函数关系是:
列表
y
6
5
4
3
2
1
x
0.85
第二题:
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
设问1:象y= , 这类函数与我们以前学习过的 ,一样吗?有没有区别?
设问2:当x取全体实数时,为使y= 有意义,对y= 中的底数a有什么要求?
概念
图象
性质
应用
练习
总结
作业
退出
在
中指数x是自变量,
底数是一个大于0且不等于1的常量.
我们把这种自变量在指数位置上而底数是一个
大于0且不等于1的常量的函数叫做指数函数.
指数函数的定义:
函数
叫做指数函数,其中x是自变量,函数定义域是R。
思考
新课
概念
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
探究1:为什么要规定a>0,且a
1呢?
0时,
①若a=0,则当x>0时,
=0;
无意义.
当x
②若a<0,则对于x的某些数值,可使
无意义.
如
,这时对于x=
,x=
……等等,在实数范围内函数值不存在.
③若a=1,则对于任何x
R,
=1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且a 1。
0
1
a
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
练习:
若
是一个指数函数,求a的取值范围。
解:由指数函数的定义可知,底数应该是大于0
且不等于1的常量。所以,
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
探究2:函数
是指数函数吗?
指数函数的解析式y=
中,
的系数是1.
有些函数看起来不像指数函数,实际上却是,如
因为它可以化为
有些函数貌似指数函数,实际上却不是,如
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
下列函数是否是指数函数:
练习2:
答案:(1) ,(2), (4)是指数函数。
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
1
x
y
o
1
2
3
-1
-2
-3
函数图象特征
概念
图象
性质
应用
练习
总结
作业
图像
退出
x … -3 -2 -1 0 1 2 3 …
y=2-x … 8 4 2 1 1/2 1/4 1/8 …
y=3-x … 27 9 3 1 1/3 1/9 1/27 …
X
O
Y
Y=1
函数图象特征
概念
图象
性质
应用
练习
总结
作业
图像
退出
概念
图象
性质
应用
练习
总结
作业
退出
图像
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题一:
图象分别在哪几个象限?
问题二:
图象的上升、下降与底数a有联系吗?
问题三:
图象中有哪些特殊的点?
答四个图象都在第____象限。
答:当底数__ 时图象上升;当底数____时图象下降.
答:四个图象都经过点____.
Ⅰ、Ⅱ
概念
图象
性质
应用
练习
总结
作业
退出
图像
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题五:
函数 与 图象有
什么关系 ?
问题四:
指数函数 图像是否具有
对称性?
答:
关于y轴对称。
答:
不关于y轴对称不关于原点中心对称
当底数a
取任意值时,指数
函数图象是什么样?
指数函数的图象和性质
概念
图象
性质
应用
练习
总结
作业
退出
图 象
性 质
a>1
0概念
图象
性质
应用
练习
总结
作业
退出
图 象
性 质
(0,1)
y=ax
(a>1)
x
(0,1)
y=1
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
y
x
y=1
y
0
概念
图象
性质
应用
练习
总结
作业
退出
图 象
性 质
(0,1)
y=ax
(a>1)
x
(0,1)
y=1
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
y
x
y=1
y
0
当 x < 0 时,y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,y < 1。
概念
图象
性质
应用
练习
总结
作业
退出
例1
例2
例3
例1、求下列函数的定义域:
解:
①
②
①
②
概念
图象
性质
应用
练习
总结
作业
退出
例1
例2
例3
例2:
已知指数函数
经过点(3,π),求
f(0)、f(1)、f(-3)的值.
(a>0,且a≠1)的图象
概念
图象
性质
应用
练习
总结
作业
退出
例1
例2
例3
概念
图象
性质
概念
练习
总结
作业
退出
练习1
练习2
概念
图象
性质
概念
练习
总结
作业
退出
练习1
练习2
2.练习:
(1,+ )
(0, + )
[1, + )
(0,1]
(-1/2,0)
概念
图象
性质
应用
练习
总结
作业
退出
函数
叫做指数函数,其中x是自变量,函数定义域是R。
1.指数函数的定义:
a>1 0图
象
性
质 1.定义域:R
2.值域:(0,+∞)
3.过点(0,1),即x=0时,y=1
4.在 R上是增函数 在R上是减函数
2.指数函数的的图象和性质:
方法:利用函数图像研究函数性质是一种直观而形象的
方法,记忆指数函数性质时可以联想指数函数的图像。
概念
图象
性质
应用
练习
总结
作业
退出
练习
思考题:A先生从今天开始每天给你10万元,而你第一天给A先生1元,第二天给A先生2元,第三天给A先生4元,第四天给A先生8元……
(1)A先生要和你签订15天的合同,你同意签订这个合同吗?
(2)A先生要和你签订30天的合同,你同意签订这个合同吗?
指数函数的图象与性质
概念
图象
性质
应用
练习
总结
作业
思考
新课
概念
1.某种细胞分裂时,由1个分裂成两 个,两个分裂成4个……,一个这样的细胞分裂x次后,得到的细胞个数y与x的函数关系是 。
2.某种商品的价格从今年起每年降低15%设原来的价格为1,x年后的价格为y,则y与x的函数关系式?
退出
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
4=22
第x次
……
细胞个数y关于分裂次数x的表达式为
表达式:
2x
8=23
第一题:
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
由上面的对应关系可知,函数关系是:
列表
y
6
5
4
3
2
1
x
0.85
第二题:
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
设问1:象y= , 这类函数与我们以前学习过的 ,一样吗?有没有区别?
设问2:当x取全体实数时,为使y= 有意义,对y= 中的底数a有什么要求?
概念
图象
性质
应用
练习
总结
作业
退出
在
中指数x是自变量,
底数是一个大于0且不等于1的常量.
我们把这种自变量在指数位置上而底数是一个
大于0且不等于1的常量的函数叫做指数函数.
指数函数的定义:
函数
叫做指数函数,其中x是自变量,函数定义域是R。
思考
新课
概念
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
探究1:为什么要规定a>0,且a
1呢?
0时,
①若a=0,则当x>0时,
=0;
无意义.
当x
②若a<0,则对于x的某些数值,可使
无意义.
如
,这时对于x=
,x=
……等等,在实数范围内函数值不存在.
③若a=1,则对于任何x
R,
=1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且a 1。
0
1
a
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
练习:
若
是一个指数函数,求a的取值范围。
解:由指数函数的定义可知,底数应该是大于0
且不等于1的常量。所以,
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
探究2:函数
是指数函数吗?
指数函数的解析式y=
中,
的系数是1.
有些函数看起来不像指数函数,实际上却是,如
因为它可以化为
有些函数貌似指数函数,实际上却不是,如
概念
图象
性质
应用
练习
总结
作业
退出
思考
新课
概念
下列函数是否是指数函数:
练习2:
答案:(1) ,(2), (4)是指数函数。
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
1
x
y
o
1
2
3
-1
-2
-3
函数图象特征
概念
图象
性质
应用
练习
总结
作业
图像
退出
x … -3 -2 -1 0 1 2 3 …
y=2-x … 8 4 2 1 1/2 1/4 1/8 …
y=3-x … 27 9 3 1 1/3 1/9 1/27 …
X
O
Y
Y=1
函数图象特征
概念
图象
性质
应用
练习
总结
作业
图像
退出
概念
图象
性质
应用
练习
总结
作业
退出
图像
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题一:
图象分别在哪几个象限?
问题二:
图象的上升、下降与底数a有联系吗?
问题三:
图象中有哪些特殊的点?
答四个图象都在第____象限。
答:当底数__ 时图象上升;当底数____时图象下降.
答:四个图象都经过点____.
Ⅰ、Ⅱ
概念
图象
性质
应用
练习
总结
作业
退出
图像
X
O
Y
Y=1
y=3X
y = 2 x
观察右边图象,回答下列问题:
问题五:
函数 与 图象有
什么关系 ?
问题四:
指数函数 图像是否具有
对称性?
答:
关于y轴对称。
答:
不关于y轴对称不关于原点中心对称
当底数a
取任意值时,指数
函数图象是什么样?
指数函数的图象和性质
概念
图象
性质
应用
练习
总结
作业
退出
图 象
性 质
a>1
0
图象
性质
应用
练习
总结
作业
退出
图 象
性 质
(0,1)
y=ax
(a>1)
x
(0,1)
y=1
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
y
x
y=1
y
0
概念
图象
性质
应用
练习
总结
作业
退出
图 象
性 质
(0,1)
y=ax
(a>1)
x
(0,1)
y=1
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
y
x
y=1
y
0
当 x < 0 时,y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,y < 1。
概念
图象
性质
应用
练习
总结
作业
退出
例1
例2
例3
例1、求下列函数的定义域:
解:
①
②
①
②
概念
图象
性质
应用
练习
总结
作业
退出
例1
例2
例3
例2:
已知指数函数
经过点(3,π),求
f(0)、f(1)、f(-3)的值.
(a>0,且a≠1)的图象
概念
图象
性质
应用
练习
总结
作业
退出
例1
例2
例3
概念
图象
性质
概念
练习
总结
作业
退出
练习1
练习2
概念
图象
性质
概念
练习
总结
作业
退出
练习1
练习2
2.练习:
(1,+ )
(0, + )
[1, + )
(0,1]
(-1/2,0)
概念
图象
性质
应用
练习
总结
作业
退出
函数
叫做指数函数,其中x是自变量,函数定义域是R。
1.指数函数的定义:
a>1 0
象
性
质 1.定义域:R
2.值域:(0,+∞)
3.过点(0,1),即x=0时,y=1
4.在 R上是增函数 在R上是减函数
2.指数函数的的图象和性质:
方法:利用函数图像研究函数性质是一种直观而形象的
方法,记忆指数函数性质时可以联想指数函数的图像。
概念
图象
性质
应用
练习
总结
作业
退出
练习
思考题:A先生从今天开始每天给你10万元,而你第一天给A先生1元,第二天给A先生2元,第三天给A先生4元,第四天给A先生8元……
(1)A先生要和你签订15天的合同,你同意签订这个合同吗?
(2)A先生要和你签订30天的合同,你同意签订这个合同吗?
