2.21《椭圆及其标准方程》(新人教A版选修2-1)
文档属性
| 名称 | 2.21《椭圆及其标准方程》(新人教A版选修2-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-12 16:40:00 | ||
图片预览








文档简介
(共22张PPT)
(第一课时)
在生活中,还有另外一种曲线比较常见,例如
运油车上的贮油罐横截面的外轮廓线
引 言
数 学 实 验
通过图片已经知道了椭圆的形状,能否动手画一个椭圆呢?
先回忆圆的画法:平面内,到定点的距离等于定长的点的轨迹就是圆.
如果把这一个定点分裂成两个定点,会画出什么图形呢?
数 学 实 验
1.取一条定长的细绳;
2.把它的两端固定在图纸上的两点F1、F2;
3.用铅笔尖(M)把细绳拉紧,在图纸上慢慢
移动,看看能画出什么图形?
请同学们按照下列操作,动手画一画:
根据刚才的实验请同学们回答下面
几个问题:
1.在画椭圆的过程中,细绳的两端的位置是固定的还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明了什么?
3.在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系?
数 学 观 察
思考: 结合实验,请同学们思考:椭圆是怎样定义的?
数 学 归 纳
椭圆定义:
我们把平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫椭圆.
两个定点F1、F2叫做椭圆的焦点.
两焦点之间的距离叫做焦距.
数 学 推 理
根据椭圆的定义如何求椭圆的方程呢?
先来回忆:求曲线的方程的基本步骤
(1)建系设点;
(2)写出点集;
(3)列出方程;
(4)化简方程;
(5)检验
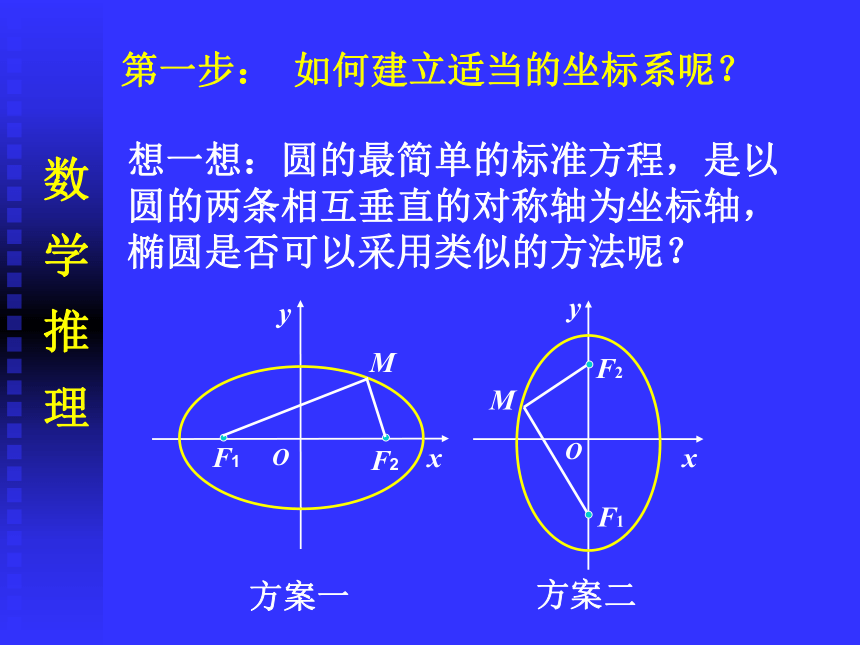
第一步: 如何建立适当的坐标系呢?
数 学 推 理
想一想:圆的最简单的标准方程,是以圆的两条相互垂直的对称轴为坐标轴,椭圆是否可以采用类似的方法呢?
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
数 学 推 理
设M(x, y)是椭圆上任意一点,椭圆的两个焦点分 别为F1和F2,椭圆的焦距为2c(c>0),M与F1和F2 的距离的和等于2a (2a>2c>0)
请同学们自己完成剩下的步骤,求出椭圆的方程.
解:以焦点F1、F2的所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是( c,0)、(c,0) .
x
F1
F2
M
0
y
由椭圆的定义得:
因为
数 学 推 理
方案一
整理得
两边再平方,得
移项,再平方
数 学 推 理
数 学 推 理
它表示焦点在y轴上的椭圆
它表示焦点在x轴上的椭圆
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
数 学 归 纳
椭圆的标准方程有哪些特征呢?
椭圆的标准方程的特征:
(1)椭圆标准方程的形式:左边是两个分式
的平方和,右边是1;
(3)椭圆的标准方程中a、b、c满足a2=b2+c2
(2)椭圆的标准方程中,x2与y2的分母哪一个大,
则焦点在哪一个轴上;
数 学 归 纳
例1 已知椭圆的两个焦点坐标分别是(-2,0),
(2,0), 并且经过点 .求它的标准方程.
解:因为椭圆的焦点在x轴上,所以设
它的标准方程为
由椭圆的定义知
例 题 演 练
例 题 演 练
又因为 ,所以
因此, 所求椭圆的标准方程为
所以
思考?能用其他方法求它的方程么?
解法二:因为椭圆的焦点在x轴上,所以设它
的标准方程为:
①
②
联立①②,
因此, 所求椭圆的标准方程为:
又∵焦点的坐标为
例 题 演 练
1.已知F1、F2是椭圆 的两个焦点,
过F1的直线交椭圆于M、N两点,则三角形
MNF2的周长为 .
课 堂 练 习
20
2.已知椭圆的两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点,求椭圆的方程 .
y
o
F1
F2
M
x
N
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
最后回忆一下本节课的主要内容
课后作业:
1.在椭圆的定义中,若a=c能得到什么图形?若a2.查查资料,看看椭圆还有其他的定义方法么?
3.P42 练习1、4
(第一课时)
在生活中,还有另外一种曲线比较常见,例如
运油车上的贮油罐横截面的外轮廓线
引 言
数 学 实 验
通过图片已经知道了椭圆的形状,能否动手画一个椭圆呢?
先回忆圆的画法:平面内,到定点的距离等于定长的点的轨迹就是圆.
如果把这一个定点分裂成两个定点,会画出什么图形呢?
数 学 实 验
1.取一条定长的细绳;
2.把它的两端固定在图纸上的两点F1、F2;
3.用铅笔尖(M)把细绳拉紧,在图纸上慢慢
移动,看看能画出什么图形?
请同学们按照下列操作,动手画一画:
根据刚才的实验请同学们回答下面
几个问题:
1.在画椭圆的过程中,细绳的两端的位置是固定的还是运动的?
2.在画椭圆的过程中,绳子的长度变了没有?说明了什么?
3.在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系?
数 学 观 察
思考: 结合实验,请同学们思考:椭圆是怎样定义的?
数 学 归 纳
椭圆定义:
我们把平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫椭圆.
两个定点F1、F2叫做椭圆的焦点.
两焦点之间的距离叫做焦距.
数 学 推 理
根据椭圆的定义如何求椭圆的方程呢?
先来回忆:求曲线的方程的基本步骤
(1)建系设点;
(2)写出点集;
(3)列出方程;
(4)化简方程;
(5)检验
第一步: 如何建立适当的坐标系呢?
数 学 推 理
想一想:圆的最简单的标准方程,是以圆的两条相互垂直的对称轴为坐标轴,椭圆是否可以采用类似的方法呢?
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
数 学 推 理
设M(x, y)是椭圆上任意一点,椭圆的两个焦点分 别为F1和F2,椭圆的焦距为2c(c>0),M与F1和F2 的距离的和等于2a (2a>2c>0)
请同学们自己完成剩下的步骤,求出椭圆的方程.
解:以焦点F1、F2的所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是( c,0)、(c,0) .
x
F1
F2
M
0
y
由椭圆的定义得:
因为
数 学 推 理
方案一
整理得
两边再平方,得
移项,再平方
数 学 推 理
数 学 推 理
它表示焦点在y轴上的椭圆
它表示焦点在x轴上的椭圆
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
数 学 归 纳
椭圆的标准方程有哪些特征呢?
椭圆的标准方程的特征:
(1)椭圆标准方程的形式:左边是两个分式
的平方和,右边是1;
(3)椭圆的标准方程中a、b、c满足a2=b2+c2
(2)椭圆的标准方程中,x2与y2的分母哪一个大,
则焦点在哪一个轴上;
数 学 归 纳
例1 已知椭圆的两个焦点坐标分别是(-2,0),
(2,0), 并且经过点 .求它的标准方程.
解:因为椭圆的焦点在x轴上,所以设
它的标准方程为
由椭圆的定义知
例 题 演 练
例 题 演 练
又因为 ,所以
因此, 所求椭圆的标准方程为
所以
思考?能用其他方法求它的方程么?
解法二:因为椭圆的焦点在x轴上,所以设它
的标准方程为:
①
②
联立①②,
因此, 所求椭圆的标准方程为:
又∵焦点的坐标为
例 题 演 练
1.已知F1、F2是椭圆 的两个焦点,
过F1的直线交椭圆于M、N两点,则三角形
MNF2的周长为 .
课 堂 练 习
20
2.已知椭圆的两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点,求椭圆的方程 .
y
o
F1
F2
M
x
N
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
最后回忆一下本节课的主要内容
课后作业:
1.在椭圆的定义中,若a=c能得到什么图形?若a
3.P42 练习1、4
