4.2.1《直线与圆的位置关系》复习课件(新人教A版必修2)
文档属性
| 名称 | 4.2.1《直线与圆的位置关系》复习课件(新人教A版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-12 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
直线与圆的
位置关系应用
d2
△>0
d=r
1
△=0
d>r
0
△<0
数
形
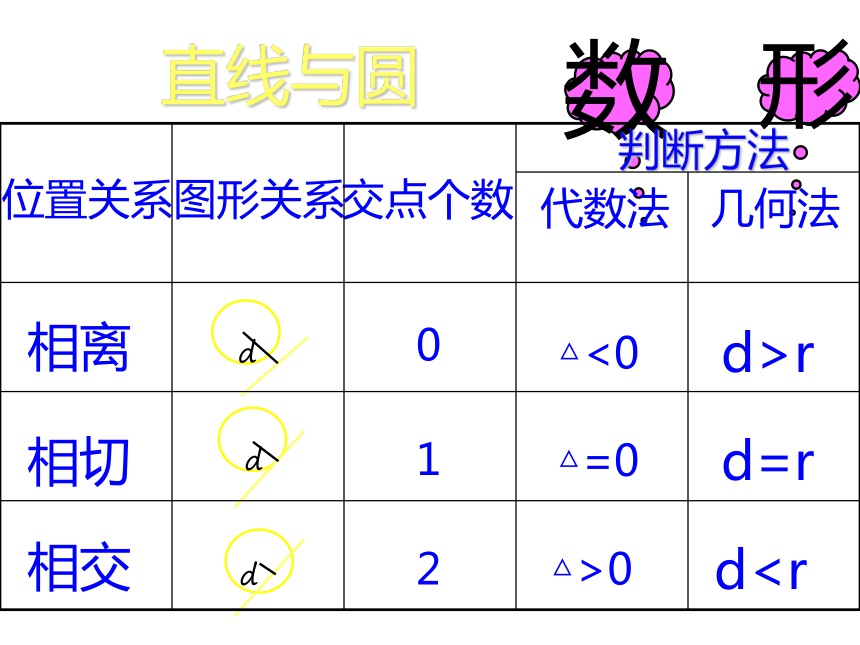
直线与圆
判断方法
位置关系
相交
相切
相离
图形关系
交点个数
代数法
几何法
d
d
d
d
C
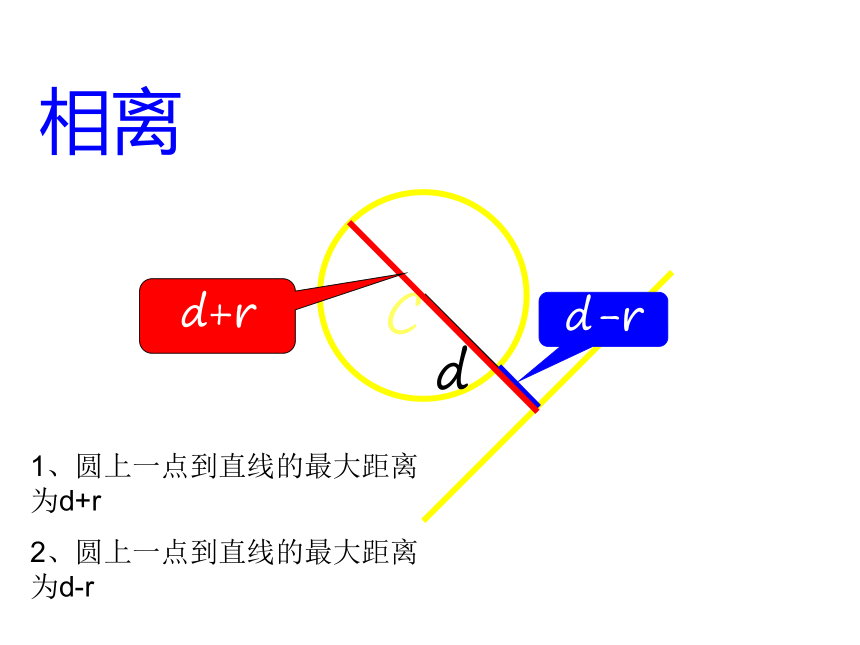
相离
d-r
d+r
1、圆上一点到直线的最大距离为d+r
2、圆上一点到直线的最大距离为d-r
相切
d
C
P
性质:
1.圆心与切点的
连线与切线垂直
2.几何法:d=r
3.代数法:△=0
4.切线长定理:AB=AC
A
C
B
O
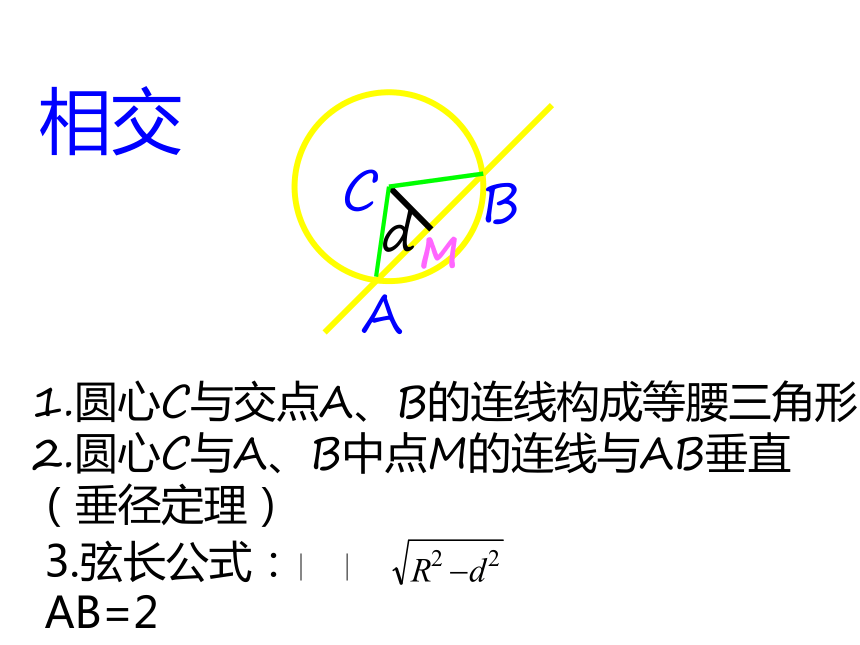
相交
d
C
A
B
M
1.圆心C与交点A、B的连线构成等腰三角形
2.圆心C与A、B中点M的连线与AB垂直
(垂径定理)
3.弦长公式:AB=2
基础练习:
1.直线3x+4y-25=0与圆x2+y2=1的位置
关系是
2.圆心为(1,-3),半径为5的圆在x轴上
截得的弦长为
3.直线与圆x2+y2+2x-4y-3=0相交于A、B
两点,且弦AB中点是(0,1),则
直线AB的方程是
4.由点P(1,1/3)向圆x2+y2+2x-2y-2=0
引的切线方程是
相离
x-y+1=0
4x-3y-3=0或x=1
8
x
y
o
x
y
o
x
y
o
A
B
M
C
x
y
o
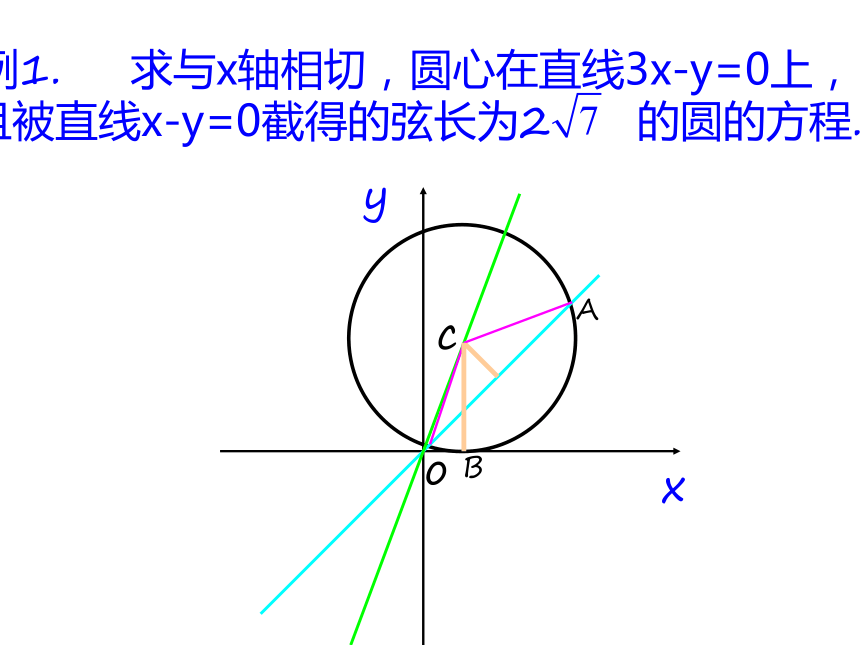
例1. 求与x轴相切,圆心在直线3x-y=0上,
且被直线x-y=0截得的弦长为2 的圆的方程.
x
y
o
c
A
B
例1. 求与x轴相切,圆心在直线3x-y=0上,
且被直线x-y=0截得的弦长为2 的圆的方程.
解:设圆心为(a,b),半径为r
∵圆与x轴相切 ∴r2=b2…………… ①
∵圆心在直线3x-y=0上∴ 3a-b=0…….. ②
∵圆被直线x-y=0截得的弦长为2
且圆心到直线x-y=0的距离为
∴ r2=( )2+( )2 即 2r2=(a-b)2+14….. ③
联立① ② ③,解得a=1,b=3,r=3或a=-1,b=-3,r=3
所求圆方程是(x -1)2+(y -3)2=9或
(x+1)2+(y+3)2=9.
a-b
a-b
变式:求与x轴、y轴都相切,并且截直线 2x+y=0所得弦长为4的圆的方程.
x
y
o
例2.自点A(-3,3)发出的光线L射到x轴上反射后,其反射光线与圆x2+y2-4x-4y+7=0相切,求入射光线L所在的直线方程.
A1
x
y
O
A
C
C1
x
y
O
A
C
4x+3y+3=0 或 3x+4y-2=0
变式:已知点A(-1,1)和圆C:x2+y2-10x-14y+70=0,一束光线从A出发,求经过x轴反射到圆周C的最短路径.
A
x
y
c
A1
总结:
mx2+nx+p=0(m≠ 0)
Ax+By+C=0
(x-a)2+(y-b)2=r2
由方程组:
<0
方程组无解
相离
无交点
=0
方程组有一解
相切
一个交点
>0
相交
方程组有两解
两个交点
代数方法
直线方程L:Ax+By+C=0 圆的方程C:(x-a)2+(y-b)2=r2
=n2-4mp
直线与圆的位置关系的判定
几何方法
直线与圆相离
直线与圆相切
直线与圆相交
d>r
d=r
d演示
小 结
位置
关系
图形
几 何特 征
方程特征 判定方法
几何 法 代数
法
相
交
有两个公共点 方程组有两个不同实根
d△>0
相
切
有且只有一个公共点
方程组有且只有一个实根
d = r
△=0
相
离
没有公共点
方程组无实
根
d>r
△<0
有利于新旧知识的结合,培养学生对知识的迁移能力。 将归纳得出的结论用表格的形式给出,使学生对知识有更完整系统的认识。
直线与圆的
位置关系应用
d
△>0
d=r
1
△=0
d>r
0
△<0
数
形
直线与圆
判断方法
位置关系
相交
相切
相离
图形关系
交点个数
代数法
几何法
d
d
d
d
C
相离
d-r
d+r
1、圆上一点到直线的最大距离为d+r
2、圆上一点到直线的最大距离为d-r
相切
d
C
P
性质:
1.圆心与切点的
连线与切线垂直
2.几何法:d=r
3.代数法:△=0
4.切线长定理:AB=AC
A
C
B
O
相交
d
C
A
B
M
1.圆心C与交点A、B的连线构成等腰三角形
2.圆心C与A、B中点M的连线与AB垂直
(垂径定理)
3.弦长公式:AB=2
基础练习:
1.直线3x+4y-25=0与圆x2+y2=1的位置
关系是
2.圆心为(1,-3),半径为5的圆在x轴上
截得的弦长为
3.直线与圆x2+y2+2x-4y-3=0相交于A、B
两点,且弦AB中点是(0,1),则
直线AB的方程是
4.由点P(1,1/3)向圆x2+y2+2x-2y-2=0
引的切线方程是
相离
x-y+1=0
4x-3y-3=0或x=1
8
x
y
o
x
y
o
x
y
o
A
B
M
C
x
y
o
例1. 求与x轴相切,圆心在直线3x-y=0上,
且被直线x-y=0截得的弦长为2 的圆的方程.
x
y
o
c
A
B
例1. 求与x轴相切,圆心在直线3x-y=0上,
且被直线x-y=0截得的弦长为2 的圆的方程.
解:设圆心为(a,b),半径为r
∵圆与x轴相切 ∴r2=b2…………… ①
∵圆心在直线3x-y=0上∴ 3a-b=0…….. ②
∵圆被直线x-y=0截得的弦长为2
且圆心到直线x-y=0的距离为
∴ r2=( )2+( )2 即 2r2=(a-b)2+14….. ③
联立① ② ③,解得a=1,b=3,r=3或a=-1,b=-3,r=3
所求圆方程是(x -1)2+(y -3)2=9或
(x+1)2+(y+3)2=9.
a-b
a-b
变式:求与x轴、y轴都相切,并且截直线 2x+y=0所得弦长为4的圆的方程.
x
y
o
例2.自点A(-3,3)发出的光线L射到x轴上反射后,其反射光线与圆x2+y2-4x-4y+7=0相切,求入射光线L所在的直线方程.
A1
x
y
O
A
C
C1
x
y
O
A
C
4x+3y+3=0 或 3x+4y-2=0
变式:已知点A(-1,1)和圆C:x2+y2-10x-14y+70=0,一束光线从A出发,求经过x轴反射到圆周C的最短路径.
A
x
y
c
A1
总结:
mx2+nx+p=0(m≠ 0)
Ax+By+C=0
(x-a)2+(y-b)2=r2
由方程组:
<0
方程组无解
相离
无交点
=0
方程组有一解
相切
一个交点
>0
相交
方程组有两解
两个交点
代数方法
直线方程L:Ax+By+C=0 圆的方程C:(x-a)2+(y-b)2=r2
=n2-4mp
直线与圆的位置关系的判定
几何方法
直线与圆相离
直线与圆相切
直线与圆相交
d>r
d=r
d
小 结
位置
关系
图形
几 何特 征
方程特征 判定方法
几何 法 代数
法
相
交
有两个公共点 方程组有两个不同实根
d
相
切
有且只有一个公共点
方程组有且只有一个实根
d = r
△=0
相
离
没有公共点
方程组无实
根
d>r
△<0
有利于新旧知识的结合,培养学生对知识的迁移能力。 将归纳得出的结论用表格的形式给出,使学生对知识有更完整系统的认识。
