8.4《导数与函数的单调性》(北师大版选修2-2)
文档属性
| 名称 | 8.4《导数与函数的单调性》(北师大版选修2-2) |

|
|
| 格式 | rar | ||
| 文件大小 | 606.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-12 00:00:00 | ||
图片预览

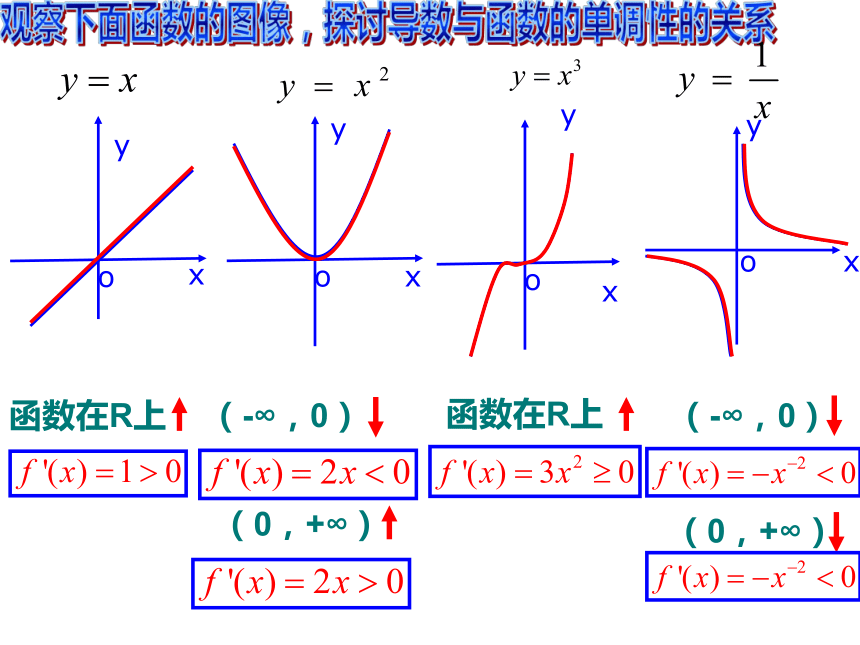



文档简介
(共10张PPT)
y
o
x
x
y
o
x
y
o
函数在R上
(-∞,0)
(0,+∞)
函数在R上
(-∞,0)
(0,+∞)
y
o
x
2
y
x
0
.
.
.
.
.
.
.
再观察函数y=x2-4x+3的图象
函数在区间
(-∞,2)上单调递减,切线斜率小于0,即其导数为负;
总结:
在区间(2,+∞)上单调递增,切线斜率大于0,即其导数为正.
在某个区间(a,b)内,
①如果f’(x)>0,
②如果f’(x)<0,
那么函数y=f(x)在这个区间内单调
递增.
那么函数y=f(x)在这个区间内单调
递减.
如果在某个区间内恒有f’(x)=0,那么函数f(x)
有什么特性?
判断函数
的单调性,
并求出其单调区间.
你能小结求解函数单调区间的步骤吗?
(1)确定函数y=f(x)的定义域;
(2)求导数f’(x);
(3)解不等式f’(x)>0,解集在定义域内的部分
为增区间;
(4)解不等式f’(x)<0,解集在定义域内的部分
为减区间.
因为
所以
当
函数
单调递增.
当
函数
单调递减.
函数 的单调递增区间为
单调递减区间为(-2,1)
应用
设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
x
y
o
1
2
x
y
o
1
2
(A)
(B)
x
y
o
1
2
x
y
o
1
2
(C)
(D)
x
y
o
2
高考链接
课堂练习
求下列函数的单调区间
课本62页 习题3.1 A组 1,2
课后思考:
课本62页 习题3.1 B组
y
o
x
x
y
o
x
y
o
函数在R上
(-∞,0)
(0,+∞)
函数在R上
(-∞,0)
(0,+∞)
y
o
x
2
y
x
0
.
.
.
.
.
.
.
再观察函数y=x2-4x+3的图象
函数在区间
(-∞,2)上单调递减,切线斜率小于0,即其导数为负;
总结:
在区间(2,+∞)上单调递增,切线斜率大于0,即其导数为正.
在某个区间(a,b)内,
①如果f’(x)>0,
②如果f’(x)<0,
那么函数y=f(x)在这个区间内单调
递增.
那么函数y=f(x)在这个区间内单调
递减.
如果在某个区间内恒有f’(x)=0,那么函数f(x)
有什么特性?
判断函数
的单调性,
并求出其单调区间.
你能小结求解函数单调区间的步骤吗?
(1)确定函数y=f(x)的定义域;
(2)求导数f’(x);
(3)解不等式f’(x)>0,解集在定义域内的部分
为增区间;
(4)解不等式f’(x)<0,解集在定义域内的部分
为减区间.
因为
所以
当
函数
单调递增.
当
函数
单调递减.
函数 的单调递增区间为
单调递减区间为(-2,1)
应用
设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
x
y
o
1
2
x
y
o
1
2
(A)
(B)
x
y
o
1
2
x
y
o
1
2
(C)
(D)
x
y
o
2
高考链接
课堂练习
求下列函数的单调区间
课本62页 习题3.1 A组 1,2
课后思考:
课本62页 习题3.1 B组
