5.1.4《不等式的证明》(北师大版选修)
文档属性
| 名称 | 5.1.4《不等式的证明》(北师大版选修) |

|
|
| 格式 | rar | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-12 16:40:23 | ||
图片预览






文档简介
(共17张PPT)
奇峰怪石
古树名花
天
下
第
一
仙
峰
世
上
无
双
福
地
猴王观宝
观音送子
玉京峰
司春女神
海狮望月
巨蟒出山
流泉飞瀑
云海雾涛
天
下
第
一
仙
峰
世
上
无
双
福
地
问题
门票优惠方案,具体如下:
旺季门票原价为200元,现推出两套优惠方案(两人以上集体购票时可选择以下任意一种方案)
优惠方案A:买全票一张,则其余票可享受八折优惠;
优惠方案B:按团体购票,一概优惠30元.
为了使门票花费最少,请各位同学用你们的智慧帮我想一想我该选择哪种方案?说说你的想法.
国庆放假期间,邀上几个同事去了趟三清山,
正好遇见景区推出2套门票优惠方案
合作交流:分成3组,每组讨论一种情况.
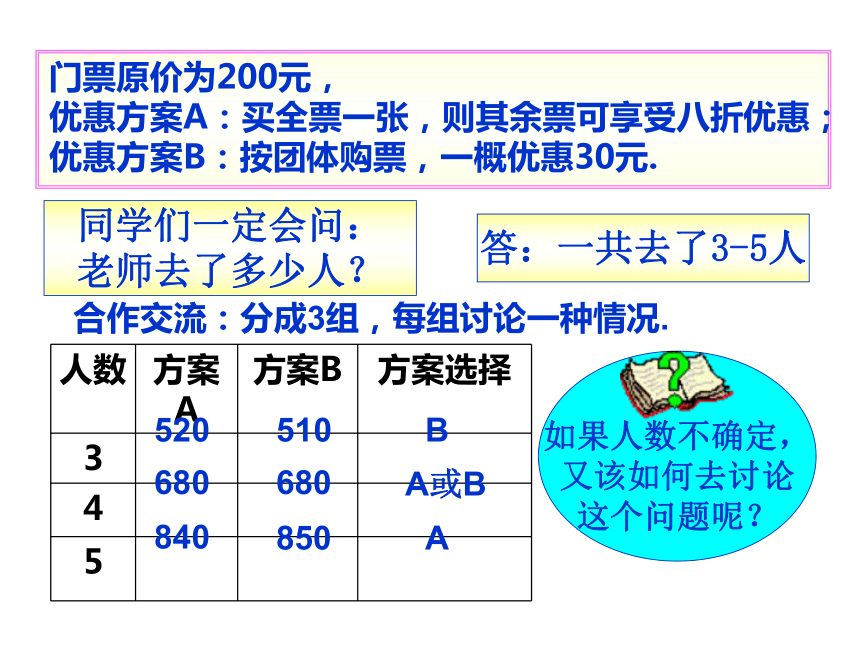
答:一共去了3-5人
人数 方案A 方案B 方案选择
3
4
5
510
520
680
680
A或B
840
850
A
B
如果人数不确定,
又该如何去讨论
这个问题呢?
门票原价为200元,
优惠方案A:买全票一张,则其余票可享受八折优惠;
优惠方案B:按团体购票,一概优惠30元.
同学们一定会问:
老师去了多少人?
方案A:f(n)=200+(n-1)×200×0.8=160n+40
方案B:g(n)=(200-30)n=170n
要知道f(n)与g(n)的大小关系
应作差比较f(n)-g(n)与0的大小.
设人数为n,方案A花费费用为f(n),
方案B花费费用为g(n).则
一.比较法
我们要证明a>b,只要证明a-b>0即可,要证明a<b,只要证明a-b<0即可. 这种方法就称为求差比较法.
例1.
求证:
证明:
证明:
<0
归纳
一般步骤:
作差-变形-判断符号
变形是关键:
1°变形常用手段:
2°变形常见形式是:
配方法,因式分解法
1.变形为常数;
2.几个平方和;
3.一个常数与几个平方和;
4.几个因式的积的形式.
思路分析:作差——变形——定号
配方?
因式分解?
当作差后很难或无法通过变形判断符号时,就要另寻其他解法.
我们知道如果在 a.b均为正数的情况下,
a>b
有
所以要证明a>b,只要证明 即可,要证
明a<b,只要证明 即可.
这种方法就称为求商比较法.
例2:已知a>b>0,求证:aabb>abba
变式:若条件改为a>0且b>0, aabb>abba还成立吗?
求商比较法前提是:两个数都应为正数.
思路分析:作商——变形——与1比较 大小
分析法
从求证的不等式出发,层层推出使这个不等式成立的充分条件,直到得到一个明显成立的不等式或一个比较容易证明的不等式为止,这种证明方法叫做分析法。
证明思路:
思路分析:寻找满足结论的充分条件:
平方——变形——得到证明
方法小结
一.比较法:
①比较法可分为求差比较法(简称作差法)和求商比较法(简称作商法).注意二者的区别.
②一般地,证幂、指数不等式时,常用求商法;证对数不等式,多项式,分式时,常用求差法.
③当“差”或“商”中含有字母而无法判定时,一般需对字母的取值进行分类讨论.
二.分析法:
若证命题B为真,只需证B1为真,从而又只需证B2
为真,从而又……只需证A为真,今已知A为真,
用推出符号简化,即B B1 B2 … Bn A
A组.(必做)课本: 1.2.3.4
已知a,b,c∈R+,
(1)求证:(a+b+c) ≥9
(2)若a+b+c=1,求证: ≥9
B组(选做)
布置作业
奇峰怪石
古树名花
天
下
第
一
仙
峰
世
上
无
双
福
地
猴王观宝
观音送子
玉京峰
司春女神
海狮望月
巨蟒出山
流泉飞瀑
云海雾涛
天
下
第
一
仙
峰
世
上
无
双
福
地
问题
门票优惠方案,具体如下:
旺季门票原价为200元,现推出两套优惠方案(两人以上集体购票时可选择以下任意一种方案)
优惠方案A:买全票一张,则其余票可享受八折优惠;
优惠方案B:按团体购票,一概优惠30元.
为了使门票花费最少,请各位同学用你们的智慧帮我想一想我该选择哪种方案?说说你的想法.
国庆放假期间,邀上几个同事去了趟三清山,
正好遇见景区推出2套门票优惠方案
合作交流:分成3组,每组讨论一种情况.
答:一共去了3-5人
人数 方案A 方案B 方案选择
3
4
5
510
520
680
680
A或B
840
850
A
B
如果人数不确定,
又该如何去讨论
这个问题呢?
门票原价为200元,
优惠方案A:买全票一张,则其余票可享受八折优惠;
优惠方案B:按团体购票,一概优惠30元.
同学们一定会问:
老师去了多少人?
方案A:f(n)=200+(n-1)×200×0.8=160n+40
方案B:g(n)=(200-30)n=170n
要知道f(n)与g(n)的大小关系
应作差比较f(n)-g(n)与0的大小.
设人数为n,方案A花费费用为f(n),
方案B花费费用为g(n).则
一.比较法
我们要证明a>b,只要证明a-b>0即可,要证明a<b,只要证明a-b<0即可. 这种方法就称为求差比较法.
例1.
求证:
证明:
证明:
<0
归纳
一般步骤:
作差-变形-判断符号
变形是关键:
1°变形常用手段:
2°变形常见形式是:
配方法,因式分解法
1.变形为常数;
2.几个平方和;
3.一个常数与几个平方和;
4.几个因式的积的形式.
思路分析:作差——变形——定号
配方?
因式分解?
当作差后很难或无法通过变形判断符号时,就要另寻其他解法.
我们知道如果在 a.b均为正数的情况下,
a>b
有
所以要证明a>b,只要证明 即可,要证
明a<b,只要证明 即可.
这种方法就称为求商比较法.
例2:已知a>b>0,求证:aabb>abba
变式:若条件改为a>0且b>0, aabb>abba还成立吗?
求商比较法前提是:两个数都应为正数.
思路分析:作商——变形——与1比较 大小
分析法
从求证的不等式出发,层层推出使这个不等式成立的充分条件,直到得到一个明显成立的不等式或一个比较容易证明的不等式为止,这种证明方法叫做分析法。
证明思路:
思路分析:寻找满足结论的充分条件:
平方——变形——得到证明
方法小结
一.比较法:
①比较法可分为求差比较法(简称作差法)和求商比较法(简称作商法).注意二者的区别.
②一般地,证幂、指数不等式时,常用求商法;证对数不等式,多项式,分式时,常用求差法.
③当“差”或“商”中含有字母而无法判定时,一般需对字母的取值进行分类讨论.
二.分析法:
若证命题B为真,只需证B1为真,从而又只需证B2
为真,从而又……只需证A为真,今已知A为真,
用推出符号简化,即B B1 B2 … Bn A
A组.(必做)课本: 1.2.3.4
已知a,b,c∈R+,
(1)求证:(a+b+c) ≥9
(2)若a+b+c=1,求证: ≥9
B组(选做)
布置作业
