2020-2021学年苏教版小学六年级数学下册《第6章 正比例和反比例》单元测试题(有答案)
文档属性
| 名称 | 2020-2021学年苏教版小学六年级数学下册《第6章 正比例和反比例》单元测试题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 182.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 19:46:22 | ||
图片预览




文档简介
2020-2021学年苏教版小学六年级数学下册《第6章
正比例和反比例》单元测试题
一.选择题(共8小题)
1.表示x和y成正比例关系的式子是( )
A.x+y=10
B.x﹣y=10
C.y=10x
2.铺地面积一定,( )和用砖块数成反比例.
A.每块砖的边长
B.每块砖的面积
C.每块砖的周长
3.下列两种相关联的量,成正比例的是( )
A.正方形的面积和它的边长
B.路程一定,行驶的速度和时间
C.单价一定,购买商品的数量和总价
D.圆柱的底面积和体积
4.如果x=y,那么x与y成( )比例。
A.正
B.反
C.不成
D.无法确定
5.下列两种量的关系成正比例关系的是( )
A.圆的半径和圆的面积
B.写字总数一定,写一个字所用时间和写字总时间
C.写字总数一定,每分钟写字个数和写字总时间
D.两个互相咬合的齿轮,齿轮的齿数和转数
6.下面图中表示淘气爸爸在高速路上某段路程匀速行驶的是( )
A.
B.
C.
D.
7.全班人数一定,出勤人数和出勤率( )
A.成正比例
B.成反比例
C.不成比例
8.长方形的面积一定,长和宽( )
A.成正比例
B.成反比例
C.不成比例
二.填空题(共8小题)
9.王飞以每小时40千米的速度行了240千米,按原路返回时每小时行60千米,王飞往返的平均速度是每小时行
千米.
10.甲数与乙数的比例为5:3,甲数为60,乙数为
.
11.如果y=5x,那么x和y成
比例.
12.已知xy=5,y与x成
比例。
4.2米80厘米=
厘米
3600mL=
L
6千克50克=
千克
7平方米=
平方分米
13.科技小组制作弹簧秤,弹簧长度与所挂砝码质量存在如下关系(在弹簧弹性承受范围内):
弹簧长度/cm
8
9
10
11
……
kg砝码质量/
0
2
4
6
……
(1)用该弹簧秤称一个物体,弹簧长度是12.8厘米,这个物体质量是
千克。
(2)当所称物体质量为n千克,弹簧长度是
厘米。
14.如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1:3,若阴影三角形面积为1平方厘米,则原长方形面积为
平方厘米.
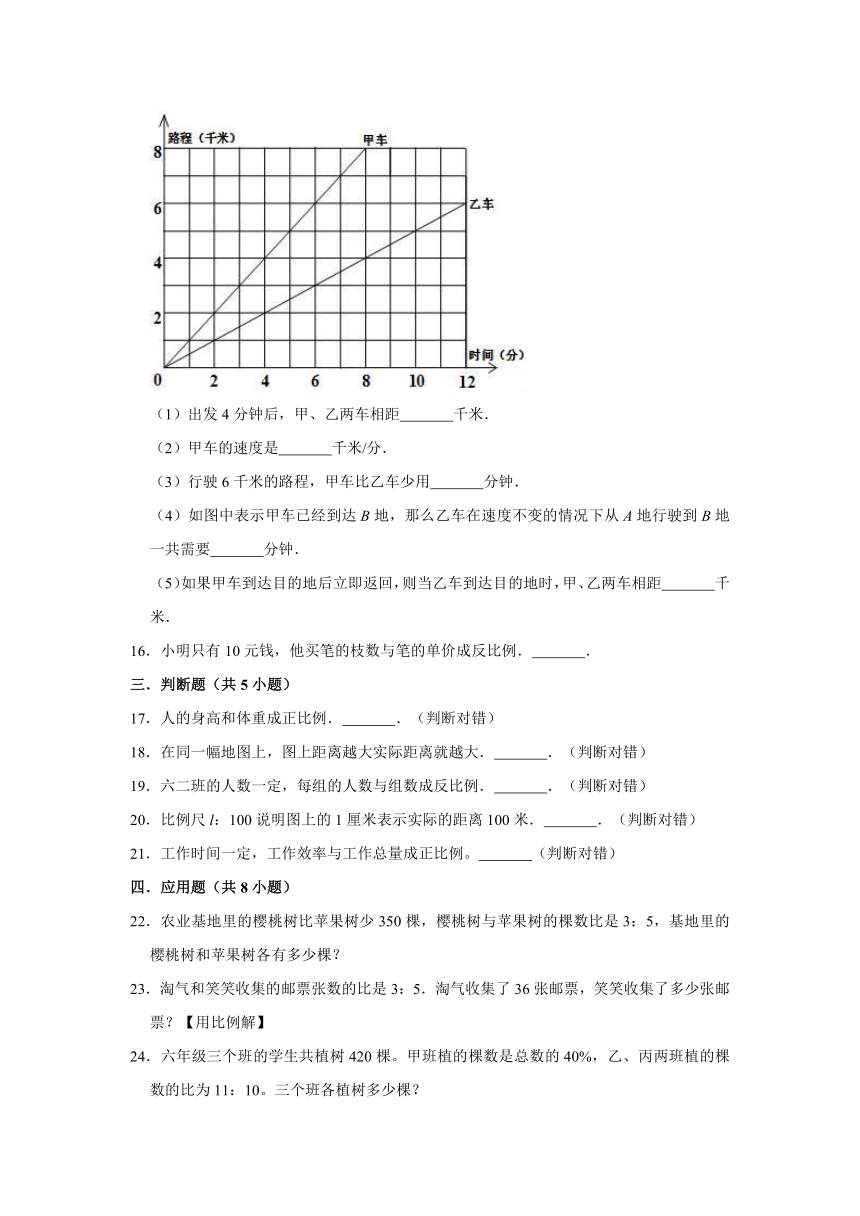
15.如图的统计图表示甲、乙两车同时从A地出发驶向B地的行驶时间和路程情况.请根据图回答以下问题:
(1)出发4分钟后,甲、乙两车相距
千米.
(2)甲车的速度是
千米/分.
(3)行驶6千米的路程,甲车比乙车少用
分钟.
(4)如图中表示甲车已经到达B地,那么乙车在速度不变的情况下从A地行驶到B地一共需要
分钟.
(5)如果甲车到达目的地后立即返回,则当乙车到达目的地时,甲、乙两车相距
千米.
16.小明只有10元钱,他买笔的枝数与笔的单价成反比例.
.
三.判断题(共5小题)
17.人的身高和体重成正比例.
.(判断对错)
18.在同一幅地图上,图上距离越大实际距离就越大.
.(判断对错)
19.六二班的人数一定,每组的人数与组数成反比例.
.(判断对错)
20.比例尺l:100说明图上的1厘米表示实际的距离100米.
.(判断对错)
21.工作时间一定,工作效率与工作总量成正比例。
(判断对错)
四.应用题(共8小题)
22.农业基地里的樱桃树比苹果树少350棵,樱桃树与苹果树的棵数比是3:5,基地里的樱桃树和苹果树各有多少棵?
23.淘气和笑笑收集的邮票张数的比是3:5.淘气收集了36张邮票,笑笑收集了多少张邮票?【用比例解】
24.六年级三个班的学生共植树420棵。甲班植的棵数是总数的40%,乙、丙两班植的棵数的比为11:10。三个班各植树多少棵?
25.如图的图象反映的是购买两种练习本的数量和总价的变化情况.
(1)购买甲种练习本的数量和总价是否成正比例?乙种呢?
(2)估计一下,买5本甲种练习本多少元?2.8元可以买几本甲种练习本?
(3)从图上看哪种练习本便宜些?2.4元可以买两种练习本各多少本?
26.一棵树高12米,它的影长是15米,如果同一时间地点测得小明的身高是1.6米,他的影子长多少米?(用比例解答)
27.铺设一条煤气管道。计划每天铺设120米,用12天完成任务。由于居民着急使用,上级要求每天多铺20%,这样可以提前几天完成?(用比例的知识解)
28.如图的图象表示长颈鹿的奔跑情况.
(1)长颈鹿的奔跑路程与奔跑时间成
比例关系.
(2)请你计算一下,长颈鹿16分钟跑多少千米?
29.
时间/时
1
2
3
4
5
6
…
路程/千米
90
…
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成
比例,理由是
.
③利用图象估计一下,2.5时行
千米,行675千米需要
小时.
五.解答题(共4小题)
30.用一辆汽车运送一批货物,请完成下表.
载重(吨)
4
6
10
12
15
20
运送次数(次)
30
20
(1)运送货物的质量一定,运送的次数与汽车载重的吨数成什么比例?
(2)如果载重为30吨的大货车运送这批货物,几次可以运完?
31.一列客车和一列货车同时从甲乙两站相向开出,客车与货车速度比是3:2,客车行驶6小时到达乙站,货车行驶多少小时到达甲站?
32.两根同样长的钢筋,其中一根锯成3段用了12分钟,另一根要锯成6段,需要多少分钟?(用比例方法解)
33.配制一种药水,药粉和水的质量比是1:80,4.5千克药粉可配制多少千克的药水?(用比例解)
参考答案与试题解析
一.选择题(共8小题)
1.解:A.x+y=10,x与y的和一定,不符合正比例的意义;
B.y﹣x=10,x与y的差一定,不符合正比例的意义;
C.由y=10x得=,所以x、y比值一定,x与y成正比例,符合题意;
故选:C.
2.解:因为,方砖的面积×方砖的块数=铺地的面积(一定),
所以,每块方砖的面积和方砖的块数成反比例,
故选:B。
3.解:A:正方形的面积和它的边长不成比例;
B:路程一定,就是速度和时间的乘积一定,所以行驶的速度和时间成反比例;
C:单价一定,就是总价和数量的比值一定,所以购买商品的数量和总价成正比例;
D:圆柱的底面积和体积不成比例。
故选:C。
4.解:如果x=y,即x:y=(一定),是比值一定,那么x与y成正比例。
故选:A。
5.解:A.圆的面积=π×圆的半径2,不符合正比例的意义,
所以圆的半径和圆的面积不成正比例关系;
B.因为写字总时间=写字总数×写一个字所用时间,
所以写字总时间÷写一个字所用时间=写字总数(一定)符合正比例的意义,写字总数一定,写一个字所用时间和写字总时间成正比例关系;
C.因为每分钟写字个数×写字总时间=写字总数(一定),符合反比例的意义,不符合正比例的意义,
所以写字总数一定,每分钟写字个数和写字总时间不成正比例关系;
D.两个互相咬合的齿轮,齿轮的齿数是一定的与转数没关系,不符合正比例的意义,
所以两个互相咬合的齿轮,齿轮的齿数和转数不成正比例关系,
故选:B。
6.解:路程÷时间=速度(一定),
路程和时间成正比例关系,
图像是:。
故选:C。
7.解;出勤人数=出勤率×全班人数(一定),是比值一定,故出勤人数和出勤率成比例.
故选:A。
8.解:根据长方形的面积公式,长×宽=长方形的面积(一定),符合反比例的意义xy=k(一定),所以长方形的面积一定,长和宽成反比例.
故选:B。
二.填空题(共8小题)
9.解:240÷60=4(小时);
240×2÷(240÷40+4);
=480÷(6+4);
=480÷10;
=48(千米);
答:王飞往返的平均速度是每小时行48千米.
10.解:设乙数为x,
则5:3=60:x,
5x=180,
x=36.
故答案为:36.
11.解:因为y=5x,所以y:x=5(一定),是比值一定,x和y成正比例.
故答案为:正.
12.解:已知xy=5,y与x成反比例
4.2米80厘米=500厘米
3600mL=3.6L
6千克50克=6.05千克
7平方米=700平方分米
故答案为:反;500;3.6;6.05;700。
13.解:(1)1:2=2:4=3:6
设这个物体的质量是x千克。
(12.8﹣8):x=1:2
4.8:x=1:2
x=4.8×2
x=9.6
答:这个物体质量是9.6千克。
(2)弹簧伸长了y厘米。
y:n=1:2
2y=n
2y÷2=n÷2
y=n
(n+8)厘米就是弹簧的长度
答:弹簧长度是(n+8)厘米。
故答案为:9.6,(
n+8)。
14.解:设一长方形被一条直线分成两个长方形的宽分别是a和b,则a:b=1:3,
b=3a,大长方形的宽是a+b=b+b=b,
设长方形的长是c,则cb×=1,
所以cb=2(平方厘米),
原长方形的面积是:c×(a+b)=c×b=bc=×2=(平方厘米);
故答案为:.
15.解:(1)甲车4分钟行驶4千米,乙车4分钟行驶2千米,
4﹣2=2(千米);
答:出发4分钟后,甲、乙两车相距2千米.
(2)从图中可以看出,甲车的速度是1千米/分;
(3)从图中可以看出,甲车行驶6千米,用6分钟;乙车行驶6千米,用12分钟,
12﹣6=6(分钟);
答:甲车比乙车少用6分钟.
(4)根据乙车4分钟行驶2千米,
8÷(2÷4)
=8÷0.5
=16(分钟);
答:乙车在速度不变的情况下从A地行驶到B地一共需要16分钟.
(5)8÷8=1(小时)
12÷6=2(小时)
2﹣1=1(小时)
8×1=8(千米)
答:甲、乙两车相距8千米.
故答案为:2;1;6;16;8.
16.解:笔的枝数×笔的单价=10元钱(一定),是乘积一定,
所以买笔的枝数与笔的单价就成反比例.
故答案为:正确.
三.判断题(共5小题)
17.解:人的身高和体重虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例;
故答案为:×.
18.解:因为图上距离:实际距离=比例尺一定,
所以在同一幅地图上,图上距离与实际距离成正比例,
故在同一幅地图上,图上距离越大实际距离就越大.
故答案为:√.
19.解:每组的人数×组数=六二班的总人数(一定),是乘积一定,每组的人数与组数就成反比例.
故判断为:正确.
20.解:比例尺l:100说明图上的1厘米表示实际的距离100厘米.
故答案为:×
21.解:因为工作总量÷工作效率=工作时间(一定),
比值一定,所以工作时间一定,工作总量和工作效率成正比例;
原题说法正确。
故答案为:√。
四.应用题(共8小题)
22.解:350÷(5﹣3)
=350÷2
=175(棵)
175×3=525(棵)
175×5=875(棵)
答:基地里的樱桃树525棵,苹果树875棵。
23.解:设笑笑收集了x张邮票,
3:5=36:x
3x=5×36
x=
x=60.
答:笑笑收集了60张邮票.
24.解:420×40%=168(棵)
(420﹣168)÷(11+10)
=252÷21
=12(棵)
12×11=132(棵)
12×10=120(棵)
答:甲班植树168棵,乙班植树132棵,丙班植树120棵。
25.解:(1)甲:0.4÷1=0.8÷2=1.2÷3=0.4,即总价÷数量=单价(一定),所以甲种练习本的数量和总价成正比例;
乙:0.4÷2=0.8÷4=1.2÷6=0.2,即总价÷数量=单价(一定),所以乙种练习本的数量和总价成正比例.
(2)5本甲种练习本对应的价钱大约是2元
2.8元与甲种练习本对应的数量是7
答:5本乙种练习本的价钱是1元,2.8元可以买,7本甲种练习本.
(3)从图上看,1本书对应的本数的乙的单价低,所以乙种练习本便宜些.
3.2÷8=0.4(元/本)
2.4÷12=0.2(元/本)
2.4÷0.4=6(本)
2.4÷0.2=12(本)
答:乙种练习本便宜.2.4元可以买6本甲或12本乙练习本.
26.解:设他的影子长多x米。
12:15=1.6:x
12x=15×1.6
12x÷12=15×1.6÷12
x=2
答:他的影子长2米。
27.解:设提前x天完成任务。
120×12=120×(1+20%)×(12﹣x)
120×12=120×120%×(12﹣x)
1440=144×(12﹣x)
1440÷144=144×(12﹣x)÷144
10=12﹣x
10+x=12﹣x+x
10+x=12
10+x﹣10=12﹣10
x=2
答:这样可以提前2天完成。
28.解:(1)因为=速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,
=
5x=4×16
x=
x=12.8
答:长颈鹿16分钟跑12.8千米.
故答案为:正.
29.解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时
1
2
3
4
5
6
…
路程/千米
90
180
270
360
450
540
…
②时间和路程成
正比例,理由是
路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行
225千米,行675千米需要
7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
五.解答题(共4小题)
30.解:4×30=120(吨)
120÷10=12(次)
120÷12=10(次)
120÷15=8(次)
120÷20=6(次)
填表如下:
载重(吨)
4
6
10
12
15
20
运送次数(次)
30
20
12
10
8
6
(1)因为汽车的载重量×运送的次数=这批货物的总质量(一定),所以运送的次数与汽车载重的吨数成反比例.
(2)设x次可以运完,
30x=4×30
x=
x=4
答:4次可以运完.
31.解:设货车行驶x小时到达.
2x=3×6
x=18÷2
x=9
答:货车行驶9小时到达.
32.解:3﹣1=2
6﹣1=5
另一根要锯成6段,需要x分钟,
12:2=x:5
2x=12×5
x=60÷2
x=30;
答:另一根要锯成6段,需要30分钟.
33.解:设可配制x千克的药水.那么水的质量为(x﹣4.5)千克,根据题意可得
4.5:(x﹣4.5)=1:80
解得x=364.5
答:可配制364.5千克的药水.
正比例和反比例》单元测试题
一.选择题(共8小题)
1.表示x和y成正比例关系的式子是( )
A.x+y=10
B.x﹣y=10
C.y=10x
2.铺地面积一定,( )和用砖块数成反比例.
A.每块砖的边长
B.每块砖的面积
C.每块砖的周长
3.下列两种相关联的量,成正比例的是( )
A.正方形的面积和它的边长
B.路程一定,行驶的速度和时间
C.单价一定,购买商品的数量和总价
D.圆柱的底面积和体积
4.如果x=y,那么x与y成( )比例。
A.正
B.反
C.不成
D.无法确定
5.下列两种量的关系成正比例关系的是( )
A.圆的半径和圆的面积
B.写字总数一定,写一个字所用时间和写字总时间
C.写字总数一定,每分钟写字个数和写字总时间
D.两个互相咬合的齿轮,齿轮的齿数和转数
6.下面图中表示淘气爸爸在高速路上某段路程匀速行驶的是( )
A.
B.
C.
D.
7.全班人数一定,出勤人数和出勤率( )
A.成正比例
B.成反比例
C.不成比例
8.长方形的面积一定,长和宽( )
A.成正比例
B.成反比例
C.不成比例
二.填空题(共8小题)
9.王飞以每小时40千米的速度行了240千米,按原路返回时每小时行60千米,王飞往返的平均速度是每小时行
千米.
10.甲数与乙数的比例为5:3,甲数为60,乙数为
.
11.如果y=5x,那么x和y成
比例.
12.已知xy=5,y与x成
比例。
4.2米80厘米=
厘米
3600mL=
L
6千克50克=
千克
7平方米=
平方分米
13.科技小组制作弹簧秤,弹簧长度与所挂砝码质量存在如下关系(在弹簧弹性承受范围内):
弹簧长度/cm
8
9
10
11
……
kg砝码质量/
0
2
4
6
……
(1)用该弹簧秤称一个物体,弹簧长度是12.8厘米,这个物体质量是
千克。
(2)当所称物体质量为n千克,弹簧长度是
厘米。
14.如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1:3,若阴影三角形面积为1平方厘米,则原长方形面积为
平方厘米.
15.如图的统计图表示甲、乙两车同时从A地出发驶向B地的行驶时间和路程情况.请根据图回答以下问题:
(1)出发4分钟后,甲、乙两车相距
千米.
(2)甲车的速度是
千米/分.
(3)行驶6千米的路程,甲车比乙车少用
分钟.
(4)如图中表示甲车已经到达B地,那么乙车在速度不变的情况下从A地行驶到B地一共需要
分钟.
(5)如果甲车到达目的地后立即返回,则当乙车到达目的地时,甲、乙两车相距
千米.
16.小明只有10元钱,他买笔的枝数与笔的单价成反比例.
.
三.判断题(共5小题)
17.人的身高和体重成正比例.
.(判断对错)
18.在同一幅地图上,图上距离越大实际距离就越大.
.(判断对错)
19.六二班的人数一定,每组的人数与组数成反比例.
.(判断对错)
20.比例尺l:100说明图上的1厘米表示实际的距离100米.
.(判断对错)
21.工作时间一定,工作效率与工作总量成正比例。
(判断对错)
四.应用题(共8小题)
22.农业基地里的樱桃树比苹果树少350棵,樱桃树与苹果树的棵数比是3:5,基地里的樱桃树和苹果树各有多少棵?
23.淘气和笑笑收集的邮票张数的比是3:5.淘气收集了36张邮票,笑笑收集了多少张邮票?【用比例解】
24.六年级三个班的学生共植树420棵。甲班植的棵数是总数的40%,乙、丙两班植的棵数的比为11:10。三个班各植树多少棵?
25.如图的图象反映的是购买两种练习本的数量和总价的变化情况.
(1)购买甲种练习本的数量和总价是否成正比例?乙种呢?
(2)估计一下,买5本甲种练习本多少元?2.8元可以买几本甲种练习本?
(3)从图上看哪种练习本便宜些?2.4元可以买两种练习本各多少本?
26.一棵树高12米,它的影长是15米,如果同一时间地点测得小明的身高是1.6米,他的影子长多少米?(用比例解答)
27.铺设一条煤气管道。计划每天铺设120米,用12天完成任务。由于居民着急使用,上级要求每天多铺20%,这样可以提前几天完成?(用比例的知识解)
28.如图的图象表示长颈鹿的奔跑情况.
(1)长颈鹿的奔跑路程与奔跑时间成
比例关系.
(2)请你计算一下,长颈鹿16分钟跑多少千米?
29.
时间/时
1
2
3
4
5
6
…
路程/千米
90
…
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成
比例,理由是
.
③利用图象估计一下,2.5时行
千米,行675千米需要
小时.
五.解答题(共4小题)
30.用一辆汽车运送一批货物,请完成下表.
载重(吨)
4
6
10
12
15
20
运送次数(次)
30
20
(1)运送货物的质量一定,运送的次数与汽车载重的吨数成什么比例?
(2)如果载重为30吨的大货车运送这批货物,几次可以运完?
31.一列客车和一列货车同时从甲乙两站相向开出,客车与货车速度比是3:2,客车行驶6小时到达乙站,货车行驶多少小时到达甲站?
32.两根同样长的钢筋,其中一根锯成3段用了12分钟,另一根要锯成6段,需要多少分钟?(用比例方法解)
33.配制一种药水,药粉和水的质量比是1:80,4.5千克药粉可配制多少千克的药水?(用比例解)
参考答案与试题解析
一.选择题(共8小题)
1.解:A.x+y=10,x与y的和一定,不符合正比例的意义;
B.y﹣x=10,x与y的差一定,不符合正比例的意义;
C.由y=10x得=,所以x、y比值一定,x与y成正比例,符合题意;
故选:C.
2.解:因为,方砖的面积×方砖的块数=铺地的面积(一定),
所以,每块方砖的面积和方砖的块数成反比例,
故选:B。
3.解:A:正方形的面积和它的边长不成比例;
B:路程一定,就是速度和时间的乘积一定,所以行驶的速度和时间成反比例;
C:单价一定,就是总价和数量的比值一定,所以购买商品的数量和总价成正比例;
D:圆柱的底面积和体积不成比例。
故选:C。
4.解:如果x=y,即x:y=(一定),是比值一定,那么x与y成正比例。
故选:A。
5.解:A.圆的面积=π×圆的半径2,不符合正比例的意义,
所以圆的半径和圆的面积不成正比例关系;
B.因为写字总时间=写字总数×写一个字所用时间,
所以写字总时间÷写一个字所用时间=写字总数(一定)符合正比例的意义,写字总数一定,写一个字所用时间和写字总时间成正比例关系;
C.因为每分钟写字个数×写字总时间=写字总数(一定),符合反比例的意义,不符合正比例的意义,
所以写字总数一定,每分钟写字个数和写字总时间不成正比例关系;
D.两个互相咬合的齿轮,齿轮的齿数是一定的与转数没关系,不符合正比例的意义,
所以两个互相咬合的齿轮,齿轮的齿数和转数不成正比例关系,
故选:B。
6.解:路程÷时间=速度(一定),
路程和时间成正比例关系,
图像是:。
故选:C。
7.解;出勤人数=出勤率×全班人数(一定),是比值一定,故出勤人数和出勤率成比例.
故选:A。
8.解:根据长方形的面积公式,长×宽=长方形的面积(一定),符合反比例的意义xy=k(一定),所以长方形的面积一定,长和宽成反比例.
故选:B。
二.填空题(共8小题)
9.解:240÷60=4(小时);
240×2÷(240÷40+4);
=480÷(6+4);
=480÷10;
=48(千米);
答:王飞往返的平均速度是每小时行48千米.
10.解:设乙数为x,
则5:3=60:x,
5x=180,
x=36.
故答案为:36.
11.解:因为y=5x,所以y:x=5(一定),是比值一定,x和y成正比例.
故答案为:正.
12.解:已知xy=5,y与x成反比例
4.2米80厘米=500厘米
3600mL=3.6L
6千克50克=6.05千克
7平方米=700平方分米
故答案为:反;500;3.6;6.05;700。
13.解:(1)1:2=2:4=3:6
设这个物体的质量是x千克。
(12.8﹣8):x=1:2
4.8:x=1:2
x=4.8×2
x=9.6
答:这个物体质量是9.6千克。
(2)弹簧伸长了y厘米。
y:n=1:2
2y=n
2y÷2=n÷2
y=n
(n+8)厘米就是弹簧的长度
答:弹簧长度是(n+8)厘米。
故答案为:9.6,(
n+8)。
14.解:设一长方形被一条直线分成两个长方形的宽分别是a和b,则a:b=1:3,
b=3a,大长方形的宽是a+b=b+b=b,
设长方形的长是c,则cb×=1,
所以cb=2(平方厘米),
原长方形的面积是:c×(a+b)=c×b=bc=×2=(平方厘米);
故答案为:.
15.解:(1)甲车4分钟行驶4千米,乙车4分钟行驶2千米,
4﹣2=2(千米);
答:出发4分钟后,甲、乙两车相距2千米.
(2)从图中可以看出,甲车的速度是1千米/分;
(3)从图中可以看出,甲车行驶6千米,用6分钟;乙车行驶6千米,用12分钟,
12﹣6=6(分钟);
答:甲车比乙车少用6分钟.
(4)根据乙车4分钟行驶2千米,
8÷(2÷4)
=8÷0.5
=16(分钟);
答:乙车在速度不变的情况下从A地行驶到B地一共需要16分钟.
(5)8÷8=1(小时)
12÷6=2(小时)
2﹣1=1(小时)
8×1=8(千米)
答:甲、乙两车相距8千米.
故答案为:2;1;6;16;8.
16.解:笔的枝数×笔的单价=10元钱(一定),是乘积一定,
所以买笔的枝数与笔的单价就成反比例.
故答案为:正确.
三.判断题(共5小题)
17.解:人的身高和体重虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例;
故答案为:×.
18.解:因为图上距离:实际距离=比例尺一定,
所以在同一幅地图上,图上距离与实际距离成正比例,
故在同一幅地图上,图上距离越大实际距离就越大.
故答案为:√.
19.解:每组的人数×组数=六二班的总人数(一定),是乘积一定,每组的人数与组数就成反比例.
故判断为:正确.
20.解:比例尺l:100说明图上的1厘米表示实际的距离100厘米.
故答案为:×
21.解:因为工作总量÷工作效率=工作时间(一定),
比值一定,所以工作时间一定,工作总量和工作效率成正比例;
原题说法正确。
故答案为:√。
四.应用题(共8小题)
22.解:350÷(5﹣3)
=350÷2
=175(棵)
175×3=525(棵)
175×5=875(棵)
答:基地里的樱桃树525棵,苹果树875棵。
23.解:设笑笑收集了x张邮票,
3:5=36:x
3x=5×36
x=
x=60.
答:笑笑收集了60张邮票.
24.解:420×40%=168(棵)
(420﹣168)÷(11+10)
=252÷21
=12(棵)
12×11=132(棵)
12×10=120(棵)
答:甲班植树168棵,乙班植树132棵,丙班植树120棵。
25.解:(1)甲:0.4÷1=0.8÷2=1.2÷3=0.4,即总价÷数量=单价(一定),所以甲种练习本的数量和总价成正比例;
乙:0.4÷2=0.8÷4=1.2÷6=0.2,即总价÷数量=单价(一定),所以乙种练习本的数量和总价成正比例.
(2)5本甲种练习本对应的价钱大约是2元
2.8元与甲种练习本对应的数量是7
答:5本乙种练习本的价钱是1元,2.8元可以买,7本甲种练习本.
(3)从图上看,1本书对应的本数的乙的单价低,所以乙种练习本便宜些.
3.2÷8=0.4(元/本)
2.4÷12=0.2(元/本)
2.4÷0.4=6(本)
2.4÷0.2=12(本)
答:乙种练习本便宜.2.4元可以买6本甲或12本乙练习本.
26.解:设他的影子长多x米。
12:15=1.6:x
12x=15×1.6
12x÷12=15×1.6÷12
x=2
答:他的影子长2米。
27.解:设提前x天完成任务。
120×12=120×(1+20%)×(12﹣x)
120×12=120×120%×(12﹣x)
1440=144×(12﹣x)
1440÷144=144×(12﹣x)÷144
10=12﹣x
10+x=12﹣x+x
10+x=12
10+x﹣10=12﹣10
x=2
答:这样可以提前2天完成。
28.解:(1)因为=速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,
=
5x=4×16
x=
x=12.8
答:长颈鹿16分钟跑12.8千米.
故答案为:正.
29.解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时
1
2
3
4
5
6
…
路程/千米
90
180
270
360
450
540
…
②时间和路程成
正比例,理由是
路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行
225千米,行675千米需要
7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
五.解答题(共4小题)
30.解:4×30=120(吨)
120÷10=12(次)
120÷12=10(次)
120÷15=8(次)
120÷20=6(次)
填表如下:
载重(吨)
4
6
10
12
15
20
运送次数(次)
30
20
12
10
8
6
(1)因为汽车的载重量×运送的次数=这批货物的总质量(一定),所以运送的次数与汽车载重的吨数成反比例.
(2)设x次可以运完,
30x=4×30
x=
x=4
答:4次可以运完.
31.解:设货车行驶x小时到达.
2x=3×6
x=18÷2
x=9
答:货车行驶9小时到达.
32.解:3﹣1=2
6﹣1=5
另一根要锯成6段,需要x分钟,
12:2=x:5
2x=12×5
x=60÷2
x=30;
答:另一根要锯成6段,需要30分钟.
33.解:设可配制x千克的药水.那么水的质量为(x﹣4.5)千克,根据题意可得
4.5:(x﹣4.5)=1:80
解得x=364.5
答:可配制364.5千克的药水.
