2020-2021学年苏教版小学六年级数学下册《第六章 正比例和反比例》单元测试题(有答案)
文档属性
| 名称 | 2020-2021学年苏教版小学六年级数学下册《第六章 正比例和反比例》单元测试题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 193.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 00:00:00 | ||
图片预览




文档简介
2020-2021学年苏教版小学六年级数学下册《第六章
正比例和反比例》单元测试题
一.选择题(共8小题)
1.正方形的边长和它的周长( )
A.成正比例
B.成反比例
C.不成比例
2.下列几种量中,不是成反比例的量是( )
A.路程一定,速度和时间
B.减数一定,被减数和差
C.面积一定,平行四边形的底和高
3.下列各种关系中,成反比例关系的是( )
A.甲数和乙数的商是8,甲数和乙数
B.在一定时间里,每分钟生产的零件个数和生产零件的总个数
C.三角形面积一定,它的底和高
D.圆的面积一定,它的半径和圆周率
4.全班人数一定,出勤人数与缺勤人数( )
A.成正比例
B.成反比例
C.不成比例
5.一袋纯牛奶1.50元,购买纯牛奶的袋数和总钱数( )
A.成正比例
B.成反比例
C.不成比例
6.下列图象表示正比例关系的是( )
A.
B.
C.
D.
7.圆的周长和直径( )
A.成正比例
B.成反比例
C.不成比例
8.总价一定,单价和数量( )
A.成正比例
B.成反比例
C.不成比例
D.以上都不对
二.填空题(共8小题)
9.陈明所在学校的田径场长120米,如果按1:2000的比例画到图纸上,需要画
厘米.
10.甲、乙两个容积相同的瓶子分别装满盐水,已知甲瓶中盐、水的比是2:9,乙瓶中盐与水的比是3:10,现在把甲、乙两瓶盐水混合在一起,则盐水中盐与盐水的比是
.
11.少先队员每人做好事的件数一定,做好事的总件数与做好事的少先队员人数成正比例.
.
12.在ab=c(a、b、c均不为0)中,当b一定时,a和c成
比例;当c一定时,a和b成
比例.
13.如图,在平衡架的左侧已挂上了3个砝码,每个30克。在右边第5格处必须挂
克砝码,才能使平衡架平衡。
14.如果在比例尺是1:5000的图纸上,画一个边长为4厘米的正方形草坪图,这个草坪图的实际面积是
平方米.
15.一种练习本销售的数量与总价的关系如表.
数量/本
1
2
3
4
5
总价/元
5.5
11
16.5
22
27.5
(1)表中有
和
两种相关联的量,总价随着
的变化而变化,且总价与相应数量的比值都是
,实际就是练习本的
.
(2)像这样,两种
的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的
一定,这两种量就叫做
的量,它们的关系叫做
关系.上表中,总价和数量是成
的量,总价与数量成
关系.
16.在比例中,两个外项的积一定,两个两内项成
比例.
三.判断题(共5小题)
17.修路的总米数一定,修好了的米数和剩下的米数成正比例.
(判断对错)
18.分数值一定,它的分子和分母成正比例.
.(判断对错)
19.在一定的距离内,车轮周长和它转动的圈数成反比例.
.(判断对错)
20.自行车的前齿轮越大,后齿轮转的圈数越多.
.(判断对错)
21.如果=,那么x与y成正比例。
(判断对错)
四.应用题(共8小题)
22.在比例尺是1:20000000的地图上量得甲、乙两地间的铁路长5厘米.有两列火车分别从甲、乙两地同时相对开出.已知一辆火车平均每小时行驶170千米,另一辆火车平均每小时行驶130千米.大约经过多少小时两车还差95千米相遇.(结果保留两位小数)
23.甲、乙两个筑路队人数的比是7:3.如果从甲队派30人到乙队,则两队的人数比就成了3:2.甲、乙两个筑路队原来各有多少人?(用比例解)
24.疫情期间,昆明王大叔驾车运送物资前往武汉支援。2小时行驶160千米,照这样的速度,昆明到武汉约有1600千米,王大叔需要几小时到达武汉?(用比例解)
25.如图的图象反映的是老虎和狮子的食肉情况.
(1)老虎的食肉量与时间成正比例吗?狮子呢?
(2)估计一下,老虎和狮子8天各食肉多少千克?
(3)哪种动物每天的食肉量较少?
26.小明5分钟可以走325米,照这样计算,从家到学校相距1300米,他要走多少分钟?(用比例解答)
27.某售楼部大厅中央有一个小区微缩景观模型,模型中的2号楼高45厘米,宽10厘米,已知该楼实际高90米,则该楼实际宽多少米?
28.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t
2.5
3
5
10
数量/辆
48
40
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
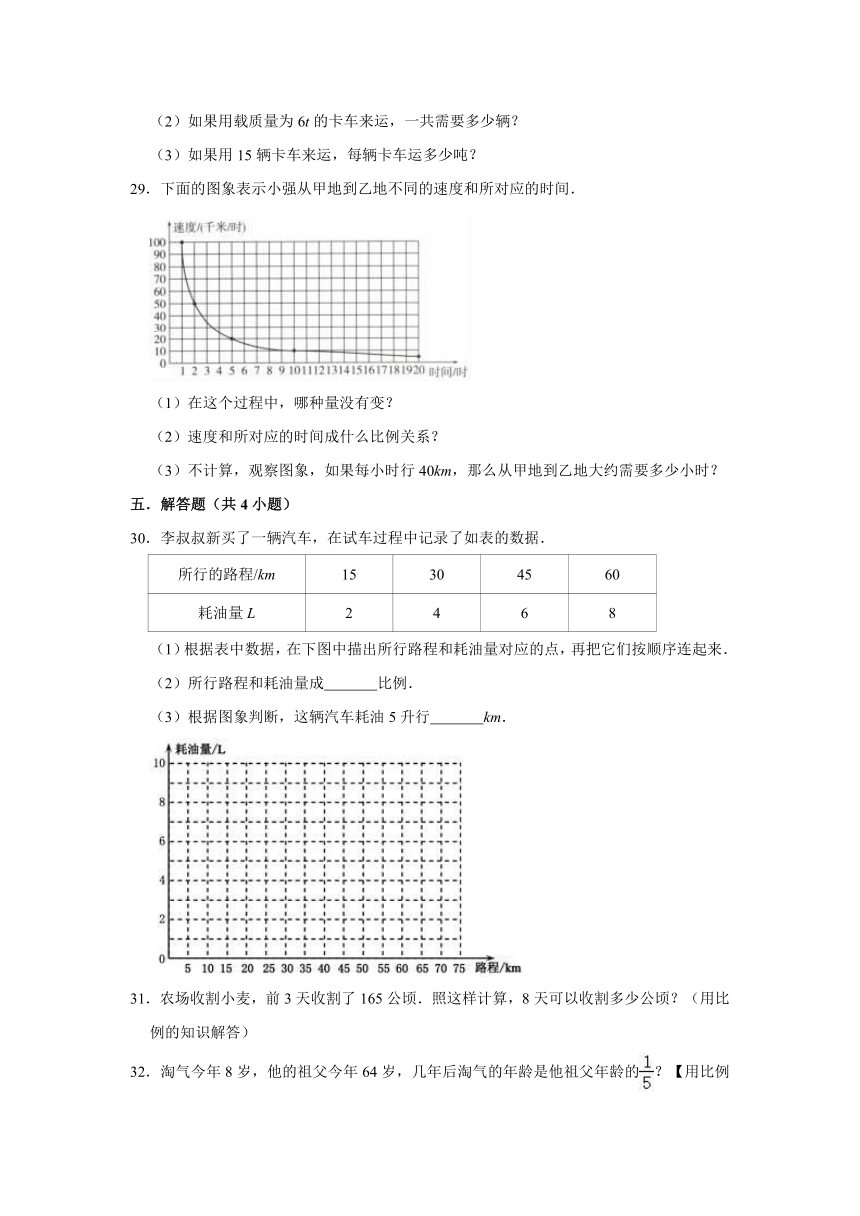
29.下面的图象表示小强从甲地到乙地不同的速度和所对应的时间.
(1)在这个过程中,哪种量没有变?
(2)速度和所对应的时间成什么比例关系?
(3)不计算,观察图象,如果每小时行40km,那么从甲地到乙地大约需要多少小时?
五.解答题(共4小题)
30.李叔叔新买了一辆汽车,在试车过程中记录了如表的数据.
所行的路程/km
15
30
45
60
耗油量L
2
4
6
8
(1)根据表中数据,在下图中描出所行路程和耗油量对应的点,再把它们按顺序连起来.
(2)所行路程和耗油量成
比例.
(3)根据图象判断,这辆汽车耗油5升行
km.
31.农场收割小麦,前3天收割了165公顷.照这样计算,8天可以收割多少公顷?(用比例的知识解答)
32.淘气今年8岁,他的祖父今年64岁,几年后淘气的年龄是他祖父年龄的?【用比例解】
33.50千克花生仁可以榨油19千克.要榨200千克花生油需多少千克花生仁?(比例解)
参考答案与试题解析
一.选择题(共8小题)
1.解:正方形的周长÷边长=4(一定),是比值一定,所以正方形的周长和它的边长成正比例;
故选:A.
2.解:A选项:速度×时间=路程(一定),速度和时间乘积一定,成反比例;
B选项:被减数﹣差=被减数(一定),被减数和差是和与差的关系,乘积和比值都不是一定的,不成任何比例;
C选项:平行四边形的底×高=面积(一定),平行四边形的底和高的乘积一定,成反比例关系.
故选:B。
3.解:A:因为甲数和乙数的比值一定,所以甲数和乙数成正比例;
B:因为时间一定,所以每分钟生产的零件个数和生产零件的总个数成正比例;
C:三角形面积一定,它的底和高成反比例;
D:圆的面积一定,它的半径和圆周率不成比例。
故选:C。
4.解:全出勤人数+缺勤人数=全班人数(一定),是对应的和一定,所以出勤人数与缺勤人数不成比例。
故选:C。
5.解:购买电纯牛奶的钱数÷总袋数=每袋纯牛奶的价格(一定),是比值一定,购买纯牛奶袋数和总钱数成正比例.
故选:A.
6.解:选项A:不是过原点的一条射线,不成正比例关系,故错误;
选项B:不是过原点的一条射线,不成正比例关系,故错误;
选项C:是以原点为端点的一条射线,成正比例关系,故正确;
选项D:不是过原点的一条射线,不成正比例关系,故错误;
故选:C.
7.解:圆的周长公式:C=πd,
可以推出:C:d=π(一定);
圆的周长和直径是两种相关联的量,圆的周长随直径的变化而变化,π一定,也就是圆的周长和对应的直径的比值一定,所以圆的周长和直径是成正比例关系.
故选:A。
8.解:从题中可以得到以下数量关系:
单价×数量=总价(一定),
可以看出,单价和数量是两种相关联的量,单价随数量的变化而变化.总价一定,也就是单价与数量相对应数的乘积一定,符合反比例的意义.所以单价与数量成反比例关系.
故选:B。
二.填空题(共8小题)
9.解:120米=12000厘米,
图上距离:12000×=6(厘米).
答:需要画6厘米.
10.解:甲瓶盐含量:2÷(2+9)=
水含量:9÷(2+9)=
乙瓶盐含量:3÷(3+10)=,
水含量:10÷(3+10)=;
两瓶混合盐含量:
+=,
水含量:,
盐:水==59:227;
盐:盐水=59:(59+227)=59:286;
故答案为:59:286.
11.解:做好事的总件数÷做好事的少先队员人数=每人做好事的件数(一定),是比值一定,所以成正比例;
故答案为:√.
12.解:因为ab=c,即c:a=b(一定),比值一定,所以a和c成正比例;
因为ab=c(一定),乘积一定,所以a和b成反比例;
故答案为:正、反.
13.解:设在右边第5格处必须挂x克砝码,才能使平衡架平衡。
5x=(30×3)×3
5x=270
5x÷5=270÷5
x=54
答:在右边第5格处必须挂54克砝码,才能使平衡架平衡。
故答案为:54。
14.解:设正方形的实际边长是x厘米,
1:5000=4:x
x=5000×4
x=20000;
20000厘米=200米;
面积是:200×200=40000(平方米)
答:这个草坪图的实际面积是40000平方米.
故答案为:40000.
15.解:(1)5.5:1=5.5
11:2=5.5
16.5:3=5.5
22:4=5.5
27.5:5=5.5
表中有总价和数量两种相关联的量,总价随着数量的变化而变化,且总价与相应数量的比值都是一定的,实际就是练习本的单价.
(2)像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.上表中,总价和数量是成正比例的量,总价与数量成正比例关系.
故答案为:总价,数量,数量,一定的,单价,相关联,比值,正比例,正比例,正比例,正比例.
16.解:内项×内项=外项×外项(一定),
可以看出,两内项是两种相关联的量,一内项随另一内项的变化而变化,
两外项的积一定,也就是两内项相对应数的乘积一定,所以两内项成反比例关系.
故答案为:反.
三.判断题(共5小题)
17.解:修好了的米数+剩下的米数=修路的总米数(一定),是和一定,不是比值或乘积一定,所以不成比例;
故答案为:×.
18.解:=分数值(一定),是比值一定,分子和分母成正比例.
故判断为:正确.
19.解:车轮周长×它转动的圈数=距离(一定),是乘积一定,车轮周长和它转动的圈数就成反比例.
故判断为:正确.
20.解:根据前齿轮的齿数×前齿轮的圈数=后齿轮的齿数×后齿轮的圈数,可得齿轮转的圈数与齿轮的齿数的多少有关,与大小无关,
所以本题说法错误,
故答案为:×.
21.解:因为=,
则xy=25(一定),
所以y和x成反比例;原题说法错误。
故答案为:×。
四.应用题(共8小题)
22.解:5÷=100000000(厘米)
100000000厘米=1000千米
(1000﹣95)÷(170+130)
=905÷300
≈3.02(小时)
答:大约经过3.02小时两车还差95千米相遇。
23.解:设原来甲队有7x人,乙队3x人,
(7x﹣30):(3x+30)=3:2
2(7x﹣30)=3(3x+30)
14x﹣60=9x+90
5x=150
x=30
30×7=210(人)
30×3=90(人)
答:甲筑路队原来有210人,乙筑路队原来有90人.
24.解:设王大叔需要x小时到达武汉。
1600:x=160:2
160x=1600×2
160x÷160=1600×2÷160
x=20
答:王大叔需要20小时到达武汉。
25.解:(1)答:老虎的食肉量与所用时间是成正比例;狮子的食肉量与所用时间是成正比例.
(2)如图
答:老虎9天可以吃约36千克肉,狮子9天吃约60千克肉.
(3)33÷8≈4(千克)
53÷8≈6(千克)
6>4
答:狮子每天的食肉量多.
26.解:设他需要走x分钟。
1300:x=325:5
325x=1300×5
325x÷325=1300×5÷325
x=20
答:他要走20分钟。
27.解:设该楼实际宽x米。
10:x=45:90
45x=10×90
45x÷45=10×90÷45
x=20
答:该楼实际宽20米。
28.解:3×40÷5
=120÷5
=24(辆)
3×40÷10
=120÷10
=12(辆)
载质量/t
2.5
3
5
10
数量/辆
48
40
24
12
(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,
所以车辆的载重量与所需车辆的数量成反比例.
(2)120÷5=24(辆)
答:用载重量6吨的卡车来运,一共需要24辆.
(3)120÷15=8(吨)
答:每辆卡车运8吨.
故答案为:24;12.
29.解:(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化.
(2)观察图象发现速度和时间的关系是反比例关系.
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时.
五.解答题(共4小题)
30.解:(1)画图如下:
(2)15÷2=30÷4=45÷6=60÷8=7.5(一定),即:汽车行驶的路程÷耗油量=每升油行驶的路程(一定),
所以这辆汽车行驶的路程和耗油量成正比例.
(3)观察图表,这辆汽车耗油5升行37.5km.
故答案为:正,37.5.
31.解:设8天可以收割x公顷,
165:3=x:8,
3x=165×8,
x=440,
答:8天可以收割440公顷.
32.解:设x年后淘气的年龄是他祖父年龄的,
=
(8+x)×5=64+x
40+5x=64+x
40+4x=64
4x=64﹣40
4x=24
x=6.
答:6年后淘气的年龄是他祖父年龄的.
33.解:设榨200千克花生油需x千克花生仁,由此可得比例:
50:19=x:200,
19x=10000,
x≈526.32;
答:大约需要526.32千克花生仁.
正比例和反比例》单元测试题
一.选择题(共8小题)
1.正方形的边长和它的周长( )
A.成正比例
B.成反比例
C.不成比例
2.下列几种量中,不是成反比例的量是( )
A.路程一定,速度和时间
B.减数一定,被减数和差
C.面积一定,平行四边形的底和高
3.下列各种关系中,成反比例关系的是( )
A.甲数和乙数的商是8,甲数和乙数
B.在一定时间里,每分钟生产的零件个数和生产零件的总个数
C.三角形面积一定,它的底和高
D.圆的面积一定,它的半径和圆周率
4.全班人数一定,出勤人数与缺勤人数( )
A.成正比例
B.成反比例
C.不成比例
5.一袋纯牛奶1.50元,购买纯牛奶的袋数和总钱数( )
A.成正比例
B.成反比例
C.不成比例
6.下列图象表示正比例关系的是( )
A.
B.
C.
D.
7.圆的周长和直径( )
A.成正比例
B.成反比例
C.不成比例
8.总价一定,单价和数量( )
A.成正比例
B.成反比例
C.不成比例
D.以上都不对
二.填空题(共8小题)
9.陈明所在学校的田径场长120米,如果按1:2000的比例画到图纸上,需要画
厘米.
10.甲、乙两个容积相同的瓶子分别装满盐水,已知甲瓶中盐、水的比是2:9,乙瓶中盐与水的比是3:10,现在把甲、乙两瓶盐水混合在一起,则盐水中盐与盐水的比是
.
11.少先队员每人做好事的件数一定,做好事的总件数与做好事的少先队员人数成正比例.
.
12.在ab=c(a、b、c均不为0)中,当b一定时,a和c成
比例;当c一定时,a和b成
比例.
13.如图,在平衡架的左侧已挂上了3个砝码,每个30克。在右边第5格处必须挂
克砝码,才能使平衡架平衡。
14.如果在比例尺是1:5000的图纸上,画一个边长为4厘米的正方形草坪图,这个草坪图的实际面积是
平方米.
15.一种练习本销售的数量与总价的关系如表.
数量/本
1
2
3
4
5
总价/元
5.5
11
16.5
22
27.5
(1)表中有
和
两种相关联的量,总价随着
的变化而变化,且总价与相应数量的比值都是
,实际就是练习本的
.
(2)像这样,两种
的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的
一定,这两种量就叫做
的量,它们的关系叫做
关系.上表中,总价和数量是成
的量,总价与数量成
关系.
16.在比例中,两个外项的积一定,两个两内项成
比例.
三.判断题(共5小题)
17.修路的总米数一定,修好了的米数和剩下的米数成正比例.
(判断对错)
18.分数值一定,它的分子和分母成正比例.
.(判断对错)
19.在一定的距离内,车轮周长和它转动的圈数成反比例.
.(判断对错)
20.自行车的前齿轮越大,后齿轮转的圈数越多.
.(判断对错)
21.如果=,那么x与y成正比例。
(判断对错)
四.应用题(共8小题)
22.在比例尺是1:20000000的地图上量得甲、乙两地间的铁路长5厘米.有两列火车分别从甲、乙两地同时相对开出.已知一辆火车平均每小时行驶170千米,另一辆火车平均每小时行驶130千米.大约经过多少小时两车还差95千米相遇.(结果保留两位小数)
23.甲、乙两个筑路队人数的比是7:3.如果从甲队派30人到乙队,则两队的人数比就成了3:2.甲、乙两个筑路队原来各有多少人?(用比例解)
24.疫情期间,昆明王大叔驾车运送物资前往武汉支援。2小时行驶160千米,照这样的速度,昆明到武汉约有1600千米,王大叔需要几小时到达武汉?(用比例解)
25.如图的图象反映的是老虎和狮子的食肉情况.
(1)老虎的食肉量与时间成正比例吗?狮子呢?
(2)估计一下,老虎和狮子8天各食肉多少千克?
(3)哪种动物每天的食肉量较少?
26.小明5分钟可以走325米,照这样计算,从家到学校相距1300米,他要走多少分钟?(用比例解答)
27.某售楼部大厅中央有一个小区微缩景观模型,模型中的2号楼高45厘米,宽10厘米,已知该楼实际高90米,则该楼实际宽多少米?
28.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t
2.5
3
5
10
数量/辆
48
40
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
29.下面的图象表示小强从甲地到乙地不同的速度和所对应的时间.
(1)在这个过程中,哪种量没有变?
(2)速度和所对应的时间成什么比例关系?
(3)不计算,观察图象,如果每小时行40km,那么从甲地到乙地大约需要多少小时?
五.解答题(共4小题)
30.李叔叔新买了一辆汽车,在试车过程中记录了如表的数据.
所行的路程/km
15
30
45
60
耗油量L
2
4
6
8
(1)根据表中数据,在下图中描出所行路程和耗油量对应的点,再把它们按顺序连起来.
(2)所行路程和耗油量成
比例.
(3)根据图象判断,这辆汽车耗油5升行
km.
31.农场收割小麦,前3天收割了165公顷.照这样计算,8天可以收割多少公顷?(用比例的知识解答)
32.淘气今年8岁,他的祖父今年64岁,几年后淘气的年龄是他祖父年龄的?【用比例解】
33.50千克花生仁可以榨油19千克.要榨200千克花生油需多少千克花生仁?(比例解)
参考答案与试题解析
一.选择题(共8小题)
1.解:正方形的周长÷边长=4(一定),是比值一定,所以正方形的周长和它的边长成正比例;
故选:A.
2.解:A选项:速度×时间=路程(一定),速度和时间乘积一定,成反比例;
B选项:被减数﹣差=被减数(一定),被减数和差是和与差的关系,乘积和比值都不是一定的,不成任何比例;
C选项:平行四边形的底×高=面积(一定),平行四边形的底和高的乘积一定,成反比例关系.
故选:B。
3.解:A:因为甲数和乙数的比值一定,所以甲数和乙数成正比例;
B:因为时间一定,所以每分钟生产的零件个数和生产零件的总个数成正比例;
C:三角形面积一定,它的底和高成反比例;
D:圆的面积一定,它的半径和圆周率不成比例。
故选:C。
4.解:全出勤人数+缺勤人数=全班人数(一定),是对应的和一定,所以出勤人数与缺勤人数不成比例。
故选:C。
5.解:购买电纯牛奶的钱数÷总袋数=每袋纯牛奶的价格(一定),是比值一定,购买纯牛奶袋数和总钱数成正比例.
故选:A.
6.解:选项A:不是过原点的一条射线,不成正比例关系,故错误;
选项B:不是过原点的一条射线,不成正比例关系,故错误;
选项C:是以原点为端点的一条射线,成正比例关系,故正确;
选项D:不是过原点的一条射线,不成正比例关系,故错误;
故选:C.
7.解:圆的周长公式:C=πd,
可以推出:C:d=π(一定);
圆的周长和直径是两种相关联的量,圆的周长随直径的变化而变化,π一定,也就是圆的周长和对应的直径的比值一定,所以圆的周长和直径是成正比例关系.
故选:A。
8.解:从题中可以得到以下数量关系:
单价×数量=总价(一定),
可以看出,单价和数量是两种相关联的量,单价随数量的变化而变化.总价一定,也就是单价与数量相对应数的乘积一定,符合反比例的意义.所以单价与数量成反比例关系.
故选:B。
二.填空题(共8小题)
9.解:120米=12000厘米,
图上距离:12000×=6(厘米).
答:需要画6厘米.
10.解:甲瓶盐含量:2÷(2+9)=
水含量:9÷(2+9)=
乙瓶盐含量:3÷(3+10)=,
水含量:10÷(3+10)=;
两瓶混合盐含量:
+=,
水含量:,
盐:水==59:227;
盐:盐水=59:(59+227)=59:286;
故答案为:59:286.
11.解:做好事的总件数÷做好事的少先队员人数=每人做好事的件数(一定),是比值一定,所以成正比例;
故答案为:√.
12.解:因为ab=c,即c:a=b(一定),比值一定,所以a和c成正比例;
因为ab=c(一定),乘积一定,所以a和b成反比例;
故答案为:正、反.
13.解:设在右边第5格处必须挂x克砝码,才能使平衡架平衡。
5x=(30×3)×3
5x=270
5x÷5=270÷5
x=54
答:在右边第5格处必须挂54克砝码,才能使平衡架平衡。
故答案为:54。
14.解:设正方形的实际边长是x厘米,
1:5000=4:x
x=5000×4
x=20000;
20000厘米=200米;
面积是:200×200=40000(平方米)
答:这个草坪图的实际面积是40000平方米.
故答案为:40000.
15.解:(1)5.5:1=5.5
11:2=5.5
16.5:3=5.5
22:4=5.5
27.5:5=5.5
表中有总价和数量两种相关联的量,总价随着数量的变化而变化,且总价与相应数量的比值都是一定的,实际就是练习本的单价.
(2)像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.上表中,总价和数量是成正比例的量,总价与数量成正比例关系.
故答案为:总价,数量,数量,一定的,单价,相关联,比值,正比例,正比例,正比例,正比例.
16.解:内项×内项=外项×外项(一定),
可以看出,两内项是两种相关联的量,一内项随另一内项的变化而变化,
两外项的积一定,也就是两内项相对应数的乘积一定,所以两内项成反比例关系.
故答案为:反.
三.判断题(共5小题)
17.解:修好了的米数+剩下的米数=修路的总米数(一定),是和一定,不是比值或乘积一定,所以不成比例;
故答案为:×.
18.解:=分数值(一定),是比值一定,分子和分母成正比例.
故判断为:正确.
19.解:车轮周长×它转动的圈数=距离(一定),是乘积一定,车轮周长和它转动的圈数就成反比例.
故判断为:正确.
20.解:根据前齿轮的齿数×前齿轮的圈数=后齿轮的齿数×后齿轮的圈数,可得齿轮转的圈数与齿轮的齿数的多少有关,与大小无关,
所以本题说法错误,
故答案为:×.
21.解:因为=,
则xy=25(一定),
所以y和x成反比例;原题说法错误。
故答案为:×。
四.应用题(共8小题)
22.解:5÷=100000000(厘米)
100000000厘米=1000千米
(1000﹣95)÷(170+130)
=905÷300
≈3.02(小时)
答:大约经过3.02小时两车还差95千米相遇。
23.解:设原来甲队有7x人,乙队3x人,
(7x﹣30):(3x+30)=3:2
2(7x﹣30)=3(3x+30)
14x﹣60=9x+90
5x=150
x=30
30×7=210(人)
30×3=90(人)
答:甲筑路队原来有210人,乙筑路队原来有90人.
24.解:设王大叔需要x小时到达武汉。
1600:x=160:2
160x=1600×2
160x÷160=1600×2÷160
x=20
答:王大叔需要20小时到达武汉。
25.解:(1)答:老虎的食肉量与所用时间是成正比例;狮子的食肉量与所用时间是成正比例.
(2)如图
答:老虎9天可以吃约36千克肉,狮子9天吃约60千克肉.
(3)33÷8≈4(千克)
53÷8≈6(千克)
6>4
答:狮子每天的食肉量多.
26.解:设他需要走x分钟。
1300:x=325:5
325x=1300×5
325x÷325=1300×5÷325
x=20
答:他要走20分钟。
27.解:设该楼实际宽x米。
10:x=45:90
45x=10×90
45x÷45=10×90÷45
x=20
答:该楼实际宽20米。
28.解:3×40÷5
=120÷5
=24(辆)
3×40÷10
=120÷10
=12(辆)
载质量/t
2.5
3
5
10
数量/辆
48
40
24
12
(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,
所以车辆的载重量与所需车辆的数量成反比例.
(2)120÷5=24(辆)
答:用载重量6吨的卡车来运,一共需要24辆.
(3)120÷15=8(吨)
答:每辆卡车运8吨.
故答案为:24;12.
29.解:(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化.
(2)观察图象发现速度和时间的关系是反比例关系.
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时.
五.解答题(共4小题)
30.解:(1)画图如下:
(2)15÷2=30÷4=45÷6=60÷8=7.5(一定),即:汽车行驶的路程÷耗油量=每升油行驶的路程(一定),
所以这辆汽车行驶的路程和耗油量成正比例.
(3)观察图表,这辆汽车耗油5升行37.5km.
故答案为:正,37.5.
31.解:设8天可以收割x公顷,
165:3=x:8,
3x=165×8,
x=440,
答:8天可以收割440公顷.
32.解:设x年后淘气的年龄是他祖父年龄的,
=
(8+x)×5=64+x
40+5x=64+x
40+4x=64
4x=64﹣40
4x=24
x=6.
答:6年后淘气的年龄是他祖父年龄的.
33.解:设榨200千克花生油需x千克花生仁,由此可得比例:
50:19=x:200,
19x=10000,
x≈526.32;
答:大约需要526.32千克花生仁.
