2020--2021学年人教版七年级数学下册第7章:平面直角坐标系小结与复习(共27张ppt)
文档属性
| 名称 | 2020--2021学年人教版七年级数学下册第7章:平面直角坐标系小结与复习(共27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 11:04:14 | ||
图片预览






文档简介
(共27张PPT)
平面直角坐标系
章末复习
目录页
讲授新课
当堂练习
课堂小结
新课导入
要点梳理
教学目标
教学重点
1.点与坐标一一对应.
点
坐标
确定
找到
要点梳理
要点梳理
2.象限、坐标符号、坐标轴上的点的坐标特点.
点的位置
横坐标符号
纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴
y轴
+
+
-
+
-
-
+
-
纵坐标为0
横坐标为0
要点梳理
要点梳理
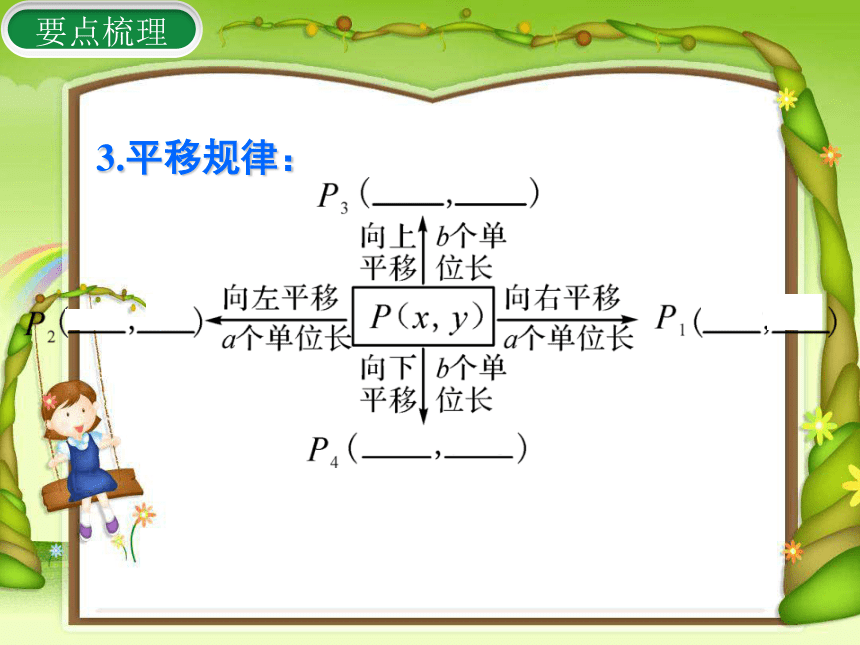
3.平移规律:
要点梳理
要点梳理
4.用坐标表示地理位置:
(1)直角坐标系法
(2)方向角和距离法
考点精讲
典例精讲
归纳总结
考点精讲
考点精讲
考点1
平面直角坐标系与点的坐标
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的
距离为5,则点a的值是
.
【归纳拓展】
1.第一、三象限内点的横、纵坐标同号;
2.第二、四象限内点的横、纵坐标异号;
3.平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的
距离是它横坐标的绝对值;
4.平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线
上的点的横坐标相同.
-2
针对训练
1.已知点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是
______
_________.
2.已知点P在第二象限,且到x轴、y轴的距离分别为2和3,
则P点坐标为
.
或(6,-6)
(3,3)
(-3,2)
考点2
坐标与平移
【例2】如图,把三角形ABC经过一定的变换得到三角形A′B′C′,如果三角形ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为
.
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
(a+3,b+2)
将点(2,-5)向左平移1个单位长度,再向上平移6个单位长度得到点
.
针对训练
(1,1)
向左平移a个单位对应点P2(x-a,y)
总结归纳
向右平移a个单位对应点
P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
典例精析
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8)
B.(1,-2)
C.(-6,-1)
D.(0,-1)
点的平移变换:左右移动改变点的横坐标,左减右
加;上下移动改变点的纵坐标,下减上加.
归纳
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
考点3
平面作图及求坐标系中的几何图形面积
【例3】(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个
单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A(0,2)
B(4,3)
C(3,0)
S=3×4-1/2×2×3-1/2×1×4
-1/2×1×3=5.5
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:(一)通常用割或补的方法将要求图形转化为一些特殊的图形,去间接计算面积.
(二)需要将已知点的坐标转化为线段的长度,以满足求面积的需要.
已知直角三角形ABC的直角边BC=AC,
且B(3,2),C(3,-2),求点A的坐标及三
角形ABC的面积.
A
B
C
O
x
y
解:∵B(3,2),C(3,-2),
∴BC∥y轴,且BC=2-(-2)=4,
∴AC=BC=4.
∴三角形ABC面积是1/2×4×4=8.
∵AC⊥BC,∴AC⊥y轴,
∴点A的横坐标为3-4=-1,纵坐标为-2,
∴A点坐标为(-1,-2).
针对训练
下图中标明了李明家附近的一些地方,点A、B、C、D、E、F、G、H、I、J分别表示李明家、糖果店、书店、电影院、汽车站、街心花园、消防站、姥姥家、宠物店、邮局:
(1)写出书店和邮局的坐标;
C(100,300),
J(-300,-100).
考点4
用坐标表示地理位置
【例4】
(2)某星期日早晨,李明从家里出发,沿
(-100,200),(100,0),(200,100),(200,-200),
(-100,-200),(0,-100)的路线转了一下,又回到家里,写出他路上经过的地方.
经过的地方有糖果店→汽车站→电影院→消防站→宠物店→姥姥家.
连接他在(2)中经过的地点,你能得到什么图形?
针对训练
如图,请建立适当的平面直角坐标系,写出各地点的坐标.
解:如图,以学校A为原点,AB所在直线为x轴,垂直于x轴于点A的直线为y轴,表格中1小格代表1个单位长度.A(0,0),B(5,0),C(8,0),D(2,3),
E(-2,4),F(-7,0),G(-1,-2),H(3,-3).
当堂练习
当堂反馈
即学即用
1.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的
坐标是 .
2.点P(a-1,a2-9)在x轴负半轴上,则P点的坐标
是 .
(3
,-2)
(-4
,0)
当堂练习
3.点A(2,3)到x轴的距离为
;点B(-4,0)到y
轴的距离为
;点C到x轴的距离为1,到y轴的
距离为3,且在第三象限,则C点坐标是 .
3个单位
4个单位
(-3
,-1)
4.直角坐标系中,在y轴上有一点P
,且OP=5,则
P的坐标为
.
(0
,5)或(0
,-5)
5.已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是
.
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
6.
体操表演时,甲、乙、丙的位置如图所示,甲说:“我的位置用(-1,
1)表示.”那么乙、丙的位置该怎样表示呢?
解:由题意可得,可建立如图所示的平面直角坐标系.乙(-3,-1),丙(1,2).
THANKS!
平面直角坐标系
章末复习
目录页
讲授新课
当堂练习
课堂小结
新课导入
要点梳理
教学目标
教学重点
1.点与坐标一一对应.
点
坐标
确定
找到
要点梳理
要点梳理
2.象限、坐标符号、坐标轴上的点的坐标特点.
点的位置
横坐标符号
纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴
y轴
+
+
-
+
-
-
+
-
纵坐标为0
横坐标为0
要点梳理
要点梳理
3.平移规律:
要点梳理
要点梳理
4.用坐标表示地理位置:
(1)直角坐标系法
(2)方向角和距离法
考点精讲
典例精讲
归纳总结
考点精讲
考点精讲
考点1
平面直角坐标系与点的坐标
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的
距离为5,则点a的值是
.
【归纳拓展】
1.第一、三象限内点的横、纵坐标同号;
2.第二、四象限内点的横、纵坐标异号;
3.平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的
距离是它横坐标的绝对值;
4.平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线
上的点的横坐标相同.
-2
针对训练
1.已知点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是
______
_________.
2.已知点P在第二象限,且到x轴、y轴的距离分别为2和3,
则P点坐标为
.
或(6,-6)
(3,3)
(-3,2)
考点2
坐标与平移
【例2】如图,把三角形ABC经过一定的变换得到三角形A′B′C′,如果三角形ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为
.
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
(a+3,b+2)
将点(2,-5)向左平移1个单位长度,再向上平移6个单位长度得到点
.
针对训练
(1,1)
向左平移a个单位对应点P2(x-a,y)
总结归纳
向右平移a个单位对应点
P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
典例精析
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8)
B.(1,-2)
C.(-6,-1)
D.(0,-1)
点的平移变换:左右移动改变点的横坐标,左减右
加;上下移动改变点的纵坐标,下减上加.
归纳
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
考点3
平面作图及求坐标系中的几何图形面积
【例3】(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个
单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A(0,2)
B(4,3)
C(3,0)
S=3×4-1/2×2×3-1/2×1×4
-1/2×1×3=5.5
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:(一)通常用割或补的方法将要求图形转化为一些特殊的图形,去间接计算面积.
(二)需要将已知点的坐标转化为线段的长度,以满足求面积的需要.
已知直角三角形ABC的直角边BC=AC,
且B(3,2),C(3,-2),求点A的坐标及三
角形ABC的面积.
A
B
C
O
x
y
解:∵B(3,2),C(3,-2),
∴BC∥y轴,且BC=2-(-2)=4,
∴AC=BC=4.
∴三角形ABC面积是1/2×4×4=8.
∵AC⊥BC,∴AC⊥y轴,
∴点A的横坐标为3-4=-1,纵坐标为-2,
∴A点坐标为(-1,-2).
针对训练
下图中标明了李明家附近的一些地方,点A、B、C、D、E、F、G、H、I、J分别表示李明家、糖果店、书店、电影院、汽车站、街心花园、消防站、姥姥家、宠物店、邮局:
(1)写出书店和邮局的坐标;
C(100,300),
J(-300,-100).
考点4
用坐标表示地理位置
【例4】
(2)某星期日早晨,李明从家里出发,沿
(-100,200),(100,0),(200,100),(200,-200),
(-100,-200),(0,-100)的路线转了一下,又回到家里,写出他路上经过的地方.
经过的地方有糖果店→汽车站→电影院→消防站→宠物店→姥姥家.
连接他在(2)中经过的地点,你能得到什么图形?
针对训练
如图,请建立适当的平面直角坐标系,写出各地点的坐标.
解:如图,以学校A为原点,AB所在直线为x轴,垂直于x轴于点A的直线为y轴,表格中1小格代表1个单位长度.A(0,0),B(5,0),C(8,0),D(2,3),
E(-2,4),F(-7,0),G(-1,-2),H(3,-3).
当堂练习
当堂反馈
即学即用
1.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的
坐标是 .
2.点P(a-1,a2-9)在x轴负半轴上,则P点的坐标
是 .
(3
,-2)
(-4
,0)
当堂练习
3.点A(2,3)到x轴的距离为
;点B(-4,0)到y
轴的距离为
;点C到x轴的距离为1,到y轴的
距离为3,且在第三象限,则C点坐标是 .
3个单位
4个单位
(-3
,-1)
4.直角坐标系中,在y轴上有一点P
,且OP=5,则
P的坐标为
.
(0
,5)或(0
,-5)
5.已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是
.
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
6.
体操表演时,甲、乙、丙的位置如图所示,甲说:“我的位置用(-1,
1)表示.”那么乙、丙的位置该怎样表示呢?
解:由题意可得,可建立如图所示的平面直角坐标系.乙(-3,-1),丙(1,2).
THANKS!
