2020-2021学年八年级数学人教版下册第二十章《20.2.2 数据分析的应用类型》课件(共27张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第二十章《20.2.2 数据分析的应用类型》课件(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 989.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览






文档简介
第二十章
20.2.2 数据分析的应用类型
人教版数学八年级下册
1
类型
平均数、方差的应用
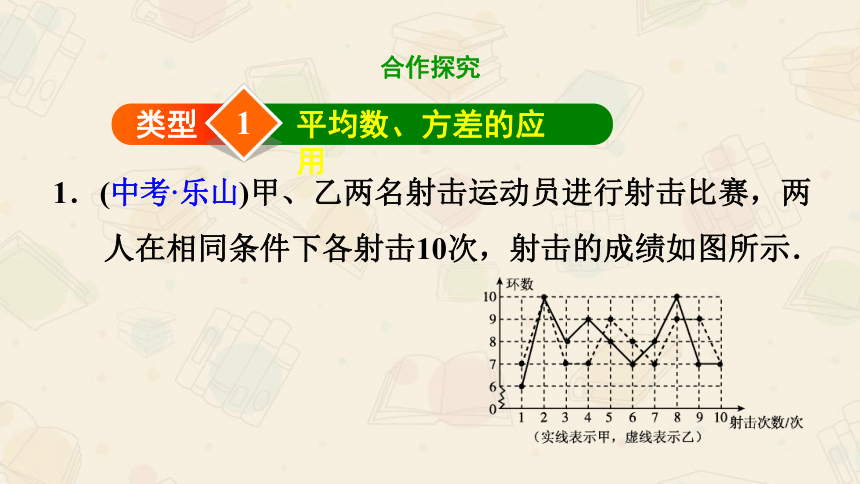
1.(中考·乐山)甲、乙两名射击运动员进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.
合作探究
根据图中信息,回答下列问题:
(1)甲的平均数是________,乙的中位数是________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪名运动员的射击成绩更稳定?
8环
7.5环
(2)s甲2= ×[(6-8)2+(10-8)2+…+(7-8)2]=1.6.
∵ = ×(7+10+…+7)=8(环),
∴s乙2= ×[(7-8)2+(10-8)2+…+(7-8)2]=1.2.
∵s乙2 <s甲2 ,
∴乙运动员的射击成绩更稳定.
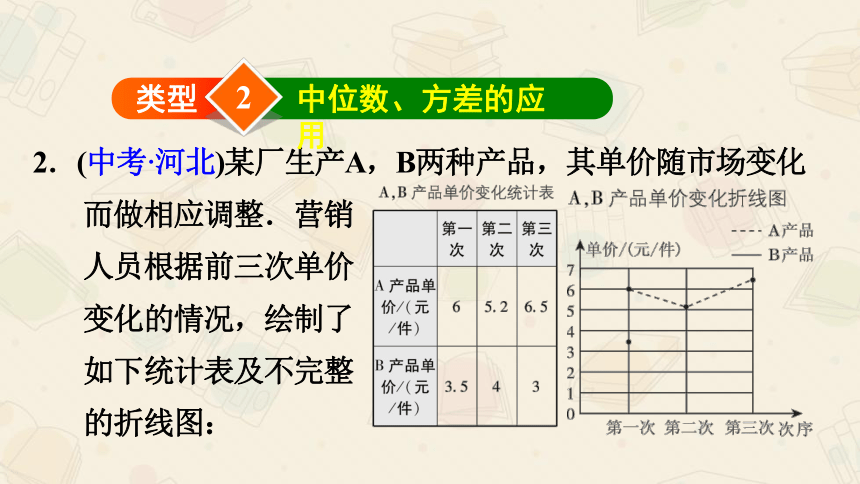
2.(中考·河北)某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销
人员根据前三次单价
变化的情况,绘制了
如下统计表及不完整
的折线图:
2
类型
中位数、方差的应用
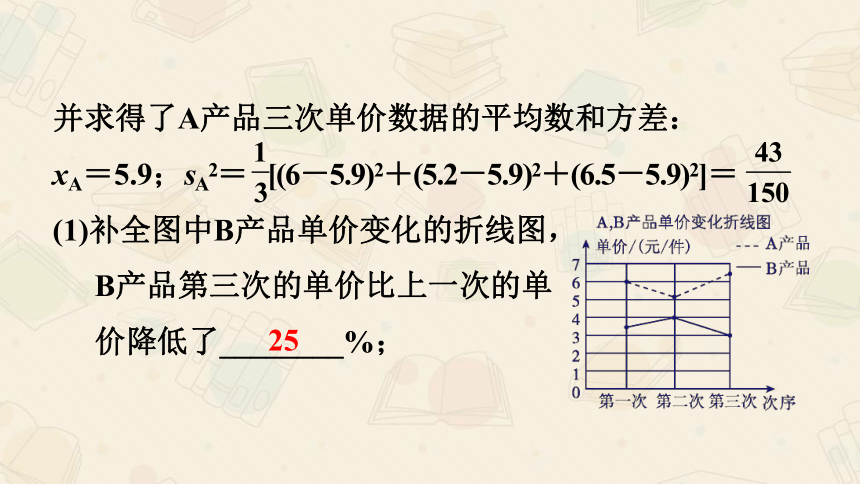
并求得了A产品三次单价数据的平均数和方差:
xA=5.9;sA2= [(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=
(1)补全图中B产品单价变化的折线图,
B产品第三次的单价比上一次的单
价降低了________%;
25
(2)求B产品三次单价数据的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
(2) ,
∵ < ,
∴B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价数据的中位数为 ;对于B产品,∵m>0,
∴第四次单价大于3元/件.
又∵ ×2-1= > ,
∴第四次单价小于4元/件.
∴
∴m=25.
3
类型
平均数、中位数、方差与统计图的应用
3.某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示.
(1)根据上图填写下表:
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
8.5
0.7
8
(2)从平均数看,两班平均数相同,则甲、乙两班的成绩一样好;
从中位数看,甲班的中位数大,所以甲班的成绩较好;
从众数看,乙班的众数大,所以乙班的成绩较好;
从方差看,甲班的方差小,所以甲班的成绩更稳定.
课后练习
173
2.9
25
二
一
再见
20.2.2 数据分析的应用类型
人教版数学八年级下册
1
类型
平均数、方差的应用
1.(中考·乐山)甲、乙两名射击运动员进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.
合作探究
根据图中信息,回答下列问题:
(1)甲的平均数是________,乙的中位数是________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪名运动员的射击成绩更稳定?
8环
7.5环
(2)s甲2= ×[(6-8)2+(10-8)2+…+(7-8)2]=1.6.
∵ = ×(7+10+…+7)=8(环),
∴s乙2= ×[(7-8)2+(10-8)2+…+(7-8)2]=1.2.
∵s乙2 <s甲2 ,
∴乙运动员的射击成绩更稳定.
2.(中考·河北)某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销
人员根据前三次单价
变化的情况,绘制了
如下统计表及不完整
的折线图:
2
类型
中位数、方差的应用
并求得了A产品三次单价数据的平均数和方差:
xA=5.9;sA2= [(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=
(1)补全图中B产品单价变化的折线图,
B产品第三次的单价比上一次的单
价降低了________%;
25
(2)求B产品三次单价数据的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
(2) ,
∵ < ,
∴B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价数据的中位数为 ;对于B产品,∵m>0,
∴第四次单价大于3元/件.
又∵ ×2-1= > ,
∴第四次单价小于4元/件.
∴
∴m=25.
3
类型
平均数、中位数、方差与统计图的应用
3.某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示.
(1)根据上图填写下表:
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
8.5
0.7
8
(2)从平均数看,两班平均数相同,则甲、乙两班的成绩一样好;
从中位数看,甲班的中位数大,所以甲班的成绩较好;
从众数看,乙班的众数大,所以乙班的成绩较好;
从方差看,甲班的方差小,所以甲班的成绩更稳定.
课后练习
173
2.9
25
二
一
再见
