2020-2021学年 人教版八年级数学下册第18章 平行四边形 常考题专题训练(二)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年 人教版八年级数学下册第18章 平行四边形 常考题专题训练(二)(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 229.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览



文档简介
八年级数学人教版下册第18章《平行四边形》
经典常考题专题训练(二)
1.在正方形ABCD中,E是△ABD内的点,EB=EC.
(1)如图1,若EB=BC,求∠EBD的度数;
(2)如图2,EC与BD交于点F,连接AE,若S四边形ABFE=a,试探究线段FC与BE之间的数量关系,并说明理由.
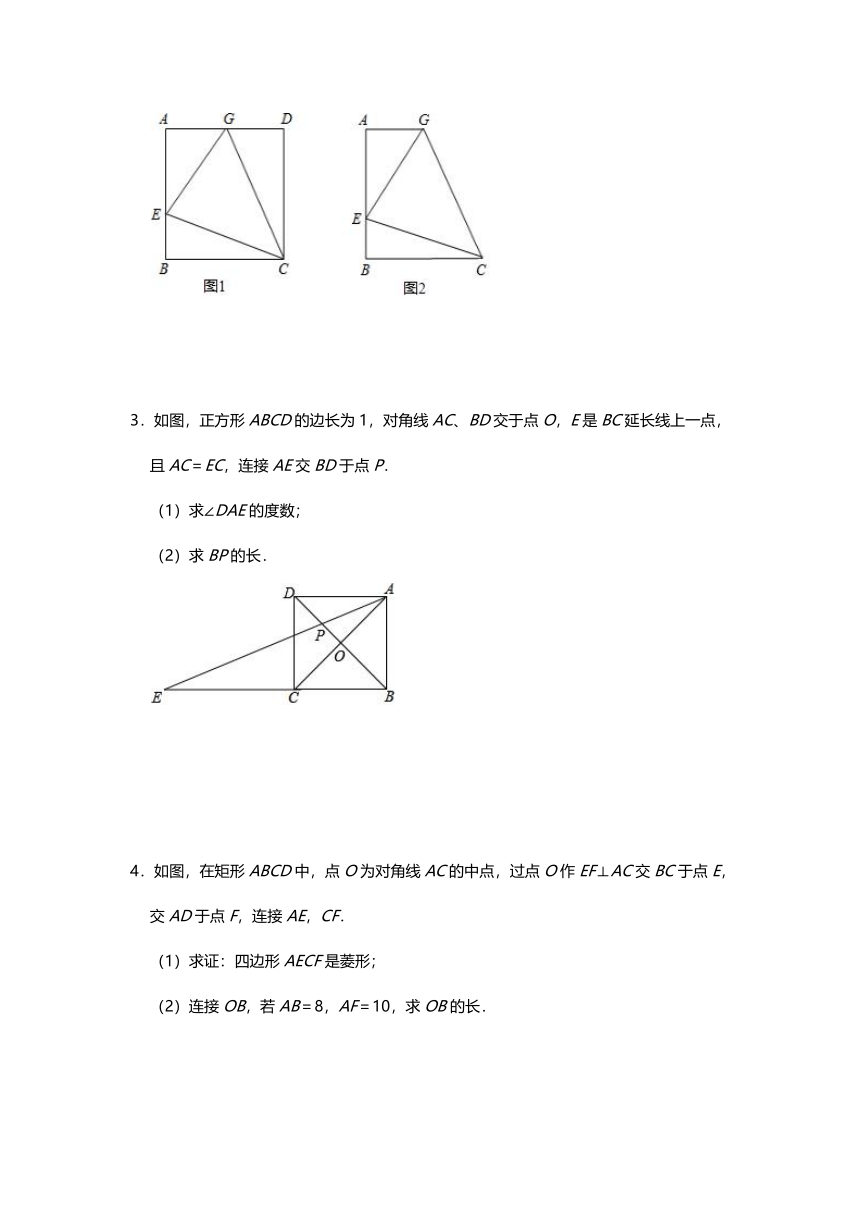
2.(1)如图1,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,那么EG与图中两条线段的和相等?证明你的结论.
(2)请用(1)中所积累的经验和知识完成此题,如图2,在四边形ABCD中,AG∥BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
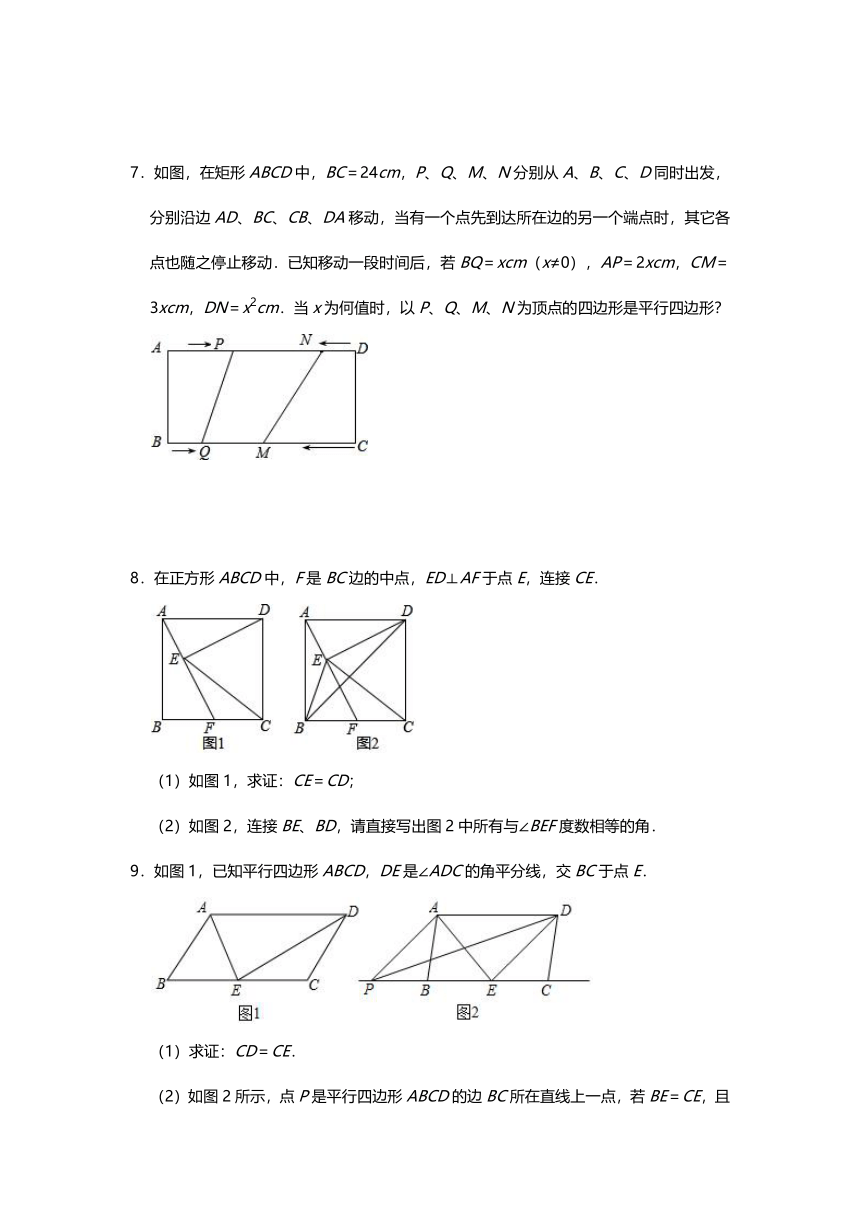
3.如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
(1)求∠DAE的度数;
(2)求BP的长.
4.如图,在矩形ABCD中,点O为对角线AC的中点,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)连接OB,若AB=8,AF=10,求OB的长.
5.如图,在平行四边形ABCD中,对角线AC,BD交于点O,E是AD上任意一点,连接EO并延长,交BC于点F,连接AF,CE.
(1)求证:四边形AFCE是平行四边形;
(2)若∠DAC=60°,∠ADB=15°,AC=6.求出平行四边形ABCD的边BC上的高h的值.
6.如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.
(1)求证:△AOH≌△BOE;
(2)求∠AGO的度数;
(3)若∠OGC=90°,BG=,求△OGC的面积.
7.如图,在矩形ABCD中,BC=24cm,P、Q、M、N分别从A、B、C、D同时出发,分别沿边AD、BC、CB、DA移动,当有一个点先到达所在边的另一个端点时,其它各点也随之停止移动.已知移动一段时间后,若BQ=xcm(x≠0),AP=2xcm,CM=3xcm,DN=x2cm.当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形?
8.在正方形ABCD中,F是BC边的中点,ED⊥AF于点E,连接CE.
(1)如图1,求证:CE=CD;
(2)如图2,连接BE、BD,请直接写出图2中所有与∠BEF度数相等的角.
9.如图1,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE.
(2)如图2所示,点P是平行四边形ABCD的边BC所在直线上一点,若BE=CE,且AE=3,DE=4,求△APD的面积.
10.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
11.如图,已知平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点M、N.
(1)求证:四边形CMAN是平行四边形
(2)已知DE=8,FN=6,求BN的长.
12.如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形.
(2)求BC的长.
13.如图,长方形ABCD中,AB∥CD,∠D=90°,AB=CD,AD=4cm,点P从点D出发(不含点D)以2cm/s的速度沿D→A→B的方向运动到点B停止,点P出发1s后,点Q才开始从点C出发以acm/s的速度沿C→D的方向运动到点D停止,当点P到达点B时,点Q恰好到达点D.
(1)当点P到达点A时,△CPQ的面积为3cm2,求CD的长;
(2)在(1)的条件下,设点P运动时间为t(s),运动过程中△BPQ的面积为S(cm2),请用含t(s)的式子表示面积S(cm2),并直接写出t的取值范围.
14.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若AC=6,AB=8,求菱形ADCF的面积.
15.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.
(1)若∠B=30°,AC=6,求CE的长;
(2)过点F作AB的垂线,垂足为G,连接EG,试判断四边形CEGF的形状,并说明原因.
参考答案
1.解:(1)如图1,∵EB=BC=EC,
∴△EBC是等边三角形,
∴∠EBC=60°,
∵四边形ABCD是正方形,
∴∠CBD=45°,
∴∠EBD=∠EBC﹣∠CBD=60°﹣45°=15°;
(2)线段FC与BE之间的等量关系是:FC?BE=2a,理由是:
如图2,连接AF交BE于G,
∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠DBC,
∵BF=BF,
∴△ABF≌△CBF(SAS),
∴AF=CF,∠BAF=∠BCF,
∵EB=EC,
∴∠ECB=∠EBC,
∵∠ABC=∠DCB=90°,
∴∠ABE=∠DCE,
∴∠ABE+∠BAF=∠DCE+∠BCE=90°,
∴∠AGB=90°,
∴AF⊥BE,
∴S四边形ABFE=S△ABE+S△BEF,
=,
=,
=,
∵S四边形ABFE=a,
∴=a,
∴FC?BE=2a.
2.解:(1)EG=BE+DG.
如图1,延长AD至F,使DF=BE,连接CF,
∵四边形ABCD为正方形,
∴BC=DC,∠ABC=∠ADC=∠BCD=90°,
∵∠CDF=180﹣∠ADC,
∴∠CDF=90°,
∴∠ABC=∠CDF,
∵BE=DF,
∴△EBC≌△FDC(SAS),
∴∠BCE=∠DCF,EC=FC,
∵∠ECG=45°,
∴∠BCE+∠GCD=∠BCD﹣∠ECG=90°﹣45°=45°,
∴∠GCD+DCF=∠FCG=45°,
∴∠ECG=∠FCG,
∵GC=GC,
∴△ECG≌△FCG(SAS),
∴EG=GF,
∵GF=GD+DF=GD+BE,
∴EG=GD+BE.
(2)如图2,过点C作CD⊥AG,交AG的延长线于D.
∵AG∥BC,
∴∠A+∠B=180°,
∵∠B=90°,
∴∠A=180°﹣∠B=90°,
∵∠CDA=90°,AB=BC,
∴四边形ABCD是正方形,
∵AB=BC=12,
∴CD=AD=12,
∵BE=4,
∴AE=AB﹣BE=8,
设EG=x,由(1)知EG=BE+GD,
∴GD=x﹣4,
∴AG=AD﹣GD=12﹣(x﹣4)=16﹣x,
在Rt△AEG中:GE2=AG2+AE2,
∴x2=(16﹣x)2+82,解得x=10,
∴EG=10.
3.解:(1)∵四边形ABCD的正方形,
∴∠ACB=45°,AD∥BC,
∵AC=EC,
∴∠E=∠EAC,
∵∠ACB=∠E+∠EAC=45°,
∴∠E=22.5°,
∵AD∥BC,
∴∠DAE=∠E=22.5°;
(2)∵四边形ABCD是正方形,正方形ABCD的边长是1,
∴AB=1,∠DAB=90°,∠DBC=45°,
∵∠DAE=22.5°,
∴∠BAP=90°﹣22.5°=67.5°,∠APB=∠E+∠DBC=22.5°+45°=67.5°,
∴∠BAP=∠APB,
∴BP=AB=1.
4.证明:(1)∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)如图,
∵AB=8,AF=AE=EC=10,
∴BE===6,
∴BC=16,
∴AC===8,
∵AO=CO,∠ABC=90°,
∴BO=AC=4.
5.证明:(1)∵四边形ABCD是平行四边形
∴AD∥BC,AO=CO
∴∠AEF=∠CFE,∠EAC=∠FCA,且AO=CO
∴△AOE≌△COF(AAS)
∴OF=OE,且AO=CO
∴四边形AFCE是平行四边形;
(2)∵∠DAC=60°
∴,
∴h=×AC=3.
6.(1)证明:∵四边形ABCD是正方形,
∴OA=OB,∠ABC=90°,AC⊥BD,
∴∠AOB=∠BOE=90°,
∵AF⊥BE,
∴∠GAE+∠AEG=∠OBE+∠AEG=90°,
∴∠GAE=∠OBE,
在△AOH和△BOE中,,
∴△AOH≌△BOE(ASA);
(2)∠AGO=45°;
(3)S△OGC=OG?CG=×6=3.
7.当x为2或﹣3+时,以P、Q、M、N为顶点的四边形是平行四边形.
8.(1)证明:作CH⊥DE交DE于点H,交AD于点N,
∵ED⊥AF,CH⊥DE,
∴AF∥CN,又AN∥CF,
∴四边形AFCN为平行四边形,
∴AN=CF,
∵F是BC边的中点,AD=BC,
∴N是AD边的中点,
∵NH∥AE,DN=NA,
∴DH=HE,又CH⊥DE,
∴CE=CD;
(2)解:作BG⊥AF于点G,
设正方形的边长为4a,则BF=2a,
由勾股定理得,AF===2a,
×AB×BF=×AF×BG,即×4a×2a=×2a×BG,
解得,BG=a,
∵∠ABF=90°,BG⊥AF,
∴BF2=FG?FA,即(2a)2=FG?2a,
解得,FG=a,
∵∠BAF+∠DAE=90°,∠ADE+∠DAE=90°,
∴∠BAG=∠ADE,
在△BAG和△ADE中,
∴△BAG≌△ADE(AAS)
∴AE=BG=a,
∴EG=AF﹣AE﹣FG=a,
∴BG=EG,
∴∠BEF=45°,
则图2中所有与∠BEF度数相等的角有∠ABD、∠CBD、∠ADB、∠CDB.
9.(1)证明:∵DE是∠ADC的角平分线,
∴∠ADE=∠CDE,
在平行四边形ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CD=CE;
(2)解:∵CD=CE,BE=CE,
∴BE=CD=AB,
∴△ABE为等腰三角形,
∴设∠BAE=∠BEA=α,∠CED=∠CDE=β,
∴∠ABE=180°﹣2α,∠DCE=180°﹣2β,
又∵∠ABE+∠DCE=180°,
∴180°﹣2α+180°﹣2β=180°,
∴α+β=90°,
∴∠AED=90°,
即△AED为直角三角形,
∴AD===5,
过点E作EK⊥AD,
∴EK==,
△APD的面积=AD?EK=×5×=6.
10.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)方法一:如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DM=BD=.
方法二:过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FH=CF=3,
∴MH=CE=3,
∴DH=11,
∴DM==.
11.(1)证明:∵AE⊥BD,CF⊥BD,
∴AM∥CN,
∵四边形ABCD是平行四边形,
∴CM∥AN
∴四边形CMAN是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE与△CBF中,∠ADE=∠CBF,∠AED=∠CFB,AD=BC,
∴△ADE≌△CBF(AAS);
∴DE=BF=8,
∵FN=6,
∴.
12.解:(1)证明:∵∠ACB=90°,DE⊥BC,
∴AC∥DE
又∵CE∥AD
∴四边形ACED是平行四边形.
(2)∵四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD===2.
∵D是BC的中点,
∴BC=2CD=4.
13.解:(1)设点P运动时间为t(s),根据题意,得
点P出发1s后,点Q才开始从点C出发以acm/s的速度沿C→D的方向运动到点D停止,
当点P到达点B时,点Q恰好到达点D.
∴2(t﹣2)=a(t﹣1),
当点P到达点A时,△CPQ的面积为3cm2,
即a×1×4=3,
∴a=.
即2(t﹣2)=(t﹣1),
解得t=5,
所以CD=a(t﹣1)=6.
答:CD的长为6;
(2)根据题意,得
BC=AD=4,CD=6
DP=2t,CQ=1.5(t﹣1),
①点P的运动时间为t,0﹣1秒时点Q还在点C,
△BPQ面积不变为=12;
即S=12(0<t≤1)
②当1<t≤2时,
DQ=6﹣1.5(t﹣1)=7.5﹣1.5t,
S=S梯形DPBC﹣S△DPQ﹣S△BQC
=(2t+4)×6﹣×2t×(7.5﹣1.5t)﹣×1.5(t﹣1)×4
=1.5t2﹣4.5t+15;
③当2<t≤5时,
BP=10﹣2t,
S=BP?BC
=(10﹣2t)×4
=20﹣4t.
综上所述:
运动过程中△BPQ的面积为S(cm2),
用含t(s)的式子表示面积S(cm2)为:
S=12
(0<t≤1)
或S=1.5t2﹣4.5t+15(1<t≤2)
或S=20﹣4t(2<t≤5).
14.解:(1)证明:
∵E是AD的中点
∴AE=DE
∵AF∥BC
∴∠AFE=∠DBE
在△AEF和△DEB中
∴△AEF≌△DEB(AAS)
∴AF=DB
∴四边形ADCF是平行四边形
∵∠BAC=90°,
D是BC的中点
∴AD=CD=BC
∴四边形ADCF是菱形;
(2)解:法一、
设AF到CD的距离为h,
∵AF∥BC,
AF=BD=CD,
∠BAC=90°,
∴S菱形ADCF=CD?h
=BC?h
=S△ABC
=AB?AC
=.
法二、
连接DF
∵AF=DB,
AF∥DB
∴四边形ABDF是平行四边形
∴DF=AB=8
∴S菱形ADCF=AC?DF
=.
法三、
∵三角形ABD与三角形ADC与三角形AFC的面积相等,
∴菱形ADCF的面积等于三角形ABC的面积为24.
答:菱形ADCF的面积为24.
15.解:(1)∵∠ACB=90°,∠B=30°,
∴∠CAB=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
∵AF平分∠CAB,
∴∠CAF=∠BAF=30°,
∴CE=AE,
过点E用EH垂直于AC于点H,
∴CH=AH
∵AC=6,
∴CE=2
答:CE的长为2;
(2)∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=GF,
在Rt△ACF与Rt△AGF中,
AF=AF,CF=GF,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG,
∵CD⊥AB,FG⊥AB,
∴CD∥FG,
∴∠CEF=∠EFG,
∴∠CEF=∠CFE,
∴CE=CF,
∴CE=FG,
∴四边形CEGF是菱形
经典常考题专题训练(二)
1.在正方形ABCD中,E是△ABD内的点,EB=EC.
(1)如图1,若EB=BC,求∠EBD的度数;
(2)如图2,EC与BD交于点F,连接AE,若S四边形ABFE=a,试探究线段FC与BE之间的数量关系,并说明理由.
2.(1)如图1,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,那么EG与图中两条线段的和相等?证明你的结论.
(2)请用(1)中所积累的经验和知识完成此题,如图2,在四边形ABCD中,AG∥BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
3.如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
(1)求∠DAE的度数;
(2)求BP的长.
4.如图,在矩形ABCD中,点O为对角线AC的中点,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)连接OB,若AB=8,AF=10,求OB的长.
5.如图,在平行四边形ABCD中,对角线AC,BD交于点O,E是AD上任意一点,连接EO并延长,交BC于点F,连接AF,CE.
(1)求证:四边形AFCE是平行四边形;
(2)若∠DAC=60°,∠ADB=15°,AC=6.求出平行四边形ABCD的边BC上的高h的值.
6.如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.
(1)求证:△AOH≌△BOE;
(2)求∠AGO的度数;
(3)若∠OGC=90°,BG=,求△OGC的面积.
7.如图,在矩形ABCD中,BC=24cm,P、Q、M、N分别从A、B、C、D同时出发,分别沿边AD、BC、CB、DA移动,当有一个点先到达所在边的另一个端点时,其它各点也随之停止移动.已知移动一段时间后,若BQ=xcm(x≠0),AP=2xcm,CM=3xcm,DN=x2cm.当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形?
8.在正方形ABCD中,F是BC边的中点,ED⊥AF于点E,连接CE.
(1)如图1,求证:CE=CD;
(2)如图2,连接BE、BD,请直接写出图2中所有与∠BEF度数相等的角.
9.如图1,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE.
(2)如图2所示,点P是平行四边形ABCD的边BC所在直线上一点,若BE=CE,且AE=3,DE=4,求△APD的面积.
10.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
11.如图,已知平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点M、N.
(1)求证:四边形CMAN是平行四边形
(2)已知DE=8,FN=6,求BN的长.
12.如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形.
(2)求BC的长.
13.如图,长方形ABCD中,AB∥CD,∠D=90°,AB=CD,AD=4cm,点P从点D出发(不含点D)以2cm/s的速度沿D→A→B的方向运动到点B停止,点P出发1s后,点Q才开始从点C出发以acm/s的速度沿C→D的方向运动到点D停止,当点P到达点B时,点Q恰好到达点D.
(1)当点P到达点A时,△CPQ的面积为3cm2,求CD的长;
(2)在(1)的条件下,设点P运动时间为t(s),运动过程中△BPQ的面积为S(cm2),请用含t(s)的式子表示面积S(cm2),并直接写出t的取值范围.
14.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若AC=6,AB=8,求菱形ADCF的面积.
15.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.
(1)若∠B=30°,AC=6,求CE的长;
(2)过点F作AB的垂线,垂足为G,连接EG,试判断四边形CEGF的形状,并说明原因.
参考答案
1.解:(1)如图1,∵EB=BC=EC,
∴△EBC是等边三角形,
∴∠EBC=60°,
∵四边形ABCD是正方形,
∴∠CBD=45°,
∴∠EBD=∠EBC﹣∠CBD=60°﹣45°=15°;
(2)线段FC与BE之间的等量关系是:FC?BE=2a,理由是:
如图2,连接AF交BE于G,
∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠DBC,
∵BF=BF,
∴△ABF≌△CBF(SAS),
∴AF=CF,∠BAF=∠BCF,
∵EB=EC,
∴∠ECB=∠EBC,
∵∠ABC=∠DCB=90°,
∴∠ABE=∠DCE,
∴∠ABE+∠BAF=∠DCE+∠BCE=90°,
∴∠AGB=90°,
∴AF⊥BE,
∴S四边形ABFE=S△ABE+S△BEF,
=,
=,
=,
∵S四边形ABFE=a,
∴=a,
∴FC?BE=2a.
2.解:(1)EG=BE+DG.
如图1,延长AD至F,使DF=BE,连接CF,
∵四边形ABCD为正方形,
∴BC=DC,∠ABC=∠ADC=∠BCD=90°,
∵∠CDF=180﹣∠ADC,
∴∠CDF=90°,
∴∠ABC=∠CDF,
∵BE=DF,
∴△EBC≌△FDC(SAS),
∴∠BCE=∠DCF,EC=FC,
∵∠ECG=45°,
∴∠BCE+∠GCD=∠BCD﹣∠ECG=90°﹣45°=45°,
∴∠GCD+DCF=∠FCG=45°,
∴∠ECG=∠FCG,
∵GC=GC,
∴△ECG≌△FCG(SAS),
∴EG=GF,
∵GF=GD+DF=GD+BE,
∴EG=GD+BE.
(2)如图2,过点C作CD⊥AG,交AG的延长线于D.
∵AG∥BC,
∴∠A+∠B=180°,
∵∠B=90°,
∴∠A=180°﹣∠B=90°,
∵∠CDA=90°,AB=BC,
∴四边形ABCD是正方形,
∵AB=BC=12,
∴CD=AD=12,
∵BE=4,
∴AE=AB﹣BE=8,
设EG=x,由(1)知EG=BE+GD,
∴GD=x﹣4,
∴AG=AD﹣GD=12﹣(x﹣4)=16﹣x,
在Rt△AEG中:GE2=AG2+AE2,
∴x2=(16﹣x)2+82,解得x=10,
∴EG=10.
3.解:(1)∵四边形ABCD的正方形,
∴∠ACB=45°,AD∥BC,
∵AC=EC,
∴∠E=∠EAC,
∵∠ACB=∠E+∠EAC=45°,
∴∠E=22.5°,
∵AD∥BC,
∴∠DAE=∠E=22.5°;
(2)∵四边形ABCD是正方形,正方形ABCD的边长是1,
∴AB=1,∠DAB=90°,∠DBC=45°,
∵∠DAE=22.5°,
∴∠BAP=90°﹣22.5°=67.5°,∠APB=∠E+∠DBC=22.5°+45°=67.5°,
∴∠BAP=∠APB,
∴BP=AB=1.
4.证明:(1)∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)如图,
∵AB=8,AF=AE=EC=10,
∴BE===6,
∴BC=16,
∴AC===8,
∵AO=CO,∠ABC=90°,
∴BO=AC=4.
5.证明:(1)∵四边形ABCD是平行四边形
∴AD∥BC,AO=CO
∴∠AEF=∠CFE,∠EAC=∠FCA,且AO=CO
∴△AOE≌△COF(AAS)
∴OF=OE,且AO=CO
∴四边形AFCE是平行四边形;
(2)∵∠DAC=60°
∴,
∴h=×AC=3.
6.(1)证明:∵四边形ABCD是正方形,
∴OA=OB,∠ABC=90°,AC⊥BD,
∴∠AOB=∠BOE=90°,
∵AF⊥BE,
∴∠GAE+∠AEG=∠OBE+∠AEG=90°,
∴∠GAE=∠OBE,
在△AOH和△BOE中,,
∴△AOH≌△BOE(ASA);
(2)∠AGO=45°;
(3)S△OGC=OG?CG=×6=3.
7.当x为2或﹣3+时,以P、Q、M、N为顶点的四边形是平行四边形.
8.(1)证明:作CH⊥DE交DE于点H,交AD于点N,
∵ED⊥AF,CH⊥DE,
∴AF∥CN,又AN∥CF,
∴四边形AFCN为平行四边形,
∴AN=CF,
∵F是BC边的中点,AD=BC,
∴N是AD边的中点,
∵NH∥AE,DN=NA,
∴DH=HE,又CH⊥DE,
∴CE=CD;
(2)解:作BG⊥AF于点G,
设正方形的边长为4a,则BF=2a,
由勾股定理得,AF===2a,
×AB×BF=×AF×BG,即×4a×2a=×2a×BG,
解得,BG=a,
∵∠ABF=90°,BG⊥AF,
∴BF2=FG?FA,即(2a)2=FG?2a,
解得,FG=a,
∵∠BAF+∠DAE=90°,∠ADE+∠DAE=90°,
∴∠BAG=∠ADE,
在△BAG和△ADE中,
∴△BAG≌△ADE(AAS)
∴AE=BG=a,
∴EG=AF﹣AE﹣FG=a,
∴BG=EG,
∴∠BEF=45°,
则图2中所有与∠BEF度数相等的角有∠ABD、∠CBD、∠ADB、∠CDB.
9.(1)证明:∵DE是∠ADC的角平分线,
∴∠ADE=∠CDE,
在平行四边形ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CD=CE;
(2)解:∵CD=CE,BE=CE,
∴BE=CD=AB,
∴△ABE为等腰三角形,
∴设∠BAE=∠BEA=α,∠CED=∠CDE=β,
∴∠ABE=180°﹣2α,∠DCE=180°﹣2β,
又∵∠ABE+∠DCE=180°,
∴180°﹣2α+180°﹣2β=180°,
∴α+β=90°,
∴∠AED=90°,
即△AED为直角三角形,
∴AD===5,
过点E作EK⊥AD,
∴EK==,
△APD的面积=AD?EK=×5×=6.
10.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)方法一:如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DM=BD=.
方法二:过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FH=CF=3,
∴MH=CE=3,
∴DH=11,
∴DM==.
11.(1)证明:∵AE⊥BD,CF⊥BD,
∴AM∥CN,
∵四边形ABCD是平行四边形,
∴CM∥AN
∴四边形CMAN是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE与△CBF中,∠ADE=∠CBF,∠AED=∠CFB,AD=BC,
∴△ADE≌△CBF(AAS);
∴DE=BF=8,
∵FN=6,
∴.
12.解:(1)证明:∵∠ACB=90°,DE⊥BC,
∴AC∥DE
又∵CE∥AD
∴四边形ACED是平行四边形.
(2)∵四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD===2.
∵D是BC的中点,
∴BC=2CD=4.
13.解:(1)设点P运动时间为t(s),根据题意,得
点P出发1s后,点Q才开始从点C出发以acm/s的速度沿C→D的方向运动到点D停止,
当点P到达点B时,点Q恰好到达点D.
∴2(t﹣2)=a(t﹣1),
当点P到达点A时,△CPQ的面积为3cm2,
即a×1×4=3,
∴a=.
即2(t﹣2)=(t﹣1),
解得t=5,
所以CD=a(t﹣1)=6.
答:CD的长为6;
(2)根据题意,得
BC=AD=4,CD=6
DP=2t,CQ=1.5(t﹣1),
①点P的运动时间为t,0﹣1秒时点Q还在点C,
△BPQ面积不变为=12;
即S=12(0<t≤1)
②当1<t≤2时,
DQ=6﹣1.5(t﹣1)=7.5﹣1.5t,
S=S梯形DPBC﹣S△DPQ﹣S△BQC
=(2t+4)×6﹣×2t×(7.5﹣1.5t)﹣×1.5(t﹣1)×4
=1.5t2﹣4.5t+15;
③当2<t≤5时,
BP=10﹣2t,
S=BP?BC
=(10﹣2t)×4
=20﹣4t.
综上所述:
运动过程中△BPQ的面积为S(cm2),
用含t(s)的式子表示面积S(cm2)为:
S=12
(0<t≤1)
或S=1.5t2﹣4.5t+15(1<t≤2)
或S=20﹣4t(2<t≤5).
14.解:(1)证明:
∵E是AD的中点
∴AE=DE
∵AF∥BC
∴∠AFE=∠DBE
在△AEF和△DEB中
∴△AEF≌△DEB(AAS)
∴AF=DB
∴四边形ADCF是平行四边形
∵∠BAC=90°,
D是BC的中点
∴AD=CD=BC
∴四边形ADCF是菱形;
(2)解:法一、
设AF到CD的距离为h,
∵AF∥BC,
AF=BD=CD,
∠BAC=90°,
∴S菱形ADCF=CD?h
=BC?h
=S△ABC
=AB?AC
=.
法二、
连接DF
∵AF=DB,
AF∥DB
∴四边形ABDF是平行四边形
∴DF=AB=8
∴S菱形ADCF=AC?DF
=.
法三、
∵三角形ABD与三角形ADC与三角形AFC的面积相等,
∴菱形ADCF的面积等于三角形ABC的面积为24.
答:菱形ADCF的面积为24.
15.解:(1)∵∠ACB=90°,∠B=30°,
∴∠CAB=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
∵AF平分∠CAB,
∴∠CAF=∠BAF=30°,
∴CE=AE,
过点E用EH垂直于AC于点H,
∴CH=AH
∵AC=6,
∴CE=2
答:CE的长为2;
(2)∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=GF,
在Rt△ACF与Rt△AGF中,
AF=AF,CF=GF,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG,
∵CD⊥AB,FG⊥AB,
∴CD∥FG,
∴∠CEF=∠EFG,
∴∠CEF=∠CFE,
∴CE=CF,
∴CE=FG,
∴四边形CEGF是菱形
