2020-2021学年八年级数学北师大版下册第六章6.4.1多边形的内角和与外角和(一) 同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册第六章6.4.1多边形的内角和与外角和(一) 同步练习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 103.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 16:22:41 | ||
图片预览

文档简介
2020-2021学年北师大版八年级数学下册第六章6.4.1多边形的内角和与外角和(一)
同步练习题
A组(基础题)
一、填空题
1.(1)从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是_____;
(2)一个十二边形的内角和等于_____.
2.(1)从多边形的一个顶点可以画出4条对角线,则该多边形的内角和为_____;
(2)一个多边形的内角和比三角形内角和的2倍多180°,这个多边形的边数是_____.
3.从正n边形的一个顶点可以画5条对角线,则这个n边形的每个内角的度数为_____度.
4.(1)若一个正n边形的每个内角为108°,则这个正n边形的所有对角线的条数是5;
(2)从n边形一个顶点出发共有8条对角线,则这些对角线把原多边形分成_____个三角形.
二、选择题
5.多边形的内角和不可能为(
)
A.180°
B.540°
C.1
080°
D.1
200°
6.如果从多边形的一个顶点可以画出a条对角线,那么这a条对角线把该多边形分成的三角形的个数为(
)
A.a
B.a-3
C.a-2
D.a+1
7.(n+2)边形的内角和比n边形的内角和大(
)
A.180°
B.360°
C.n·180°
D.n·360°
8.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的内角和为(
)
A.540°
B.720°
C.900°
D.1
260°
三、解答题
9.(1)一个多边形的内角和比四边形的内角和多360°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
(2)已知一个多边形的内角和与外角和相加为1
800°,求这个多边形的对角线的条数.
10.若一个多边形的内角和是它的外角和的5倍,求这个多边形的边数和对角线的条数.
B组(中档题)
一、填空题
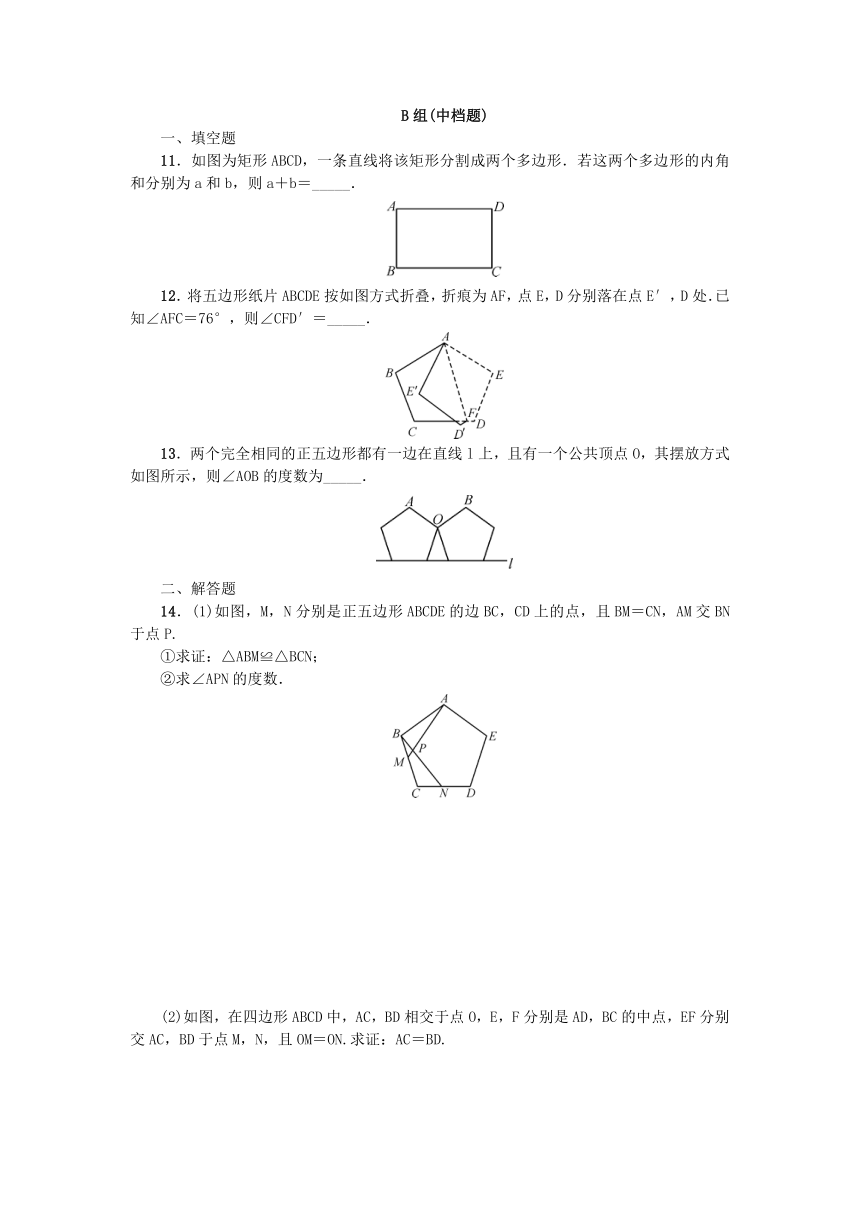
11.如图为矩形ABCD,一条直线将该矩形分割成两个多边形.若这两个多边形的内角和分别为a和b,则a+b=_____.
12.将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在点E′,D处.已知∠AFC=76°,则∠CFD′=_____.
13.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB的度数为_____.
二、解答题
14.(1)如图,M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
①求证:△ABM≌△BCN;
②求∠APN的度数.
(2)如图,在四边形ABCD中,AC,BD相交于点O,E,F分别是AD,BC的中点,EF分别交AC,BD于点M,N,且OM=ON.求证:AC=BD.
C组(综合题)
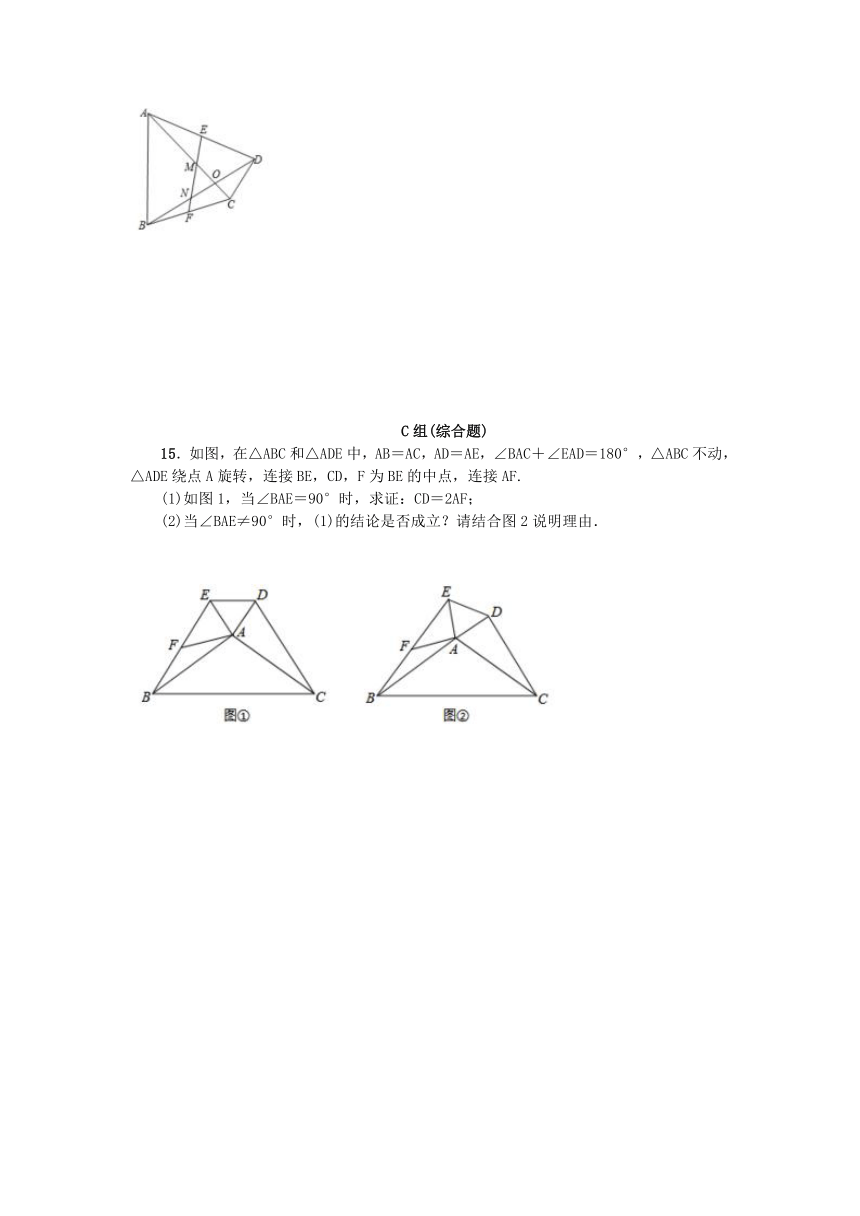
15.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图1,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图2说明理由.
参考答案
2020-2021学年北师大版八年级数学下册第六章6.4.1多边形的内角和与外角和(一)
同步练习题
A组(基础题)
一、填空题
1.(1)从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是8;
(2)一个十二边形的内角和等于1_800°.
2.(1)从多边形的一个顶点可以画出4条对角线,则该多边形的内角和为900°;
(2)一个多边形的内角和比三角形内角和的2倍多180°,这个多边形的边数是5.
3.从正n边形的一个顶点可以画5条对角线,则这个n边形的每个内角的度数为135度.
4.(1)若一个正n边形的每个内角为108°,则这个正n边形的所有对角线的条数是5;
(2)从n边形一个顶点出发共有8条对角线,则这些对角线把原多边形分成9个三角形.
二、选择题
5.多边形的内角和不可能为(D)
A.180°
B.540°
C.1
080°
D.1
200°
6.如果从多边形的一个顶点可以画出a条对角线,那么这a条对角线把该多边形分成的三角形的个数为(D)
A.a
B.a-3
C.a-2
D.a+1
7.(n+2)边形的内角和比n边形的内角和大(B)
A.180°
B.360°
C.n·180°
D.n·360°
8.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的内角和为(C)
A.540°
B.720°
C.900°
D.1
260°
三、解答题
9.(1)一个多边形的内角和比四边形的内角和多360°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形的边数为n,则
(n-2)·180°=360°+360°,解得n=6.
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为(360+360)÷6=120.
故这个多边形的每个内角是120°.
(2)已知一个多边形的内角和与外角和相加为1
800°,求这个多边形的对角线的条数.
解:设这个多边形是n边形,则(n-2)×180°=1
800°-360°,
解得n=10.
∴这个多边形的对角线的条数为10×(10-3)÷2=35(条).
10.若一个多边形的内角和是它的外角和的5倍,求这个多边形的边数和对角线的条数.
解:设这个多边形的边数为n,依题意,得
(n-2)·180°=5×360°,解得n=12.
则对角线的条数为=54(条).
∴这个多边形的边数是12,对角线的条数为54.
B组(中档题)
一、填空题
11.如图为矩形ABCD,一条直线将该矩形分割成两个多边形.若这两个多边形的内角和分别为a和b,则a+b=360°或540°或720°.
12.将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在点E′,D处.已知∠AFC=76°,则∠CFD′=28°.
13.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB的度数为108°.
二、解答题
14.(1)如图,M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
①求证:△ABM≌△BCN;
②求∠APN的度数.
解:①证明:∵ABCDE是正五边形,
∴AB=BC,∠ABM=∠C.
在△ABM和△BCN中,
∴△ABM≌△BCN(SAS).
②∵△ABM≌△BCN,
∴∠BAM=∠CBN.
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°.
∴∠APN=108°.
(2)如图,在四边形ABCD中,AC,BD相交于点O,E,F分别是AD,BC的中点,EF分别交AC,BD于点M,N,且OM=ON.求证:AC=BD.
证明:取AB和CD的中点G和H,连接EG,GF,FH,EH,则EH∥AC,EH=AC,HF∥BD,FH=BD,GE∥BD,
∴∠3=∠2,∠1=∠4.
∵OM=ON,
∴∠1=∠2.
∴∠4=∠3=∠1=∠2.
同理:∠EFH=∠GFE=∠1=∠2.
∴∠4=∠EFH.
∴EH=HF.
∵EH=AC,FH=BD,
∴AC=BD.
C组(综合题)
15.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图1,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图2说明理由.
解:(1)证明:∵∠BAC+∠EAD=180°,∠BAE=90°,
∴∠DAC=90°.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
∴BE=CD.
∵在Rt△ABE中,F为BE的中点,
∴BE=2AF.
∴CD=2AF.
(2)成立.
证明:延长EA交BC于点G,在AG上截取AH=AD.
∵∠BAC+∠EAD=180°,
∴∠EAB+∠DAC=180°.
∵∠EAB+∠BAH=180°,
∴∠BAH=∠CAD.
在△ABH和△ACD中,
∴△ABH≌△ACD(SAS).
∴BH=DC.
∵AD=AE,AH=AD,
∴AE=AH.
∵EF=FB,
∴BH=2AF.
∴CD=2AF.
同步练习题
A组(基础题)
一、填空题
1.(1)从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是_____;
(2)一个十二边形的内角和等于_____.
2.(1)从多边形的一个顶点可以画出4条对角线,则该多边形的内角和为_____;
(2)一个多边形的内角和比三角形内角和的2倍多180°,这个多边形的边数是_____.
3.从正n边形的一个顶点可以画5条对角线,则这个n边形的每个内角的度数为_____度.
4.(1)若一个正n边形的每个内角为108°,则这个正n边形的所有对角线的条数是5;
(2)从n边形一个顶点出发共有8条对角线,则这些对角线把原多边形分成_____个三角形.
二、选择题
5.多边形的内角和不可能为(
)
A.180°
B.540°
C.1
080°
D.1
200°
6.如果从多边形的一个顶点可以画出a条对角线,那么这a条对角线把该多边形分成的三角形的个数为(
)
A.a
B.a-3
C.a-2
D.a+1
7.(n+2)边形的内角和比n边形的内角和大(
)
A.180°
B.360°
C.n·180°
D.n·360°
8.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的内角和为(
)
A.540°
B.720°
C.900°
D.1
260°
三、解答题
9.(1)一个多边形的内角和比四边形的内角和多360°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
(2)已知一个多边形的内角和与外角和相加为1
800°,求这个多边形的对角线的条数.
10.若一个多边形的内角和是它的外角和的5倍,求这个多边形的边数和对角线的条数.
B组(中档题)
一、填空题
11.如图为矩形ABCD,一条直线将该矩形分割成两个多边形.若这两个多边形的内角和分别为a和b,则a+b=_____.
12.将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在点E′,D处.已知∠AFC=76°,则∠CFD′=_____.
13.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB的度数为_____.
二、解答题
14.(1)如图,M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
①求证:△ABM≌△BCN;
②求∠APN的度数.
(2)如图,在四边形ABCD中,AC,BD相交于点O,E,F分别是AD,BC的中点,EF分别交AC,BD于点M,N,且OM=ON.求证:AC=BD.
C组(综合题)
15.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图1,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图2说明理由.
参考答案
2020-2021学年北师大版八年级数学下册第六章6.4.1多边形的内角和与外角和(一)
同步练习题
A组(基础题)
一、填空题
1.(1)从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是8;
(2)一个十二边形的内角和等于1_800°.
2.(1)从多边形的一个顶点可以画出4条对角线,则该多边形的内角和为900°;
(2)一个多边形的内角和比三角形内角和的2倍多180°,这个多边形的边数是5.
3.从正n边形的一个顶点可以画5条对角线,则这个n边形的每个内角的度数为135度.
4.(1)若一个正n边形的每个内角为108°,则这个正n边形的所有对角线的条数是5;
(2)从n边形一个顶点出发共有8条对角线,则这些对角线把原多边形分成9个三角形.
二、选择题
5.多边形的内角和不可能为(D)
A.180°
B.540°
C.1
080°
D.1
200°
6.如果从多边形的一个顶点可以画出a条对角线,那么这a条对角线把该多边形分成的三角形的个数为(D)
A.a
B.a-3
C.a-2
D.a+1
7.(n+2)边形的内角和比n边形的内角和大(B)
A.180°
B.360°
C.n·180°
D.n·360°
8.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的内角和为(C)
A.540°
B.720°
C.900°
D.1
260°
三、解答题
9.(1)一个多边形的内角和比四边形的内角和多360°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形的边数为n,则
(n-2)·180°=360°+360°,解得n=6.
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为(360+360)÷6=120.
故这个多边形的每个内角是120°.
(2)已知一个多边形的内角和与外角和相加为1
800°,求这个多边形的对角线的条数.
解:设这个多边形是n边形,则(n-2)×180°=1
800°-360°,
解得n=10.
∴这个多边形的对角线的条数为10×(10-3)÷2=35(条).
10.若一个多边形的内角和是它的外角和的5倍,求这个多边形的边数和对角线的条数.
解:设这个多边形的边数为n,依题意,得
(n-2)·180°=5×360°,解得n=12.
则对角线的条数为=54(条).
∴这个多边形的边数是12,对角线的条数为54.
B组(中档题)
一、填空题
11.如图为矩形ABCD,一条直线将该矩形分割成两个多边形.若这两个多边形的内角和分别为a和b,则a+b=360°或540°或720°.
12.将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在点E′,D处.已知∠AFC=76°,则∠CFD′=28°.
13.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB的度数为108°.
二、解答题
14.(1)如图,M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
①求证:△ABM≌△BCN;
②求∠APN的度数.
解:①证明:∵ABCDE是正五边形,
∴AB=BC,∠ABM=∠C.
在△ABM和△BCN中,
∴△ABM≌△BCN(SAS).
②∵△ABM≌△BCN,
∴∠BAM=∠CBN.
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°.
∴∠APN=108°.
(2)如图,在四边形ABCD中,AC,BD相交于点O,E,F分别是AD,BC的中点,EF分别交AC,BD于点M,N,且OM=ON.求证:AC=BD.
证明:取AB和CD的中点G和H,连接EG,GF,FH,EH,则EH∥AC,EH=AC,HF∥BD,FH=BD,GE∥BD,
∴∠3=∠2,∠1=∠4.
∵OM=ON,
∴∠1=∠2.
∴∠4=∠3=∠1=∠2.
同理:∠EFH=∠GFE=∠1=∠2.
∴∠4=∠EFH.
∴EH=HF.
∵EH=AC,FH=BD,
∴AC=BD.
C组(综合题)
15.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图1,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图2说明理由.
解:(1)证明:∵∠BAC+∠EAD=180°,∠BAE=90°,
∴∠DAC=90°.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
∴BE=CD.
∵在Rt△ABE中,F为BE的中点,
∴BE=2AF.
∴CD=2AF.
(2)成立.
证明:延长EA交BC于点G,在AG上截取AH=AD.
∵∠BAC+∠EAD=180°,
∴∠EAB+∠DAC=180°.
∵∠EAB+∠BAH=180°,
∴∠BAH=∠CAD.
在△ABH和△ACD中,
∴△ABH≌△ACD(SAS).
∴BH=DC.
∵AD=AE,AH=AD,
∴AE=AH.
∵EF=FB,
∴BH=2AF.
∴CD=2AF.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
