2020-2021学年八年级数学人教版下册18.2.3.1正方形的性质与判定课件(共28张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.2.3.1正方形的性质与判定课件(共28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
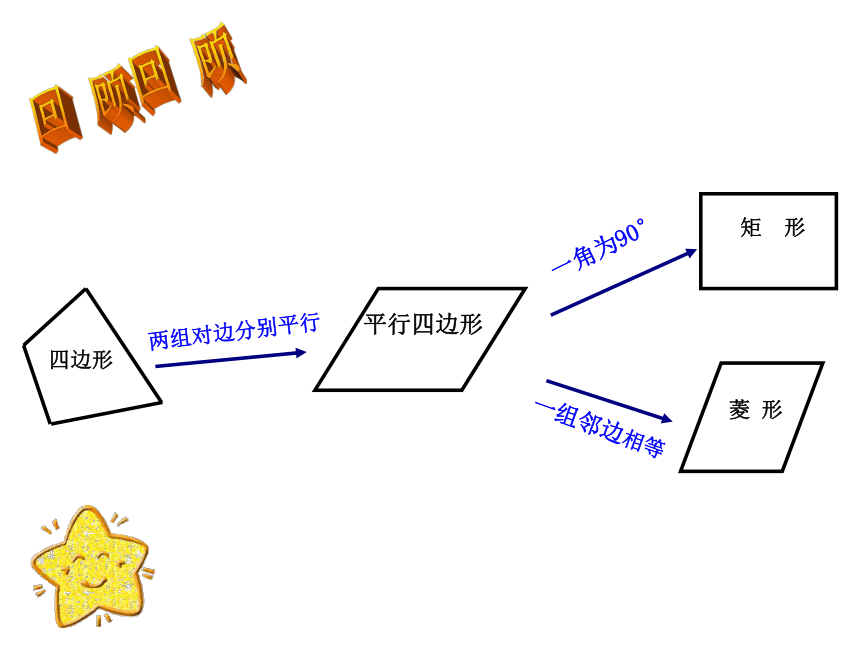
正方形
四边形
两组对边分别平行
平行四边形
矩
形
菱
形
一角为90°
一组邻边相等
回
顾
边
角
对
角
线
对
称
性
平
行
四边形
矩
形
菱
形
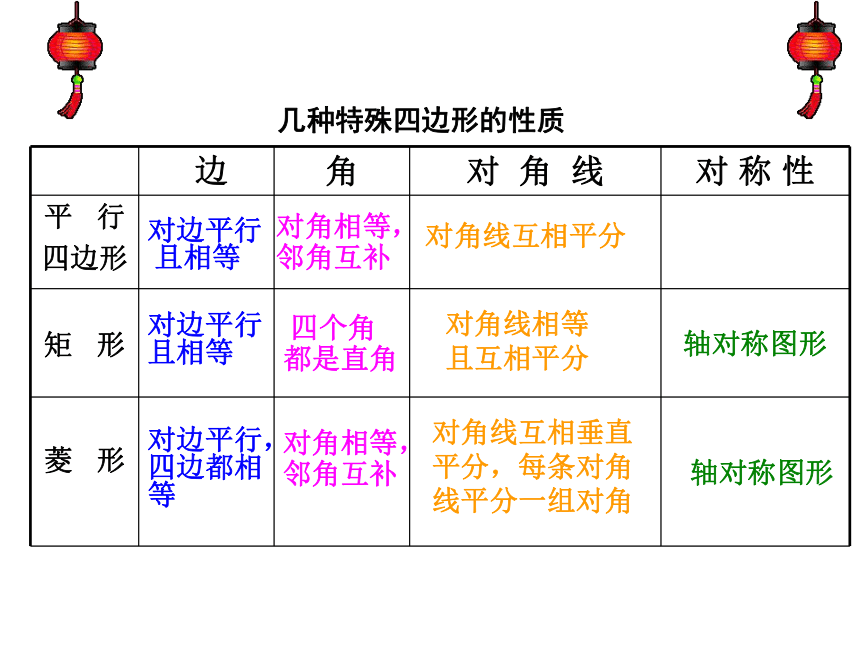
几种特殊四边形的性质
对边平行
且相等
对边平行
且相等
对边平行,四边都相等
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
轴对称图形
轴对称图形
矩
形
正方形
〃
〃
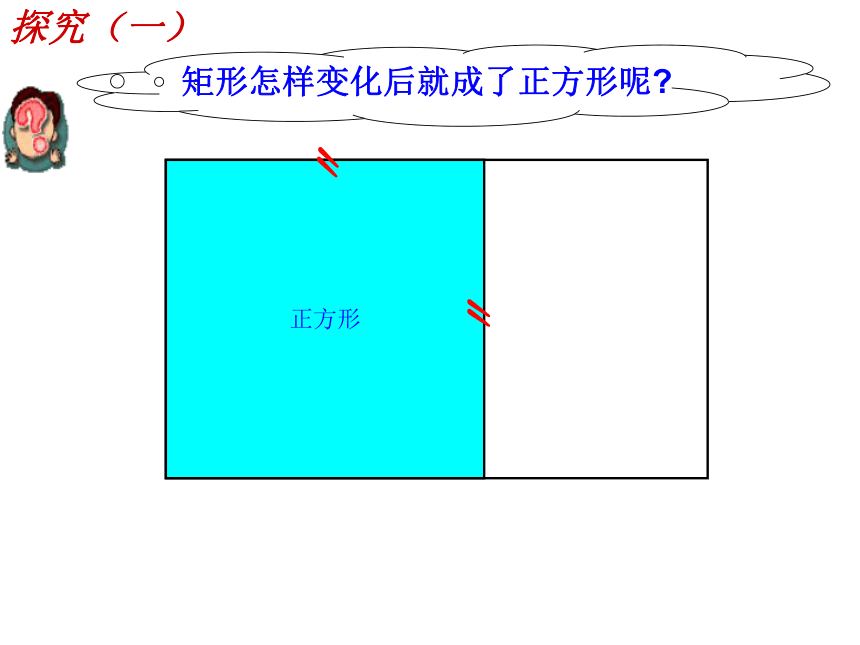
矩形怎样变化后就成了正方形呢?
探究(一)
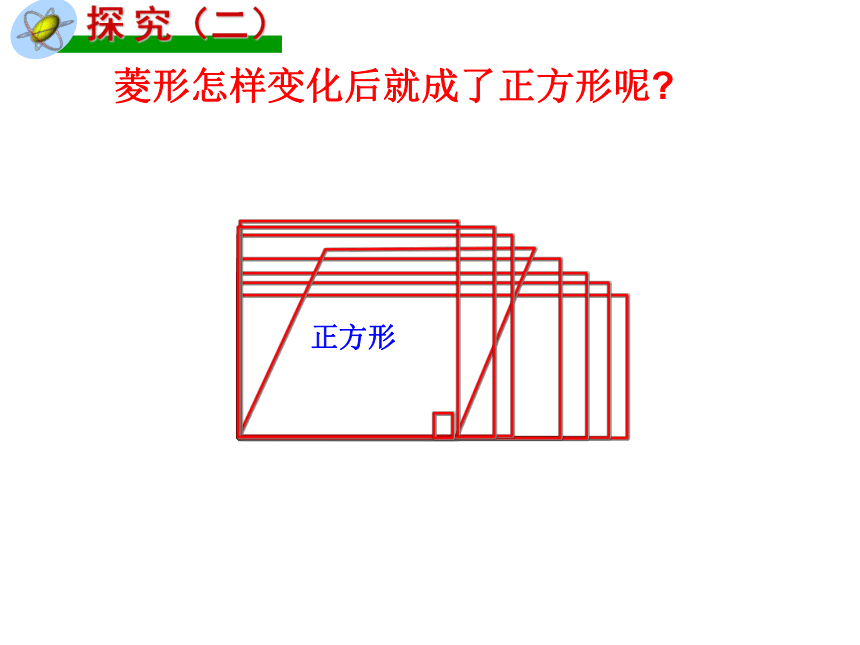
探
究(二)
菱形怎样变化后就成了正方形呢?
菱
形
探
究(二)
菱形怎样变化后就成了正方形呢?
正方形
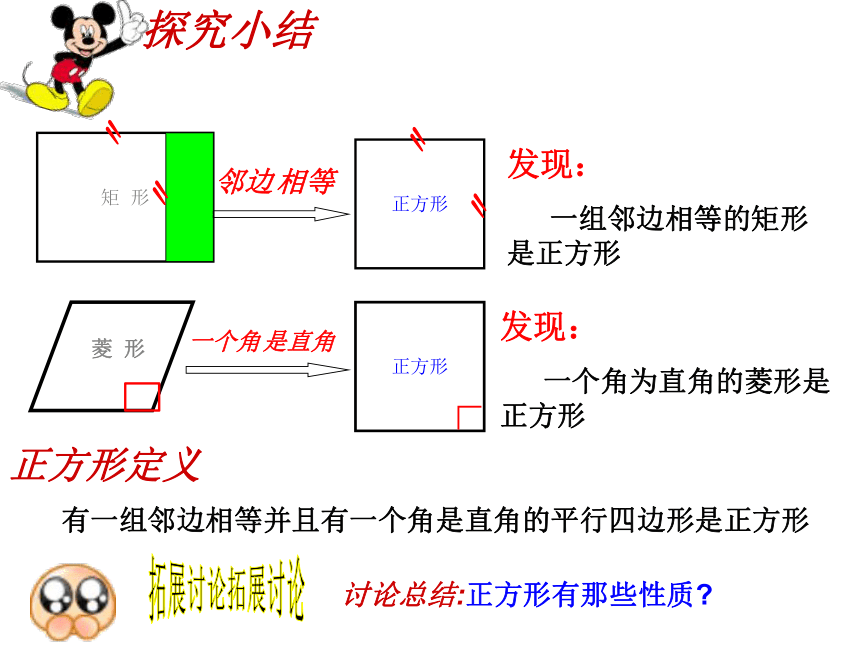
探究小结
矩
形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形
是正方形
菱
形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
拓展讨论
讨论总结:正方形有那些性质?
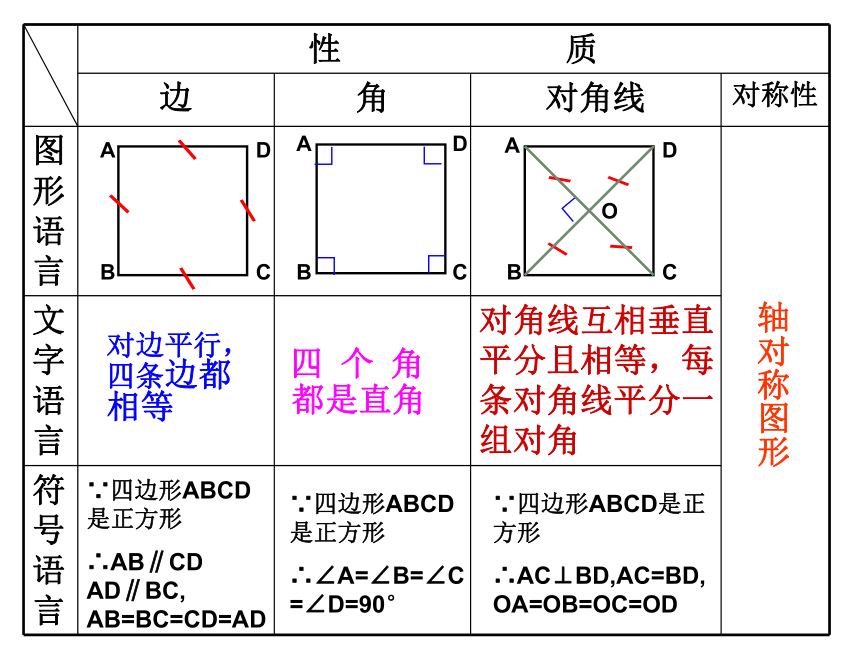
性
质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行,
四条边都相等
四
个
角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD
AD∥BC,
AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形
你觉得什么样的四边形是正方形呢?
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
有一组邻边相等
有一个角是直角
常
见
判
定
方
法
1.平行
四边形
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
例
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做?你会做吗?
第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对
角线AC、BD相交于点O.
求证:△ABO、
△BCO、
△CDO、
△DAO是全等的等腰直角三角形.
证明:
∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO、
△BCO、
△CDO、
△DAO都是等腰直角三角形,并且
△ABO≌
△BCO
≌
△CDO
≌
△DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、
△ADC、
△ABD、
△BCD
;
△AOB、
△BOC、
△COD、
△DOA.
1、要使一个菱形成为正方形需
增加的条件是
(填上一个条件即可)
小试牛刀
1、要使一个菱形成为正方形需
增加的条件是
有一个角是直角
或对角线相等
(填上一个条件即可)
小试牛刀
2、要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
2、要使一个矩形成为正方形需添加的条件是一组邻边相等或对
角线互相垂直
(填上一个条件即可)
下列正确的是
A.
四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
火眼金睛
下列正确的是
D
A.
四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
火眼金睛
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
用心学习,有所收获
平行四边形
有一组邻边相等
有一个角是直角
正方形
矩
形
有一组邻边相等
正方形
菱
形
有一个角是直角
正方形
3、正方形的判定
课后作业
P103
13题
P104
15题
谢谢
正方形
四边形
两组对边分别平行
平行四边形
矩
形
菱
形
一角为90°
一组邻边相等
回
顾
边
角
对
角
线
对
称
性
平
行
四边形
矩
形
菱
形
几种特殊四边形的性质
对边平行
且相等
对边平行
且相等
对边平行,四边都相等
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
轴对称图形
轴对称图形
矩
形
正方形
〃
〃
矩形怎样变化后就成了正方形呢?
探究(一)
探
究(二)
菱形怎样变化后就成了正方形呢?
菱
形
探
究(二)
菱形怎样变化后就成了正方形呢?
正方形
探究小结
矩
形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形
是正方形
菱
形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
拓展讨论
讨论总结:正方形有那些性质?
性
质
边
角
对角线
对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行,
四条边都相等
四
个
角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD
AD∥BC,
AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形
你觉得什么样的四边形是正方形呢?
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
有一组邻边相等
有一个角是直角
常
见
判
定
方
法
1.平行
四边形
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
例
求证:
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做?你会做吗?
第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对
角线AC、BD相交于点O.
求证:△ABO、
△BCO、
△CDO、
△DAO是全等的等腰直角三角形.
证明:
∵
四边形ABCD是正方形,
∴
AC=BD,AC⊥BD,AO=BO=CO=DO.
∴
△ABO、
△BCO、
△CDO、
△DAO都是等腰直角三角形,并且
△ABO≌
△BCO
≌
△CDO
≌
△DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、
△ADC、
△ABD、
△BCD
;
△AOB、
△BOC、
△COD、
△DOA.
1、要使一个菱形成为正方形需
增加的条件是
(填上一个条件即可)
小试牛刀
1、要使一个菱形成为正方形需
增加的条件是
有一个角是直角
或对角线相等
(填上一个条件即可)
小试牛刀
2、要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
2、要使一个矩形成为正方形需添加的条件是一组邻边相等或对
角线互相垂直
(填上一个条件即可)
下列正确的是
A.
四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
火眼金睛
下列正确的是
D
A.
四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
火眼金睛
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
用心学习,有所收获
平行四边形
有一组邻边相等
有一个角是直角
正方形
矩
形
有一组邻边相等
正方形
菱
形
有一个角是直角
正方形
3、正方形的判定
课后作业
P103
13题
P104
15题
谢谢
