2020-2021学年北师大版八年级数学下册第3章图形的平移与旋转经典好题优生辅导训练(word版含解析)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册第3章图形的平移与旋转经典好题优生辅导训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 285.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 17:28:48 | ||
图片预览



文档简介
2021年北师大版八年级数学下册第3章图形的平移与旋转经典好题优生辅导训练(附答案)
1.下列四个图形中既是中心对称图形又是轴对称图形的是( )
A.圆
B.等边三角形
C.平行四边形
D.正五边形
2.如图,平面内某正方形内有一长为10宽为5的矩形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10
B.11
C.12
D.13
3.如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50°
B.75°
C.65°
D.60°
4.点(4,3)经过某种图形变换后得到点B(4,﹣3),这种图形变换可以是( )
A.关于x轴对称
B.关于y轴对称
C.绕原点逆时针旋转90°
D.绕原点顺时针旋转90°
5.如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
A.70°
B.84°
C.80°
D.86°
6.如图,将△ABC绕顶点A顺时针旋转一个角度后,恰好AB′∥BC,若∠B=30°,则△ABC旋转了( )
A.10°
B.20°
C.30°
D.35°
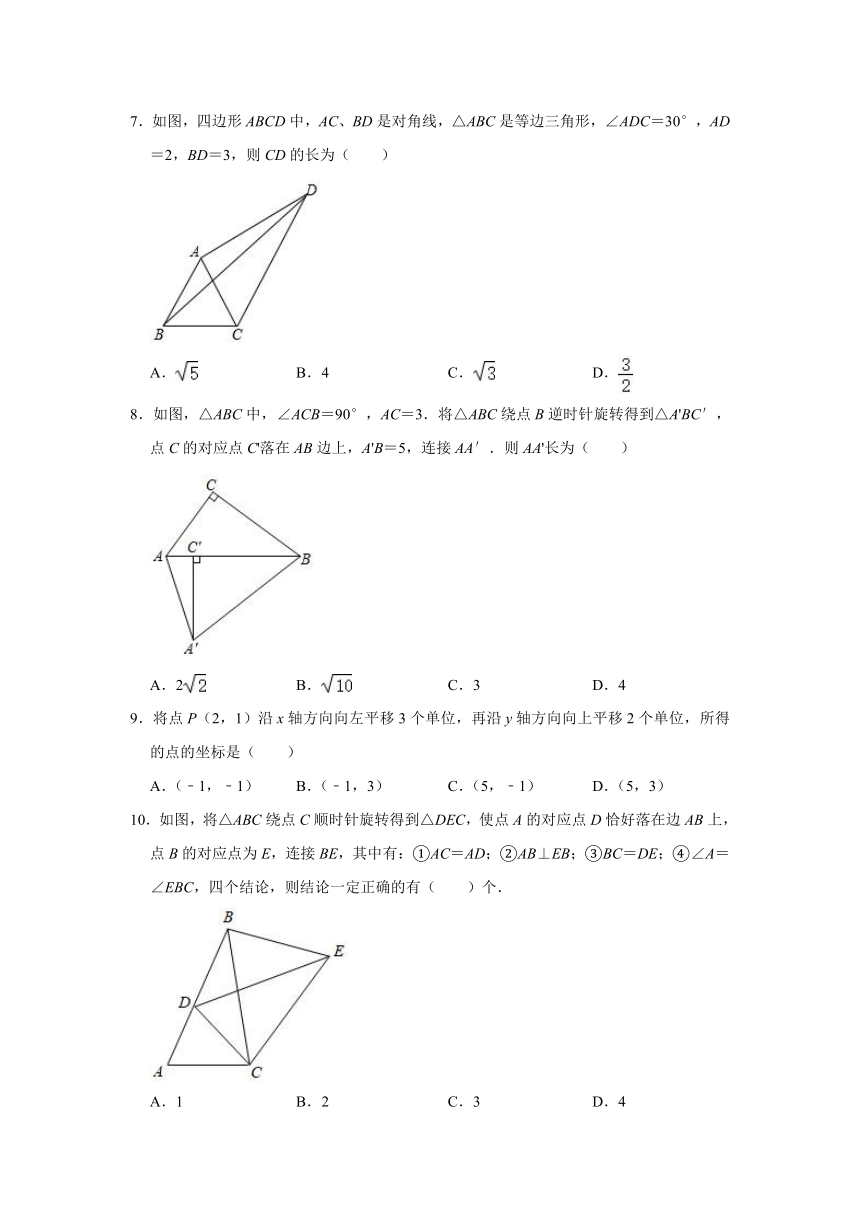
7.如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=2,BD=3,则CD的长为( )
A.
B.4
C.
D.
8.如图,△ABC中,∠ACB=90°,AC=3.将△ABC绕点B逆时针旋转得到△A'BC′,点C的对应点C'落在AB边上,A'B=5,连接AA′.则AA'长为( )
A.2
B.
C.3
D.4
9.将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是( )
A.(﹣1,﹣1)
B.(﹣1,3)
C.(5,﹣1)
D.(5,3)
10.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,其中有:①AC=AD;②AB⊥EB;③BC=DE;④∠A=∠EBC,四个结论,则结论一定正确的有( )个.
A.1
B.2
C.3
D.4
11.如图,在凸四边形ABCD中,∠BAD=∠BCD=120°,BC=CD=12cm,则线段AC的长等于
cm.
12.如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是
.
13.如图,将△ABC沿着射线BC的方向平移,得到△DEF.若EF=13,EC=8,则平移的距离为
.
14.已知点P(a﹣3,2﹣a)关于原点对称的点在第四象限,则a的取值范围是
.
15.如图,△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点B旋转得到△A'BC',且点C的对应点C'刚好落在AB上,连接AA'.则∠AA'C'=
.
16.如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分).道路的宽为2米,余下部分种植草坪.则草坪的面积为
平方米.
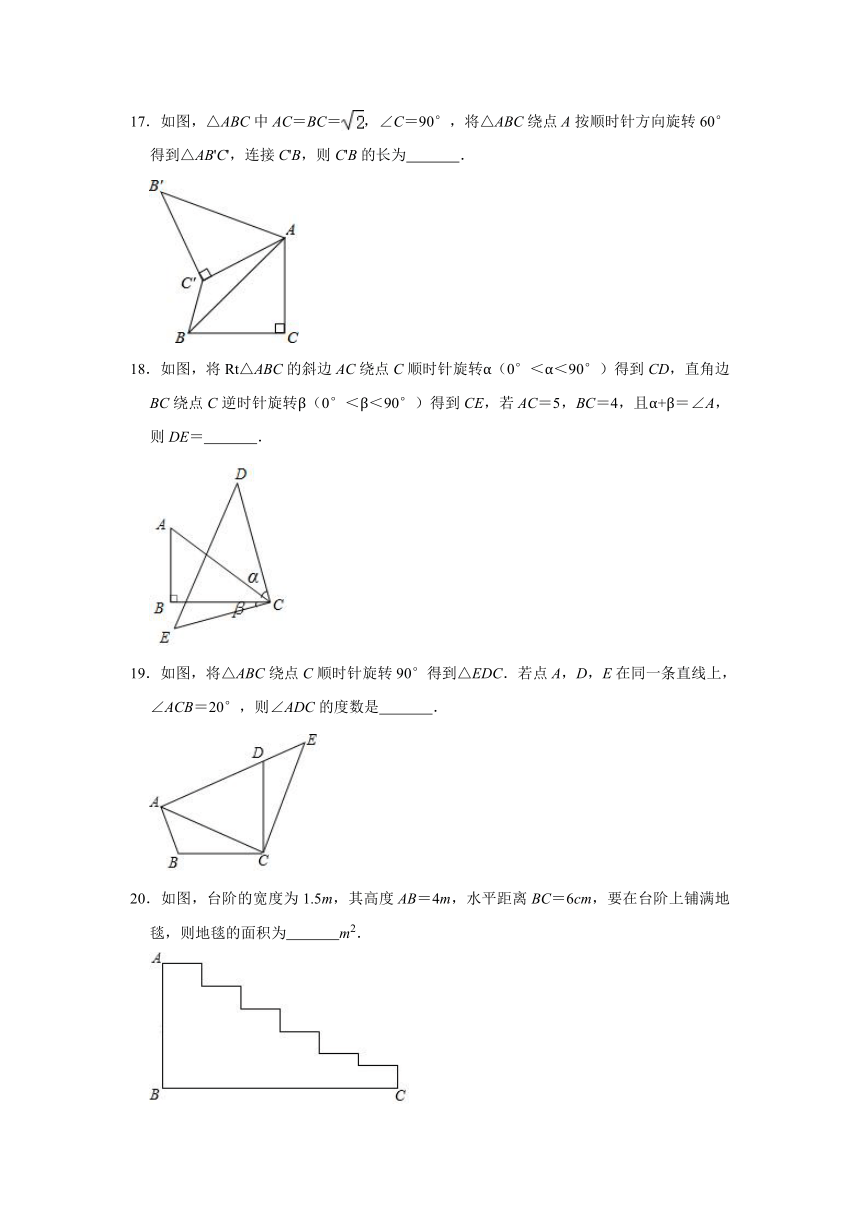
17.如图,△ABC中AC=BC=,∠C=90°,将△ABC绕点A按顺时针方向旋转60°得到△AB'C',连接C'B,则C'B的长为
.
18.如图,将Rt△ABC的斜边AC绕点C顺时针旋转α(0°<α<90°)得到CD,直角边BC绕点C逆时针旋转β(0°<β<90°)得到CE,若AC=5,BC=4,且α+β=∠A,则DE=
.
19.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是
.
20.如图,台阶的宽度为1.5m,其高度AB=4m,水平距离BC=6cm,要在台阶上铺满地毯,则地毯的面积为
m2.
21.如图,在△ABC中,∠C=90°,BC=a,AC=b,(b>a>0),将△ABC绕点B顺时针旋转90°得△A1BC1.
(1)画出△A1BC1.
(2)将△ABC沿射线CB方向平移,平移后得△A2B2C2.
①当平移距离等于a(点C2和点B重合)时,求四边形A1A2C2B2的面积.(用a,b的代数式表示)
②若a=1,b=2,当△A1A2C2的面积和△A1C2B2的面积相等时,平移距离多少?(直接写出答案)
22.如图,在四边形ABCD中,BC=CD,∠BCD=α°,∠ABC+∠ADC=180°,AC、BD交于点E.将△CBA绕点C顺时针旋转α°得到△CDF.
(1)画出旋转之后的图形;
(2)求证:∠CAB=∠CAD;
(3)若∠ABD=90°,AB=3,BD=4,△BCE的面积为S1,△CDE的面积为S2,求S1:S2的值.
23.在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;△A2B2C2可看作△A1B1C1以点(
,
)为旋转中心,旋转
°得到的.
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(﹣4,﹣2),请直接写出直线l的函数解析式.
24.如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:△AEB≌△ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
25.△ABC中,BC=8,以AC为边向外作等边△ACD.
(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;
(2)如图②,若∠ABC=60°,AB=4,求BD的长.
26.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:△BAP≌△CAQ.
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
参考答案
1.解:A、圆既是中心对称图形又是轴对称图形;
B、等边三角形是轴对称图形,但不是中心对称图形;
C、平行四边形是中心对称图形,但不是轴对称图形;
D、正五边形是轴对称图形,但不是中心对称图形;
故选:A.
2.解:∵矩形长为10宽为5,
∴矩形的对角线长为:==5,
∵矩形在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,
∴该正方形的边长不小于5,
∵11<5<12,
∴该正方形边长的最小正数n为12.
故选:C.
3.解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,
∴∠BAD=150°,AD=AB,∠E=∠ACB,
∵点B,C,D恰好在同一直线上,
∴△BAD是顶角为150°的等腰三角形,
∴∠B=∠BDA,
∴∠B=(180°﹣∠BAD)=15°,
∴∠E=∠ACB=180°﹣∠BAC﹣∠B=180°﹣100°﹣15°=65°,
故选:C.
4.解:∵点(4,3)关于x轴对称点的坐标为(4,﹣3),
∴点(4,3)经过某种图形变换后得到点B(4,﹣3),这种图形变换可以是关于x轴对称,
故选:A.
5.解:根据旋转的性质可知∠BAB1=100°,且AB=AB1,∠B=∠AB1C1.
∵点B1在线段BC的延长线上,∴∠BB1A=∠B=40°.
∴∠AB1C1=40°.
∴∠BB1C1=∠BB1A+∠AB1C1=40°+40°=80°.
故选:C.
6.解:∵AB′∥BC,
∴∠B'AB=∠B=30°.
则△ABC旋转了30°.
故选:C.
7.解:如图,在CD外侧作等边△CDE,连接AE,
则∠ADE=90°,DE=DC,∠DCE=60°,
∵∠ACB=∠DCE=60°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
∵,
∴△ACE≌△BCD(SAS),
∴AE=BD,
在Rt△ADE中,DE2=AE2﹣AD2=BD2﹣AD2=5,
∴DE=,
∴CD=,
故选:A.
8.解:根据旋转可知:
∠A′C′B=∠C=90°,A′C′=AC=3,AB=A′B=5,
根据勾股定理,得BC==4,
∴BC′=BC=4,
∴AC′=AB﹣BC′=1,
在Rt△AA′C′中,根据勾股定理,得
AA′==.故选:B.
9.解:将点P(2,1)沿x轴方向向左平移3个单位,
再沿y轴方向向上平移2个单位,所得的点的坐标是(﹣1,3).
故选:B.
10.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故①、③错误;
∴∠ACD=∠BCE,
∴∠A=∠ADC=(180°﹣∠ACD),∠CBE=(180°﹣∠BCE),
∴∠A=∠EBC,故④正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故②错误;
故选:A.
11.解:连接AC,
∵∠BAD=∠BCD=120°,BC=CD,
∴把△ACD绕点C按逆时针方向旋转120°得到△ECB,使CD与BC重合,
∴△ACD≌△ECB,∠ACE=120°,
∴AC=CE,BE=AD,∠CBE=∠D,
∵∠BAD=∠BCD=120°,
∴∠ABC+∠D=120°,
∴∠ABC+∠CBE=120°,即∠ABE=120°,
又∵△ABC是公共部分,
∴四边形ABCE和四边形ABCD全等,
∴AC=EC=BC=CD,
∵BC=CD=12cm,
∴AC=12cm.
故答案为:12.
12.解:∵AC=10,AO=3,
∴OC=7,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵线段OP绕点D逆时针旋转60°得到线段OD,要使点D恰好落在BC上,
∴OD=OP,∠POD=60°,
∵∠AOP+∠APO+∠A=180°,∠AOP+∠COD+∠POD=180°,
∴∠AOP+∠APO=120°,∠AOP+∠COD=120°,
∴∠APO=∠COD,
在△AOP和△CDO中,
,
∴△AOP≌△CDO(AAS),
∴AP=CO=7.
故答案为:7.
13.解:由平移的性质可知,△ABC≌△DEF,
∴BC=EF=13,
∴BE=BC﹣EC=13﹣8=5,
故答案为:5.
14.解:∵点P(a﹣3,2﹣a)关于原点对称的点在第四象限,
∴点P(a﹣3,2﹣a)在第二象限,
,
解得:a<2.
∴故答案为:a<2.
15.解:根据旋转可知:
∠A′BC=∠ABC=30°,A′B=AB,
∴∠BA′A=∠BAA′=(180°﹣30°)=75°,
∵∠BA′C=∠BAC=60°,
∴∠AA'C'=∠BA′A﹣∠BA′C=75°﹣60°=15°.
故答案为:15°.
16.解:草坪的面积为:(32﹣2)×(20﹣2)=540(平方米).
故答案为:540.
17.解:连接BB',延长BC′交AB'于点M,如图所示:
由旋转的性质得:∠BAB'=60°,BA=B'A,AC=BC=AC′=B′C′,∠AC′B′=∠ACB=90°,
∴△ABB'为等边三角形,
∴∠ABB'=60°,AB=BB',
在△ABC'与△B'BC'中,,
∴△ABC'≌△B'BC'(SSS)
∴∠MBB'=∠MBA=30°,
∴BM⊥AB',且AM=B'M,
∵AC=BC=,∠C=90°,
∴AB=AC=2,
∴AB=AB'=2,
∴AM=1,
BM===,
C′M=AB′=×2=1,
∴C′B=BM﹣C′M=﹣1,
故答案为:﹣1.
18.解:由旋转的性质可得CD=CA=5,CE=CB=4,
∵∠A+∠ACB=90°,且α+β=∠A,
∴∠ACB+α+β=90°
∴∠DCE=90°
∴DE===;
故答案为:.
19.解:根据旋转的性质可知∠DCE=∠ACB=20°,
∵AC=EC,∠ACE=90°,
∴∠E=45°.
∴∠ADC=∠DCE+∠E=20°+45°=65°.
故答案为65°.
20.解:∵台阶的高等于4米,台阶的长等于6米,宽等于1.5米,
∴地毯面积为:(4+6)×1.5=15(平方米).
故答案为:15.
21.解:(1)如图,△A1BC1即为所求;
(2)如图,△A2B2C2即为所求;
①如图1,四边形A1A2C2B2的面积:a2+b2;
②如图2,设平移的距离为h,
根据题意,b(a+b﹣h)=a2或b(h﹣a﹣b)=a2,
∵a=1,b=2,∴(1+2﹣h)=
∴(1+2﹣h)=或∴(h﹣3)=
∴h=2.5或3.5
∴平移距离为2.5或3.5.
22.解:(1)如图△CDF即为旋转之后的图形;
(2)证明:由旋转旋转可知:
△CAB≌△CFD,
∴∠CDF=∠CBA,∠F=∠CAB,CA=CF,
∵∠CBA+∠CDA=180°,
∴∠CDF+∠CDA=180°,
∴A、D、F三点共线,
∵AC=CF,
∴∠F=∠CAD,
∴∠CAB=∠CAD;
(3)过点E作EM⊥AF于点M,过点C作CN⊥BD于点N,
∴∠ABE=∠AME=90°,
在△ABE和△AME中,
,
∴△ABE≌△AME(AAS),
∴AM=AB=3,BE=ME,
∵∠ABD=90°,AB=3,BD=4,
∴AD==5
∴DM=2,设BE=EM=x,则DN=4﹣x
∴x2+22=(4﹣x)2,
解得x=1.5,
∴BE=1.5,DE=2.5,
∴S1:S2=BE?CN:DE?CN=.
23.解:(1)如图,△A1B1C1为所作,点C1的坐标(﹣1,2);
(2)如图,△A2B2C2为所作,C2(﹣3,﹣2);
△A2B2C2可看作△A1B1C1以点(2,0)为旋转中心,旋转180°得到的.
故答案为:﹣2,0,180°;
(3)因为A的坐标为(2,4),A3的坐标为(﹣4,﹣2),
所以直线l的函数解析式为y=﹣x.
24.解:(1)证明:∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
∵,
∴△EAB≌△DAC(SAS).
(2)如图,
∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形.
∴∠AED=60°,
∵△EAB≌△DAC
∴∠AEB=∠ADC=105°.
∴∠BED=45°.
25.解:(1)∵△ABE和△ACD都是等边三角形,
∴AE=AB,AC=AD=CD,∠EAB=∠DAC=∠ACD=60°,
∴∠EAB+∠BAC=∠DAC+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,,
∴△EAC≌△BAD(SAS),
∴CE=BD,
∵∠ACD=60°,∠ACB=30°,
∴∠BCD=90°,
在Rt△BCD中,∵CD=AC=6,BC=8,
∴BD===10,
∴CE=BD=10;
(2)取BC的中点E,连接AE,如图②所示:
∵BC=8,
∴BE=CE=BC=4,
∵AB=4,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴∠BAE=∠AEB=60°,AE=BE=4=CE,
∴△ACE是等腰三角形,
∴∠EAC=∠ECA,
∵∠AEB=∠EAC+∠ECA=60°,
∴∠EAC=∠ECA=30°,
∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠BCD=∠ECA+∠ACD=30°+60°=90°,∠BAC=∠EAC+∠BAE=30°+60°=90°,
由勾股定理得:AC=CD===4,
∴BD===4.
26.(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,,
∴△BAP≌△CAQ(SAS);
(2)解:∵由(1)得△APQ是等边三角形,
∴AP=PQ=3,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°﹣60°=90°,
∵PB=QC,
∴QC=4,
∴△PQC是直角三角形,
∴PC===5
1.下列四个图形中既是中心对称图形又是轴对称图形的是( )
A.圆
B.等边三角形
C.平行四边形
D.正五边形
2.如图,平面内某正方形内有一长为10宽为5的矩形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10
B.11
C.12
D.13
3.如图,△ABC中∠BAC=100°,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为( )
A.50°
B.75°
C.65°
D.60°
4.点(4,3)经过某种图形变换后得到点B(4,﹣3),这种图形变换可以是( )
A.关于x轴对称
B.关于y轴对称
C.绕原点逆时针旋转90°
D.绕原点顺时针旋转90°
5.如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
A.70°
B.84°
C.80°
D.86°
6.如图,将△ABC绕顶点A顺时针旋转一个角度后,恰好AB′∥BC,若∠B=30°,则△ABC旋转了( )
A.10°
B.20°
C.30°
D.35°
7.如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=2,BD=3,则CD的长为( )
A.
B.4
C.
D.
8.如图,△ABC中,∠ACB=90°,AC=3.将△ABC绕点B逆时针旋转得到△A'BC′,点C的对应点C'落在AB边上,A'B=5,连接AA′.则AA'长为( )
A.2
B.
C.3
D.4
9.将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是( )
A.(﹣1,﹣1)
B.(﹣1,3)
C.(5,﹣1)
D.(5,3)
10.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,其中有:①AC=AD;②AB⊥EB;③BC=DE;④∠A=∠EBC,四个结论,则结论一定正确的有( )个.
A.1
B.2
C.3
D.4
11.如图,在凸四边形ABCD中,∠BAD=∠BCD=120°,BC=CD=12cm,则线段AC的长等于
cm.
12.如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是
.
13.如图,将△ABC沿着射线BC的方向平移,得到△DEF.若EF=13,EC=8,则平移的距离为
.
14.已知点P(a﹣3,2﹣a)关于原点对称的点在第四象限,则a的取值范围是
.
15.如图,△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点B旋转得到△A'BC',且点C的对应点C'刚好落在AB上,连接AA'.则∠AA'C'=
.
16.如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分).道路的宽为2米,余下部分种植草坪.则草坪的面积为
平方米.
17.如图,△ABC中AC=BC=,∠C=90°,将△ABC绕点A按顺时针方向旋转60°得到△AB'C',连接C'B,则C'B的长为
.
18.如图,将Rt△ABC的斜边AC绕点C顺时针旋转α(0°<α<90°)得到CD,直角边BC绕点C逆时针旋转β(0°<β<90°)得到CE,若AC=5,BC=4,且α+β=∠A,则DE=
.
19.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是
.
20.如图,台阶的宽度为1.5m,其高度AB=4m,水平距离BC=6cm,要在台阶上铺满地毯,则地毯的面积为
m2.
21.如图,在△ABC中,∠C=90°,BC=a,AC=b,(b>a>0),将△ABC绕点B顺时针旋转90°得△A1BC1.
(1)画出△A1BC1.
(2)将△ABC沿射线CB方向平移,平移后得△A2B2C2.
①当平移距离等于a(点C2和点B重合)时,求四边形A1A2C2B2的面积.(用a,b的代数式表示)
②若a=1,b=2,当△A1A2C2的面积和△A1C2B2的面积相等时,平移距离多少?(直接写出答案)
22.如图,在四边形ABCD中,BC=CD,∠BCD=α°,∠ABC+∠ADC=180°,AC、BD交于点E.将△CBA绕点C顺时针旋转α°得到△CDF.
(1)画出旋转之后的图形;
(2)求证:∠CAB=∠CAD;
(3)若∠ABD=90°,AB=3,BD=4,△BCE的面积为S1,△CDE的面积为S2,求S1:S2的值.
23.在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;△A2B2C2可看作△A1B1C1以点(
,
)为旋转中心,旋转
°得到的.
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(﹣4,﹣2),请直接写出直线l的函数解析式.
24.如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:△AEB≌△ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
25.△ABC中,BC=8,以AC为边向外作等边△ACD.
(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;
(2)如图②,若∠ABC=60°,AB=4,求BD的长.
26.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:△BAP≌△CAQ.
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
参考答案
1.解:A、圆既是中心对称图形又是轴对称图形;
B、等边三角形是轴对称图形,但不是中心对称图形;
C、平行四边形是中心对称图形,但不是轴对称图形;
D、正五边形是轴对称图形,但不是中心对称图形;
故选:A.
2.解:∵矩形长为10宽为5,
∴矩形的对角线长为:==5,
∵矩形在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,
∴该正方形的边长不小于5,
∵11<5<12,
∴该正方形边长的最小正数n为12.
故选:C.
3.解:∵将△ABC绕点A逆时针旋转150°,得到△ADE,
∴∠BAD=150°,AD=AB,∠E=∠ACB,
∵点B,C,D恰好在同一直线上,
∴△BAD是顶角为150°的等腰三角形,
∴∠B=∠BDA,
∴∠B=(180°﹣∠BAD)=15°,
∴∠E=∠ACB=180°﹣∠BAC﹣∠B=180°﹣100°﹣15°=65°,
故选:C.
4.解:∵点(4,3)关于x轴对称点的坐标为(4,﹣3),
∴点(4,3)经过某种图形变换后得到点B(4,﹣3),这种图形变换可以是关于x轴对称,
故选:A.
5.解:根据旋转的性质可知∠BAB1=100°,且AB=AB1,∠B=∠AB1C1.
∵点B1在线段BC的延长线上,∴∠BB1A=∠B=40°.
∴∠AB1C1=40°.
∴∠BB1C1=∠BB1A+∠AB1C1=40°+40°=80°.
故选:C.
6.解:∵AB′∥BC,
∴∠B'AB=∠B=30°.
则△ABC旋转了30°.
故选:C.
7.解:如图,在CD外侧作等边△CDE,连接AE,
则∠ADE=90°,DE=DC,∠DCE=60°,
∵∠ACB=∠DCE=60°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
∵,
∴△ACE≌△BCD(SAS),
∴AE=BD,
在Rt△ADE中,DE2=AE2﹣AD2=BD2﹣AD2=5,
∴DE=,
∴CD=,
故选:A.
8.解:根据旋转可知:
∠A′C′B=∠C=90°,A′C′=AC=3,AB=A′B=5,
根据勾股定理,得BC==4,
∴BC′=BC=4,
∴AC′=AB﹣BC′=1,
在Rt△AA′C′中,根据勾股定理,得
AA′==.故选:B.
9.解:将点P(2,1)沿x轴方向向左平移3个单位,
再沿y轴方向向上平移2个单位,所得的点的坐标是(﹣1,3).
故选:B.
10.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故①、③错误;
∴∠ACD=∠BCE,
∴∠A=∠ADC=(180°﹣∠ACD),∠CBE=(180°﹣∠BCE),
∴∠A=∠EBC,故④正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故②错误;
故选:A.
11.解:连接AC,
∵∠BAD=∠BCD=120°,BC=CD,
∴把△ACD绕点C按逆时针方向旋转120°得到△ECB,使CD与BC重合,
∴△ACD≌△ECB,∠ACE=120°,
∴AC=CE,BE=AD,∠CBE=∠D,
∵∠BAD=∠BCD=120°,
∴∠ABC+∠D=120°,
∴∠ABC+∠CBE=120°,即∠ABE=120°,
又∵△ABC是公共部分,
∴四边形ABCE和四边形ABCD全等,
∴AC=EC=BC=CD,
∵BC=CD=12cm,
∴AC=12cm.
故答案为:12.
12.解:∵AC=10,AO=3,
∴OC=7,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵线段OP绕点D逆时针旋转60°得到线段OD,要使点D恰好落在BC上,
∴OD=OP,∠POD=60°,
∵∠AOP+∠APO+∠A=180°,∠AOP+∠COD+∠POD=180°,
∴∠AOP+∠APO=120°,∠AOP+∠COD=120°,
∴∠APO=∠COD,
在△AOP和△CDO中,
,
∴△AOP≌△CDO(AAS),
∴AP=CO=7.
故答案为:7.
13.解:由平移的性质可知,△ABC≌△DEF,
∴BC=EF=13,
∴BE=BC﹣EC=13﹣8=5,
故答案为:5.
14.解:∵点P(a﹣3,2﹣a)关于原点对称的点在第四象限,
∴点P(a﹣3,2﹣a)在第二象限,
,
解得:a<2.
∴故答案为:a<2.
15.解:根据旋转可知:
∠A′BC=∠ABC=30°,A′B=AB,
∴∠BA′A=∠BAA′=(180°﹣30°)=75°,
∵∠BA′C=∠BAC=60°,
∴∠AA'C'=∠BA′A﹣∠BA′C=75°﹣60°=15°.
故答案为:15°.
16.解:草坪的面积为:(32﹣2)×(20﹣2)=540(平方米).
故答案为:540.
17.解:连接BB',延长BC′交AB'于点M,如图所示:
由旋转的性质得:∠BAB'=60°,BA=B'A,AC=BC=AC′=B′C′,∠AC′B′=∠ACB=90°,
∴△ABB'为等边三角形,
∴∠ABB'=60°,AB=BB',
在△ABC'与△B'BC'中,,
∴△ABC'≌△B'BC'(SSS)
∴∠MBB'=∠MBA=30°,
∴BM⊥AB',且AM=B'M,
∵AC=BC=,∠C=90°,
∴AB=AC=2,
∴AB=AB'=2,
∴AM=1,
BM===,
C′M=AB′=×2=1,
∴C′B=BM﹣C′M=﹣1,
故答案为:﹣1.
18.解:由旋转的性质可得CD=CA=5,CE=CB=4,
∵∠A+∠ACB=90°,且α+β=∠A,
∴∠ACB+α+β=90°
∴∠DCE=90°
∴DE===;
故答案为:.
19.解:根据旋转的性质可知∠DCE=∠ACB=20°,
∵AC=EC,∠ACE=90°,
∴∠E=45°.
∴∠ADC=∠DCE+∠E=20°+45°=65°.
故答案为65°.
20.解:∵台阶的高等于4米,台阶的长等于6米,宽等于1.5米,
∴地毯面积为:(4+6)×1.5=15(平方米).
故答案为:15.
21.解:(1)如图,△A1BC1即为所求;
(2)如图,△A2B2C2即为所求;
①如图1,四边形A1A2C2B2的面积:a2+b2;
②如图2,设平移的距离为h,
根据题意,b(a+b﹣h)=a2或b(h﹣a﹣b)=a2,
∵a=1,b=2,∴(1+2﹣h)=
∴(1+2﹣h)=或∴(h﹣3)=
∴h=2.5或3.5
∴平移距离为2.5或3.5.
22.解:(1)如图△CDF即为旋转之后的图形;
(2)证明:由旋转旋转可知:
△CAB≌△CFD,
∴∠CDF=∠CBA,∠F=∠CAB,CA=CF,
∵∠CBA+∠CDA=180°,
∴∠CDF+∠CDA=180°,
∴A、D、F三点共线,
∵AC=CF,
∴∠F=∠CAD,
∴∠CAB=∠CAD;
(3)过点E作EM⊥AF于点M,过点C作CN⊥BD于点N,
∴∠ABE=∠AME=90°,
在△ABE和△AME中,
,
∴△ABE≌△AME(AAS),
∴AM=AB=3,BE=ME,
∵∠ABD=90°,AB=3,BD=4,
∴AD==5
∴DM=2,设BE=EM=x,则DN=4﹣x
∴x2+22=(4﹣x)2,
解得x=1.5,
∴BE=1.5,DE=2.5,
∴S1:S2=BE?CN:DE?CN=.
23.解:(1)如图,△A1B1C1为所作,点C1的坐标(﹣1,2);
(2)如图,△A2B2C2为所作,C2(﹣3,﹣2);
△A2B2C2可看作△A1B1C1以点(2,0)为旋转中心,旋转180°得到的.
故答案为:﹣2,0,180°;
(3)因为A的坐标为(2,4),A3的坐标为(﹣4,﹣2),
所以直线l的函数解析式为y=﹣x.
24.解:(1)证明:∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
∵,
∴△EAB≌△DAC(SAS).
(2)如图,
∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形.
∴∠AED=60°,
∵△EAB≌△DAC
∴∠AEB=∠ADC=105°.
∴∠BED=45°.
25.解:(1)∵△ABE和△ACD都是等边三角形,
∴AE=AB,AC=AD=CD,∠EAB=∠DAC=∠ACD=60°,
∴∠EAB+∠BAC=∠DAC+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,,
∴△EAC≌△BAD(SAS),
∴CE=BD,
∵∠ACD=60°,∠ACB=30°,
∴∠BCD=90°,
在Rt△BCD中,∵CD=AC=6,BC=8,
∴BD===10,
∴CE=BD=10;
(2)取BC的中点E,连接AE,如图②所示:
∵BC=8,
∴BE=CE=BC=4,
∵AB=4,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴∠BAE=∠AEB=60°,AE=BE=4=CE,
∴△ACE是等腰三角形,
∴∠EAC=∠ECA,
∵∠AEB=∠EAC+∠ECA=60°,
∴∠EAC=∠ECA=30°,
∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠BCD=∠ECA+∠ACD=30°+60°=90°,∠BAC=∠EAC+∠BAE=30°+60°=90°,
由勾股定理得:AC=CD===4,
∴BD===4.
26.(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,,
∴△BAP≌△CAQ(SAS);
(2)解:∵由(1)得△APQ是等边三角形,
∴AP=PQ=3,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°﹣60°=90°,
∵PB=QC,
∴QC=4,
∴△PQC是直角三角形,
∴PC===5
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
