2020-2021学年北师大版八年级下册2.6.2 一元一次不等式组 课件(共19张ppt)
文档属性
| 名称 | 2020-2021学年北师大版八年级下册2.6.2 一元一次不等式组 课件(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 218.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
2.6
一元一次不等式组
(第2课时)
学习目标
1.解较复杂的一元一次不等式组.
2.能根据具体问题中的数量关系,得出一元一次不等式组,解决简单的实际问题,并能根据实际问题的实际意义,检验结果是否符合题意
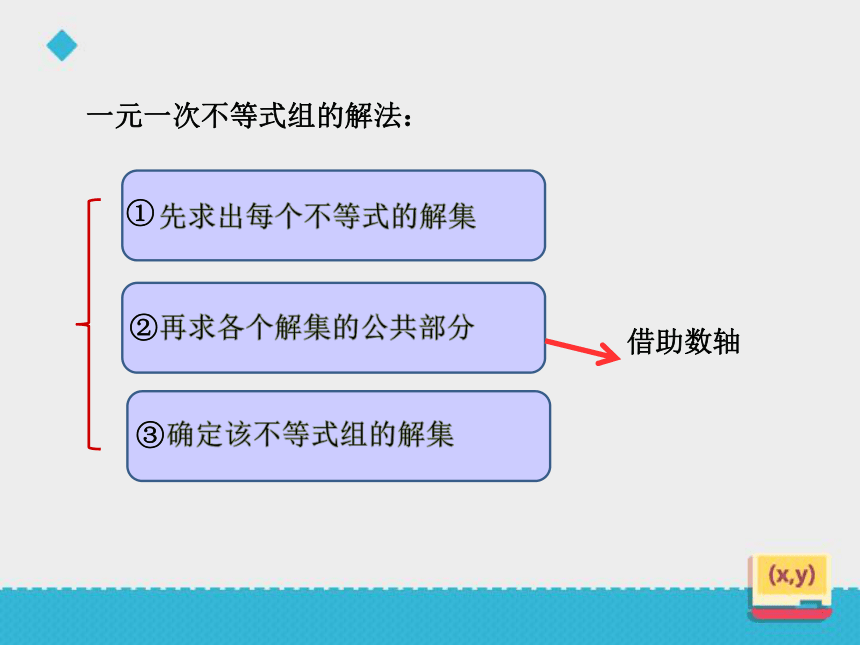
先求出每个不等式的解集
①
再求各个解集的公共部分
②
确定该不等式组的解集
③
借助数轴
一元一次不等式组的解法:
设a<b
在数轴上表示解
解集
x>a
x>b
x<a
x<b
x>a
x<b
x<a
x>b
a
b
a
b
a
b
a
b
x>b
x<a
无解
a<x<b
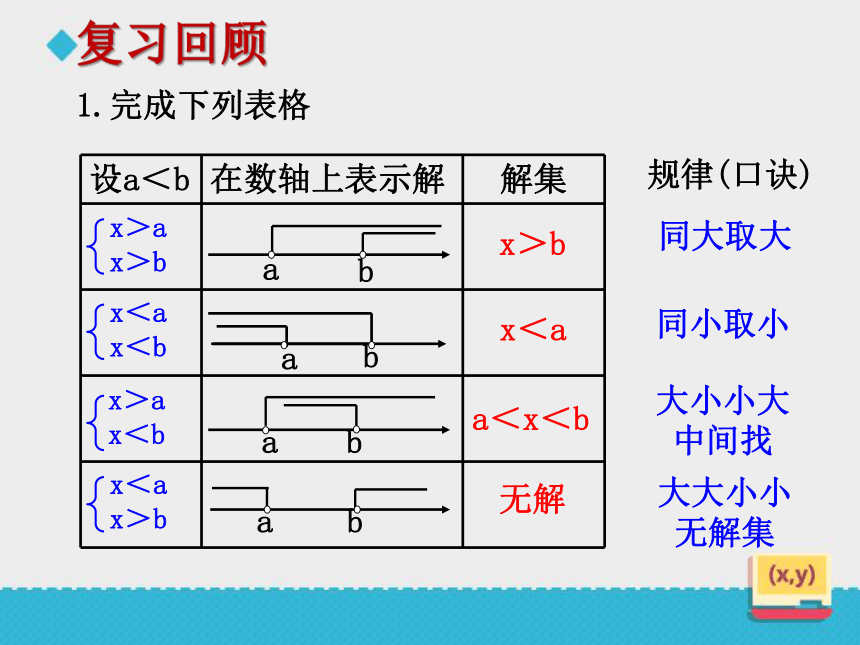
大小小大
中间找
大大小小
无解集
同小取小
同大取大
规律(口诀)
1.完成下列表格
复习回顾
⑴不等式组
的解集是__________
⑵不等式组
⑶不等式组
⑷不等式组
的解集是__________
的解集是__________
的解集是__________
无解
复习回顾
1.解不等式:
解法一:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
复习回顾
解法二:
所以不等式组的解集为:
知识点
1
较复杂的一元一次不等式组的解法
探究新知
例1、解不等式组
解:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
解不等式③得:
知识点
2
探究新知
解含字母的一元一次不等式(组)
题型一:已知解集求参数的值
例2.若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解:
解不等式①,得,x>m-2
解不等式②,得,x
<
n
+
1
因为不等式组有解,所以
m-2
<x<
n
+
1
又因为-1<
x
<2
所以
m=1
n=1
-1
2
< x <
m-2
n
+
1
m-2=
-1,
n
+
1
=
2
这里是一个含x的一元一次不等式组,将m,n看作两个已知数,求不等式的解集
题型二:已知解集的情况求参数的取值范围
探究新知
例3:若关于x的不等式组
练习:设关于x的不等式组
无解,求m的取值范围.
有实数解,
A.a<4
B.a≤4
C.a>4
D.a≥4
则a的取值范围是( )
题型三:已知整数解的情况求参数的值或取值范围
探究新知
例4:如果关于x的不等式组
只有3个整数解,求a的取值范围.
练习1:已知关于x的不等式组
有且只有三个整数解,求a的取值范围.
练习2:若关于x的不等式组
的所有整数解的和是-7,则m的取值范围是_____________________.?
-3练习3:已知关于x的不等式组
的整数解共有5个,则m的取值范围____________.
x-m≥0
5-2x>1
-4<m≤-3
方法总结:(数形结合)
1、把
表示在数轴上.
2、让
在数轴上
,观察找出满足
题目要求的
.
3、注意用假设法验证
能否取到.(带入原题)
已知或能算出的解
带字母的解
大概范围
临界点
移动
总结:求解含字母的不等式时一定要借助数轴分析
一元一次不等式组的应用
知识点
3
探究新知
例5:(1)在什么条件下,长度为3cm
,
7cm
,
xcm的三条线段可以围成一个三角形?
(2)已知三个数a-1,3-a,2a在数轴上所对应的点从左到右依次排列,你能确定a的取值范围吗?
(3)把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本,则共有学生人数为
(
)
A.6人
B.5人
C.6人或5人
D.4人
A
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例6:
用若干辆载重量为
8
t
的汽车运一批货物,若每辆汽车只装
4
t
,则剩下
20
t
货物;若每辆汽车装满
8
t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x
辆汽车,则这批货物共有(4x+20
)t.依题意得
解不等式组,得5<x
<7.
探究新知
例7:我校八(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36
kg,乙种制作材料29
kg,制作A,B两种型号的陶艺品用料情况如表所示:
需甲种材料
需乙种材料
1件A型陶艺品
0.9
kg
0.3
kg
1件B型陶艺品
0.4
kg
1
kg
(1)设制作B型陶艺品x件,求x的取值范围.
(2)请你根据学校现有的材料,分别写出八(2)班制作A型和B型陶艺品的件数.
解:(1)由题意知:
解不等式组得:18≤x≤20.
(2)A型32件,B型18件;A型31件,B型19件;A型30件,B型20件.
(3)若1件A型陶艺品和1件B型陶艺品销售获利分别为10元和15元,利用函数的性质,请分析说明如何制作获得的利润最大,最大利润为多少元?
(3)设获得的总利润为y元,
由题意知:y=10(50-x)+15x=5x+500
.
∵5>0,∴y随x的增大而增大.
则当x=20时,y最大值=600元.
故制作A型陶艺品30件,B型陶艺品20件时,
获得的利润最大为600元.
列一元一次不等式组解应用题的一般步骤:
(1)审:审题,分析题目中已知什么,求什么,
明确各数量之间的关系
(2)设:设适当的未知数
(3)找:找出题目中的所有不等关系
(4)列:列不等式组
(5)解:求出不等式组的解集
(6)答:写出符合题意的答案
知识归纳
本课小结
应用一元一次不等式组解决实际问题的一般思路:
实际问题
不等关系
不等式
不等式组
结合实际因素
找出
列出
组成
求
解
解决
2.6
一元一次不等式组
(第2课时)
学习目标
1.解较复杂的一元一次不等式组.
2.能根据具体问题中的数量关系,得出一元一次不等式组,解决简单的实际问题,并能根据实际问题的实际意义,检验结果是否符合题意
先求出每个不等式的解集
①
再求各个解集的公共部分
②
确定该不等式组的解集
③
借助数轴
一元一次不等式组的解法:
设a<b
在数轴上表示解
解集
x>a
x>b
x<a
x<b
x>a
x<b
x<a
x>b
a
b
a
b
a
b
a
b
x>b
x<a
无解
a<x<b
大小小大
中间找
大大小小
无解集
同小取小
同大取大
规律(口诀)
1.完成下列表格
复习回顾
⑴不等式组
的解集是__________
⑵不等式组
⑶不等式组
⑷不等式组
的解集是__________
的解集是__________
的解集是__________
无解
复习回顾
1.解不等式:
解法一:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
复习回顾
解法二:
所以不等式组的解集为:
知识点
1
较复杂的一元一次不等式组的解法
探究新知
例1、解不等式组
解:
解不等式①得:
解不等式②得:
所以不等式组的解集为:
解不等式③得:
知识点
2
探究新知
解含字母的一元一次不等式(组)
题型一:已知解集求参数的值
例2.若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解:
解不等式①,得,x>m-2
解不等式②,得,x
<
n
+
1
因为不等式组有解,所以
m-2
<x<
n
+
1
又因为-1<
x
<2
所以
m=1
n=1
-1
2
< x <
m-2
n
+
1
m-2=
-1,
n
+
1
=
2
这里是一个含x的一元一次不等式组,将m,n看作两个已知数,求不等式的解集
题型二:已知解集的情况求参数的取值范围
探究新知
例3:若关于x的不等式组
练习:设关于x的不等式组
无解,求m的取值范围.
有实数解,
A.a<4
B.a≤4
C.a>4
D.a≥4
则a的取值范围是( )
题型三:已知整数解的情况求参数的值或取值范围
探究新知
例4:如果关于x的不等式组
只有3个整数解,求a的取值范围.
练习1:已知关于x的不等式组
有且只有三个整数解,求a的取值范围.
练习2:若关于x的不等式组
的所有整数解的和是-7,则m的取值范围是_____________________.?
-3
的整数解共有5个,则m的取值范围____________.
x-m≥0
5-2x>1
-4<m≤-3
方法总结:(数形结合)
1、把
表示在数轴上.
2、让
在数轴上
,观察找出满足
题目要求的
.
3、注意用假设法验证
能否取到.(带入原题)
已知或能算出的解
带字母的解
大概范围
临界点
移动
总结:求解含字母的不等式时一定要借助数轴分析
一元一次不等式组的应用
知识点
3
探究新知
例5:(1)在什么条件下,长度为3cm
,
7cm
,
xcm的三条线段可以围成一个三角形?
(2)已知三个数a-1,3-a,2a在数轴上所对应的点从左到右依次排列,你能确定a的取值范围吗?
(3)把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本,则共有学生人数为
(
)
A.6人
B.5人
C.6人或5人
D.4人
A
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例6:
用若干辆载重量为
8
t
的汽车运一批货物,若每辆汽车只装
4
t
,则剩下
20
t
货物;若每辆汽车装满
8
t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x
辆汽车,则这批货物共有(4x+20
)t.依题意得
解不等式组,得5<x
<7.
探究新知
例7:我校八(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36
kg,乙种制作材料29
kg,制作A,B两种型号的陶艺品用料情况如表所示:
需甲种材料
需乙种材料
1件A型陶艺品
0.9
kg
0.3
kg
1件B型陶艺品
0.4
kg
1
kg
(1)设制作B型陶艺品x件,求x的取值范围.
(2)请你根据学校现有的材料,分别写出八(2)班制作A型和B型陶艺品的件数.
解:(1)由题意知:
解不等式组得:18≤x≤20.
(2)A型32件,B型18件;A型31件,B型19件;A型30件,B型20件.
(3)若1件A型陶艺品和1件B型陶艺品销售获利分别为10元和15元,利用函数的性质,请分析说明如何制作获得的利润最大,最大利润为多少元?
(3)设获得的总利润为y元,
由题意知:y=10(50-x)+15x=5x+500
.
∵5>0,∴y随x的增大而增大.
则当x=20时,y最大值=600元.
故制作A型陶艺品30件,B型陶艺品20件时,
获得的利润最大为600元.
列一元一次不等式组解应用题的一般步骤:
(1)审:审题,分析题目中已知什么,求什么,
明确各数量之间的关系
(2)设:设适当的未知数
(3)找:找出题目中的所有不等关系
(4)列:列不等式组
(5)解:求出不等式组的解集
(6)答:写出符合题意的答案
知识归纳
本课小结
应用一元一次不等式组解决实际问题的一般思路:
实际问题
不等关系
不等式
不等式组
结合实际因素
找出
列出
组成
求
解
解决
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
