2020-2021学年北师大版数学七年级下册单元期末复习课件 第二章 相交线与平行线(共68张PPT)
文档属性
| 名称 | 2020-2021学年北师大版数学七年级下册单元期末复习课件 第二章 相交线与平行线(共68张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览







文档简介
第二章 相交线与平行线
章末复习
第二章 相交线与平行线
章末复习
知识框架
归纳整合
素养提升
中考链接
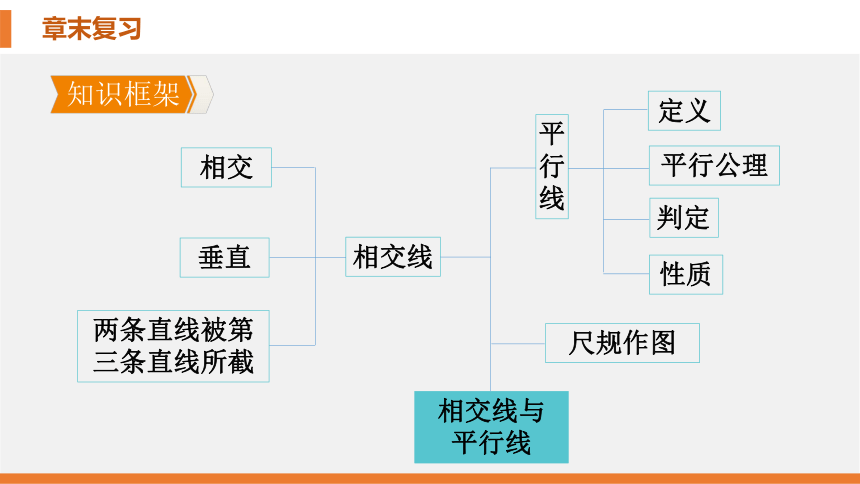
知识框架
相交线
相交线与
平行线
平行线
尺规作图
相交
垂直
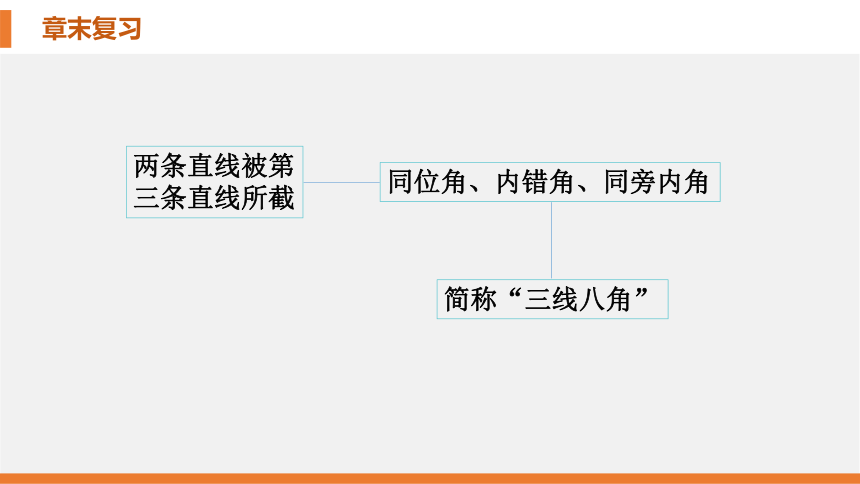
两条直线被第
三条直线所截
平行公理
判定
性质
定义
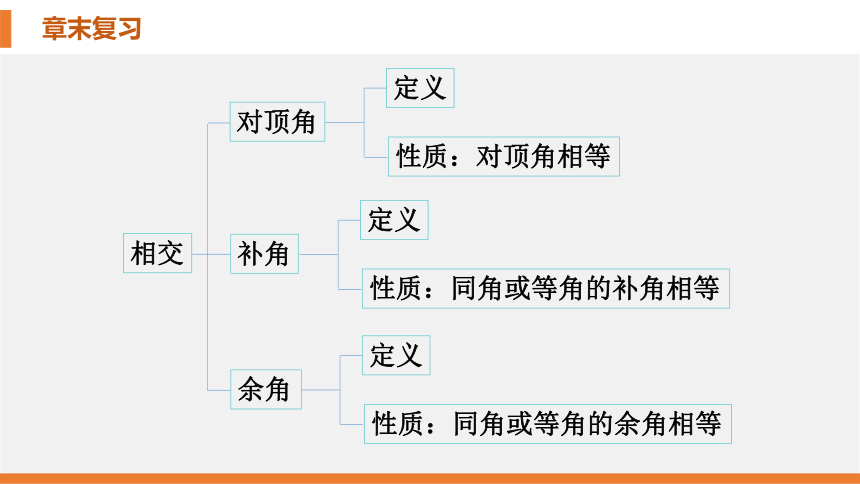
对顶角
补角
余角
相交
定义
性质:对顶角相等
定义
性质:同角或等角的补角相等
定义
性质:同角或等角的余角相等
平面内, 过一点有且只有一条直线与已知直线垂直
直线外一点与直线上各点连接的所有线段中, 垂线段最短
点到直线的距离
定义
垂直
两条直线被第
三条直线所截
同位角、内错角、同旁内角
简称“三线八角”
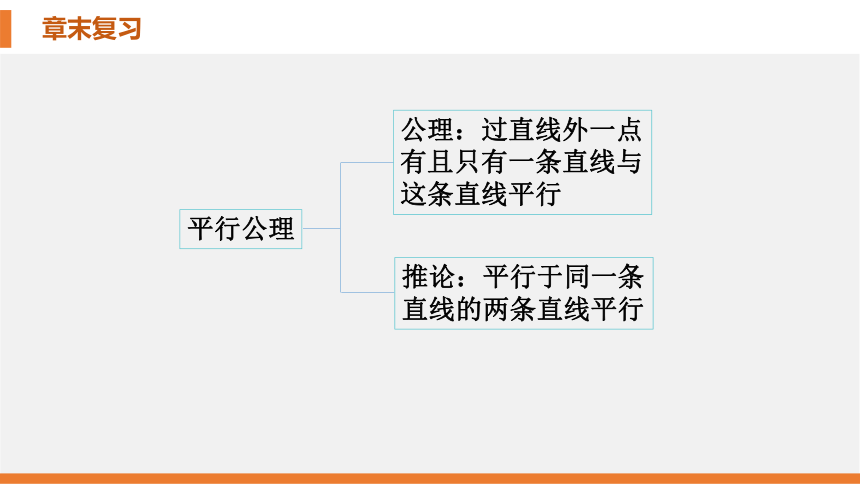
平行公理
公理:过直线外一点
有且只有一条直线与
这条直线平行
推论:平行于同一条
直线的两条直线平行
(1)同位角相等, 两直线平行
(2)内错角相等, 两直线平行
(3)同旁内角互补, 两直线平行
判定
(1)两直线平行, 同位角相等
(2)两直线平行, 内错角相等
(3)两直线平行, 同旁内角互补
性质
【要点指导】两条直线相交形成四个角, 这四个角中有两对对顶角、四对邻补角;当相交的两条直线互相垂直时, 相交形成的角是直角. 根据对顶角、邻补角之间的数量关系以及直角的定义, 可进行角度的相关计算.
归纳整合
专题一 两条直线相交构成的角的相关计算
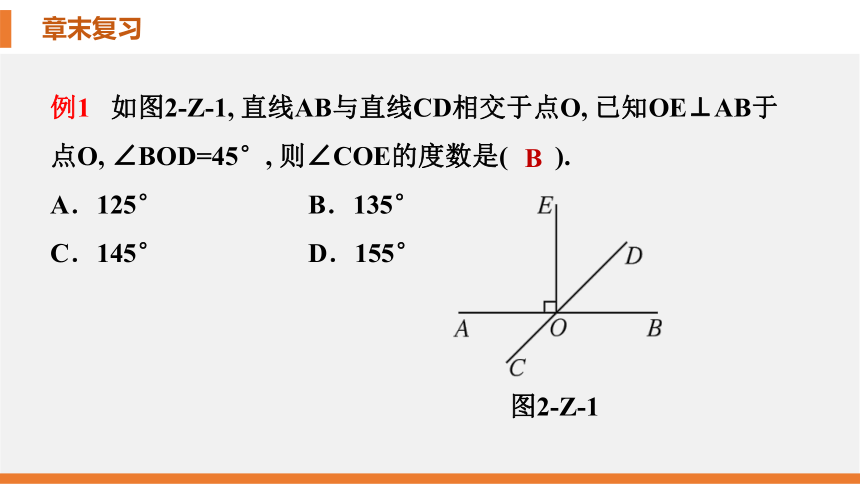
例1 如图2-Z-1, 直线AB与直线CD相交于点O, 已知OE⊥AB于点O, ∠BOD=45°, 则∠COE的度数是( ).
A.125° B.135°
C.145° D.155°
B
图2-Z-1
相关题1 如图2-Z-2, AB与CD相交于点O, OE⊥CD于点O, ∠BOE=54°, 则∠AOC= °.
36
图2-Z-2
[解析] 因为OE⊥CD,∠BOE=54°,
所以∠BOD=90°-∠BOE=90°-54°=36°.
又因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=36°.
【要点指导】直线外一点到这条直线的垂线段的长度叫作点到直线的距离, 这说明, 点到直线的距离可以转化为两点之间的距离.
专题二 关于两点之间、点与直线之间的距离
例2 如图2-Z-3所示, AB∥CD, DE⊥AB于点E, 经测量知AD=BC
=1.6 cm, DE=1.4 cm.
(1)BC的长表示什么之间的距离?
(2)点D到直线AB的距离是1.4 cm
还是1.6 cm?为什么?
图2-Z-3
解: (1)BC的长表示点B与点C之间的距离.
(2)点D到直线AB的距离是1.4 cm.
理由:
因为DE⊥AB ,
所以DE是点D到直线AB的垂线段,
所以点D到直线AB的距离是1.4 cm.
相关题2 如图2-Z-4, 已知长方形ABCD.
(1)点A与点C之间的距离是指线段 的长;
(2)点D到线段AB的距离是指线段 的长.
图2-Z-4
解: (1)AC (2)AD
例3 如图2-Z-5, 已知点A, B以及直线l.
(1)请画出从点A到直线l的最短路线, 并写出其依据;
(2)请在直线l上确定一点O, 使点O到点A, B的距离之和最短, 并写出其依据.
图2-Z-5
解: (1)如图2-Z-5所示, AE为点A到直线l的最短路线.
依据:直线外一点与直线上各点连接的所有线段中, 垂线段最短.
(2)如图2-Z-5所示, 连接AB, AB与直线l的交点O即为所求.
依据:两点之间, 线段最短.
图2-Z-5
相关题3 如图2-Z-6, 在三角形ABC中, ∠BCA=90°,BC=3, AC=4, AB=5, P是线段AB上的一个动点,求线段CP的最小值.
图2-Z-6
【要点指导】综合利用题目中角的数量关系判定两直线平行, 再根据平行线的性质得出另外一对相等或互补的角, 从而进行相关的计算或说理;或先通过平行线得出角的相等或互补关系, 再根据平行线的判定得出另一组直线互相平行.
专题三 与平行线性质、判定有关的计算与说理题
例4 已知:如图2-Z-7, AB∥CD, BD平分∠ABC, CE平分∠DCF, ∠ACE=90°.
(1)判断BD和CE的位置关系, 并说明理由;
(2)判断AC和BD是否垂直, 并说明理由.
图2-Z-7
解:(1)BD∥CE.
理由:因为AB∥CD, 所以∠ABC=∠DCF.
因为BD平分∠ABC, CE平分∠DCF,
所以∠2= ∠ABC, ∠4= ∠DCF,
所以∠2=∠4,所以BD∥CE(同位角相等, 两直线平行).
(2)AC⊥BD.
理由:因为BD∥CE, 所以∠DGC+∠ACE=180°.
因为∠ACE=90°, 所以∠DGC=180°-90°=90°,即AC⊥BD.
相关题4 如图2-Z-8, DE⊥AB,EF⊥BC, 垂足分别为E,F, 若∠B=∠ADE, 则AD与EF平行吗?若平行,请说明理由.
图2-Z-8
[解析] 因为已知EF⊥BC,
所以只需说明AD⊥BC即可证明AD∥EF.
而根据条件可说明∠BDE+∠ADE=90°,
则可得AD⊥BC.
解:AD∥EF.
理由:
因为DE⊥AB,所以∠BED=90°,所以∠B+∠BDE=90°.因为∠B=∠ADE,
所以∠BDE+∠ADE=90°,即∠ADB=90°,所以AD⊥BC.
所以∠EFD=∠ADC=90°,
所以AD∥EF.
【要点指导】垂直是特殊的相交, 在数学图形中, 平行和垂直经常同时出现, 解决问题时既要注意从线角关系的角度转化问题、推导出结论, 还要注意从线线关系的角度发现结论、转化问题, 多角度思考问题.
专题四 平行与垂直的综合运用
例5 如图2-Z-9, 已知AD⊥BC于点D, EG⊥BC于点G, ∠E=∠1, AD平分∠BAC吗?试说明理由.
图2-Z-9
解:AD平分∠BAC. 理由:如图2-Z-9,
因为AD⊥BC于点D, EG⊥BC于点G(已知),
所以∠ADC=∠EGC=90°(垂直的定义),
所以AD∥EG(同位角相等, 两直线平行),
所以∠1=∠2(两直线平行, 内错角相等),
∠E=∠3(两直线平行, 同位角相等).
又因为∠E=∠1(已知), 所以∠2=∠3(等量代换),
所以AD平分∠BAC(角平分线的定义).
图2-Z-9
相关题5 已知:如图2-Z-10,AB∥CD, OE平分∠AOD,OF⊥OE 于点O, ∠D=60°, 求∠BOF的度数.
图2-Z-10
解:因为AB∥CD,∠D=60°,
所以∠AOD=180°-∠D=180°-60°=120°,
∠BOD=∠D=60°.
因为OE平分∠AOD,
所以∠EOD=120°÷2=60°.
因为OF⊥OE于点O,所以∠EOF=90°,
所以∠DOF=90°-60°=30°,
所以∠BOF=∠BOD-∠DOF=60°-30°=30°.
【要点指导】在几何题中, 有些题目未给出图形, 这时我们就要结合题意先画出图形, 再解决问题. 这一过程常常具有多种符合题意的图形, 需要我们分类讨论解决.
素养提升
专题一 分类讨论思想
例1 已知一个角的两边与另一个角的两边分别平行, 则这两个角的数量关系为 .
相等或互补
分析 设两个角分别为∠1, ∠2, 根据题目信息可得有以下两种情况(图形画法不唯一):
由图2-Z-11可知∠1=∠2或∠1+∠2=180°,
即这两个角的数量关系为相等或互补.
图2-Z-11
相关题1 已知:∠BOC 在∠AOB的外部, OE平分∠AOB,OF平分∠BOC, OD平分∠AOC, ∠AOE=30°, ∠ B O D = 2 0 °, 试 求
∠COF的度数.
[解析]本题没有给出具体的图形, ∠AOB既可大于∠BOC,
又可小于∠BOC, 则应分这两种情况分别求解.
图①
图②
【要点指导】由本章的学习, 应该对转化这一数学思想有更深刻的体会. 这一思想在平行线与角的关系中表现特别明显.当我们要说明两条直线平行时, 经常把问题转化为说明两角相等或互补;当我们说明两角之间的数量关系时, 又经常将其转化为说明两直线平行.在几何推理中, 经常通过转化已知条件推出要求的结论, 必要时还需要添加辅助线进行转化.
专题二 转化思想
例2 [新乡长垣县期中] 如图2-Z-12①, E是直线AB, CD之间的一点,
AB∥CD, 连接EA, ED.
(1)探究猜想:
①若∠EAB=30°, ∠EDC=40°,
求∠AED的度数;
②若∠EAB=20°, ∠EDC=60°,
求∠AED的度数;
③猜想图①中∠AED, ∠EAB, ∠EDC之间的数量关系, 并说明理由.
图2-Z-12
(2)扩展应用:
如图②, 射线FE与长方形ABCD的边AB交于点E, 与边CD交于点F,
①②③④分别是被射线FE隔开的4个
区域(不含边界, 其中区域③④位于直
线AB的上方), P是位于以上四个区域
内的一点, 试猜∠PEB, ∠PFC, ∠EPF
之间的数量关系(不要求说明理由).
图2-Z-12
分析 (1)①过点E作EF∥AB, 再由平行线的性质即可得出结论;②, ③题根据①中的方法即可得出结论.
(2)当点P分别位于①, ②, ③, ④四个区域内时, 分别根据平行线的性质进行求解即可得出结论.
解:(1)如图2-Z-13①, 过点E作EF∥AB,
因为AB∥CD, 所以CD∥EF.
因为∠EAB=30°, ∠EDC=40°,
所以∠1=∠EAB=30°, ∠2=∠EDC=40°,
所以∠AED=∠1+∠2=70°.
图2-Z-13
②如图①, 过点E作EF∥AB,
因为AB∥CD,所以CD∥EF.
因为∠EAB=20°, ∠EDC=60°,
所以∠1=∠EAB=20°, ∠2=∠EDC=60°,
所以∠AED=∠1+∠2=80°.
图2-Z-13
③猜想:∠AED=∠EAB+∠EDC.
理由:如图①, 过点E作EF∥AB,
因为AB∥CD, 所以EF∥CD
(平行于同一条直线的两直线平行),
所以∠1=∠EAB, ∠2=∠EDC
(两直线平行, 内错角相等),
所以∠AED=∠1+∠2=∠EAB+∠EDC(等量代换).
图2-Z-13
(2)当点P在区域①内时, 如图②, ∠EPF=360°-(∠PEB+∠PFC);
当点P在区域②内时, 如图③, ∠EPF=∠PEB+∠PFC;
当点P在区域③内时, 如图④, ∠EPF=∠PEB-∠PFC;
当点P在区域④内时, 如图⑤, ∠EPF=∠PFC-∠PEB.
图2-Z-13
相关题2-1 [深圳龙岗区期末] 如图2-Z-14, 已知AB∥CD,BE平分∠ABC, DE平分∠ADC, ∠BAD=80°.
(1)求∠EDC的度数;
(2)若∠BCD=n°, 试求∠BED的度数(用含n的式子表示).
图2-Z-14
相关题2-2 [湘潭中考] 如图2-Z-15,E是AD延长线上一点,如果添加一个条件, 使BC∥AD, 则可添加的条件为 __________________
_________________________________________________________
. (任意添加一个符合题意的条件即可)
图2-Z-15
∠A+∠ABC=180°
或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE (答
案不唯一)
[解析]若∠A+∠ABC=180°,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD.
中考链接
母题1 (教材P40习题2.1第1题)
如图2-Z-16, 直线a, b相交, ∠1=38°, 求∠2,∠3, ∠4的度数.
图2-Z-16
考点:角的计算.
考情:一般以选择题、填空题的形式考查, 常考查计算某一个角的度数.
策略:对顶角的性质常与余角、补角结合在一起考查. 牢记性质:对顶角相等, 互补两角的和为180°, 互余两角的和为90°.
链接1 [泉州中考]如图2-Z-17, 直线AB与CD相交于点O. 若∠AOD=50°, 则∠BOC= °.
50
图2-Z-17
分析 因为∠BOC与∠AOD是对顶角,
所以∠BOC=∠AOD=50°.
母题2 (教材P43习题2.2第3题)
如图2-Z-18, 要把水渠中的水引到C点, 在渠岸AB的什么地方开沟, 才能使沟最短?画出图形, 并说明理由.
图2-Z-18
考点:点到直线的距离、垂线段最短.
考情:一般在选择题或者几何最值计算问题中考查.
策略:明确点到直线的距离是指垂线段的长度.
链接2 [厦门中考]如图2-Z-19, 三角形ABC是锐角三角形, 过点C作CD⊥AB, 垂足为D, 则点C到直线AB的距离是( ).
A.线段CA的长
B.线段CD的长
C.线段AD的长
D.线段AB的长
B
图2-Z-19
母题3 (教材P49习题2.4第2题)
如图2-Z-20 ,∠DAB+∠CDA=180°,∠ABC=∠1, 直线AB与CD平行吗?直线AD与BC呢?为什么?
图2-Z-20
考点:判定两直线平行的条件.
考情:主要考查两直线平行的判定,常在选择题中出现, 有时也作为解答题的一小问出现.
策略:根据两直线平行的判定方法:同位角相等, 两直线平行;内错角相等, 两直线平行;同旁内角互补, 两直线平行, 从而将角的数量关系转化为直线的位置关系.
链接3 [郴州中考]如图2-Z-21, 直线a, b被直线c所截, 下列条件中, 不能判定a∥b的是( ).
A.∠2=∠4 B.∠1+∠4=180°
C.∠5=∠4 D.∠1=∠3
D
分析 由∠2=∠4或∠1+∠4=180°
或∠5=∠4, 可得a∥b;
由∠1=∠3, 不能得到a∥b.
故选D.
图2-Z-21
母题4 (教材P54习题2.6第4题)
如图2-Z-22, AC∥ED,AB∥FD, ∠A=64°, 求∠EDF的度数.
图2-Z-22
考点:平行线的性质.
考情:主要考查利用两直线平行的性质求角的度数或角之间的关系.
策略:由两直线平行可得同位角相等、内错角相等、同旁内角互补, 从而将直线的位置关系转化为角的数量关系.
链接4 [天水中考]将一把直尺和一块三角尺ABC(含30°, 60°角)如图2-Z-23所示摆放, 直尺一边与三角尺的两直角边分别交于点D, E, 另一边与三角尺的两直角边分别交于点F, A, 且∠CED=50°, 那么∠BFA的大小为( ).
A.145° B.140°
C.135° D.130°
B
图2-Z-23
分析 因为∠CDE=180°-∠C-∠CED=40°,DE∥AF,
所以∠CFA=∠CDE=40°,
所以∠BFA=180°-∠CFA=140°.
故选B.
谢 谢 观 看!
章末复习
第二章 相交线与平行线
章末复习
知识框架
归纳整合
素养提升
中考链接
知识框架
相交线
相交线与
平行线
平行线
尺规作图
相交
垂直
两条直线被第
三条直线所截
平行公理
判定
性质
定义
对顶角
补角
余角
相交
定义
性质:对顶角相等
定义
性质:同角或等角的补角相等
定义
性质:同角或等角的余角相等
平面内, 过一点有且只有一条直线与已知直线垂直
直线外一点与直线上各点连接的所有线段中, 垂线段最短
点到直线的距离
定义
垂直
两条直线被第
三条直线所截
同位角、内错角、同旁内角
简称“三线八角”
平行公理
公理:过直线外一点
有且只有一条直线与
这条直线平行
推论:平行于同一条
直线的两条直线平行
(1)同位角相等, 两直线平行
(2)内错角相等, 两直线平行
(3)同旁内角互补, 两直线平行
判定
(1)两直线平行, 同位角相等
(2)两直线平行, 内错角相等
(3)两直线平行, 同旁内角互补
性质
【要点指导】两条直线相交形成四个角, 这四个角中有两对对顶角、四对邻补角;当相交的两条直线互相垂直时, 相交形成的角是直角. 根据对顶角、邻补角之间的数量关系以及直角的定义, 可进行角度的相关计算.
归纳整合
专题一 两条直线相交构成的角的相关计算
例1 如图2-Z-1, 直线AB与直线CD相交于点O, 已知OE⊥AB于点O, ∠BOD=45°, 则∠COE的度数是( ).
A.125° B.135°
C.145° D.155°
B
图2-Z-1
相关题1 如图2-Z-2, AB与CD相交于点O, OE⊥CD于点O, ∠BOE=54°, 则∠AOC= °.
36
图2-Z-2
[解析] 因为OE⊥CD,∠BOE=54°,
所以∠BOD=90°-∠BOE=90°-54°=36°.
又因为∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=36°.
【要点指导】直线外一点到这条直线的垂线段的长度叫作点到直线的距离, 这说明, 点到直线的距离可以转化为两点之间的距离.
专题二 关于两点之间、点与直线之间的距离
例2 如图2-Z-3所示, AB∥CD, DE⊥AB于点E, 经测量知AD=BC
=1.6 cm, DE=1.4 cm.
(1)BC的长表示什么之间的距离?
(2)点D到直线AB的距离是1.4 cm
还是1.6 cm?为什么?
图2-Z-3
解: (1)BC的长表示点B与点C之间的距离.
(2)点D到直线AB的距离是1.4 cm.
理由:
因为DE⊥AB ,
所以DE是点D到直线AB的垂线段,
所以点D到直线AB的距离是1.4 cm.
相关题2 如图2-Z-4, 已知长方形ABCD.
(1)点A与点C之间的距离是指线段 的长;
(2)点D到线段AB的距离是指线段 的长.
图2-Z-4
解: (1)AC (2)AD
例3 如图2-Z-5, 已知点A, B以及直线l.
(1)请画出从点A到直线l的最短路线, 并写出其依据;
(2)请在直线l上确定一点O, 使点O到点A, B的距离之和最短, 并写出其依据.
图2-Z-5
解: (1)如图2-Z-5所示, AE为点A到直线l的最短路线.
依据:直线外一点与直线上各点连接的所有线段中, 垂线段最短.
(2)如图2-Z-5所示, 连接AB, AB与直线l的交点O即为所求.
依据:两点之间, 线段最短.
图2-Z-5
相关题3 如图2-Z-6, 在三角形ABC中, ∠BCA=90°,BC=3, AC=4, AB=5, P是线段AB上的一个动点,求线段CP的最小值.
图2-Z-6
【要点指导】综合利用题目中角的数量关系判定两直线平行, 再根据平行线的性质得出另外一对相等或互补的角, 从而进行相关的计算或说理;或先通过平行线得出角的相等或互补关系, 再根据平行线的判定得出另一组直线互相平行.
专题三 与平行线性质、判定有关的计算与说理题
例4 已知:如图2-Z-7, AB∥CD, BD平分∠ABC, CE平分∠DCF, ∠ACE=90°.
(1)判断BD和CE的位置关系, 并说明理由;
(2)判断AC和BD是否垂直, 并说明理由.
图2-Z-7
解:(1)BD∥CE.
理由:因为AB∥CD, 所以∠ABC=∠DCF.
因为BD平分∠ABC, CE平分∠DCF,
所以∠2= ∠ABC, ∠4= ∠DCF,
所以∠2=∠4,所以BD∥CE(同位角相等, 两直线平行).
(2)AC⊥BD.
理由:因为BD∥CE, 所以∠DGC+∠ACE=180°.
因为∠ACE=90°, 所以∠DGC=180°-90°=90°,即AC⊥BD.
相关题4 如图2-Z-8, DE⊥AB,EF⊥BC, 垂足分别为E,F, 若∠B=∠ADE, 则AD与EF平行吗?若平行,请说明理由.
图2-Z-8
[解析] 因为已知EF⊥BC,
所以只需说明AD⊥BC即可证明AD∥EF.
而根据条件可说明∠BDE+∠ADE=90°,
则可得AD⊥BC.
解:AD∥EF.
理由:
因为DE⊥AB,所以∠BED=90°,所以∠B+∠BDE=90°.因为∠B=∠ADE,
所以∠BDE+∠ADE=90°,即∠ADB=90°,所以AD⊥BC.
所以∠EFD=∠ADC=90°,
所以AD∥EF.
【要点指导】垂直是特殊的相交, 在数学图形中, 平行和垂直经常同时出现, 解决问题时既要注意从线角关系的角度转化问题、推导出结论, 还要注意从线线关系的角度发现结论、转化问题, 多角度思考问题.
专题四 平行与垂直的综合运用
例5 如图2-Z-9, 已知AD⊥BC于点D, EG⊥BC于点G, ∠E=∠1, AD平分∠BAC吗?试说明理由.
图2-Z-9
解:AD平分∠BAC. 理由:如图2-Z-9,
因为AD⊥BC于点D, EG⊥BC于点G(已知),
所以∠ADC=∠EGC=90°(垂直的定义),
所以AD∥EG(同位角相等, 两直线平行),
所以∠1=∠2(两直线平行, 内错角相等),
∠E=∠3(两直线平行, 同位角相等).
又因为∠E=∠1(已知), 所以∠2=∠3(等量代换),
所以AD平分∠BAC(角平分线的定义).
图2-Z-9
相关题5 已知:如图2-Z-10,AB∥CD, OE平分∠AOD,OF⊥OE 于点O, ∠D=60°, 求∠BOF的度数.
图2-Z-10
解:因为AB∥CD,∠D=60°,
所以∠AOD=180°-∠D=180°-60°=120°,
∠BOD=∠D=60°.
因为OE平分∠AOD,
所以∠EOD=120°÷2=60°.
因为OF⊥OE于点O,所以∠EOF=90°,
所以∠DOF=90°-60°=30°,
所以∠BOF=∠BOD-∠DOF=60°-30°=30°.
【要点指导】在几何题中, 有些题目未给出图形, 这时我们就要结合题意先画出图形, 再解决问题. 这一过程常常具有多种符合题意的图形, 需要我们分类讨论解决.
素养提升
专题一 分类讨论思想
例1 已知一个角的两边与另一个角的两边分别平行, 则这两个角的数量关系为 .
相等或互补
分析 设两个角分别为∠1, ∠2, 根据题目信息可得有以下两种情况(图形画法不唯一):
由图2-Z-11可知∠1=∠2或∠1+∠2=180°,
即这两个角的数量关系为相等或互补.
图2-Z-11
相关题1 已知:∠BOC 在∠AOB的外部, OE平分∠AOB,OF平分∠BOC, OD平分∠AOC, ∠AOE=30°, ∠ B O D = 2 0 °, 试 求
∠COF的度数.
[解析]本题没有给出具体的图形, ∠AOB既可大于∠BOC,
又可小于∠BOC, 则应分这两种情况分别求解.
图①
图②
【要点指导】由本章的学习, 应该对转化这一数学思想有更深刻的体会. 这一思想在平行线与角的关系中表现特别明显.当我们要说明两条直线平行时, 经常把问题转化为说明两角相等或互补;当我们说明两角之间的数量关系时, 又经常将其转化为说明两直线平行.在几何推理中, 经常通过转化已知条件推出要求的结论, 必要时还需要添加辅助线进行转化.
专题二 转化思想
例2 [新乡长垣县期中] 如图2-Z-12①, E是直线AB, CD之间的一点,
AB∥CD, 连接EA, ED.
(1)探究猜想:
①若∠EAB=30°, ∠EDC=40°,
求∠AED的度数;
②若∠EAB=20°, ∠EDC=60°,
求∠AED的度数;
③猜想图①中∠AED, ∠EAB, ∠EDC之间的数量关系, 并说明理由.
图2-Z-12
(2)扩展应用:
如图②, 射线FE与长方形ABCD的边AB交于点E, 与边CD交于点F,
①②③④分别是被射线FE隔开的4个
区域(不含边界, 其中区域③④位于直
线AB的上方), P是位于以上四个区域
内的一点, 试猜∠PEB, ∠PFC, ∠EPF
之间的数量关系(不要求说明理由).
图2-Z-12
分析 (1)①过点E作EF∥AB, 再由平行线的性质即可得出结论;②, ③题根据①中的方法即可得出结论.
(2)当点P分别位于①, ②, ③, ④四个区域内时, 分别根据平行线的性质进行求解即可得出结论.
解:(1)如图2-Z-13①, 过点E作EF∥AB,
因为AB∥CD, 所以CD∥EF.
因为∠EAB=30°, ∠EDC=40°,
所以∠1=∠EAB=30°, ∠2=∠EDC=40°,
所以∠AED=∠1+∠2=70°.
图2-Z-13
②如图①, 过点E作EF∥AB,
因为AB∥CD,所以CD∥EF.
因为∠EAB=20°, ∠EDC=60°,
所以∠1=∠EAB=20°, ∠2=∠EDC=60°,
所以∠AED=∠1+∠2=80°.
图2-Z-13
③猜想:∠AED=∠EAB+∠EDC.
理由:如图①, 过点E作EF∥AB,
因为AB∥CD, 所以EF∥CD
(平行于同一条直线的两直线平行),
所以∠1=∠EAB, ∠2=∠EDC
(两直线平行, 内错角相等),
所以∠AED=∠1+∠2=∠EAB+∠EDC(等量代换).
图2-Z-13
(2)当点P在区域①内时, 如图②, ∠EPF=360°-(∠PEB+∠PFC);
当点P在区域②内时, 如图③, ∠EPF=∠PEB+∠PFC;
当点P在区域③内时, 如图④, ∠EPF=∠PEB-∠PFC;
当点P在区域④内时, 如图⑤, ∠EPF=∠PFC-∠PEB.
图2-Z-13
相关题2-1 [深圳龙岗区期末] 如图2-Z-14, 已知AB∥CD,BE平分∠ABC, DE平分∠ADC, ∠BAD=80°.
(1)求∠EDC的度数;
(2)若∠BCD=n°, 试求∠BED的度数(用含n的式子表示).
图2-Z-14
相关题2-2 [湘潭中考] 如图2-Z-15,E是AD延长线上一点,如果添加一个条件, 使BC∥AD, 则可添加的条件为 __________________
_________________________________________________________
. (任意添加一个符合题意的条件即可)
图2-Z-15
∠A+∠ABC=180°
或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE (答
案不唯一)
[解析]若∠A+∠ABC=180°,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD.
中考链接
母题1 (教材P40习题2.1第1题)
如图2-Z-16, 直线a, b相交, ∠1=38°, 求∠2,∠3, ∠4的度数.
图2-Z-16
考点:角的计算.
考情:一般以选择题、填空题的形式考查, 常考查计算某一个角的度数.
策略:对顶角的性质常与余角、补角结合在一起考查. 牢记性质:对顶角相等, 互补两角的和为180°, 互余两角的和为90°.
链接1 [泉州中考]如图2-Z-17, 直线AB与CD相交于点O. 若∠AOD=50°, 则∠BOC= °.
50
图2-Z-17
分析 因为∠BOC与∠AOD是对顶角,
所以∠BOC=∠AOD=50°.
母题2 (教材P43习题2.2第3题)
如图2-Z-18, 要把水渠中的水引到C点, 在渠岸AB的什么地方开沟, 才能使沟最短?画出图形, 并说明理由.
图2-Z-18
考点:点到直线的距离、垂线段最短.
考情:一般在选择题或者几何最值计算问题中考查.
策略:明确点到直线的距离是指垂线段的长度.
链接2 [厦门中考]如图2-Z-19, 三角形ABC是锐角三角形, 过点C作CD⊥AB, 垂足为D, 则点C到直线AB的距离是( ).
A.线段CA的长
B.线段CD的长
C.线段AD的长
D.线段AB的长
B
图2-Z-19
母题3 (教材P49习题2.4第2题)
如图2-Z-20 ,∠DAB+∠CDA=180°,∠ABC=∠1, 直线AB与CD平行吗?直线AD与BC呢?为什么?
图2-Z-20
考点:判定两直线平行的条件.
考情:主要考查两直线平行的判定,常在选择题中出现, 有时也作为解答题的一小问出现.
策略:根据两直线平行的判定方法:同位角相等, 两直线平行;内错角相等, 两直线平行;同旁内角互补, 两直线平行, 从而将角的数量关系转化为直线的位置关系.
链接3 [郴州中考]如图2-Z-21, 直线a, b被直线c所截, 下列条件中, 不能判定a∥b的是( ).
A.∠2=∠4 B.∠1+∠4=180°
C.∠5=∠4 D.∠1=∠3
D
分析 由∠2=∠4或∠1+∠4=180°
或∠5=∠4, 可得a∥b;
由∠1=∠3, 不能得到a∥b.
故选D.
图2-Z-21
母题4 (教材P54习题2.6第4题)
如图2-Z-22, AC∥ED,AB∥FD, ∠A=64°, 求∠EDF的度数.
图2-Z-22
考点:平行线的性质.
考情:主要考查利用两直线平行的性质求角的度数或角之间的关系.
策略:由两直线平行可得同位角相等、内错角相等、同旁内角互补, 从而将直线的位置关系转化为角的数量关系.
链接4 [天水中考]将一把直尺和一块三角尺ABC(含30°, 60°角)如图2-Z-23所示摆放, 直尺一边与三角尺的两直角边分别交于点D, E, 另一边与三角尺的两直角边分别交于点F, A, 且∠CED=50°, 那么∠BFA的大小为( ).
A.145° B.140°
C.135° D.130°
B
图2-Z-23
分析 因为∠CDE=180°-∠C-∠CED=40°,DE∥AF,
所以∠CFA=∠CDE=40°,
所以∠BFA=180°-∠CFA=140°.
故选B.
谢 谢 观 看!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
