周末阶段复习提升训练卷2(9.1图形的旋转-9.4特殊平行四边形)-2020-2021学年苏科版八年级数学下册(含答案)
文档属性
| 名称 | 周末阶段复习提升训练卷2(9.1图形的旋转-9.4特殊平行四边形)-2020-2021学年苏科版八年级数学下册(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览


文档简介
周末阶段复习提升训练卷2(9.1图形的旋转-9.4特殊平行四边形)
-20-21苏科版八年级数学下册
一、选择题
1、如图,点A、B、C、D、O都在方格纸的格点上,若△CDO是由△ABO绕点O按顺时针方向旋转而得,则旋转的角度是( )
A.30° B.45° C.60° D.90°
(5) (6)
2、下列图形中既是轴对称图形,又是中心对称图形的是( )
A.B. C.D.
3、平行四边形一边的长是,则这个平行四边形的两条对角线长可以是( )
A.或 B.或 C.或 D.或
4、已知菱形,对角线,,则菱形的面积为( )
A. 60 B. 50 C. 40 D. 30
5、如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
6、如图,下列条件中①②③④,能使平行四边形是菱形的是( )
A. ①③ B. ②③ C. ③④ D. ①②③
7、已知下列命题:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
8、下列说法正确的有( )
①两条对角线相等的四边形是矩形;②有一组对边相等,一组对角是直角的四边形是矩形;
③一个角为直角,两条对角线相等的四边形是矩形;④四个角都相等的四边形是矩形;
⑤对角线相等且垂直的四边形是矩形;⑥有一个角是直角的平行四边形是矩形.
A. 1个 B. 2个 C. 3个 D. 4个
9、如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列条件
①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF是菱形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
(10) (11)
10、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD = ,④ 中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题
11、如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
则∠A的度数是 .
12、给出如下5种图形:①矩形,②等边三角形,③正五边形,④圆,⑤线段.其中,是轴对称图形但不是中心对称图形的有 .(请将所有符合题意的序号填在横线上)
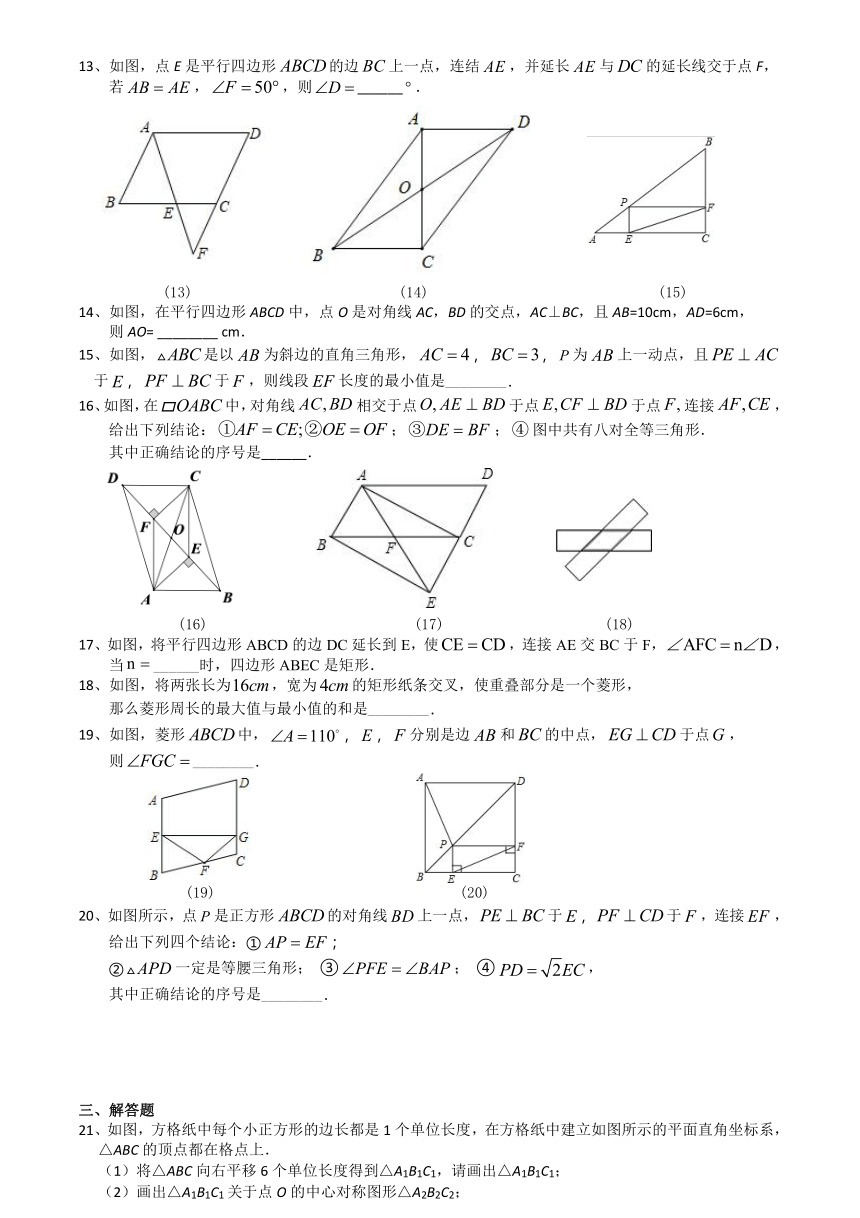
13、如图,点E是平行四边形的边上一点,连结,并延长与的延长线交于点F,若,,则______.
(14) (15)
14、如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,AC⊥BC,且AB=10cm,AD=6cm,
则AO= ________ cm.
15、如图,是以为斜边的直角三角形,,,为上一动点,且 于,于,则线段长度的最小值是________.
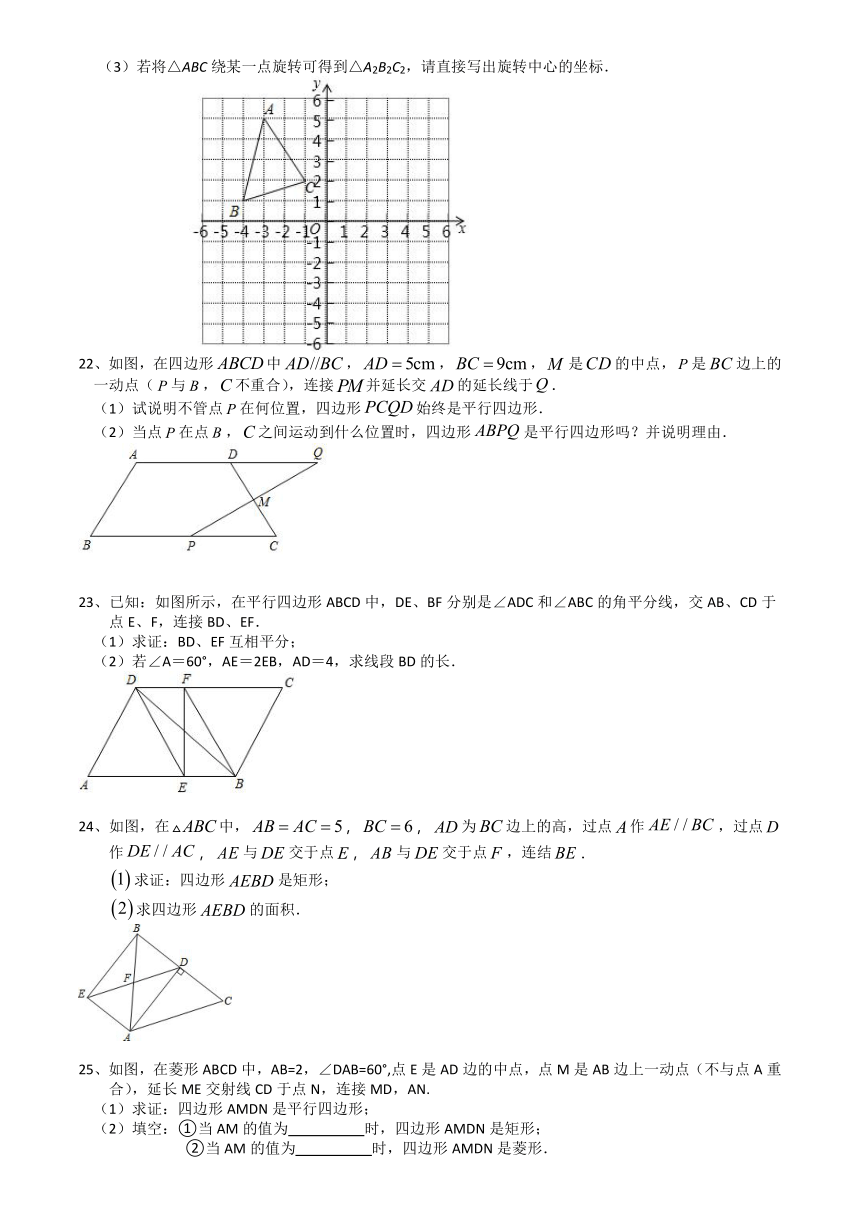
16、如图,在中,对角线相交于点于点于点连接,给出下列结论:;;图中共有八对全等三角形.
其中正确结论的序号是______.
(17) (18)
17、如图,将平行四边形ABCD的边DC延长到E,使,连接AE交BC于F,,当______时,四边形ABEC是矩形.
18、如图,将两张长为,宽为的矩形纸条交叉,使重叠部分是一个菱形,
那么菱形周长的最大值与最小值的和是________.
19、如图,菱形中,,,分别是边和的中点,于点,
则________.
(20)
20、如图所示,点是正方形的对角线上一点,于,于,连接,给出下列四个结论:①;?
②一定是等腰三角形;??③;??④,
其中正确结论的序号是________.
三、解答题
21、如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
22、如图,在四边形中,,,是的中点,是边上的一动点(与,不重合),连接并延长交的延长线于.
(1)试说明不管点在何位置,四边形始终是平行四边形.
(2)当点在点,之间运动到什么位置时,四边形是平行四边形吗?并说明理由.
23、已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
24、如图,在中,,,为边上的高,过点作,过点作,与交于点,与交于点,连结.
求证:四边形是矩形;
求四边形的面积.
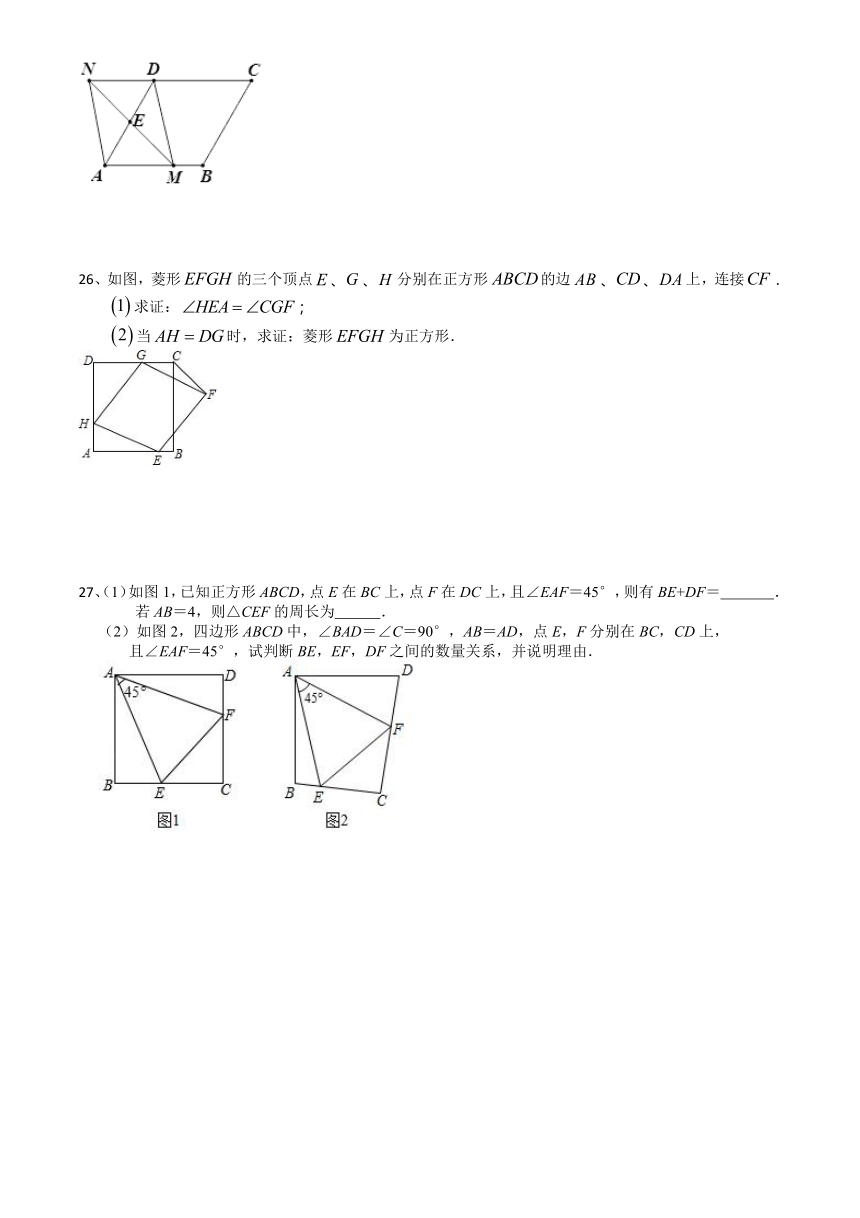
25、如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
26、如图,菱形的三个顶点、、分别在正方形的边、、上,连接.
求证:;
当时,求证:菱形为正方形.
27、(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF= .
若AB=4,则△CEF的周长为 .
(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,
且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
周末阶段复习提升训练卷2(9.1图形的旋转-9.4特殊平行四边形)
-20-21苏科版八年级数学下册(答案)
一、选择题
1、如图,点A、B、C、D、O都在方格纸的格点上,若△CDO是由△ABO绕点O按顺时针方向旋转而得,则旋转的角度是( )
A.30° B.45° C.60° D.90°
【解析】观察图象可知,∠AOC=∠BOD=90°,
∴旋转角为90°,
故选:D.
2、下列图形中既是轴对称图形,又是中心对称图形的是( )
A.B. C.D.
【解析】A、既是轴对称图形,又是中心对称图形,故本选项符合题意;
B、是轴对称图形,不是中心对称图形,故本选项不符合题意;
C、是轴对称图形,不是中心对称图形,故本选项不符合题意;
D、是轴对称图形,不是中心对称图形,故本选项不符合题意;
故选:A.
3、平行四边形一边的长是,则这个平行四边形的两条对角线长可以是( )
A.或 B.或 C.或 D.或
解:∵四边形ABCD是平行四边形,∴OA=AC,OB=BD,
A、∵AC=4cm,BD=6cm,∴OA=2cm,OB=3cm,∴OA+OB=5cm<12cm,不能组成三角形,故不符合;
B、∵AC=6cm,BD=10cm,∴OA=3cm,OB=5cm,∴OA+OB=8cm<12cm,不能组成三角形,故不符合;
C、∵AC=12cm,BD=12cm,∴OA=6cm,OB=6cm,∴OA+OB=12cm=12cm,
不能组成三角形,故不符合;
D、∵AC=12cm,BD=14cm,∴OA=6cm,OB=7cm,∴OA+OB=13cm>12cm,能组成三角形,故符合;
故选D.
4、已知菱形,对角线,,则菱形的面积为( )
A. 60 B. 50 C. 40 D. 30
【详解】∵菱形ABCD,对角线AC=5,BD=12,
∴S菱形ABCD=?AC?BD=×5×12=30, 故选D.
5、如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
解:A、∵,∴AO=CO,
由于四边形ABCD是平行四边形,则BO=DO,∴四边形DEBF是平行四边形;
B、不能证明四边形DEBF是平行四边形;
C、∵四边形ABCD是平行四边形,∴AD=BC,∠DAE=∠BCF,又∠ADE=∠CBF,
∴△DAE≌△BCF(ASA),∴AE=CF,同A可证四边形DEBF是平行四边形;
D、同C可证:△ABE≌△CDF(ASA),∴AE=CF,同A可证四边形DEBF是平行四边形;
故选:B.
6、如图,下列条件中①②③④,能使平行四边形是菱形的是( )
A. ①③ B. ②③ C. ③④ D. ①②③
【详解】①?ABCD中,AC⊥BD,根据对角线互相垂直的平行四边形是菱形,即可判定?ABCD是菱形;
故①正确;
②?ABCD中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,即可判定?ABCD是矩形,而不能判定?ABCD是菱形;故②错误;
③?ABCD中,AB=BC,根据一组邻边相等的平行四边形是菱形,即可判定?ABCD是菱形;故③正确;
D、?ABCD中,AC=BD,根据对角线相等的平行四边形是矩形,即可判定?ABCD是矩形,而不能判定?ABCD是菱形;故④错误.
故选A.
7、已知下列命题:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
8、下列说法正确的有( )
①两条对角线相等的四边形是矩形;②有一组对边相等,一组对角是直角的四边形是矩形;
③一个角为直角,两条对角线相等的四边形是矩形;④四个角都相等的四边形是矩形;
⑤对角线相等且垂直的四边形是矩形;⑥有一个角是直角的平行四边形是矩形.
A. 1个 B. 2个 C. 3个 D. 4个
【详解】两条对角线相等且相互平分的四边形为矩形.①③⑤错.
有一个角为直角的平行四边形为矩形.②④⑥正确.
故选C.
9、如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列条件
①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF是菱形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
【详解】解:如图,连接BD,交AC于点O,
在正方形ABCD中,AB=BC,∠BAC=∠ACB,AC⊥BD,AO=CO,BO=DO,
①在△ABE与△BCF中,,∴△ABE≌△BCF(ASA),∴BE=BF,
∵AC⊥BD,∴OE=OF,所以四边形BEDF是菱形,故①选项正确;
②正方形ABCD中,AC=BD,∴OA=OB=OC=OD,
∵AE=CF,∴OE=OF,又EF⊥BD,BO=OD,∴四边形BEDF是菱形,故②选项正确;
③AB=AF,不能推出四边形BEDF其它边的关系,故不能判定是菱形,本选项错误;
④BE=BF,同①的后半部分证明,故④选项正确.
所以①②④共3个可以判定四边形BEDF是菱形. 故选:C.
10、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD = ,④ 中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【详解】∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°.
∵AE=BF=1,∴BE=CF=4-1=3.
在△EBC和△FCD中,∵BC=CD,∠B=∠DCF,BE=CF,∴△EBC≌△FCD(SAS).
∴∠CFD=∠BEC.∴∠BCE+∠BEC=∠BCE+∠CFD=90°.∴∠DOC=90°.故①正确.
如图,连接DE,若OC=OE,∵DF⊥EC,∴CD=DE.
∵CD=AD<DE(矛盾),故②错误.
∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC.
∴tan∠OCD=tan∠DFC=.故③正确.
∵△EBC≌△FCD,∴S△EBC=S△FCD.
∴S△EBC-S△FOC=S△FCD-S△FOC,即S△ODC=S四边形BEOF.故④正确.故选C.
二、填空题
11、如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
则∠A的度数是 .
【解析】∵△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
∴∠AOC=∠BOD=40°,OA=OC,
∵OA=OC,∴∠A=∠OCA,∴∠A(180°﹣40°)=70°,
故答案为:70°.
12、给出如下5种图形:①矩形,②等边三角形,③正五边形,④圆,⑤线段.其中,是轴对称图形但不是中心对称图形的有 .(请将所有符合题意的序号填在横线上)
【解析】①矩形是轴对称图形,是中心对称图形;
②等边三角形是轴对称图形,不是中心对称图形;
③正五边形是轴对称图形,不是中心对称图形;
④圆是轴对称图形,是中心对称图形;
⑤线段是轴对称图形,是中心对称图形;
则是轴对称图形但不是中心对称图形的②③,
故答案为:②③.
13、如图,点E是平行四边形的边上一点,连结,并延长与的延长线交于点F,若,,则______.
解:如图所示,
∵四边形ABCD是平行四边形,∴AB∥DC,∴∠F=∠BAE=50°,.
∵AB=AE,∴∠B=∠AEB=65°,∴∠D=∠B=65°.故答案是:65.
14、如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,AC⊥BC,且AB=10cm,AD=6cm,
则AO= ________ cm.
解:在中,BC=AD=6cm, AO=CO,
∵AC⊥BC,,∴, ∴
故答案为:4.
15、如图,是以为斜边的直角三角形,,,为上一动点,且 于,于,则线段长度的最小值是________.
【详解】连接PC,∵PE⊥AC,PF⊥BC,∴∠PEC=∠PFC=∠C=90°;
又∵∠ACB=90°,∴四边形ECFP是矩形,∴EF=PC,∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=4,BC=3,∴AB=5,
∴AC?BC=AB?PC,∴PC=.∴线段EF长的最小值为;
故答案是:.
16、如图,在中,对角线相交于点于点于点连接,给出下列结论:;;图中共有八对全等三角形.
其中正确结论的序号是______.
解:在中,
,,,
于点,于点,,
,四边形是平行四边形, ,故①②正确,
,,即,故③正确,
∵,和是中心对称图形,点是对称中心,
易证 ,
,
,
∴共10对全等三角形,故④错误;
故答案为:①②③
17、如图,将平行四边形ABCD的边DC延长到E,使,连接AE交BC于F,,当______时,四边形ABEC是矩形.
【详解】解:当∠AFC=2∠D时,四边形ABEC是矩形.
∵四边形ABCD是平行四边形,∴BC∥AD,∠BCE=∠D,
由题意易得AB∥EC,AB∥EC,∴四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,∴四边形ABEC是矩形,故答案为2.
18、如图,将两张长为,宽为的矩形纸条交叉,使重叠部分是一个菱形,
那么菱形周长的最大值与最小值的和是________.
【详解】当两张纸条如图1所示放置时,菱形周长最大,
设这时菱形的边长为xcm,由勾股定理:x2=(16?x)2+42,得:2x=17,
∴4x=34,即菱形的最大周长为34cm;
当两张纸条如图所2示放置时,即是正方形时取得最小值为:4×4=16.
∴菱形周长的最大值与最小值的和是34+16=50,
故答案为50.
19、如图,菱形中,,,分别是边和的中点,于点,
则________.
【详解】延长GF,交AB的延长线于点P,∵F为BC的中点,∴BF=CF,
∵四边形ABCD为菱形,∴AB∥DC,∴∠PBF=∠GCF,∠BFP=∠CFG,
在△BPF与△CGF中,,∴△BPF≌△CGF,∴GF=PF,∴F为PG中点.
又∵由题可知,∠BEG=90°,∴EF=12PG,
∵GF=12PG,∴EF=GF,∴∠FEG=∠EGF,
∵∠BEG=∠EGC=90°,∴∠BEG?∠FEG=∠EGC?∠EGF,即∠BEF=∠FGC,
∵四边形ABCD为菱形,∴AB=BC,∠ABC=180°?∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=(180°?70°)=55°,∴∠FGC=55°.
故答案为:55°.
20、如图所示,点是正方形的对角线上一点,于,于,连接,给出下列四个结论:①;?
②一定是等腰三角形;??③;??④,
其中正确结论的序号是________.
【详解】解:如图,连接PC,
在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
∵在△ABP和△CBP中,∴△ABP≌△CBP(SAS),∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,∴四边形PECF是矩形,∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
∵PF⊥CD,∠BDC=45°,∴△PDF是等腰直角三角形,∴PD=PF,
又∵矩形的对边PF=EC,∴PD=EC,故④正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
综上所述,正确的结论有①③④.
故答案为①③④.
三、解答题
21、如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
【解析】(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)根据图形可知:旋转中心的坐标为:(﹣3,0).
22、如图,在四边形中,,,是的中点,是边上的一动点(与,不重合),连接并延长交的延长线于.
(1)试说明不管点在何位置,四边形始终是平行四边形.
(2)当点在点,之间运动到什么位置时,四边形是平行四边形吗?并说明理由.
解:(1)∵AD∥BC,∴∠QDM=∠PCM,
∵M是CD的中点,∴DM=CM,
∵∠DMQ=∠CMP,DM=CM,∠QDM=∠PCM,∴△PCM≌△QDM(ASA).∴DQ=PC,
∵AD∥BC,∴四边形PCQD是平行四边形,
∴不管点P在何位置,四边形PCQD始终是平行四边形;
(2)当四边形ABPQ是平行四边形时,PB=AQ,
∵BC-CP=AD+QD,∴9-CP=5+CP,∴CP=(9-5)÷2=2.
∴当PC=2时,四边形ABPQ是平行四边形.
23、已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
【详解】(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,∴AE=AD,CF=CB,∴AE=CF,
∴AB-AE=CD-CF,即BE=DF,
∵DF∥BE,∴四边形DEBF是平行四边形,∴BD、EF互相平分;
(2)如图,过D点作DG⊥AB于点G,
∵∠A=,AE=AD,∴△ADE是等边三角形,
∵AD=4,∴DE=AE=4,
∵AE=2EB,∴BE=2,
在Rt△ADG中,AD=4,∠A=,∴,∴DG=,
∴.
24、如图,在中,,,为边上的高,过点作,过点作,与交于点,与交于点,连结.
求证:四边形是矩形;
求四边形的面积.
【详解】∵,,∴四边形是平行四边形.∴.
在中,,为边上的高,∴,.
∴.∴四边形是矩形.
在中,,,,
∴.∴四边形的面积.
25、如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
试题解析:(1)证明:∵四边形ABCD是菱形,∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点, ∴DE=AE,∴△NDE≌△MAE,
∴ND=MA,∴四边形AMDN是平行四边形;
(2)解:①当AM的值为1时,四边形AMDN是矩形.理由如下:
∵AM=1=AD,∴∠ADM=30°
∵∠DAM=60°,∴∠AMD=90°,∴平行四边形AMDN是矩形;
②当AM的值为2时,四边形AMDN是菱形.理由如下:
∵AM=2,∴AM=AD=2,∴△AMD是等边三角形,∴AM=DM,
∴平行四边形AMDN是菱形,
26、如图,菱形的三个顶点、、分别在正方形的边、、上,连接.
求证:;
当时,求证:菱形为正方形.
【详解】(1)连接,∵,∴,
∵,∴,∴;
∵四边形是正方形,∴,
∵四边形是菱形,∴,
在和中,,∴,
∴, 又∵,
∴,∴,∴菱形为正方形;
27、(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF= .若AB=4,则△CEF的周长为 .
(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
【答案】解:(1)延长EB至H,使BH=DF,连接AH,如图1,
∵在正方形ABCD中,∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,,∴△ADF≌△ABH(SAS),∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,,∴△FAE≌△HAE(SAS),∴EF=HE=BE+HB,
∴EF=BE+DF,∴△CEF的周长=EF+CE+CF=BE+CE+DF+CF=BC+CD=2AB=8.
故答案为:EF;8.
(2)EF=BE+DF,理由如下:
延长CB至M,使BM=DF,连接AM,如图2,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,∴∠D=∠ABM,
在△ABM和△ADF中,,∴△ABM≌△ADF(SAS),∴AF=AM,∠DAF=∠BAM,
∵∠BAD=∠C=90°,∠EAF=45°,即∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,,∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,即EF=BE+DF.
-20-21苏科版八年级数学下册
一、选择题
1、如图,点A、B、C、D、O都在方格纸的格点上,若△CDO是由△ABO绕点O按顺时针方向旋转而得,则旋转的角度是( )
A.30° B.45° C.60° D.90°
(5) (6)
2、下列图形中既是轴对称图形,又是中心对称图形的是( )
A.B. C.D.
3、平行四边形一边的长是,则这个平行四边形的两条对角线长可以是( )
A.或 B.或 C.或 D.或
4、已知菱形,对角线,,则菱形的面积为( )
A. 60 B. 50 C. 40 D. 30
5、如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
6、如图,下列条件中①②③④,能使平行四边形是菱形的是( )
A. ①③ B. ②③ C. ③④ D. ①②③
7、已知下列命题:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
8、下列说法正确的有( )
①两条对角线相等的四边形是矩形;②有一组对边相等,一组对角是直角的四边形是矩形;
③一个角为直角,两条对角线相等的四边形是矩形;④四个角都相等的四边形是矩形;
⑤对角线相等且垂直的四边形是矩形;⑥有一个角是直角的平行四边形是矩形.
A. 1个 B. 2个 C. 3个 D. 4个
9、如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列条件
①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF是菱形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
(10) (11)
10、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD = ,④ 中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题
11、如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
则∠A的度数是 .
12、给出如下5种图形:①矩形,②等边三角形,③正五边形,④圆,⑤线段.其中,是轴对称图形但不是中心对称图形的有 .(请将所有符合题意的序号填在横线上)
13、如图,点E是平行四边形的边上一点,连结,并延长与的延长线交于点F,若,,则______.
(14) (15)
14、如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,AC⊥BC,且AB=10cm,AD=6cm,
则AO= ________ cm.
15、如图,是以为斜边的直角三角形,,,为上一动点,且 于,于,则线段长度的最小值是________.
16、如图,在中,对角线相交于点于点于点连接,给出下列结论:;;图中共有八对全等三角形.
其中正确结论的序号是______.
(17) (18)
17、如图,将平行四边形ABCD的边DC延长到E,使,连接AE交BC于F,,当______时,四边形ABEC是矩形.
18、如图,将两张长为,宽为的矩形纸条交叉,使重叠部分是一个菱形,
那么菱形周长的最大值与最小值的和是________.
19、如图,菱形中,,,分别是边和的中点,于点,
则________.
(20)
20、如图所示,点是正方形的对角线上一点,于,于,连接,给出下列四个结论:①;?
②一定是等腰三角形;??③;??④,
其中正确结论的序号是________.
三、解答题
21、如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
22、如图,在四边形中,,,是的中点,是边上的一动点(与,不重合),连接并延长交的延长线于.
(1)试说明不管点在何位置,四边形始终是平行四边形.
(2)当点在点,之间运动到什么位置时,四边形是平行四边形吗?并说明理由.
23、已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
24、如图,在中,,,为边上的高,过点作,过点作,与交于点,与交于点,连结.
求证:四边形是矩形;
求四边形的面积.
25、如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
26、如图,菱形的三个顶点、、分别在正方形的边、、上,连接.
求证:;
当时,求证:菱形为正方形.
27、(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF= .
若AB=4,则△CEF的周长为 .
(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,
且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
周末阶段复习提升训练卷2(9.1图形的旋转-9.4特殊平行四边形)
-20-21苏科版八年级数学下册(答案)
一、选择题
1、如图,点A、B、C、D、O都在方格纸的格点上,若△CDO是由△ABO绕点O按顺时针方向旋转而得,则旋转的角度是( )
A.30° B.45° C.60° D.90°
【解析】观察图象可知,∠AOC=∠BOD=90°,
∴旋转角为90°,
故选:D.
2、下列图形中既是轴对称图形,又是中心对称图形的是( )
A.B. C.D.
【解析】A、既是轴对称图形,又是中心对称图形,故本选项符合题意;
B、是轴对称图形,不是中心对称图形,故本选项不符合题意;
C、是轴对称图形,不是中心对称图形,故本选项不符合题意;
D、是轴对称图形,不是中心对称图形,故本选项不符合题意;
故选:A.
3、平行四边形一边的长是,则这个平行四边形的两条对角线长可以是( )
A.或 B.或 C.或 D.或
解:∵四边形ABCD是平行四边形,∴OA=AC,OB=BD,
A、∵AC=4cm,BD=6cm,∴OA=2cm,OB=3cm,∴OA+OB=5cm<12cm,不能组成三角形,故不符合;
B、∵AC=6cm,BD=10cm,∴OA=3cm,OB=5cm,∴OA+OB=8cm<12cm,不能组成三角形,故不符合;
C、∵AC=12cm,BD=12cm,∴OA=6cm,OB=6cm,∴OA+OB=12cm=12cm,
不能组成三角形,故不符合;
D、∵AC=12cm,BD=14cm,∴OA=6cm,OB=7cm,∴OA+OB=13cm>12cm,能组成三角形,故符合;
故选D.
4、已知菱形,对角线,,则菱形的面积为( )
A. 60 B. 50 C. 40 D. 30
【详解】∵菱形ABCD,对角线AC=5,BD=12,
∴S菱形ABCD=?AC?BD=×5×12=30, 故选D.
5、如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
解:A、∵,∴AO=CO,
由于四边形ABCD是平行四边形,则BO=DO,∴四边形DEBF是平行四边形;
B、不能证明四边形DEBF是平行四边形;
C、∵四边形ABCD是平行四边形,∴AD=BC,∠DAE=∠BCF,又∠ADE=∠CBF,
∴△DAE≌△BCF(ASA),∴AE=CF,同A可证四边形DEBF是平行四边形;
D、同C可证:△ABE≌△CDF(ASA),∴AE=CF,同A可证四边形DEBF是平行四边形;
故选:B.
6、如图,下列条件中①②③④,能使平行四边形是菱形的是( )
A. ①③ B. ②③ C. ③④ D. ①②③
【详解】①?ABCD中,AC⊥BD,根据对角线互相垂直的平行四边形是菱形,即可判定?ABCD是菱形;
故①正确;
②?ABCD中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,即可判定?ABCD是矩形,而不能判定?ABCD是菱形;故②错误;
③?ABCD中,AB=BC,根据一组邻边相等的平行四边形是菱形,即可判定?ABCD是菱形;故③正确;
D、?ABCD中,AC=BD,根据对角线相等的平行四边形是矩形,即可判定?ABCD是矩形,而不能判定?ABCD是菱形;故④错误.
故选A.
7、已知下列命题:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
8、下列说法正确的有( )
①两条对角线相等的四边形是矩形;②有一组对边相等,一组对角是直角的四边形是矩形;
③一个角为直角,两条对角线相等的四边形是矩形;④四个角都相等的四边形是矩形;
⑤对角线相等且垂直的四边形是矩形;⑥有一个角是直角的平行四边形是矩形.
A. 1个 B. 2个 C. 3个 D. 4个
【详解】两条对角线相等且相互平分的四边形为矩形.①③⑤错.
有一个角为直角的平行四边形为矩形.②④⑥正确.
故选C.
9、如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列条件
①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF是菱形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
【详解】解:如图,连接BD,交AC于点O,
在正方形ABCD中,AB=BC,∠BAC=∠ACB,AC⊥BD,AO=CO,BO=DO,
①在△ABE与△BCF中,,∴△ABE≌△BCF(ASA),∴BE=BF,
∵AC⊥BD,∴OE=OF,所以四边形BEDF是菱形,故①选项正确;
②正方形ABCD中,AC=BD,∴OA=OB=OC=OD,
∵AE=CF,∴OE=OF,又EF⊥BD,BO=OD,∴四边形BEDF是菱形,故②选项正确;
③AB=AF,不能推出四边形BEDF其它边的关系,故不能判定是菱形,本选项错误;
④BE=BF,同①的后半部分证明,故④选项正确.
所以①②④共3个可以判定四边形BEDF是菱形. 故选:C.
10、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD = ,④ 中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【详解】∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°.
∵AE=BF=1,∴BE=CF=4-1=3.
在△EBC和△FCD中,∵BC=CD,∠B=∠DCF,BE=CF,∴△EBC≌△FCD(SAS).
∴∠CFD=∠BEC.∴∠BCE+∠BEC=∠BCE+∠CFD=90°.∴∠DOC=90°.故①正确.
如图,连接DE,若OC=OE,∵DF⊥EC,∴CD=DE.
∵CD=AD<DE(矛盾),故②错误.
∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC.
∴tan∠OCD=tan∠DFC=.故③正确.
∵△EBC≌△FCD,∴S△EBC=S△FCD.
∴S△EBC-S△FOC=S△FCD-S△FOC,即S△ODC=S四边形BEOF.故④正确.故选C.
二、填空题
11、如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
则∠A的度数是 .
【解析】∵△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
∴∠AOC=∠BOD=40°,OA=OC,
∵OA=OC,∴∠A=∠OCA,∴∠A(180°﹣40°)=70°,
故答案为:70°.
12、给出如下5种图形:①矩形,②等边三角形,③正五边形,④圆,⑤线段.其中,是轴对称图形但不是中心对称图形的有 .(请将所有符合题意的序号填在横线上)
【解析】①矩形是轴对称图形,是中心对称图形;
②等边三角形是轴对称图形,不是中心对称图形;
③正五边形是轴对称图形,不是中心对称图形;
④圆是轴对称图形,是中心对称图形;
⑤线段是轴对称图形,是中心对称图形;
则是轴对称图形但不是中心对称图形的②③,
故答案为:②③.
13、如图,点E是平行四边形的边上一点,连结,并延长与的延长线交于点F,若,,则______.
解:如图所示,
∵四边形ABCD是平行四边形,∴AB∥DC,∴∠F=∠BAE=50°,.
∵AB=AE,∴∠B=∠AEB=65°,∴∠D=∠B=65°.故答案是:65.
14、如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,AC⊥BC,且AB=10cm,AD=6cm,
则AO= ________ cm.
解:在中,BC=AD=6cm, AO=CO,
∵AC⊥BC,,∴, ∴
故答案为:4.
15、如图,是以为斜边的直角三角形,,,为上一动点,且 于,于,则线段长度的最小值是________.
【详解】连接PC,∵PE⊥AC,PF⊥BC,∴∠PEC=∠PFC=∠C=90°;
又∵∠ACB=90°,∴四边形ECFP是矩形,∴EF=PC,∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=4,BC=3,∴AB=5,
∴AC?BC=AB?PC,∴PC=.∴线段EF长的最小值为;
故答案是:.
16、如图,在中,对角线相交于点于点于点连接,给出下列结论:;;图中共有八对全等三角形.
其中正确结论的序号是______.
解:在中,
,,,
于点,于点,,
,四边形是平行四边形, ,故①②正确,
,,即,故③正确,
∵,和是中心对称图形,点是对称中心,
易证 ,
,
,
∴共10对全等三角形,故④错误;
故答案为:①②③
17、如图,将平行四边形ABCD的边DC延长到E,使,连接AE交BC于F,,当______时,四边形ABEC是矩形.
【详解】解:当∠AFC=2∠D时,四边形ABEC是矩形.
∵四边形ABCD是平行四边形,∴BC∥AD,∠BCE=∠D,
由题意易得AB∥EC,AB∥EC,∴四边形ABEC是平行四边形.
∵∠AFC=∠FEC+∠BCE,∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,∴四边形ABEC是矩形,故答案为2.
18、如图,将两张长为,宽为的矩形纸条交叉,使重叠部分是一个菱形,
那么菱形周长的最大值与最小值的和是________.
【详解】当两张纸条如图1所示放置时,菱形周长最大,
设这时菱形的边长为xcm,由勾股定理:x2=(16?x)2+42,得:2x=17,
∴4x=34,即菱形的最大周长为34cm;
当两张纸条如图所2示放置时,即是正方形时取得最小值为:4×4=16.
∴菱形周长的最大值与最小值的和是34+16=50,
故答案为50.
19、如图,菱形中,,,分别是边和的中点,于点,
则________.
【详解】延长GF,交AB的延长线于点P,∵F为BC的中点,∴BF=CF,
∵四边形ABCD为菱形,∴AB∥DC,∴∠PBF=∠GCF,∠BFP=∠CFG,
在△BPF与△CGF中,,∴△BPF≌△CGF,∴GF=PF,∴F为PG中点.
又∵由题可知,∠BEG=90°,∴EF=12PG,
∵GF=12PG,∴EF=GF,∴∠FEG=∠EGF,
∵∠BEG=∠EGC=90°,∴∠BEG?∠FEG=∠EGC?∠EGF,即∠BEF=∠FGC,
∵四边形ABCD为菱形,∴AB=BC,∠ABC=180°?∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=(180°?70°)=55°,∴∠FGC=55°.
故答案为:55°.
20、如图所示,点是正方形的对角线上一点,于,于,连接,给出下列四个结论:①;?
②一定是等腰三角形;??③;??④,
其中正确结论的序号是________.
【详解】解:如图,连接PC,
在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
∵在△ABP和△CBP中,∴△ABP≌△CBP(SAS),∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,∴四边形PECF是矩形,∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
∵PF⊥CD,∠BDC=45°,∴△PDF是等腰直角三角形,∴PD=PF,
又∵矩形的对边PF=EC,∴PD=EC,故④正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
综上所述,正确的结论有①③④.
故答案为①③④.
三、解答题
21、如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
【解析】(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)根据图形可知:旋转中心的坐标为:(﹣3,0).
22、如图,在四边形中,,,是的中点,是边上的一动点(与,不重合),连接并延长交的延长线于.
(1)试说明不管点在何位置,四边形始终是平行四边形.
(2)当点在点,之间运动到什么位置时,四边形是平行四边形吗?并说明理由.
解:(1)∵AD∥BC,∴∠QDM=∠PCM,
∵M是CD的中点,∴DM=CM,
∵∠DMQ=∠CMP,DM=CM,∠QDM=∠PCM,∴△PCM≌△QDM(ASA).∴DQ=PC,
∵AD∥BC,∴四边形PCQD是平行四边形,
∴不管点P在何位置,四边形PCQD始终是平行四边形;
(2)当四边形ABPQ是平行四边形时,PB=AQ,
∵BC-CP=AD+QD,∴9-CP=5+CP,∴CP=(9-5)÷2=2.
∴当PC=2时,四边形ABPQ是平行四边形.
23、已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
【详解】(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,∴AE=AD,CF=CB,∴AE=CF,
∴AB-AE=CD-CF,即BE=DF,
∵DF∥BE,∴四边形DEBF是平行四边形,∴BD、EF互相平分;
(2)如图,过D点作DG⊥AB于点G,
∵∠A=,AE=AD,∴△ADE是等边三角形,
∵AD=4,∴DE=AE=4,
∵AE=2EB,∴BE=2,
在Rt△ADG中,AD=4,∠A=,∴,∴DG=,
∴.
24、如图,在中,,,为边上的高,过点作,过点作,与交于点,与交于点,连结.
求证:四边形是矩形;
求四边形的面积.
【详解】∵,,∴四边形是平行四边形.∴.
在中,,为边上的高,∴,.
∴.∴四边形是矩形.
在中,,,,
∴.∴四边形的面积.
25、如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
试题解析:(1)证明:∵四边形ABCD是菱形,∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点, ∴DE=AE,∴△NDE≌△MAE,
∴ND=MA,∴四边形AMDN是平行四边形;
(2)解:①当AM的值为1时,四边形AMDN是矩形.理由如下:
∵AM=1=AD,∴∠ADM=30°
∵∠DAM=60°,∴∠AMD=90°,∴平行四边形AMDN是矩形;
②当AM的值为2时,四边形AMDN是菱形.理由如下:
∵AM=2,∴AM=AD=2,∴△AMD是等边三角形,∴AM=DM,
∴平行四边形AMDN是菱形,
26、如图,菱形的三个顶点、、分别在正方形的边、、上,连接.
求证:;
当时,求证:菱形为正方形.
【详解】(1)连接,∵,∴,
∵,∴,∴;
∵四边形是正方形,∴,
∵四边形是菱形,∴,
在和中,,∴,
∴, 又∵,
∴,∴,∴菱形为正方形;
27、(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF= .若AB=4,则△CEF的周长为 .
(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
【答案】解:(1)延长EB至H,使BH=DF,连接AH,如图1,
∵在正方形ABCD中,∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,,∴△ADF≌△ABH(SAS),∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,,∴△FAE≌△HAE(SAS),∴EF=HE=BE+HB,
∴EF=BE+DF,∴△CEF的周长=EF+CE+CF=BE+CE+DF+CF=BC+CD=2AB=8.
故答案为:EF;8.
(2)EF=BE+DF,理由如下:
延长CB至M,使BM=DF,连接AM,如图2,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,∴∠D=∠ABM,
在△ABM和△ADF中,,∴△ABM≌△ADF(SAS),∴AF=AM,∠DAF=∠BAM,
∵∠BAD=∠C=90°,∠EAF=45°,即∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,,∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,即EF=BE+DF.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
