周末阶段复习提升训练卷1(图形的旋转、中心对称、平行四边形)-2020-2021学年苏科版八年级数学下册含答案
文档属性
| 名称 | 周末阶段复习提升训练卷1(图形的旋转、中心对称、平行四边形)-2020-2021学年苏科版八年级数学下册含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 19:50:20 | ||
图片预览

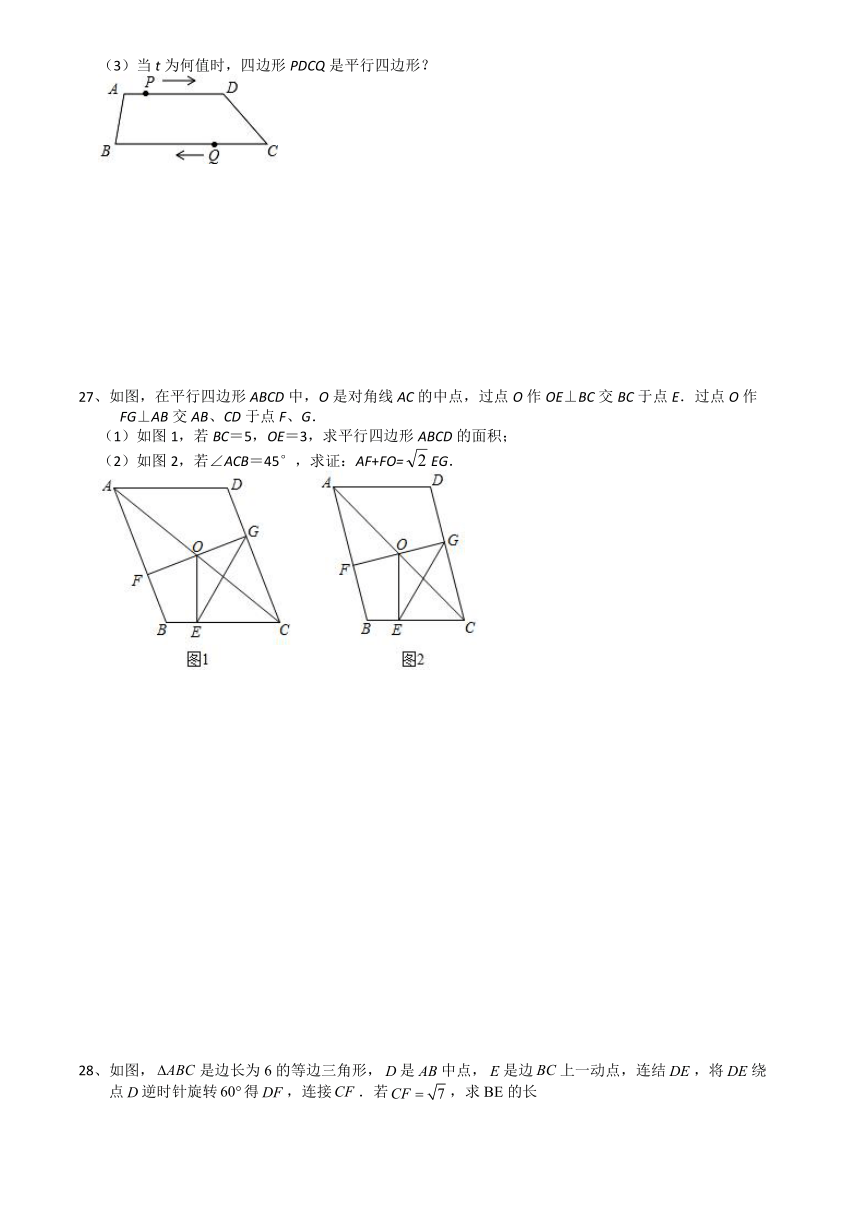
文档简介
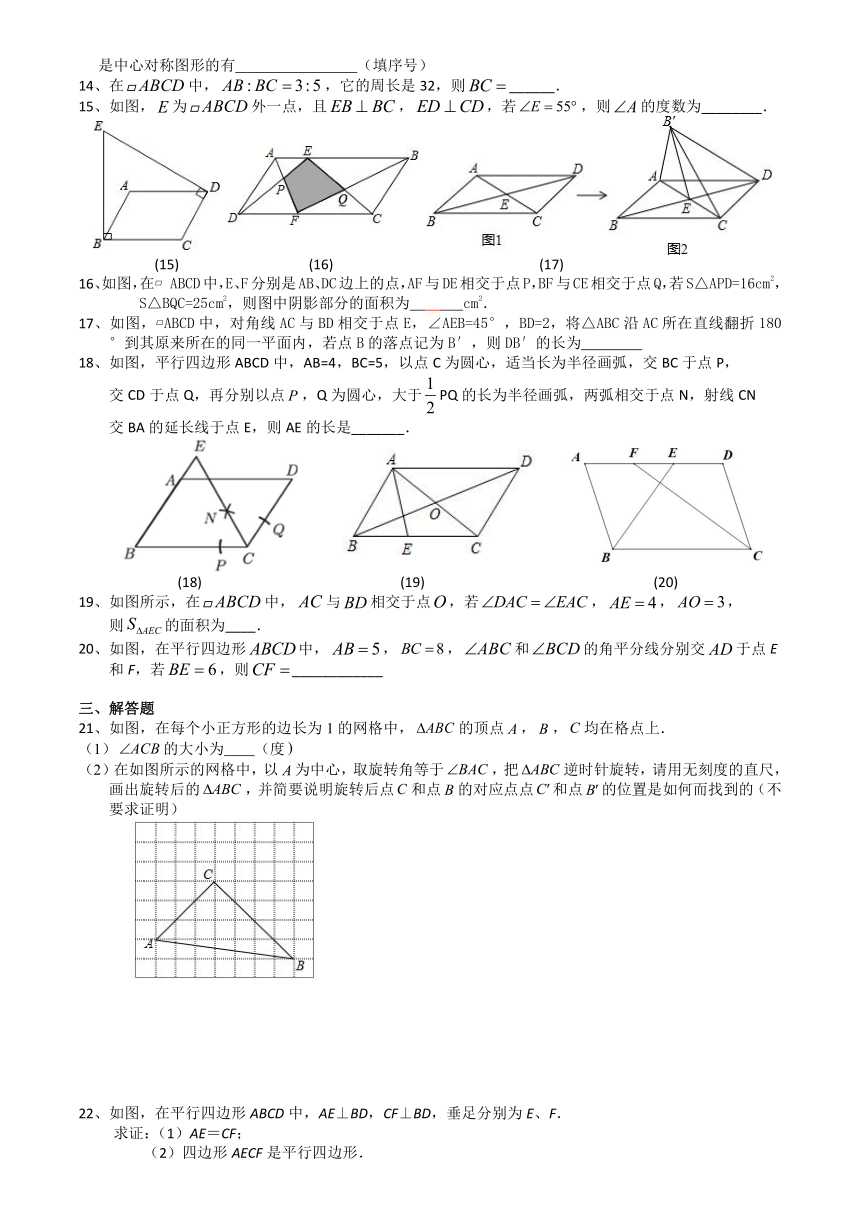
阶段复习提升训练卷(图形的旋转、中心对称、平行四边形)-20-21苏科版八年级数学下册
一、选择题
1、民族图案是数学文化中的一块瑰宝.下列图案中,是轴对称图形但不是中心对称图形的是
A. B. C. D.
2、等边三角形绕着它的中心旋转,若旋转后的三角形能与自身重合,则旋转角最小是
A. B. C. D.
3、如图,在中,,将绕点逆时针旋转角到的位置,这时点恰好落在边的中点,则旋转角的度数为
A. B. C. D.
(4) (7)
4、如图,将绕点顺时针旋转得到,若,,,
则的面积为 .
5、将绕点旋转得到,则下列作图正确的是
A. B. C. D.
6、一个图形旋转后得到的图形与原来的图形有如下的关系
对应角相等;对应线段相等;对应点到旋转中心的距离相等;连接对应点所成的线段相等;每对对应点与旋转中心连线所成的角都相等,它们都等于旋转角;其中正确的有
A. 5个 B. 4个 C. 3个 D. 2个
7、如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
8、如图在中,对角线相交于点O,与的周长相差3,,
那么为( )
A.5 B.8 C.11或5 D.11或14
(9) (11)
9、如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,BC=10,则EF长为( )
A.1 B.1.5 C.2 D.2.5
10、已知平行四边形,对角线、,
则该平行四边形四条边中最长边a的取值范围是( )
A. B. C. D.
二、填空题
11、把图中的风筝图案,绕着它的中心旋转,旋转角至少为 度时,旋转后的图形能与原来的图形重合.
12、在下列图形中:等腰三角形、等边三角形、正方形、正五边形、平行四边形、等腰梯形,其中有 个旋转对称图形.
13、下列图形中,①等腰三角形;②平行四边形;③等腰梯形;④圆;⑤正六边形;⑥菱形;⑦正五边形,是中心对称图形的有 (填序号)
14、在中,,它的周长是32,则______.
15、如图,为外一点,且,,若,则的度数为________.
(15) (16) (17)
16、如图,在?ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为 cm2.
17、如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为
18、如图,平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,
交CD于点Q,再分别以点,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN
交BA的延长线于点E,则AE的长是_______.
(19) (20)
19、如图所示,在中,与相交于点,若,,,
则的面积为____.
20、如图,在平行四边形中,,,和的角平分线分别交于点E和F,若,则____________
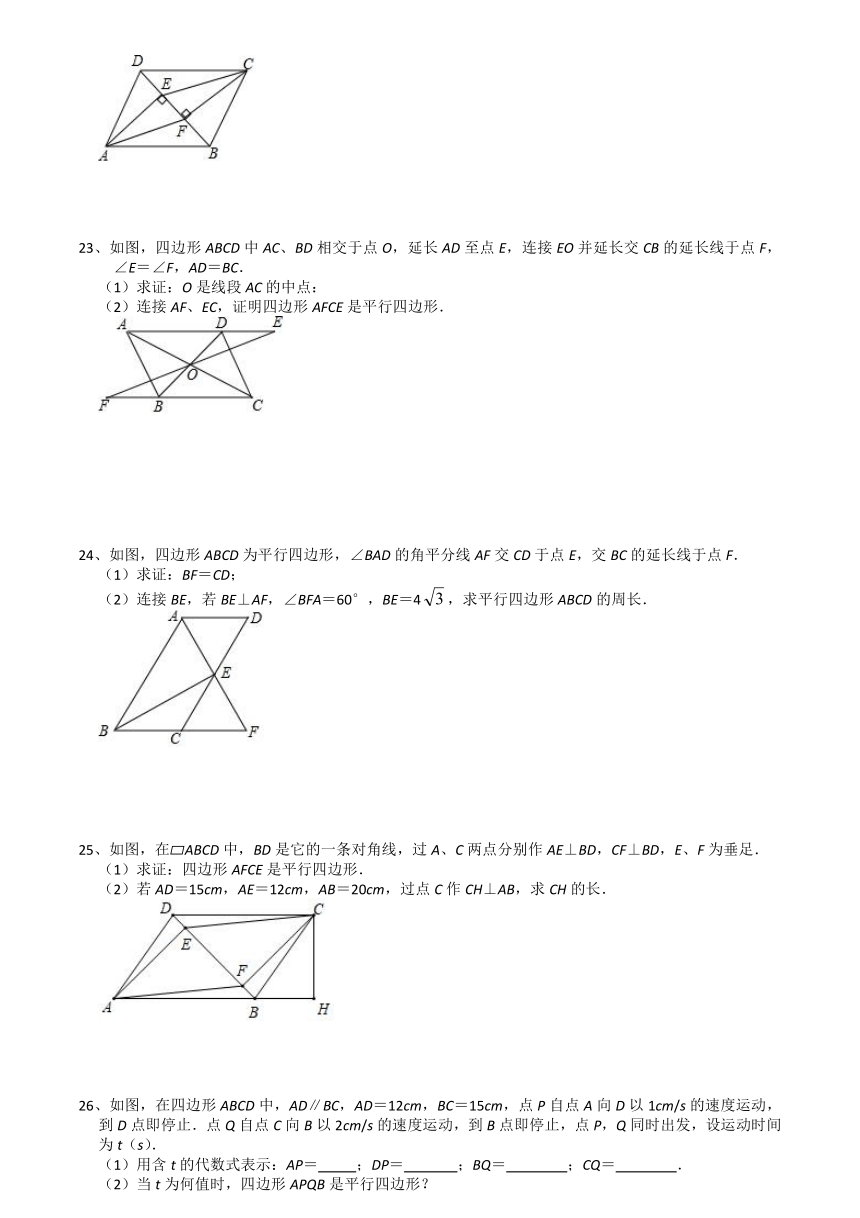
三、解答题
21、如图,在每个小正方形的边长为1的网格中,的顶点,,均在格点上.
(1)的大小为 (度
(2)在如图所示的网格中,以为中心,取旋转角等于,把逆时针旋转,请用无刻度的直尺,画出旋转后的,并简要说明旋转后点和点的对应点点和点的位置是如何而找到的(不要求证明)
22、如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
23、如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
24、如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=4,求平行四边形ABCD的周长.
25、如图,在?ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.
(1)求证:四边形AFCE是平行四边形.
(2)若AD=15cm,AE=12cm,AB=20cm,过点C作CH⊥AB,求CH的长.
26、如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
27、如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作OE⊥BC交BC于点E.过点O作
FG⊥AB交AB、CD于点F、G.
(1)如图1,若BC=5,OE=3,求平行四边形ABCD的面积;
(2)如图2,若∠ACB=45°,求证:AF+FO=EG.
28、如图,是边长为6的等边三角形,是中点,是边上一动点,连结,将绕
点逆时针旋转得,连接.若,求BE的长
29、如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.
(1)求证:AE=BC;
(2)如图(2),过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到
△AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
如图,P是正方形ABCD内一点,连接PA、PB、PC,将?ABP绕点B顺时针旋转到的位置.
(1)旋转中心是点______ ,点P旋转的度数是______ 度;
(2)连接,的形状是______ 三角形;
(3)若PA=2,PB=4,?APB=135.
求的周长;
求PC的长.
31、在? ABCD 中,BE 平分∠ABC 交 AD 于点 E.
(1)如图 1,若∠D=30°,AB=,求△ABE 的面积;
(2)如图 2,过点 A 作 AF⊥DC,交 DC 的延长线于点 F,分别交 BE,BC 于点 G,H, 且 AB=AF.
求证:ED﹣AG=FC.
阶段复习提升训练卷(图形的旋转、中心对称、平行四边形)-20-21苏科版八年级数学下册(答案)
一、选择题
1、民族图案是数学文化中的一块瑰宝.下列图案中,是轴对称图形但不是中心对称图形的是
A. B. C. D.
【解析】、不是轴对称图形,是中心对称图形,故本选项错误;
、是轴对称图形,不是中心对称图形,故本选项正确;
.既不是轴对称,也不是中心对称图形,故本选项错误;
、是轴对称图形,也是中心对称图形,故本选项错误.
故选:.
2、等边三角形绕着它的中心旋转,若旋转后的三角形能与自身重合,则旋转角最小是
A. B. C. D.
【解析】,该图形绕中心至少旋转120度后能和原来的图案互相重合.
故选:.
3、如图,在中,,将绕点逆时针旋转角到的位置,这时点恰好落在边的中点,则旋转角的度数为
A. B. C. D.
【解析】,为的中点,,
将绕点逆时针旋转角到的位置,,,
为等边三角形,,,故选:.
4、如图,将绕点顺时针旋转得到,若,,,
则的面积为 .
【解析】将绕点顺时针旋转得到,,,
是等边三角形,,的面积,
故答案为:.
5、将绕点旋转得到,则下列作图正确的是
A. B. C. D.
【解析】与关于点中心对称的只有选项.故选:.
6、一个图形旋转后得到的图形与原来的图形有如下的关系
对应角相等;对应线段相等;对应点到旋转中心的距离相等;连接对应点所成的线段相等;每对对应点与旋转中心连线所成的角都相等,它们都等于旋转角;其中正确的有
A. 5个 B. 4个 C. 3个 D. 2个
解答:B
7、如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
解:A、∵,∴AO=CO,
由于四边形ABCD是平行四边形,则BO=DO,∴四边形DEBF是平行四边形;
B、不能证明四边形DEBF是平行四边形;
C、∵四边形ABCD是平行四边形,∴AD=BC,∠DAE=∠BCF,又∠ADE=∠CBF,
∴△DAE≌△BCF(ASA), ∴AE=CF,同A可证四边形DEBF是平行四边形;
D、同C可证:△ABE≌△CDF(ASA),∴AE=CF,同A可证四边形DEBF是平行四边形;
故选:B.
8、如图在中,对角线相交于点O,与的周长相差3,,
那么为( )
A.5 B.8 C.11或5 D.11或14
解:∵四边形ABCD是平行四边形,∴BO=DO,AO=AO,
∵与的周长相差3,∴AB-AD=3,或AD-AB=3,
∵AB=8,∴AD的长为5或11, 故选C.
9、如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,BC=10,则EF长为( )
A.1 B.1.5 C.2 D.2.5
【详解】∵四边形是平行四边形,∴,,,
∴,∴平分,∴,∴,
∴, 同理可得,
∴.故选:.
10、已知平行四边形,对角线、,
则该平行四边形四条边中最长边a的取值范围是( )
A. B. C. D.
解:如图所示:四边形ABCD是平行四边形,AD>AB, ,,
在△AOD中,由三角形的三边关系得:4-3<AD<4+3,∴1<AD<7,
当四边相等时易得边长为5,∴5≤AD<7.故选:B.
二、填空题
11、把图中的风筝图案,绕着它的中心旋转,旋转角至少为 度时,旋转后的图形能与原来的图形重合.
【解析】该图形被平分成四部分,旋转90度的整数倍,就可以与自身重合,旋转角至少为.
故答案为:90
12、在下列图形中:等腰三角形、等边三角形、正方形、正五边形、平行四边形、等腰梯形,其中有 个旋转对称图形.
【解析】在等腰三角形、等边三角形、正方形、正五边形、平行四边形、等腰梯形中
只有等边三角形、正方形、正五边形、平行四边形是旋转对称图形.
故答案为4;
13、下列图形中,①等腰三角形;②平行四边形;③等腰梯形;④圆;⑤正六边形;⑥菱形;⑦正五边形,是中心对称图形的有 (填序号)
【解析】是中心对称图形的有:②平行四边形;④圆;⑤正六边形;⑥菱形.
故答案为:②④⑤⑥.
14、在中,,它的周长是32,则______.
解:设
由题意得, 解得
所以BC=10. 故答案为10.
15、如图,为外一点,且,,若,则的度数为________.
【详解】∵,,∴.
∵,∴,且,∴.
∵四边形是平行四边形,∴. 故答案为:.
16、如图,在?ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为 41 cm2.
17、如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为
解答:解:∵四边形ABCD是平行四边形,BD=2,∴BE=BD=1.
如图2,连接BB′.根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.
∴∠BEB′=90°,∴△BB′E是等腰直角三角形,则BB′=BE=.
又∵BE=DE,B′E⊥BD,∴DB′=BB′=. 故答案是:.
18、如图,平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,
交CD于点Q,再分别以点,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN
交BA的延长线于点E,则AE的长是_______.
【详解】由作图可知,平分,.
四边形是平行四边形,,,,
.
∵AB=4,,. 故答案为1.
19、如图所示,在中,与相交于点,若,,,
则的面积为____.
解:如图1,连接OE,∵四边形ABCD是平行四边形,∴OA=OC=3,AD∥BC,∴∠DAC=∠ACB,
又∵,∴∠ACB=∠EAC,∴AE=EC=4,
∴△AEC是等腰三角形,∴OE⊥AC,
在Rt△AOE中,由勾股定理得,AO2+OE2=AE2,∴32+OE2=42,∴OE=,
∴, 故答案是:.
20、如图,在平行四边形中,,,和的角平分线分别交于点E和F,若,则____________
【详解】平行四边形中,平分,平分,
∴,,
∵,∴,,,
∴,,,
∴AE=AB=5,DF=DC=5, ∵AD=BC=8,∴AF=AD-DF=3,∴EF=AE-AF=2,
延长使,∴为平行四边形,
∴,,, ∴,∴
∵,,
∴,∴.故答案为:8.
三、解答题
21、如图,在每个小正方形的边长为1的网格中,的顶点,,均在格点上.
(1)的大小为 (度
(2)在如图所示的网格中,以为中心,取旋转角等于,把逆时针旋转,请用无刻度的直尺,画出旋转后的,并简要说明旋转后点和点的对应点点和点的位置是如何而找到的(不要求证明)
【解析】(1),,,,
,故答案为90.
(2)如图,延长到格点,使得,取格点,,,,连接,交于点,取格点,.,,连接,交于点,作直线,直线交于点,△即为所求.
22、如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
【解析】证明:(1)∵四边形ABCD是平行四边形.∴AD∥BC,AD=BC.∴∠ADE=∠CBF.
∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB=90°.
∵在△ADE与△CBF中,∴△ADE≌△CBF(AAS),∴AE=CF.
(2)∵AE⊥BD,CF⊥BD,∴∠AEF=∠CFE=90°.∴AE∥CF.
又∵AE=CF,∴四边形AECF是平行四边形.
23、如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
【解析】证明:(1)∵∠E=∠F,∴AD∥BC,
∵AD=BC,∴四边形ABCD是平行四边形,∴AC,BD互相平分;即O是线段AC的中点.
(2)∵AD∥BC,∴∠EAC=∠FCA,
在△OAE和△OCF中,, ∴△OAE≌△OCF(ASA).
∴OE=OF,∴四边形AFCE是平行四边形.
24、如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=4,求平行四边形ABCD的周长.
【解析】(1)∵四边形ABCD为平行四边形,∴AB=CD,AD∥BC,∴∠FAD=∠AFB,
又∵AF平分∠BAD,∴∠FAD=∠FAB.∴∠AFB=∠FAB.∴AB=BF,∴BF=CD;
(2)解:由(1)知:AB=BF,
又∵∠BFA=60°,∴△ABF为等边三角形,∴AF=BF=AB,∠ABF=60°,
∵BE⊥AF,∴点E是AF的中点.
在Rt△BEF中,∠BFA=60°,BE=4,∴EF=4,BF=8,∴AB=BF=8,
∵四边形BACD是平行四边形,∴AB=CD,AD=BC,AB∥CD,
∴∠DCF=∠ABC=60°=∠F,∴CE=EF,∴△ECF是等边三角形,
∴CE=EF=CF=4,∴BC=8﹣4=4,
∴平行四边形ABCD的周长为8+8+4+4=24.
25、如图,在?ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.
(1)求证:四边形AFCE是平行四边形.
(2)若AD=15cm,AE=12cm,AB=20cm,过点C作CH⊥AB,求CH的长.
【解析】(1)证明:如图,连接AC交BD于点O
∵四边形ABCD是平行四边形,∴AD=BC,AO=CO,
∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°,
在△AOE和△COF中,,∴△AOE≌△COF(AAS),∴EO=FO,
∵AO=CO,∴四边形AECF是平行四边形;
(2)解:在Rt△ABE中,由勾股定理得:BE==16,
在Rt△AED中,由勾股定理得:DE=9, ∴BD=16+9=25,
∴S?ABCD=2S△ABD=2××25×12=AB×CH=20CH, ∴CH=15.
26、如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
【解析】(1)t,12﹣t,15﹣2t,2t
(2)根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴t=5s时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,∴PD=AD﹣AP=12﹣t,
如图1,∵AD∥BC,∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,解得t=4s, ∴当t=4s时,四边形PDCQ是平行四边形.
27、如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作OE⊥BC交BC于点E.过点O作
FG⊥AB交AB、CD于点F、G.
(1)如图1,若BC=5,OE=3,求平行四边形ABCD的面积;
(2)如图2,若∠ACB=45°,求证:AF+FO=EG.
【解析】(1)连接BD,∵平行四边形ABCD,∴BD过点O,
∴S△OBC=BC?OE=×5×3=, ∴平行四边形ABCD的面积=4S△OBC=30;
(2)过点E作EH⊥EG,与GC的延长线交于点H,如图2,
∵OE⊥BC,∴∠OEG+∠OEC=∠GEC+∠CEH=90°,∴∠OEG=∠CEH,
∵∠ACB=45°,∴∠COE=45°,∴OE=CE,
∵平行四边形ABCD中,AB∥CD, 又FG⊥AB,∴FG⊥CD,
∴∠EOG+∠ECG=360°﹣90°﹣90°=180°,
∵∠ECH+∠ECG=180°,∴∠EOG=∠ECH,∴△OEG≌△CEH(ASA),
∴OG=CH,EG=EH,
∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,∴∠OAF=∠OCG,
∵∠AOF=∠COG,∴△OAF≌△OCG(ASA),∴AF=CG,OF=OG,
∵CG+CH=GH,∴AF+OF=GH,
∵∠GEH=90°,EG=EH,∴GH=EG,∴AF+OF=EG.
28、如图,是边长为6的等边三角形,是中点,是边上一动点,连结,将绕
点逆时针旋转得,连接.若,求BE的长
【解析】连接,当点在直线的右侧时,如图1中,取的中点,连接,,延长 交于,
是等边三角形,,,
,,,是等边三角形,
,,,
,,,,
,,,,,
,,,,
,,,,,
,, .
当点在直线的左侧时,如图2中,同法可得,
综上所述,满足条件的的值为1或2.
29、如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.
(1)求证:AE=BC;
(2)如图(2),过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到
△AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
【解答】(1)证明:∵AB=BC,∠A=36°,∴∠ABC=∠C=72°,又∵BE平分∠ABC,∴∠ABE=∠CBE=36°,
∴∠BEC=180°﹣∠C﹣∠CBE=72°,∴∠ABE=∠A,∠BEC=∠C,
∴AE=BE,BE=BC,∴AE=BC.
(2)证明:∵AC=AB且EF∥BC,∴AE=AF;
由旋转的性质可知:∠E′AC=∠F′AB,AE′=AF′,∵在△CAE′和△BAF′中,
∴△CAE′≌△BAF′,∴CE′=BF′.
(3)存在CE′∥AB,
理由:由(1)可知AE=BC,所以,在△AEF绕点A逆时针旋转过程中,E点经过的路径(圆弧)与过点C且与AB平行的直线l交于M、N两点,
如图:①当点E的像E′与点M重合时,则四边形ABCM为等腰梯形,
∴∠BAM=∠ABC=72°,又∠BAC=36°,∴α=∠CAM=36°.
②当点E的像E′与点N重合时,由AB∥l得,∠AMN=∠BAM=72°,
∵AM=AN,∴∠ANM=∠AMN=72°,∴∠MAN=180°﹣2×72°=36°,
∴α=∠CAN=∠CAM+∠MAN=72°.
所以,当旋转角为36°或72°时,CE′∥AB.
30、如图,P是正方形ABCD内一点,连接PA、PB、PC,将?ABP绕点B顺时针旋转到的位置.
(1)旋转中心是点______ ,点P旋转的度数是______ 度;
(2)连接,的形状是______ 三角形;
(3)若PA=2,PB=4,?APB=135.
求的周长;
求PC的长.
解答:(1)∵P是正方形ABCD内一点,△ABP绕点B顺时针旋转到△CBP′的位置,
∴旋转中心是点B,点P旋转的度数是90度;
(2)根据旋转的性质BP=BP′,∵旋转角为90°,∴△BPP′是等腰直角三角形;
(3)①∵PB=4,∴PP′=,
∴△BPP′的周长=PB+P′B+PP′=;
②∵∠BP′C=∠BPA=135°,∴∠PP′C=∠BP′C﹣∠BP′P=135°﹣45°=90°,
在Rt△PP′C中,PC=.
31、在? ABCD 中,BE 平分∠ABC 交 AD 于点 E.
(1)如图 1,若∠D=30°,AB=,求△ABE 的面积;
(2)如图 2,过点 A 作 AF⊥DC,交 DC 的延长线于点 F,分别交 BE,BC 于点 G,H, 且 AB=AF.
求证:ED﹣AG=FC.
【解答】(1)解:作BO⊥AD于O,如图1所示:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,∠ABC=∠D=30°,∴∠AEB=∠CBE,∠BAO=∠D=30°,
∴BQ=AB=,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABE=∠AEB,
∴AE=AB=,∴△ABE的面积=AE×BO=××=;
(2)证明:作AQ⊥BE交DF的延长线于P,垂足为Q,连接PB、PE,如图2所示:
∵AB=AE,AQ⊥BE,∴∠ABE=∠AEB,BQ=EQ,∴PB=PE,∴∠PBE=∠PEB,
∴∠ABP=∠AEP,∵AB∥CD,AF⊥CD,∴AF⊥AB,∴∠BAF=90°,∵AQ⊥BE,
∴∠ABG=∠FAP,在△ABG和△FAP中,,∴△ABG≌△AFP(ASA),
∴AG=FP,∵AB∥CD,AD∥BC,∴∠ABP+∠BPC=180°,∠BCP=∠D,
∵∠AEP+∠PED=180°,∴∠BPC=∠PED, 在△BPC和△PED中,,
∴△BPC≌△PED(AAS),∴PC=ED,∴ED﹣AG=PC﹣AG=PC﹣FP=FC.
一、选择题
1、民族图案是数学文化中的一块瑰宝.下列图案中,是轴对称图形但不是中心对称图形的是
A. B. C. D.
2、等边三角形绕着它的中心旋转,若旋转后的三角形能与自身重合,则旋转角最小是
A. B. C. D.
3、如图,在中,,将绕点逆时针旋转角到的位置,这时点恰好落在边的中点,则旋转角的度数为
A. B. C. D.
(4) (7)
4、如图,将绕点顺时针旋转得到,若,,,
则的面积为 .
5、将绕点旋转得到,则下列作图正确的是
A. B. C. D.
6、一个图形旋转后得到的图形与原来的图形有如下的关系
对应角相等;对应线段相等;对应点到旋转中心的距离相等;连接对应点所成的线段相等;每对对应点与旋转中心连线所成的角都相等,它们都等于旋转角;其中正确的有
A. 5个 B. 4个 C. 3个 D. 2个
7、如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
8、如图在中,对角线相交于点O,与的周长相差3,,
那么为( )
A.5 B.8 C.11或5 D.11或14
(9) (11)
9、如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,BC=10,则EF长为( )
A.1 B.1.5 C.2 D.2.5
10、已知平行四边形,对角线、,
则该平行四边形四条边中最长边a的取值范围是( )
A. B. C. D.
二、填空题
11、把图中的风筝图案,绕着它的中心旋转,旋转角至少为 度时,旋转后的图形能与原来的图形重合.
12、在下列图形中:等腰三角形、等边三角形、正方形、正五边形、平行四边形、等腰梯形,其中有 个旋转对称图形.
13、下列图形中,①等腰三角形;②平行四边形;③等腰梯形;④圆;⑤正六边形;⑥菱形;⑦正五边形,是中心对称图形的有 (填序号)
14、在中,,它的周长是32,则______.
15、如图,为外一点,且,,若,则的度数为________.
(15) (16) (17)
16、如图,在?ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为 cm2.
17、如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为
18、如图,平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,
交CD于点Q,再分别以点,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN
交BA的延长线于点E,则AE的长是_______.
(19) (20)
19、如图所示,在中,与相交于点,若,,,
则的面积为____.
20、如图,在平行四边形中,,,和的角平分线分别交于点E和F,若,则____________
三、解答题
21、如图,在每个小正方形的边长为1的网格中,的顶点,,均在格点上.
(1)的大小为 (度
(2)在如图所示的网格中,以为中心,取旋转角等于,把逆时针旋转,请用无刻度的直尺,画出旋转后的,并简要说明旋转后点和点的对应点点和点的位置是如何而找到的(不要求证明)
22、如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
23、如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
24、如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=4,求平行四边形ABCD的周长.
25、如图,在?ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.
(1)求证:四边形AFCE是平行四边形.
(2)若AD=15cm,AE=12cm,AB=20cm,过点C作CH⊥AB,求CH的长.
26、如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
27、如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作OE⊥BC交BC于点E.过点O作
FG⊥AB交AB、CD于点F、G.
(1)如图1,若BC=5,OE=3,求平行四边形ABCD的面积;
(2)如图2,若∠ACB=45°,求证:AF+FO=EG.
28、如图,是边长为6的等边三角形,是中点,是边上一动点,连结,将绕
点逆时针旋转得,连接.若,求BE的长
29、如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.
(1)求证:AE=BC;
(2)如图(2),过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到
△AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
如图,P是正方形ABCD内一点,连接PA、PB、PC,将?ABP绕点B顺时针旋转到的位置.
(1)旋转中心是点______ ,点P旋转的度数是______ 度;
(2)连接,的形状是______ 三角形;
(3)若PA=2,PB=4,?APB=135.
求的周长;
求PC的长.
31、在? ABCD 中,BE 平分∠ABC 交 AD 于点 E.
(1)如图 1,若∠D=30°,AB=,求△ABE 的面积;
(2)如图 2,过点 A 作 AF⊥DC,交 DC 的延长线于点 F,分别交 BE,BC 于点 G,H, 且 AB=AF.
求证:ED﹣AG=FC.
阶段复习提升训练卷(图形的旋转、中心对称、平行四边形)-20-21苏科版八年级数学下册(答案)
一、选择题
1、民族图案是数学文化中的一块瑰宝.下列图案中,是轴对称图形但不是中心对称图形的是
A. B. C. D.
【解析】、不是轴对称图形,是中心对称图形,故本选项错误;
、是轴对称图形,不是中心对称图形,故本选项正确;
.既不是轴对称,也不是中心对称图形,故本选项错误;
、是轴对称图形,也是中心对称图形,故本选项错误.
故选:.
2、等边三角形绕着它的中心旋转,若旋转后的三角形能与自身重合,则旋转角最小是
A. B. C. D.
【解析】,该图形绕中心至少旋转120度后能和原来的图案互相重合.
故选:.
3、如图,在中,,将绕点逆时针旋转角到的位置,这时点恰好落在边的中点,则旋转角的度数为
A. B. C. D.
【解析】,为的中点,,
将绕点逆时针旋转角到的位置,,,
为等边三角形,,,故选:.
4、如图,将绕点顺时针旋转得到,若,,,
则的面积为 .
【解析】将绕点顺时针旋转得到,,,
是等边三角形,,的面积,
故答案为:.
5、将绕点旋转得到,则下列作图正确的是
A. B. C. D.
【解析】与关于点中心对称的只有选项.故选:.
6、一个图形旋转后得到的图形与原来的图形有如下的关系
对应角相等;对应线段相等;对应点到旋转中心的距离相等;连接对应点所成的线段相等;每对对应点与旋转中心连线所成的角都相等,它们都等于旋转角;其中正确的有
A. 5个 B. 4个 C. 3个 D. 2个
解答:B
7、如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
解:A、∵,∴AO=CO,
由于四边形ABCD是平行四边形,则BO=DO,∴四边形DEBF是平行四边形;
B、不能证明四边形DEBF是平行四边形;
C、∵四边形ABCD是平行四边形,∴AD=BC,∠DAE=∠BCF,又∠ADE=∠CBF,
∴△DAE≌△BCF(ASA), ∴AE=CF,同A可证四边形DEBF是平行四边形;
D、同C可证:△ABE≌△CDF(ASA),∴AE=CF,同A可证四边形DEBF是平行四边形;
故选:B.
8、如图在中,对角线相交于点O,与的周长相差3,,
那么为( )
A.5 B.8 C.11或5 D.11或14
解:∵四边形ABCD是平行四边形,∴BO=DO,AO=AO,
∵与的周长相差3,∴AB-AD=3,或AD-AB=3,
∵AB=8,∴AD的长为5或11, 故选C.
9、如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,BC=10,则EF长为( )
A.1 B.1.5 C.2 D.2.5
【详解】∵四边形是平行四边形,∴,,,
∴,∴平分,∴,∴,
∴, 同理可得,
∴.故选:.
10、已知平行四边形,对角线、,
则该平行四边形四条边中最长边a的取值范围是( )
A. B. C. D.
解:如图所示:四边形ABCD是平行四边形,AD>AB, ,,
在△AOD中,由三角形的三边关系得:4-3<AD<4+3,∴1<AD<7,
当四边相等时易得边长为5,∴5≤AD<7.故选:B.
二、填空题
11、把图中的风筝图案,绕着它的中心旋转,旋转角至少为 度时,旋转后的图形能与原来的图形重合.
【解析】该图形被平分成四部分,旋转90度的整数倍,就可以与自身重合,旋转角至少为.
故答案为:90
12、在下列图形中:等腰三角形、等边三角形、正方形、正五边形、平行四边形、等腰梯形,其中有 个旋转对称图形.
【解析】在等腰三角形、等边三角形、正方形、正五边形、平行四边形、等腰梯形中
只有等边三角形、正方形、正五边形、平行四边形是旋转对称图形.
故答案为4;
13、下列图形中,①等腰三角形;②平行四边形;③等腰梯形;④圆;⑤正六边形;⑥菱形;⑦正五边形,是中心对称图形的有 (填序号)
【解析】是中心对称图形的有:②平行四边形;④圆;⑤正六边形;⑥菱形.
故答案为:②④⑤⑥.
14、在中,,它的周长是32,则______.
解:设
由题意得, 解得
所以BC=10. 故答案为10.
15、如图,为外一点,且,,若,则的度数为________.
【详解】∵,,∴.
∵,∴,且,∴.
∵四边形是平行四边形,∴. 故答案为:.
16、如图,在?ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为 41 cm2.
17、如图,?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为
解答:解:∵四边形ABCD是平行四边形,BD=2,∴BE=BD=1.
如图2,连接BB′.根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.
∴∠BEB′=90°,∴△BB′E是等腰直角三角形,则BB′=BE=.
又∵BE=DE,B′E⊥BD,∴DB′=BB′=. 故答案是:.
18、如图,平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,
交CD于点Q,再分别以点,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN
交BA的延长线于点E,则AE的长是_______.
【详解】由作图可知,平分,.
四边形是平行四边形,,,,
.
∵AB=4,,. 故答案为1.
19、如图所示,在中,与相交于点,若,,,
则的面积为____.
解:如图1,连接OE,∵四边形ABCD是平行四边形,∴OA=OC=3,AD∥BC,∴∠DAC=∠ACB,
又∵,∴∠ACB=∠EAC,∴AE=EC=4,
∴△AEC是等腰三角形,∴OE⊥AC,
在Rt△AOE中,由勾股定理得,AO2+OE2=AE2,∴32+OE2=42,∴OE=,
∴, 故答案是:.
20、如图,在平行四边形中,,,和的角平分线分别交于点E和F,若,则____________
【详解】平行四边形中,平分,平分,
∴,,
∵,∴,,,
∴,,,
∴AE=AB=5,DF=DC=5, ∵AD=BC=8,∴AF=AD-DF=3,∴EF=AE-AF=2,
延长使,∴为平行四边形,
∴,,, ∴,∴
∵,,
∴,∴.故答案为:8.
三、解答题
21、如图,在每个小正方形的边长为1的网格中,的顶点,,均在格点上.
(1)的大小为 (度
(2)在如图所示的网格中,以为中心,取旋转角等于,把逆时针旋转,请用无刻度的直尺,画出旋转后的,并简要说明旋转后点和点的对应点点和点的位置是如何而找到的(不要求证明)
【解析】(1),,,,
,故答案为90.
(2)如图,延长到格点,使得,取格点,,,,连接,交于点,取格点,.,,连接,交于点,作直线,直线交于点,△即为所求.
22、如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
【解析】证明:(1)∵四边形ABCD是平行四边形.∴AD∥BC,AD=BC.∴∠ADE=∠CBF.
∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB=90°.
∵在△ADE与△CBF中,∴△ADE≌△CBF(AAS),∴AE=CF.
(2)∵AE⊥BD,CF⊥BD,∴∠AEF=∠CFE=90°.∴AE∥CF.
又∵AE=CF,∴四边形AECF是平行四边形.
23、如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
【解析】证明:(1)∵∠E=∠F,∴AD∥BC,
∵AD=BC,∴四边形ABCD是平行四边形,∴AC,BD互相平分;即O是线段AC的中点.
(2)∵AD∥BC,∴∠EAC=∠FCA,
在△OAE和△OCF中,, ∴△OAE≌△OCF(ASA).
∴OE=OF,∴四边形AFCE是平行四边形.
24、如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=4,求平行四边形ABCD的周长.
【解析】(1)∵四边形ABCD为平行四边形,∴AB=CD,AD∥BC,∴∠FAD=∠AFB,
又∵AF平分∠BAD,∴∠FAD=∠FAB.∴∠AFB=∠FAB.∴AB=BF,∴BF=CD;
(2)解:由(1)知:AB=BF,
又∵∠BFA=60°,∴△ABF为等边三角形,∴AF=BF=AB,∠ABF=60°,
∵BE⊥AF,∴点E是AF的中点.
在Rt△BEF中,∠BFA=60°,BE=4,∴EF=4,BF=8,∴AB=BF=8,
∵四边形BACD是平行四边形,∴AB=CD,AD=BC,AB∥CD,
∴∠DCF=∠ABC=60°=∠F,∴CE=EF,∴△ECF是等边三角形,
∴CE=EF=CF=4,∴BC=8﹣4=4,
∴平行四边形ABCD的周长为8+8+4+4=24.
25、如图,在?ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.
(1)求证:四边形AFCE是平行四边形.
(2)若AD=15cm,AE=12cm,AB=20cm,过点C作CH⊥AB,求CH的长.
【解析】(1)证明:如图,连接AC交BD于点O
∵四边形ABCD是平行四边形,∴AD=BC,AO=CO,
∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°,
在△AOE和△COF中,,∴△AOE≌△COF(AAS),∴EO=FO,
∵AO=CO,∴四边形AECF是平行四边形;
(2)解:在Rt△ABE中,由勾股定理得:BE==16,
在Rt△AED中,由勾股定理得:DE=9, ∴BD=16+9=25,
∴S?ABCD=2S△ABD=2××25×12=AB×CH=20CH, ∴CH=15.
26、如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP= ;DP= ;BQ= ;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
【解析】(1)t,12﹣t,15﹣2t,2t
(2)根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴t=5s时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,∴PD=AD﹣AP=12﹣t,
如图1,∵AD∥BC,∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,解得t=4s, ∴当t=4s时,四边形PDCQ是平行四边形.
27、如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作OE⊥BC交BC于点E.过点O作
FG⊥AB交AB、CD于点F、G.
(1)如图1,若BC=5,OE=3,求平行四边形ABCD的面积;
(2)如图2,若∠ACB=45°,求证:AF+FO=EG.
【解析】(1)连接BD,∵平行四边形ABCD,∴BD过点O,
∴S△OBC=BC?OE=×5×3=, ∴平行四边形ABCD的面积=4S△OBC=30;
(2)过点E作EH⊥EG,与GC的延长线交于点H,如图2,
∵OE⊥BC,∴∠OEG+∠OEC=∠GEC+∠CEH=90°,∴∠OEG=∠CEH,
∵∠ACB=45°,∴∠COE=45°,∴OE=CE,
∵平行四边形ABCD中,AB∥CD, 又FG⊥AB,∴FG⊥CD,
∴∠EOG+∠ECG=360°﹣90°﹣90°=180°,
∵∠ECH+∠ECG=180°,∴∠EOG=∠ECH,∴△OEG≌△CEH(ASA),
∴OG=CH,EG=EH,
∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,∴∠OAF=∠OCG,
∵∠AOF=∠COG,∴△OAF≌△OCG(ASA),∴AF=CG,OF=OG,
∵CG+CH=GH,∴AF+OF=GH,
∵∠GEH=90°,EG=EH,∴GH=EG,∴AF+OF=EG.
28、如图,是边长为6的等边三角形,是中点,是边上一动点,连结,将绕
点逆时针旋转得,连接.若,求BE的长
【解析】连接,当点在直线的右侧时,如图1中,取的中点,连接,,延长 交于,
是等边三角形,,,
,,,是等边三角形,
,,,
,,,,
,,,,,
,,,,
,,,,,
,, .
当点在直线的左侧时,如图2中,同法可得,
综上所述,满足条件的的值为1或2.
29、如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.
(1)求证:AE=BC;
(2)如图(2),过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到
△AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
【解答】(1)证明:∵AB=BC,∠A=36°,∴∠ABC=∠C=72°,又∵BE平分∠ABC,∴∠ABE=∠CBE=36°,
∴∠BEC=180°﹣∠C﹣∠CBE=72°,∴∠ABE=∠A,∠BEC=∠C,
∴AE=BE,BE=BC,∴AE=BC.
(2)证明:∵AC=AB且EF∥BC,∴AE=AF;
由旋转的性质可知:∠E′AC=∠F′AB,AE′=AF′,∵在△CAE′和△BAF′中,
∴△CAE′≌△BAF′,∴CE′=BF′.
(3)存在CE′∥AB,
理由:由(1)可知AE=BC,所以,在△AEF绕点A逆时针旋转过程中,E点经过的路径(圆弧)与过点C且与AB平行的直线l交于M、N两点,
如图:①当点E的像E′与点M重合时,则四边形ABCM为等腰梯形,
∴∠BAM=∠ABC=72°,又∠BAC=36°,∴α=∠CAM=36°.
②当点E的像E′与点N重合时,由AB∥l得,∠AMN=∠BAM=72°,
∵AM=AN,∴∠ANM=∠AMN=72°,∴∠MAN=180°﹣2×72°=36°,
∴α=∠CAN=∠CAM+∠MAN=72°.
所以,当旋转角为36°或72°时,CE′∥AB.
30、如图,P是正方形ABCD内一点,连接PA、PB、PC,将?ABP绕点B顺时针旋转到的位置.
(1)旋转中心是点______ ,点P旋转的度数是______ 度;
(2)连接,的形状是______ 三角形;
(3)若PA=2,PB=4,?APB=135.
求的周长;
求PC的长.
解答:(1)∵P是正方形ABCD内一点,△ABP绕点B顺时针旋转到△CBP′的位置,
∴旋转中心是点B,点P旋转的度数是90度;
(2)根据旋转的性质BP=BP′,∵旋转角为90°,∴△BPP′是等腰直角三角形;
(3)①∵PB=4,∴PP′=,
∴△BPP′的周长=PB+P′B+PP′=;
②∵∠BP′C=∠BPA=135°,∴∠PP′C=∠BP′C﹣∠BP′P=135°﹣45°=90°,
在Rt△PP′C中,PC=.
31、在? ABCD 中,BE 平分∠ABC 交 AD 于点 E.
(1)如图 1,若∠D=30°,AB=,求△ABE 的面积;
(2)如图 2,过点 A 作 AF⊥DC,交 DC 的延长线于点 F,分别交 BE,BC 于点 G,H, 且 AB=AF.
求证:ED﹣AG=FC.
【解答】(1)解:作BO⊥AD于O,如图1所示:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,∠ABC=∠D=30°,∴∠AEB=∠CBE,∠BAO=∠D=30°,
∴BQ=AB=,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABE=∠AEB,
∴AE=AB=,∴△ABE的面积=AE×BO=××=;
(2)证明:作AQ⊥BE交DF的延长线于P,垂足为Q,连接PB、PE,如图2所示:
∵AB=AE,AQ⊥BE,∴∠ABE=∠AEB,BQ=EQ,∴PB=PE,∴∠PBE=∠PEB,
∴∠ABP=∠AEP,∵AB∥CD,AF⊥CD,∴AF⊥AB,∴∠BAF=90°,∵AQ⊥BE,
∴∠ABG=∠FAP,在△ABG和△FAP中,,∴△ABG≌△AFP(ASA),
∴AG=FP,∵AB∥CD,AD∥BC,∴∠ABP+∠BPC=180°,∠BCP=∠D,
∵∠AEP+∠PED=180°,∴∠BPC=∠PED, 在△BPC和△PED中,,
∴△BPC≌△PED(AAS),∴PC=ED,∴ED﹣AG=PC﹣AG=PC﹣FP=FC.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
