周末阶段复习提升训练卷5(分式的混合运算))-2020-2021学年苏科版八年级数学下册含答案
文档属性
| 名称 | 周末阶段复习提升训练卷5(分式的混合运算))-2020-2021学年苏科版八年级数学下册含答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 992.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览
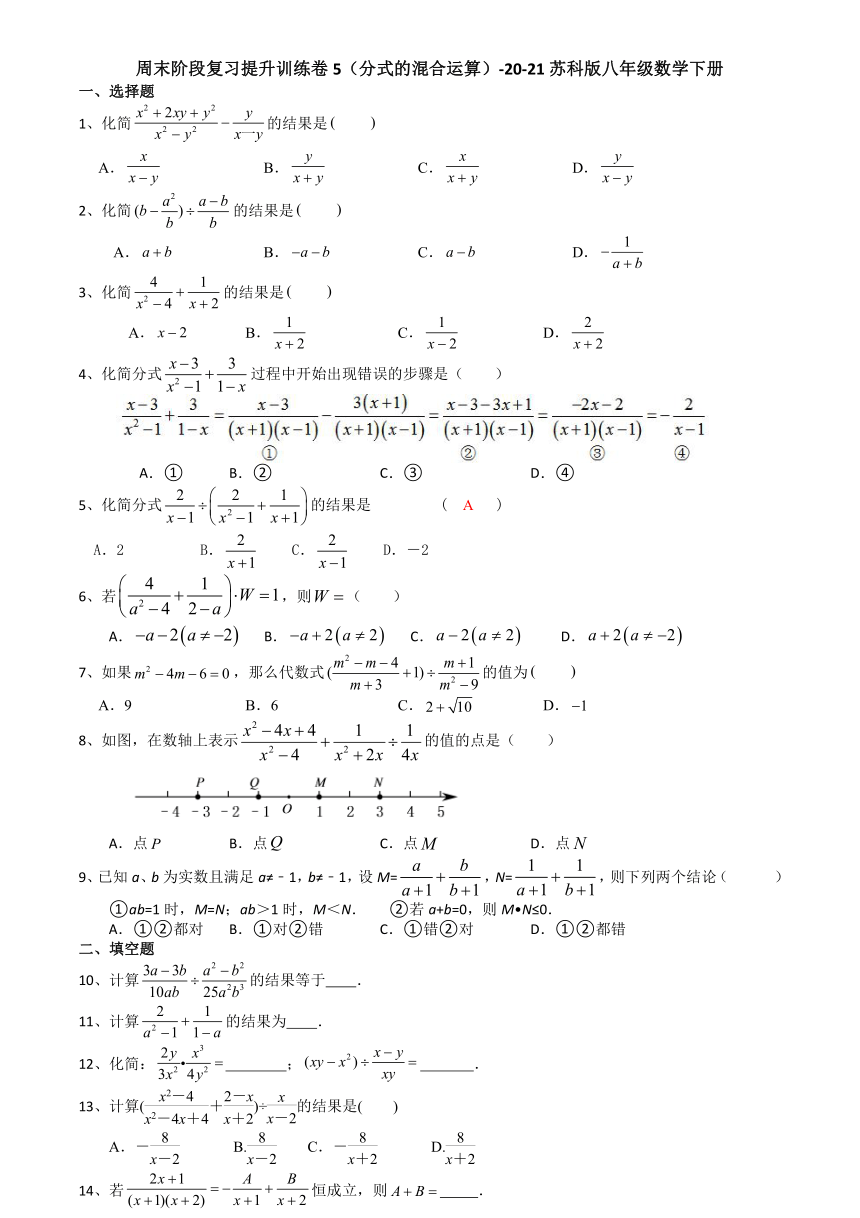




文档简介
周末阶段复习提升训练卷5(分式的混合运算)-20-21苏科版八年级数学下册
一、选择题
1、化简的结果是
A. B. C. D.
2、化简的结果是
A. B. C. D.
3、化简的结果是
A. B. C. D.
4、化简分式过程中开始出现错误的步骤是( )
A.① B.② C.③ D.④
5、化简分式的结果是 ( A )
A.2 B. C. D.-2
6、若,则( )
A. B. C. D.
7、如果,那么代数式的值为
A.9 B.6 C. D.
8、如图,在数轴上表示的值的点是( )
A.点 B.点 C.点 D.点
9、已知a、b为实数且满足a≠﹣1,b≠﹣1,设M=,N=,则下列两个结论( )
①ab=1时,M=N;ab>1时,M<N. ②若a+b=0,则M?N≤0.
A.①②都对 B.①对②错 C.①错②对 D.①②都错
二、填空题
10、计算的结果等于 .
11、计算的结果为 .
12、化简: ; .
13、计算(+)÷的结果是( )
A.- B. C.- D.
14、若恒成立,则 .
15、已知=5,则代数式的值为 .
16、如果a+b=2,那么的值是 .
17、如果,那么代数式的值是__________.
18、一种运算:规则是x※y=,根据此规则化简(m+1)※(m﹣1)的结果为 .
三、解答题
19、计算:
(1); (2).
20、(1)(1+)÷; (2)2+÷; (3)(a+)÷(1+).
21、先化简,再求值:
(1)(-)÷,其中a=+1.
(2)(1-)÷,其中a=-1.
(3)()· ,其中a=-.
22、先化简:÷(),再从-2<x<3的范围内选取一个你喜欢的x值代入求值.
23、已知a满足a2+2a-15=0,求-÷的值.
24、已知y=÷-x+3,试说明不论x为任何使原式有意义的值,y的值均不变.
25、分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式,例如:分式,是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.
例如,分式,是假分式,一个假分式可以化为一个整式与一个真分式的和.
例如:
(1)将假分式化为一个整数与一个真分式的和;
(2)利用上述方法解决问题:若是整数,且分式的值为正整数,求的值.
26、上课时老师在黑板上书写了一个分式的正确化简结果,随后用手掌盖住了一部分,形式如下:
(1)聪明的你请求出盖住部分化简后的结果
(2)当时,等于何值时,原分式的值为5
周末阶段复习提升训练卷5(分式的混合运算)-20-21苏科版八年级数学下册(答案)
一、选择题
1、化简的结果是
A. B. C. D.
【解析】原式,故选:.
2、化简的结果是
A. B. C. D.
【解析】原式.故选:.
3、化简的结果是
A. B. C. D.
【解析】;
故选:.
4、化简分式过程中开始出现错误的步骤是( )
A.① B.② C.③ D.④
解:∵
经过仔细比对,发现出错的步骤是题中所示②,分子相减时没有把第二个分子当作整体用括号括起来,
故选:B.
5、化简分式的结果是 ( A )
A.2 B. C. D.-2
6、若,则( )
A. B. C. D.
解:,
,
.
故选:.
7、如果,那么代数式的值为
A.9 B.6 C. D.
【解析】
,
,,原式, 故选:.
8、如图,在数轴上表示的值的点是( )
A.点 B.点 C.点 D.点
解:,
,
,
,
=1,
在数轴是对应的点是M,故选:C.
9、已知a、b为实数且满足a≠﹣1,b≠﹣1,设M=,N=,则下列两个结论( )
①ab=1时,M=N;ab>1时,M<N. ②若a+b=0,则M?N≤0.
A.①②都对 B.①对②错 C.①错②对 D.①②都错
【详解】∵M=,N= ,
∴①M﹣ N=﹣( ) =,
当ab=1时,M﹣N=0,∴M=N,
当ab>1时,2ab>2,∴2ab﹣2>0,
当a<0时,b<0,(a+1)(b+1)>0或(a+1)(b+1)<0,
∴M﹣N>0或M﹣N<0,
∴M>N或M<N; 故①错误;
②M?N=()?( )=.
∵a+b=0,∴原式==.
∵a≠﹣1,b≠﹣1,∴(a+1)2(b+1)2>0.
∵a+b=0,∴ab≤0,M?N≤0, 故②对.
故选:C.
二、填空题
10、计算的结果等于 .
【解析】.
故答案为:.
11、计算的结果为 .
【解析】原式
. 故答案为:.
12、化简: ; .
【解析】,
,
故答案为:、.
13、计算(+)÷的结果是( )
A.- B. C.- D.
[解析] 原式=·
=· =. 故选D
14、若恒成立,则 .
【解析】右边
,解,,,
故答案为4.
15、已知=5,则代数式的值为 .
【解析】∵=5,∴y﹣x=5xy,即x﹣y=﹣5xy.
∴ .
故答案为:.
16、如果a+b=2,那么的值是 .
【解析】原式
=a+b,
当a+b=2时,原式=2,故答案为:2.
17、如果,那么代数式的值是__________.
解:.
,,
.故答案为:.
18、一种运算:规则是x※y=,根据此规则化简(m+1)※(m﹣1)的结果为 .
【分析】根据所给规则列出算式,再通分,然后计算同分母的分式减法即可.
【解析】由题意得:(m+1)※(m﹣1),
,
,
,
=
故答案为:.
三、解答题
19、计算:
(1); (2).
【详解】(1)原式.
(2)原式
.
20、(1)(1+)÷; (2)2+÷; (3)(a+)÷(1+).
解:(1)(1+)÷=.
(2)2+÷=2-·=2-·
=2-=-==.
(3)原式=÷(+)=÷=·=a-1.
21、先化简,再求值:
(1)(-)÷,其中a=+1.
(2)(1-)÷,其中a=-1.
(3)()· ,其中a=-.
解:(1)原式=[-]·
=[-]·
=·
=.
将a=+1代入可得,原式==.
(2)(1-)÷=·=.
当a=-1时,原式===.
(3)原式=·=·=·=.
当a=-时,==-1.
22、先化简:÷(),再从-2<x<3的范围内选取一个你喜欢的x值代入求值.
解:原式=÷=·=.
由题意,可取x=2代入上式,得==4.(注意:x不能为0和±1)
23、已知a满足a2+2a-15=0,求-÷的值.
[解析] 对要求的式子进行计算,先进行因式分解,再把除法转化成乘法,然后进行约分,得到一个最简分式,最后把a2+2a-15=0进行配方,得到a+1的值,再把它整体代入即可求出答案.
解:-÷
=-·
=-=.
∵a2+2a-15=0,∴(a+1)2=16,
∴原式==.
24、已知y=÷-x+3,试说明不论x为任何使原式有意义的值,y的值均不变.
[解析] 先化简分式,再通过分析化简结果得出结论.
解:y=÷-x+3
=·-x+3
=x-x+3
=3.
由化简结果,可知y的值为常数3,与x的取值无关,
故不论x为任何使原式有意义的值,y的值均不变.
25、分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式,例如:分式,是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.
例如,分式,是假分式,一个假分式可以化为一个整式与一个真分式的和.
例如:
(1)将假分式化为一个整数与一个真分式的和;
(2)利用上述方法解决问题:若是整数,且分式的值为正整数,求的值.
【解析】(1)
(2)
分式的值为正整数
,
或或
或或
26、上课时老师在黑板上书写了一个分式的正确化简结果,随后用手掌盖住了一部分,形式如下:
(1)聪明的你请求出盖住部分化简后的结果
(2)当时,等于何值时,原分式的值为5
【解析】(1)
盖住部分化简后的结果为;
(2)时,原分式的值为5,即,
解得
经检验,是原方程的解.
所以当,时,原分式的值为5.
一、选择题
1、化简的结果是
A. B. C. D.
2、化简的结果是
A. B. C. D.
3、化简的结果是
A. B. C. D.
4、化简分式过程中开始出现错误的步骤是( )
A.① B.② C.③ D.④
5、化简分式的结果是 ( A )
A.2 B. C. D.-2
6、若,则( )
A. B. C. D.
7、如果,那么代数式的值为
A.9 B.6 C. D.
8、如图,在数轴上表示的值的点是( )
A.点 B.点 C.点 D.点
9、已知a、b为实数且满足a≠﹣1,b≠﹣1,设M=,N=,则下列两个结论( )
①ab=1时,M=N;ab>1时,M<N. ②若a+b=0,则M?N≤0.
A.①②都对 B.①对②错 C.①错②对 D.①②都错
二、填空题
10、计算的结果等于 .
11、计算的结果为 .
12、化简: ; .
13、计算(+)÷的结果是( )
A.- B. C.- D.
14、若恒成立,则 .
15、已知=5,则代数式的值为 .
16、如果a+b=2,那么的值是 .
17、如果,那么代数式的值是__________.
18、一种运算:规则是x※y=,根据此规则化简(m+1)※(m﹣1)的结果为 .
三、解答题
19、计算:
(1); (2).
20、(1)(1+)÷; (2)2+÷; (3)(a+)÷(1+).
21、先化简,再求值:
(1)(-)÷,其中a=+1.
(2)(1-)÷,其中a=-1.
(3)()· ,其中a=-.
22、先化简:÷(),再从-2<x<3的范围内选取一个你喜欢的x值代入求值.
23、已知a满足a2+2a-15=0,求-÷的值.
24、已知y=÷-x+3,试说明不论x为任何使原式有意义的值,y的值均不变.
25、分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式,例如:分式,是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.
例如,分式,是假分式,一个假分式可以化为一个整式与一个真分式的和.
例如:
(1)将假分式化为一个整数与一个真分式的和;
(2)利用上述方法解决问题:若是整数,且分式的值为正整数,求的值.
26、上课时老师在黑板上书写了一个分式的正确化简结果,随后用手掌盖住了一部分,形式如下:
(1)聪明的你请求出盖住部分化简后的结果
(2)当时,等于何值时,原分式的值为5
周末阶段复习提升训练卷5(分式的混合运算)-20-21苏科版八年级数学下册(答案)
一、选择题
1、化简的结果是
A. B. C. D.
【解析】原式,故选:.
2、化简的结果是
A. B. C. D.
【解析】原式.故选:.
3、化简的结果是
A. B. C. D.
【解析】;
故选:.
4、化简分式过程中开始出现错误的步骤是( )
A.① B.② C.③ D.④
解:∵
经过仔细比对,发现出错的步骤是题中所示②,分子相减时没有把第二个分子当作整体用括号括起来,
故选:B.
5、化简分式的结果是 ( A )
A.2 B. C. D.-2
6、若,则( )
A. B. C. D.
解:,
,
.
故选:.
7、如果,那么代数式的值为
A.9 B.6 C. D.
【解析】
,
,,原式, 故选:.
8、如图,在数轴上表示的值的点是( )
A.点 B.点 C.点 D.点
解:,
,
,
,
=1,
在数轴是对应的点是M,故选:C.
9、已知a、b为实数且满足a≠﹣1,b≠﹣1,设M=,N=,则下列两个结论( )
①ab=1时,M=N;ab>1时,M<N. ②若a+b=0,则M?N≤0.
A.①②都对 B.①对②错 C.①错②对 D.①②都错
【详解】∵M=,N= ,
∴①M﹣ N=﹣( ) =,
当ab=1时,M﹣N=0,∴M=N,
当ab>1时,2ab>2,∴2ab﹣2>0,
当a<0时,b<0,(a+1)(b+1)>0或(a+1)(b+1)<0,
∴M﹣N>0或M﹣N<0,
∴M>N或M<N; 故①错误;
②M?N=()?( )=.
∵a+b=0,∴原式==.
∵a≠﹣1,b≠﹣1,∴(a+1)2(b+1)2>0.
∵a+b=0,∴ab≤0,M?N≤0, 故②对.
故选:C.
二、填空题
10、计算的结果等于 .
【解析】.
故答案为:.
11、计算的结果为 .
【解析】原式
. 故答案为:.
12、化简: ; .
【解析】,
,
故答案为:、.
13、计算(+)÷的结果是( )
A.- B. C.- D.
[解析] 原式=·
=· =. 故选D
14、若恒成立,则 .
【解析】右边
,解,,,
故答案为4.
15、已知=5,则代数式的值为 .
【解析】∵=5,∴y﹣x=5xy,即x﹣y=﹣5xy.
∴ .
故答案为:.
16、如果a+b=2,那么的值是 .
【解析】原式
=a+b,
当a+b=2时,原式=2,故答案为:2.
17、如果,那么代数式的值是__________.
解:.
,,
.故答案为:.
18、一种运算:规则是x※y=,根据此规则化简(m+1)※(m﹣1)的结果为 .
【分析】根据所给规则列出算式,再通分,然后计算同分母的分式减法即可.
【解析】由题意得:(m+1)※(m﹣1),
,
,
,
=
故答案为:.
三、解答题
19、计算:
(1); (2).
【详解】(1)原式.
(2)原式
.
20、(1)(1+)÷; (2)2+÷; (3)(a+)÷(1+).
解:(1)(1+)÷=.
(2)2+÷=2-·=2-·
=2-=-==.
(3)原式=÷(+)=÷=·=a-1.
21、先化简,再求值:
(1)(-)÷,其中a=+1.
(2)(1-)÷,其中a=-1.
(3)()· ,其中a=-.
解:(1)原式=[-]·
=[-]·
=·
=.
将a=+1代入可得,原式==.
(2)(1-)÷=·=.
当a=-1时,原式===.
(3)原式=·=·=·=.
当a=-时,==-1.
22、先化简:÷(),再从-2<x<3的范围内选取一个你喜欢的x值代入求值.
解:原式=÷=·=.
由题意,可取x=2代入上式,得==4.(注意:x不能为0和±1)
23、已知a满足a2+2a-15=0,求-÷的值.
[解析] 对要求的式子进行计算,先进行因式分解,再把除法转化成乘法,然后进行约分,得到一个最简分式,最后把a2+2a-15=0进行配方,得到a+1的值,再把它整体代入即可求出答案.
解:-÷
=-·
=-=.
∵a2+2a-15=0,∴(a+1)2=16,
∴原式==.
24、已知y=÷-x+3,试说明不论x为任何使原式有意义的值,y的值均不变.
[解析] 先化简分式,再通过分析化简结果得出结论.
解:y=÷-x+3
=·-x+3
=x-x+3
=3.
由化简结果,可知y的值为常数3,与x的取值无关,
故不论x为任何使原式有意义的值,y的值均不变.
25、分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式,例如:分式,是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.
例如,分式,是假分式,一个假分式可以化为一个整式与一个真分式的和.
例如:
(1)将假分式化为一个整数与一个真分式的和;
(2)利用上述方法解决问题:若是整数,且分式的值为正整数,求的值.
【解析】(1)
(2)
分式的值为正整数
,
或或
或或
26、上课时老师在黑板上书写了一个分式的正确化简结果,随后用手掌盖住了一部分,形式如下:
(1)聪明的你请求出盖住部分化简后的结果
(2)当时,等于何值时,原分式的值为5
【解析】(1)
盖住部分化简后的结果为;
(2)时,原分式的值为5,即,
解得
经检验,是原方程的解.
所以当,时,原分式的值为5.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
