2020-2021学年北师大版数学七年级下册单元期末复习课件 第四章 三角形(共81张ppt)
文档属性
| 名称 | 2020-2021学年北师大版数学七年级下册单元期末复习课件 第四章 三角形(共81张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 09:31:42 | ||
图片预览









文档简介
(共81张PPT)
第四章 三角形
章末复习
第四章 三角形
章末复习
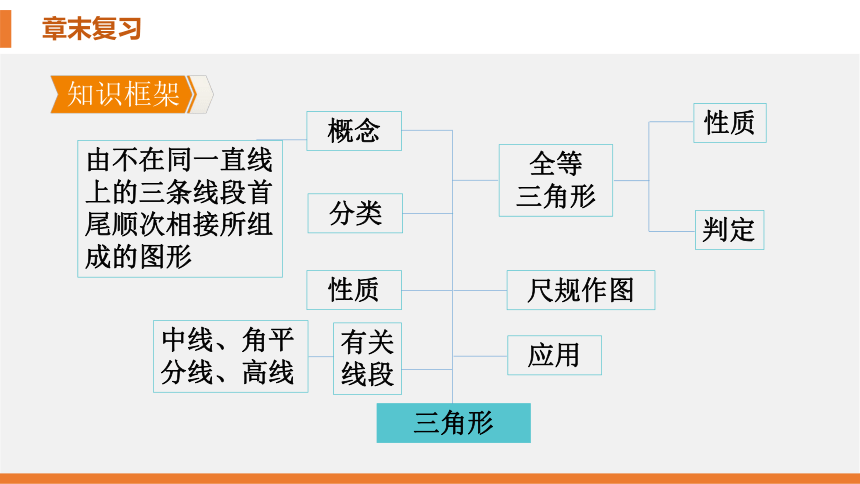
知识框架
归纳整合
素养提升
中考链接
知识框架
分类
三角形
全等
三角形
应用
判定
尺规作图
性质
有关线段
概念
性质
由不在同一直线上的三条线段首尾顺次相接所组成的图形
中线、角平分线、高线
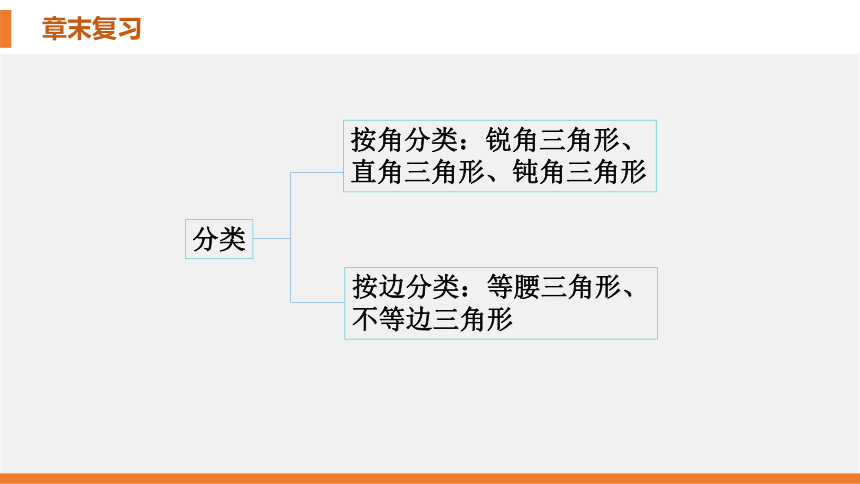
分类
按角分类:锐角三角形、
直角三角形、钝角三角形
按边分类:等腰三角形、
不等边三角形
三角形三个内角的和等于180°
三角形任意两边之和大于第三
边,
任意两边之差小于第三边
三角形具有稳定性
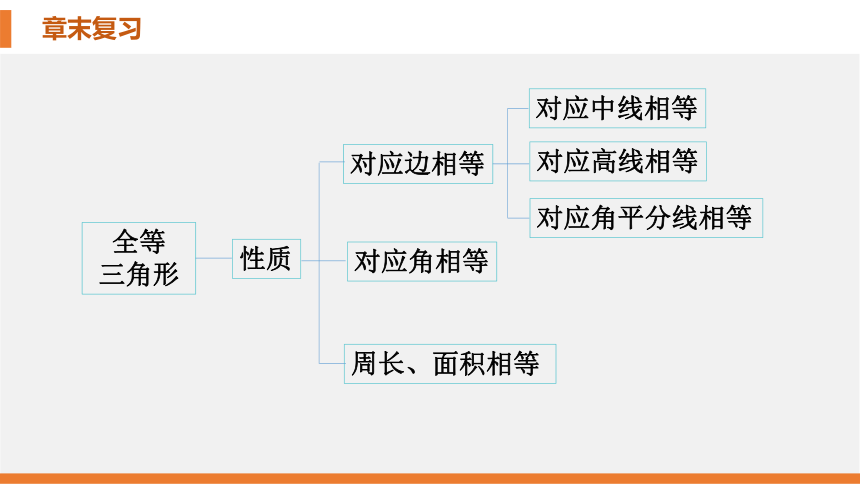
性质
对应边相等
对应角相等
周长、面积相等
性质
对应中线相等
对应高线相等
对应角平分线相等
全等
三角形
SSS
ASA或AAS
判定
SAS
应用
三角形稳定性的应用
用三角形全等测距离
【要点指导】三角形的三边关系:任意两边之和大于第三边;任
意两边之差小于第三边.利用三角形三边关系可以解决以下问题:
(1)判断三条线段能否构成三角形;
(2)求三角形第三边长的取值范围;
(3)确定三角形第三边的长,
并进一步求该三角形的周长等.
归纳整合
专题一
三角形三边关系的应用
例1
王伟准备用一段长30米的篱笆围成一个三角形形状的花圃.
已知第一条边长为a米,
由于受地势限制,
第二条边长只能比第一条边长的2倍多2米.
(1)请用含a的式子表示出第三条边长.
(2)第一条边长可以为8米吗?为什么?请说明理由.
(3)能否使围成的花圃是等腰三角形?若能,
说明你的围法;若不能,请说明理由.
分析
本题以三角形三边关系为载体,
主要考查了整式计算与三角形的有关边的知识的理解与运用,
在探究等腰三角形的形状时要注意分类讨论,构建方程分析与解决实际问题.
解:
(1)第一条边长为a米,
由题意得第二条边长为(2a+2)米,
所以第三条边长为30-a-(2a+2)=(28-3a)米.
(2)不可以为8米.
理由:因为a=8时,
2a+2=18,
28-3a=4,
又因为8+4<18,
不满足三角形三边之间的关系,
所以不能构成三角形.
(3)能围成等腰三角形.因为a>0,
所以当a=2a+2时,
此方程无解,
不能围成等腰三角形;当a=28-3a时,
解得a=7,
2a+2=16,
因为7+7<16,
不满足三角形三边之间的关系,
所以不能围成等腰三角形;当2a+2=28-3a时,解得
,因为
,此时满足三角形三边之间的关系,
所以存在三边长为
米,
米,
米的等腰三角形.
相关题1-1
已知△ABC的三边长都是整数,
且AB=2,
BC=6,
则△ABC的周长可能是(
).
A.14
B.16
C.18
D.20
A
[解析]
根据“三角形任意两边之和大于第三边”可知AC<8;根据“三角形任意两边之差小于第三边”可知AC>4,因此可以确定AC的取值范围,从而可以确定△ABC的周长的范围.
相关题1-2
已知等腰三角形ABC的两边长分别为2和3,
则等腰三角形ABC的周长为(
).
A.7
B.8
C.6或8
D.7或8
D
[解析]
2和3都可能是底边长,应分别考虑并判断是否可以组成三角形.
相关题1-3
设a,
b,
c是△ABC的三边长,
化简:|a-b-c|+|b-c-a|+
|c+a-b|.
解:
根据三角形的三边关系,得a所以a-b-c<0,b-c-a<0,c+a-b>0,
所以|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=a-b+3c.
【要点指导】三角形中的角度计算,
主要是指运用三角形三个内
角的和等于180°,
直角三角形的两个锐角互余,
以及三角形的角平分线、高线等知识进行有关角的度数的计算等.
专题二
与三角形有关的角度计算
例2
下列条件中,
不能判定△ABC为直角三角形的是(
).
A.∠A=2∠B=3∠C
B.2∠A=2∠B=∠C
C.∠A∶∠B∶∠C=3∶2∶1
D.∠A=
∠B=
∠C
A
分析
相关题2-1
如图4-Z-1,
△ABC的角平分线CD,
BE相交于点F,
∠A=90°,
EG∥BC,
且CG⊥EG于点G,
下列结论:①∠CEG
=2∠DCB;②∠DFB=
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.
其中正确结论的个数是(
).
图4-Z-1
C
③因为∠A=90°,所以∠ADC+∠ACD=90°.
因为CD平分∠ACB,
所以∠ACD=∠BCD,所以∠ADC+∠BCD=90°.
因为EG∥BC,且CG⊥EG,
所以∠GCB=90°,即∠GCD+∠BCD=90°,
所以∠ADC=∠GCD,故正确.
④无法证明CA平分∠BCG,故错误.
所以正确的为①②③.
相关题2-2
如图4-Z-2所示,
点A,
B,C,
D,
E,
F是平面上的六个点,
则∠A+∠B+∠C+∠D+∠E+∠F的度数是(
).
A.180°
B.360°
C.540°
D.720°
图4-Z-2
B
[解析]
如图,因为∠PGH=∠AGB=180°-∠A-∠B,
∠GHP=∠CHD=180°-∠C-∠D,
∠GPH=∠EPF=180°-∠E-∠F,
且∠PGH+∠GHP+∠GPH=180°,
所以540°-∠A-∠B-∠C-∠D-∠E-∠F=180°,
所以∠A+∠B+∠C+∠D+∠E+∠F=540°-180°=360°.
【要点指导】对于三角形中重要线段的问题,
应掌握重要线段所表示的含义,
例如与角有关的有三角形的角平分线和高线,
与此同时会涉及余角的相关知识,
同时还要注意三角形中平行线性质的运用等.
专题三
三角形中重要线段的应用
例3
如图4-Z-3,
在△ABC中,
E是BC边上一点,EC=2BE,
D是AC的中点,
设△ABC,
△ADF,
△BEF的面积分别为S
△ABC
,
S
△ADF
,
S
△BEF
,
且S
△ABC
=12,
则S
△ADF-S
△BEF= .
图4-Z-3
2
分析
由D是AC的中点且S
△ABC
=12,
可得S
△ABD
=
S
△ABC
=
×12=6;
同理由EC=2BE得BE=
BC,
可得S
△ABE
=
×12=4.
又S
△ABE-S△ABF
=S
△BEF
,
S
△ABD-S△ABF
=S
△ADF
,
等量代换可知S
△ADF-S△BEF
=2.
相关题3
如图4-Z-4,
AD为△ABC的中线,
BE为△ABD的中线.
(1)若∠ABE=15°,
∠BAD=35°,
求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,
则点E到BC边的距离为多少?
图4-Z-4
解:
(1)因为∠ABE=15°,∠BAD=35°,
所以∠BEA=180°-15°-35°=130°,
所以∠BED=180°-130°=50°.
(2)如图所示,EF是△BED中BD边上的高.
例4
如图4-Z-5,
BO,
CO分别平分∠ABC和∠ACB.
(1)若∠A=60°,
求∠O的度数;
(2)若∠A=100°或∠A=120°,
求∠O的度数;
(3)由(1)(2)你发现了什么规律?
写出你的结论,
并说明理由.
图4-Z-5
解:
如图4-Z-5,
因为BO,
CO分别平分∠ABC和∠ACB,
所以∠1=∠2,
∠3=∠4.
(1)因为∠A=60°,
所以∠1+∠2+∠3+∠4=120°,
所以∠1+∠4=60°,
所以∠O=120°.
(2)若∠A=100°,
则∠1+∠2+∠3+∠4=80°,
所以∠1+∠4=40°,
所以∠O=140°.
若∠A=120°,
则∠1+∠2+∠3+∠4=60°,
所以∠1+∠4=30°,
所以∠O
=150°.
图4-Z-5
(3)∠O=90°+
∠A.
理由:因为∠1+∠4=
∠ABC+
∠ACB=
(180°-∠A)
=90°-
∠A,
所以∠O=180°-(∠1+∠4)
=180°-
(
90°-
∠A)
=90°+
∠A.
图4-Z-5
相关题4
在△ABC中,
∠ACB>∠ABC,
AD平分∠BAC.
(1)如图4-Z-6①,
过点B作BE⊥射线AD于点E,则∠ABE与
(∠ACB+∠ABC)之间有何数量关系?请说明理由;
图4-Z-6
相关题4
在△ABC中,
∠ACB>∠ABC,
AD平分∠BAC.
(2)如图②,
过点C作CF⊥A
D
于
点
F
,
则
∠
D
C
F
,∠ACB,
ABC
之间又有怎样的数量关系?写出你的结论(不需说明理由);
图4-Z-6
相关题4
在△ABC中,
∠ACB>∠ABC,
AD平分∠BAC.
(3)
如图③,
过点A作AE⊥BC于点E,
则∠DAE与∠ACB,
∠ABC之间又有怎样的数量关系?写出你的结论(不需说明理由).
图4-Z-6
【要点指导】全等三角形的性质为证明线段(角)相等提供了依据.
三角形全等的判定方法有四种:“SSS”“SAS”“ASA”和“AAS”.
在具体问题中,
一般只直接给出一个或两个条件(有的甚至一个条件也不直接给出),
其余条件常隐含于条件或图形中,
因此找出这些隐含条件是解答问题的关键.
专题四
全等三角形的判定与性质的运用
例5
[衡阳中考]如图4-Z-7,
已知线段AC,
BD相交于点E,
AE=DE,
BE=CE.
(1)试说明:△ABE≌△DCE;
(2)当AB=5时,
求DC的长.
图4-Z-7
解:
(1)在△ABE和△DCE中,
因为AE=DE,
∠AEB=∠DEC,
BE=CE,
所以△ABE≌△DCE(SAS).
(2)因为△ABE≌△DCE,
所以AB=DC.
因为AB=5,
所以DC=5.
相关题5
[武汉中考]如图4-Z-8,点C,
F,
E,
B在一条直线上,∠CFD=
∠BEA,CE=BF,
DF=AE,
写出CD与AB之间的关系,
并说明理由.
图4-Z-8
[解析]由已知推出CF=BE,
根据“SAS”判定△AEB≌△DFC,
从而得出CD=AB,∠C=∠B,
根据平行线的判定得出CD∥AB.
解:CD∥AB,CD=AB,
理由:因为CE=BF,
所以CE-EF=BF-EF,即CF=BE.
在△DFC和△AEB中,
因为CF=BE,∠CFD=∠BEA,DF=AE,
所以△DFC≌△AEB(SAS),
所以CD=AB,∠C=∠B,
所以CD∥AB.
【要点指导】本类题以探究题、开放题为主,
通过“一题多变”与“一题多解”考查同学们的发散思维能力.
这种命题的方式是近年中考命题的一大亮点,
主要考查学生探索三角形全等的条件.
添加条件判定全等的题目,
首先要找到已具备的条件,
这些条件有些是题目明确给出的,
有些是题目隐含的,
然后依据三角形全等的判定方法找出还缺少的条件后进行添加.
但需注意添加条件时,
不能构成“SSA”的形式.
专题五
全等三角形开放探究型问题
例6
如图4-Z-9,
已知点B,
F,
C,
E在同一条直线上,
FB=CE,
AC=
DF.
能否由上面的已知条件说明AB∥DE?如果能,
请写出解答过程;如果不能,
请从下列三个条件中选择一个合适的条件,
添加到已知条件中,
使AB∥DE成立,
并给出理由.
供选择的三个条件(请从其中选择一个):①AB=DE;
②BC=EF;③∠ACB=∠DFE.
图4-Z-9
分析
解:
由上面的已知条件不能说明AB∥DE.
因为缺少说明△ABC和△DEF全等的条件.
有两种添加方法:
(1)添加
①AB=DE.
理由:因为FB=CE,
所以BC=EF.
又因为AC=DF,
AB=DE,所以△ABC≌△DEF,
所以∠B=∠E,
所以AB∥DE.
(2)添加
③∠ACB=∠DFE.
理由:因为FB=CE,
所以BC=EF.
又因为∠ACB=∠DFE
,
AC=DF,
所以△ABC≌△DEF,
所以∠B=∠E,
所以AB∥DE.
相关题6
如图4-Z-10,
△ABC的两条高AD,BE相交于点F,
请添加一个条件,
使得△ADC≌△BEC(不添加其他字母及辅助线),
你添加的条件是
.
答案不唯一,如AC=BC
图4-Z-10
[解析]
答案不唯一,如添加条件:AC=BC.
因为AD,BE是△ABC的两条高,
所以∠ADC=∠BEC=90°.
在△ADC和△BEC中,
因为∠ADC=∠BEC,∠C=∠C,AC=BC,
所以△ADC≌△BEC.
【要点指导】三角形作为初中阶段最基础、最重要的内容,
经常作为呈现知识、能力和数学思想的载体.在等腰三角形中常常涉及分类讨论思想.
素养提升
专题一
分类讨论思想
例1
已知等腰三角形的周长是24
cm.
(1)若腰长是底边长的2倍,
求腰长;
(2)已知其中一边长为6
cm,
求其他两边长.
分析
(1)可以通过设未知数来进行计算,
列出方程,
通过求方程的解得到答案,
其中体现了方程思想.
(2)要注意分两种情况考虑,
因为题目中没有说明这条边究竟是腰还是底边,
所以应该分成两种情况考虑:一种是6
cm长的边为腰,
另一种是6
cm长的边为底,
体现了数学中的分类讨论思想.
注意计算结果还要验证是否符合两边之和都大于第三边.
解:
(1)设底边长为x
cm,
则腰长为2x
cm,
根据题意,
得x+2x+2x=24,
解得x=4.8,
所以2x=2×4.8=9.6,
即腰长为9.6
cm.
(2)因为长为6
cm的边可能是腰,
也可能是底,
所以要分两种情况讨论.
当长为6
cm的边为腰时,
则底边长为24-6×2=12(cm).
因为6+6=12,
两边之和等于第三边,
所以长为6
cm的边为腰时不能组成三角形,
舍去;
当长为6
cm的边为底边时,
则腰长为(24-6)÷2=9(cm).
因为6+9>9,
所以可以组成三角形,
所以三角形的其他两边长均为9
cm
相关题1
已知a,
b,
c为△ABC的三边长,
b,
c满足(b-2)2
+|c-3|=0,
且a为方程|x-4|=2的解,
求△ABC的周长,
并判断△ABC的形状.
解:由(b-2)2+|c-3|=0可得b=2,c=3.
由|x-4|=2解得x=2或x=6,故a=2或a=6.
当a=6时,2+3<6,无法组成三角形,故舍去;
当a=2时,2+2>3,可以组成三角形,即△ABC的三边长分别为2,2,3,它的周长为7,它的形状是等腰三角形.
【要点指导】转化思想就是把复杂的问题转化为简单的问题,
把未知的问题转化为已知的问题来处理的一种思想,
这种思想是我们在解决问题时很重要的一种思想.
本章中最为常见的是把证明线段、角相等转化为证明三角形全等,
把测量长度、选址等实际问题转化为数学问题来解决.
专题二
转化思想的应用
例2
如图4-Z-11所示,
小强在河的岸边,
要测量河面上的一只船B与对岸码头A之间的距离,
他的做法如下:①在岸边确定一点C,
使点C与点A,
B在同一直线上;②在与AC垂直的方向作线段CD,取其中点O;
③作DF⊥CD,
使点F,
O,
A
在同一直线上;④在线段DF上找到一点
E,
使点E与点O,
B共线.
他说测出线段EF
的长就得到了船B与对岸码头A之间的距离.
他这样做有道理吗?为什么?
图4-Z-11
分析
解:小强的做法有道理.
理由:
因为AC⊥CD,
DF⊥CD,
所以∠C=∠D=90°.
又因为OC=OD,
∠AOC=∠FOD(对顶角相等),
所以△ACO≌△FDO(ASA),
所以OA=OF,
∠A=∠F(全等三角形的对应边相等,
对应角相等).
又因为∠AOB=∠FOE(对顶角相等),
所以△AOB≌△FOE(ASA),
所以EF=AB(全等三角形的对应边相等),
所以线段EF的长就是船B与对岸码头A之间的距离.
相关题2
如图4-Z-12所示,
要测量池宽AB,
可以从点A出发在地面上画一条线段AC,使AC⊥AB,
再从点C观测,在BA的延长线上找到一点B′,
使∠ACB′=∠ACB.这时量得的AB′的长度就是AB的长度.
请你说明其中的道理.
图4-Z-12
解:
在△ACB和△ACB′中,
因为∠CAB=∠CAB′=90°,AC=AC,∠ACB=∠ACB′,
所以△ACB≌△ACB′(ASA),
所以AB=AB′.
中考链接
母题1
(教材P86习题4.2第1题,
第2题)
1.下列每组数分别是三根小木棒的长度,
用它们能摆成三角形吗?实际摆一摆,
验证你的结论.
(1)3
cm,
4
cm,
5
cm;
(2)8
cm,
7
cm,
15
cm;
(3)13
cm,
12
cm,
20
cm;
(4)5
cm,
5
cm,
11
cm.
2.等腰三角形一边长9
cm,
另一边长4
cm,
它的第三边是多少?为什么?
考点:三角形的三边关系.
考情:主要考查三条线段能否构成三角形或求第三边长的取值.
策略:根据三角形任意两边之和大于第三边,
任意两边之差小于第三边,
确定未知边长的取值范围,
然后进一步求边长或周长.
链接1
[金华中考]下列各组数中,
不可能成为一个三角形三边长的是( ).
A.2,
3,
4
B.5,
7,
7
C.5,
6,
12
D.6,
8,
10
C
分析
因为5+6<12,
所以5,
6,
12不可能成为一个三角形的三边长.
故选C.
链接2
[自贡中考]已知三角形的两边长分别为1和4,
第三边长为整数,
则该三角形的周长为( ).
A.7
B.8
C.9
D.10
C
分析
设第三边长为x.
根据三角形的三边关系,
得4-1<x<4+1,即3<x<5.
因为x为整数,
所以x的值为4,
故三角形的周长为1+4+4=9.
故选C.
母题2
(教材P84随堂练习第2题)
一个三角形两个内角的度数分别如下,
这个三角形是什么三角形?
(1)30°和60°;
(2)40°和70°;
(3)50°和20°.
考点:三角形的内角和.
考情:主要考查三角形中角度的计算,
判断三角形的形状.
策略:根据“三角形三个内角的和等于180°”计算角的度数,
判断三角形的形状主要看三角形中最大角的度数,
最大角为钝角时是钝角三角形,最大角为直角时是直角三角形,
最大角为锐角时是锐角三角形.
链接3
[襄阳中考]如图4-Z-13,
AD是∠EAC的
平
分
线
,
A
D
∥
B
C
,∠B=30°,
则∠C的度数为( ).
A.50°
B.40°
C.30°
D.20°
C
图4-Z-13
分析
链接4
[绍兴中考]如图4-Z-14,
墙上钉着三根木条a,
b,c,
量得∠1
=70°,
∠2=100°,
那么木条a,
b所在直线所夹的锐角是( ).
A.5°
B.10°
C.30°
D.70°
B
图4-Z-14
分析
如图4-Z-15,
由对顶角相等可知∠3=∠2=100°,
所以木条a,
b所在直线所夹的锐角=180°-100°-70°=10°,
故选B.
图4-Z-15
链接5
[滨州中考]在△ABC中,
若∠A=30°,∠B=50°,
则∠C=
.
100°
分析
因为在△ABC中,
∠A=30°,
∠B=50°,
所以∠C=180°-30°-50°=100°.
母题3
(教材P104习题4.8第1题)
如图4-Z-16,
点E在AB上,
AC=AD,
∠CAB=∠DAB,
△ACE与△ADE全等吗?△ACB与△ADB呢?请说明理由.
图4-Z-16
考点:全等三角形的判定.
考情:主要考查利用“SAS”“ASA”“AAS”“SSS”判定三角形全等,
或说明线段相等、角相等.
策略:先根据已知条件或要说明的结论,
确定需要说明全等的三角形,
再根据三角形全等的判定方法,
确定所缺条件,
最后根据已知找所缺条件.
链接6
[成都中考]如图4-Z-17,
已知∠ABC=∠DCB,添
加
以
下
条
件
,
不
能
判
定△ABC≌△DCB的是( ).
A.∠A=∠D
B.∠ACB=∠DBC
C.AC=DB
D.AB=DC
C
图4-Z-17
分析
A项,
∠A=∠D,
∠ABC=∠DCB,BC=CB,
符合“AAS”,
即能推出△ABC≌△DCB,故本选项不符合题意;B项,
∠ABC=∠DCB,BC=CB,
∠ACB=∠DBC,
符合“ASA”,
即能推出△ABC≌△DCB,
故本选项不符合题意;C项,∠ABC=∠DCB,
AC=BD,
BC=CB,
不符合三角形全等的判定条件,
即不能推出△ABC≌△DCB,
故本选项符合题意;D项,
AB=DC,
∠ABC=∠DCB,BC=CB,
符合“SAS”,
即能推出△ABC≌△DCB,故本选项不符合题意.
链接7
[广州中考]如图4-Z-18,
AB与CD相交于点E,
AE=CE,
DE=BE.试说明:∠A=∠C.
图4-Z-18
解:
在△AED和△CEB中,
因为AE=CE,
∠AED=∠CEB,
DE=BE,
所以△AED≌△CEB(SAS),
所以∠A=∠C(全等三角形对应角相等).
谢
谢
观
看!
第四章 三角形
章末复习
第四章 三角形
章末复习
知识框架
归纳整合
素养提升
中考链接
知识框架
分类
三角形
全等
三角形
应用
判定
尺规作图
性质
有关线段
概念
性质
由不在同一直线上的三条线段首尾顺次相接所组成的图形
中线、角平分线、高线
分类
按角分类:锐角三角形、
直角三角形、钝角三角形
按边分类:等腰三角形、
不等边三角形
三角形三个内角的和等于180°
三角形任意两边之和大于第三
边,
任意两边之差小于第三边
三角形具有稳定性
性质
对应边相等
对应角相等
周长、面积相等
性质
对应中线相等
对应高线相等
对应角平分线相等
全等
三角形
SSS
ASA或AAS
判定
SAS
应用
三角形稳定性的应用
用三角形全等测距离
【要点指导】三角形的三边关系:任意两边之和大于第三边;任
意两边之差小于第三边.利用三角形三边关系可以解决以下问题:
(1)判断三条线段能否构成三角形;
(2)求三角形第三边长的取值范围;
(3)确定三角形第三边的长,
并进一步求该三角形的周长等.
归纳整合
专题一
三角形三边关系的应用
例1
王伟准备用一段长30米的篱笆围成一个三角形形状的花圃.
已知第一条边长为a米,
由于受地势限制,
第二条边长只能比第一条边长的2倍多2米.
(1)请用含a的式子表示出第三条边长.
(2)第一条边长可以为8米吗?为什么?请说明理由.
(3)能否使围成的花圃是等腰三角形?若能,
说明你的围法;若不能,请说明理由.
分析
本题以三角形三边关系为载体,
主要考查了整式计算与三角形的有关边的知识的理解与运用,
在探究等腰三角形的形状时要注意分类讨论,构建方程分析与解决实际问题.
解:
(1)第一条边长为a米,
由题意得第二条边长为(2a+2)米,
所以第三条边长为30-a-(2a+2)=(28-3a)米.
(2)不可以为8米.
理由:因为a=8时,
2a+2=18,
28-3a=4,
又因为8+4<18,
不满足三角形三边之间的关系,
所以不能构成三角形.
(3)能围成等腰三角形.因为a>0,
所以当a=2a+2时,
此方程无解,
不能围成等腰三角形;当a=28-3a时,
解得a=7,
2a+2=16,
因为7+7<16,
不满足三角形三边之间的关系,
所以不能围成等腰三角形;当2a+2=28-3a时,解得
,因为
,此时满足三角形三边之间的关系,
所以存在三边长为
米,
米,
米的等腰三角形.
相关题1-1
已知△ABC的三边长都是整数,
且AB=2,
BC=6,
则△ABC的周长可能是(
).
A.14
B.16
C.18
D.20
A
[解析]
根据“三角形任意两边之和大于第三边”可知AC<8;根据“三角形任意两边之差小于第三边”可知AC>4,因此可以确定AC的取值范围,从而可以确定△ABC的周长的范围.
相关题1-2
已知等腰三角形ABC的两边长分别为2和3,
则等腰三角形ABC的周长为(
).
A.7
B.8
C.6或8
D.7或8
D
[解析]
2和3都可能是底边长,应分别考虑并判断是否可以组成三角形.
相关题1-3
设a,
b,
c是△ABC的三边长,
化简:|a-b-c|+|b-c-a|+
|c+a-b|.
解:
根据三角形的三边关系,得a
所以|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=a-b+3c.
【要点指导】三角形中的角度计算,
主要是指运用三角形三个内
角的和等于180°,
直角三角形的两个锐角互余,
以及三角形的角平分线、高线等知识进行有关角的度数的计算等.
专题二
与三角形有关的角度计算
例2
下列条件中,
不能判定△ABC为直角三角形的是(
).
A.∠A=2∠B=3∠C
B.2∠A=2∠B=∠C
C.∠A∶∠B∶∠C=3∶2∶1
D.∠A=
∠B=
∠C
A
分析
相关题2-1
如图4-Z-1,
△ABC的角平分线CD,
BE相交于点F,
∠A=90°,
EG∥BC,
且CG⊥EG于点G,
下列结论:①∠CEG
=2∠DCB;②∠DFB=
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.
其中正确结论的个数是(
).
图4-Z-1
C
③因为∠A=90°,所以∠ADC+∠ACD=90°.
因为CD平分∠ACB,
所以∠ACD=∠BCD,所以∠ADC+∠BCD=90°.
因为EG∥BC,且CG⊥EG,
所以∠GCB=90°,即∠GCD+∠BCD=90°,
所以∠ADC=∠GCD,故正确.
④无法证明CA平分∠BCG,故错误.
所以正确的为①②③.
相关题2-2
如图4-Z-2所示,
点A,
B,C,
D,
E,
F是平面上的六个点,
则∠A+∠B+∠C+∠D+∠E+∠F的度数是(
).
A.180°
B.360°
C.540°
D.720°
图4-Z-2
B
[解析]
如图,因为∠PGH=∠AGB=180°-∠A-∠B,
∠GHP=∠CHD=180°-∠C-∠D,
∠GPH=∠EPF=180°-∠E-∠F,
且∠PGH+∠GHP+∠GPH=180°,
所以540°-∠A-∠B-∠C-∠D-∠E-∠F=180°,
所以∠A+∠B+∠C+∠D+∠E+∠F=540°-180°=360°.
【要点指导】对于三角形中重要线段的问题,
应掌握重要线段所表示的含义,
例如与角有关的有三角形的角平分线和高线,
与此同时会涉及余角的相关知识,
同时还要注意三角形中平行线性质的运用等.
专题三
三角形中重要线段的应用
例3
如图4-Z-3,
在△ABC中,
E是BC边上一点,EC=2BE,
D是AC的中点,
设△ABC,
△ADF,
△BEF的面积分别为S
△ABC
,
S
△ADF
,
S
△BEF
,
且S
△ABC
=12,
则S
△ADF-S
△BEF= .
图4-Z-3
2
分析
由D是AC的中点且S
△ABC
=12,
可得S
△ABD
=
S
△ABC
=
×12=6;
同理由EC=2BE得BE=
BC,
可得S
△ABE
=
×12=4.
又S
△ABE-S△ABF
=S
△BEF
,
S
△ABD-S△ABF
=S
△ADF
,
等量代换可知S
△ADF-S△BEF
=2.
相关题3
如图4-Z-4,
AD为△ABC的中线,
BE为△ABD的中线.
(1)若∠ABE=15°,
∠BAD=35°,
求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,
则点E到BC边的距离为多少?
图4-Z-4
解:
(1)因为∠ABE=15°,∠BAD=35°,
所以∠BEA=180°-15°-35°=130°,
所以∠BED=180°-130°=50°.
(2)如图所示,EF是△BED中BD边上的高.
例4
如图4-Z-5,
BO,
CO分别平分∠ABC和∠ACB.
(1)若∠A=60°,
求∠O的度数;
(2)若∠A=100°或∠A=120°,
求∠O的度数;
(3)由(1)(2)你发现了什么规律?
写出你的结论,
并说明理由.
图4-Z-5
解:
如图4-Z-5,
因为BO,
CO分别平分∠ABC和∠ACB,
所以∠1=∠2,
∠3=∠4.
(1)因为∠A=60°,
所以∠1+∠2+∠3+∠4=120°,
所以∠1+∠4=60°,
所以∠O=120°.
(2)若∠A=100°,
则∠1+∠2+∠3+∠4=80°,
所以∠1+∠4=40°,
所以∠O=140°.
若∠A=120°,
则∠1+∠2+∠3+∠4=60°,
所以∠1+∠4=30°,
所以∠O
=150°.
图4-Z-5
(3)∠O=90°+
∠A.
理由:因为∠1+∠4=
∠ABC+
∠ACB=
(180°-∠A)
=90°-
∠A,
所以∠O=180°-(∠1+∠4)
=180°-
(
90°-
∠A)
=90°+
∠A.
图4-Z-5
相关题4
在△ABC中,
∠ACB>∠ABC,
AD平分∠BAC.
(1)如图4-Z-6①,
过点B作BE⊥射线AD于点E,则∠ABE与
(∠ACB+∠ABC)之间有何数量关系?请说明理由;
图4-Z-6
相关题4
在△ABC中,
∠ACB>∠ABC,
AD平分∠BAC.
(2)如图②,
过点C作CF⊥A
D
于
点
F
,
则
∠
D
C
F
,∠ACB,
ABC
之间又有怎样的数量关系?写出你的结论(不需说明理由);
图4-Z-6
相关题4
在△ABC中,
∠ACB>∠ABC,
AD平分∠BAC.
(3)
如图③,
过点A作AE⊥BC于点E,
则∠DAE与∠ACB,
∠ABC之间又有怎样的数量关系?写出你的结论(不需说明理由).
图4-Z-6
【要点指导】全等三角形的性质为证明线段(角)相等提供了依据.
三角形全等的判定方法有四种:“SSS”“SAS”“ASA”和“AAS”.
在具体问题中,
一般只直接给出一个或两个条件(有的甚至一个条件也不直接给出),
其余条件常隐含于条件或图形中,
因此找出这些隐含条件是解答问题的关键.
专题四
全等三角形的判定与性质的运用
例5
[衡阳中考]如图4-Z-7,
已知线段AC,
BD相交于点E,
AE=DE,
BE=CE.
(1)试说明:△ABE≌△DCE;
(2)当AB=5时,
求DC的长.
图4-Z-7
解:
(1)在△ABE和△DCE中,
因为AE=DE,
∠AEB=∠DEC,
BE=CE,
所以△ABE≌△DCE(SAS).
(2)因为△ABE≌△DCE,
所以AB=DC.
因为AB=5,
所以DC=5.
相关题5
[武汉中考]如图4-Z-8,点C,
F,
E,
B在一条直线上,∠CFD=
∠BEA,CE=BF,
DF=AE,
写出CD与AB之间的关系,
并说明理由.
图4-Z-8
[解析]由已知推出CF=BE,
根据“SAS”判定△AEB≌△DFC,
从而得出CD=AB,∠C=∠B,
根据平行线的判定得出CD∥AB.
解:CD∥AB,CD=AB,
理由:因为CE=BF,
所以CE-EF=BF-EF,即CF=BE.
在△DFC和△AEB中,
因为CF=BE,∠CFD=∠BEA,DF=AE,
所以△DFC≌△AEB(SAS),
所以CD=AB,∠C=∠B,
所以CD∥AB.
【要点指导】本类题以探究题、开放题为主,
通过“一题多变”与“一题多解”考查同学们的发散思维能力.
这种命题的方式是近年中考命题的一大亮点,
主要考查学生探索三角形全等的条件.
添加条件判定全等的题目,
首先要找到已具备的条件,
这些条件有些是题目明确给出的,
有些是题目隐含的,
然后依据三角形全等的判定方法找出还缺少的条件后进行添加.
但需注意添加条件时,
不能构成“SSA”的形式.
专题五
全等三角形开放探究型问题
例6
如图4-Z-9,
已知点B,
F,
C,
E在同一条直线上,
FB=CE,
AC=
DF.
能否由上面的已知条件说明AB∥DE?如果能,
请写出解答过程;如果不能,
请从下列三个条件中选择一个合适的条件,
添加到已知条件中,
使AB∥DE成立,
并给出理由.
供选择的三个条件(请从其中选择一个):①AB=DE;
②BC=EF;③∠ACB=∠DFE.
图4-Z-9
分析
解:
由上面的已知条件不能说明AB∥DE.
因为缺少说明△ABC和△DEF全等的条件.
有两种添加方法:
(1)添加
①AB=DE.
理由:因为FB=CE,
所以BC=EF.
又因为AC=DF,
AB=DE,所以△ABC≌△DEF,
所以∠B=∠E,
所以AB∥DE.
(2)添加
③∠ACB=∠DFE.
理由:因为FB=CE,
所以BC=EF.
又因为∠ACB=∠DFE
,
AC=DF,
所以△ABC≌△DEF,
所以∠B=∠E,
所以AB∥DE.
相关题6
如图4-Z-10,
△ABC的两条高AD,BE相交于点F,
请添加一个条件,
使得△ADC≌△BEC(不添加其他字母及辅助线),
你添加的条件是
.
答案不唯一,如AC=BC
图4-Z-10
[解析]
答案不唯一,如添加条件:AC=BC.
因为AD,BE是△ABC的两条高,
所以∠ADC=∠BEC=90°.
在△ADC和△BEC中,
因为∠ADC=∠BEC,∠C=∠C,AC=BC,
所以△ADC≌△BEC.
【要点指导】三角形作为初中阶段最基础、最重要的内容,
经常作为呈现知识、能力和数学思想的载体.在等腰三角形中常常涉及分类讨论思想.
素养提升
专题一
分类讨论思想
例1
已知等腰三角形的周长是24
cm.
(1)若腰长是底边长的2倍,
求腰长;
(2)已知其中一边长为6
cm,
求其他两边长.
分析
(1)可以通过设未知数来进行计算,
列出方程,
通过求方程的解得到答案,
其中体现了方程思想.
(2)要注意分两种情况考虑,
因为题目中没有说明这条边究竟是腰还是底边,
所以应该分成两种情况考虑:一种是6
cm长的边为腰,
另一种是6
cm长的边为底,
体现了数学中的分类讨论思想.
注意计算结果还要验证是否符合两边之和都大于第三边.
解:
(1)设底边长为x
cm,
则腰长为2x
cm,
根据题意,
得x+2x+2x=24,
解得x=4.8,
所以2x=2×4.8=9.6,
即腰长为9.6
cm.
(2)因为长为6
cm的边可能是腰,
也可能是底,
所以要分两种情况讨论.
当长为6
cm的边为腰时,
则底边长为24-6×2=12(cm).
因为6+6=12,
两边之和等于第三边,
所以长为6
cm的边为腰时不能组成三角形,
舍去;
当长为6
cm的边为底边时,
则腰长为(24-6)÷2=9(cm).
因为6+9>9,
所以可以组成三角形,
所以三角形的其他两边长均为9
cm
相关题1
已知a,
b,
c为△ABC的三边长,
b,
c满足(b-2)2
+|c-3|=0,
且a为方程|x-4|=2的解,
求△ABC的周长,
并判断△ABC的形状.
解:由(b-2)2+|c-3|=0可得b=2,c=3.
由|x-4|=2解得x=2或x=6,故a=2或a=6.
当a=6时,2+3<6,无法组成三角形,故舍去;
当a=2时,2+2>3,可以组成三角形,即△ABC的三边长分别为2,2,3,它的周长为7,它的形状是等腰三角形.
【要点指导】转化思想就是把复杂的问题转化为简单的问题,
把未知的问题转化为已知的问题来处理的一种思想,
这种思想是我们在解决问题时很重要的一种思想.
本章中最为常见的是把证明线段、角相等转化为证明三角形全等,
把测量长度、选址等实际问题转化为数学问题来解决.
专题二
转化思想的应用
例2
如图4-Z-11所示,
小强在河的岸边,
要测量河面上的一只船B与对岸码头A之间的距离,
他的做法如下:①在岸边确定一点C,
使点C与点A,
B在同一直线上;②在与AC垂直的方向作线段CD,取其中点O;
③作DF⊥CD,
使点F,
O,
A
在同一直线上;④在线段DF上找到一点
E,
使点E与点O,
B共线.
他说测出线段EF
的长就得到了船B与对岸码头A之间的距离.
他这样做有道理吗?为什么?
图4-Z-11
分析
解:小强的做法有道理.
理由:
因为AC⊥CD,
DF⊥CD,
所以∠C=∠D=90°.
又因为OC=OD,
∠AOC=∠FOD(对顶角相等),
所以△ACO≌△FDO(ASA),
所以OA=OF,
∠A=∠F(全等三角形的对应边相等,
对应角相等).
又因为∠AOB=∠FOE(对顶角相等),
所以△AOB≌△FOE(ASA),
所以EF=AB(全等三角形的对应边相等),
所以线段EF的长就是船B与对岸码头A之间的距离.
相关题2
如图4-Z-12所示,
要测量池宽AB,
可以从点A出发在地面上画一条线段AC,使AC⊥AB,
再从点C观测,在BA的延长线上找到一点B′,
使∠ACB′=∠ACB.这时量得的AB′的长度就是AB的长度.
请你说明其中的道理.
图4-Z-12
解:
在△ACB和△ACB′中,
因为∠CAB=∠CAB′=90°,AC=AC,∠ACB=∠ACB′,
所以△ACB≌△ACB′(ASA),
所以AB=AB′.
中考链接
母题1
(教材P86习题4.2第1题,
第2题)
1.下列每组数分别是三根小木棒的长度,
用它们能摆成三角形吗?实际摆一摆,
验证你的结论.
(1)3
cm,
4
cm,
5
cm;
(2)8
cm,
7
cm,
15
cm;
(3)13
cm,
12
cm,
20
cm;
(4)5
cm,
5
cm,
11
cm.
2.等腰三角形一边长9
cm,
另一边长4
cm,
它的第三边是多少?为什么?
考点:三角形的三边关系.
考情:主要考查三条线段能否构成三角形或求第三边长的取值.
策略:根据三角形任意两边之和大于第三边,
任意两边之差小于第三边,
确定未知边长的取值范围,
然后进一步求边长或周长.
链接1
[金华中考]下列各组数中,
不可能成为一个三角形三边长的是( ).
A.2,
3,
4
B.5,
7,
7
C.5,
6,
12
D.6,
8,
10
C
分析
因为5+6<12,
所以5,
6,
12不可能成为一个三角形的三边长.
故选C.
链接2
[自贡中考]已知三角形的两边长分别为1和4,
第三边长为整数,
则该三角形的周长为( ).
A.7
B.8
C.9
D.10
C
分析
设第三边长为x.
根据三角形的三边关系,
得4-1<x<4+1,即3<x<5.
因为x为整数,
所以x的值为4,
故三角形的周长为1+4+4=9.
故选C.
母题2
(教材P84随堂练习第2题)
一个三角形两个内角的度数分别如下,
这个三角形是什么三角形?
(1)30°和60°;
(2)40°和70°;
(3)50°和20°.
考点:三角形的内角和.
考情:主要考查三角形中角度的计算,
判断三角形的形状.
策略:根据“三角形三个内角的和等于180°”计算角的度数,
判断三角形的形状主要看三角形中最大角的度数,
最大角为钝角时是钝角三角形,最大角为直角时是直角三角形,
最大角为锐角时是锐角三角形.
链接3
[襄阳中考]如图4-Z-13,
AD是∠EAC的
平
分
线
,
A
D
∥
B
C
,∠B=30°,
则∠C的度数为( ).
A.50°
B.40°
C.30°
D.20°
C
图4-Z-13
分析
链接4
[绍兴中考]如图4-Z-14,
墙上钉着三根木条a,
b,c,
量得∠1
=70°,
∠2=100°,
那么木条a,
b所在直线所夹的锐角是( ).
A.5°
B.10°
C.30°
D.70°
B
图4-Z-14
分析
如图4-Z-15,
由对顶角相等可知∠3=∠2=100°,
所以木条a,
b所在直线所夹的锐角=180°-100°-70°=10°,
故选B.
图4-Z-15
链接5
[滨州中考]在△ABC中,
若∠A=30°,∠B=50°,
则∠C=
.
100°
分析
因为在△ABC中,
∠A=30°,
∠B=50°,
所以∠C=180°-30°-50°=100°.
母题3
(教材P104习题4.8第1题)
如图4-Z-16,
点E在AB上,
AC=AD,
∠CAB=∠DAB,
△ACE与△ADE全等吗?△ACB与△ADB呢?请说明理由.
图4-Z-16
考点:全等三角形的判定.
考情:主要考查利用“SAS”“ASA”“AAS”“SSS”判定三角形全等,
或说明线段相等、角相等.
策略:先根据已知条件或要说明的结论,
确定需要说明全等的三角形,
再根据三角形全等的判定方法,
确定所缺条件,
最后根据已知找所缺条件.
链接6
[成都中考]如图4-Z-17,
已知∠ABC=∠DCB,添
加
以
下
条
件
,
不
能
判
定△ABC≌△DCB的是( ).
A.∠A=∠D
B.∠ACB=∠DBC
C.AC=DB
D.AB=DC
C
图4-Z-17
分析
A项,
∠A=∠D,
∠ABC=∠DCB,BC=CB,
符合“AAS”,
即能推出△ABC≌△DCB,故本选项不符合题意;B项,
∠ABC=∠DCB,BC=CB,
∠ACB=∠DBC,
符合“ASA”,
即能推出△ABC≌△DCB,
故本选项不符合题意;C项,∠ABC=∠DCB,
AC=BD,
BC=CB,
不符合三角形全等的判定条件,
即不能推出△ABC≌△DCB,
故本选项符合题意;D项,
AB=DC,
∠ABC=∠DCB,BC=CB,
符合“SAS”,
即能推出△ABC≌△DCB,故本选项不符合题意.
链接7
[广州中考]如图4-Z-18,
AB与CD相交于点E,
AE=CE,
DE=BE.试说明:∠A=∠C.
图4-Z-18
解:
在△AED和△CEB中,
因为AE=CE,
∠AED=∠CEB,
DE=BE,
所以△AED≌△CEB(SAS),
所以∠A=∠C(全等三角形对应角相等).
谢
谢
观
看!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
