2020-2021学年北师大版数学七年级下册单元期末复习课件 第五章 生活中的轴对称(共69张ppt)
文档属性
| 名称 | 2020-2021学年北师大版数学七年级下册单元期末复习课件 第五章 生活中的轴对称(共69张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览






文档简介
(共69张PPT)
第五章 生活中的轴对称
章末复习
第五章 生活中的轴对称
章末复习
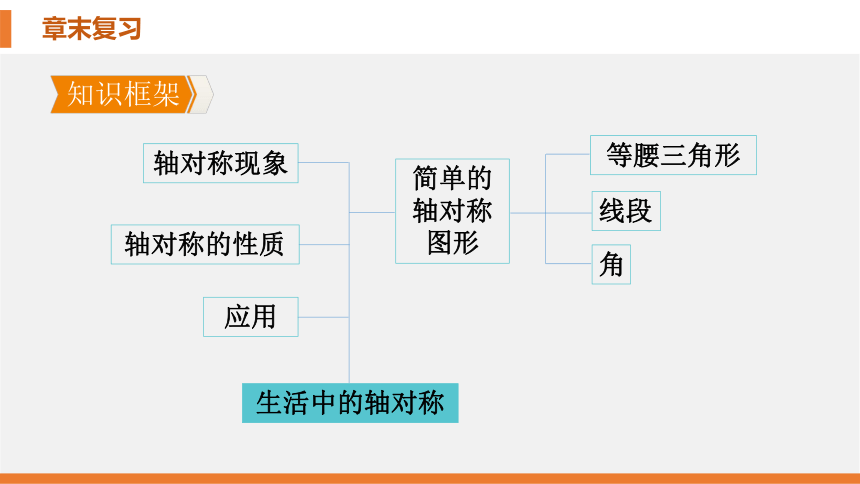
知识框架
归纳整合
素养提升
中考链接
知识框架
轴对称的性质
生活中的轴对称
简单的轴对称
图形
角
等腰三角形
轴对称现象
应用
线段
轴对称现象
轴对称图形
两个图形成轴对称
轴对称的性质
对应点所连的线段
被对称轴垂直平分
对应线段相等、
对应角相等
作对称点、对称线段
作轴对称图形
应用
设计轴对称图案
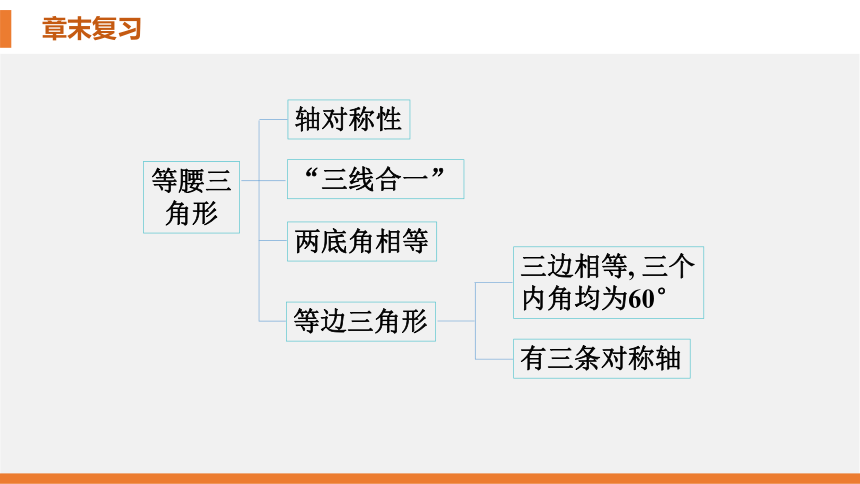
轴对称性
“三线合一”
等腰三角形
两底角相等
等边三角形
三边相等,
三个
内角均为60°
有三条对称轴
线段
轴对称性
线段垂直平分线的性质
角
轴对称性
角平分线的性质
【要点指导】轴对称图形的识别:方法1,
动手折叠,
再看折痕所在
直线两旁的两部分能不能“完全重合”;方法2,
找对应点,
也可以从反面入手,
即先找“对称轴”,
再看是不是每一个点都有关于这条直线对称的对应点,
如果有一个点没有对应点,
那么这个图形就不是轴对称图形.
归纳整合
专题一
轴对称图形的识别
例1
在下面由冬季奥运会比赛项目图标组成的四个图形中,
可以看作是轴对称图形的是(
).
图5-Z-1
D
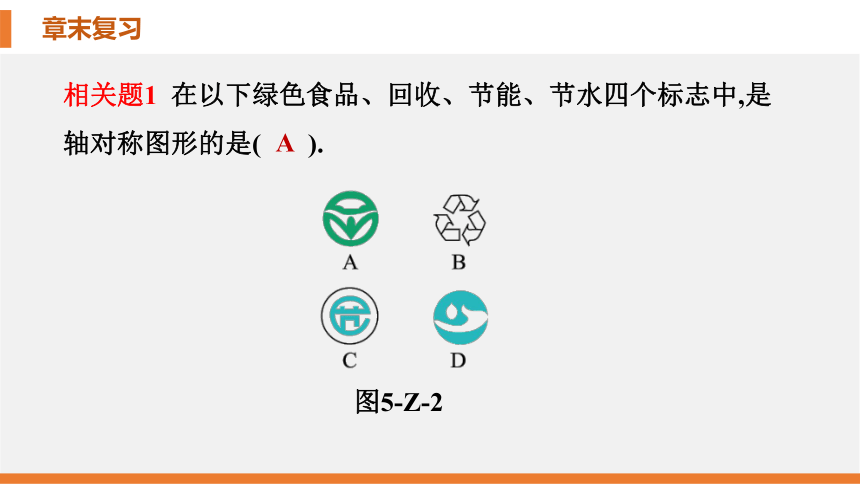
相关题1
在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是(
).
A
图5-Z-2
【要点指导】与轴对称有关的作图题能有效地考查同学们的动手操作能力和空间想象能力,
一直是考试的热点.
考查的基本题型有:(1)画轴对称图形;(2)确定对应点;(3)确定对称轴.
作图的关键是作对称轴的垂线段,
确定原图形上的点关于对称轴的对应点.
专题二
与轴对称有关的作图问题及其应用
例2
如图5-Z-3所示,
已知△ABC和直线MN.
求作:△A′B′C′,
使
△A′B′C′和△ABC关于直线MN对称.(不要求写作法,
只保留作图痕迹)
图5-Z-3
分析
分别过点A,
B,
C作MN的垂线段并延长到点A′,
B′,
C′,
使点A′,B′,
C′到MN的垂线段的长度分别等于点A,
B,
C到MN的垂线段的长度,
连接A′B′,
A′C′,
B′C′,
即得△A′B′C′.
解:
如图5-Z-3所示.
图5-Z-3
相关题2
[绥化中考]如图5-Z-4,
在8×8的正方形网格中,
每个小正方形的边长都是1.已知△ABC的三个顶点都在格点上,
画出△ABC关于直线l对称的△A1
B1
C1
.
图5-Z-4
解:如图所示.
【要点指导】关于线段垂直平分线,
关键是要把握它的性质及与它有关的基本作图的步骤、技巧.借助“线段垂直平分线上的点到这条线段两端点的距离相等”,
实现相关线段的转移.
专题三
线段垂直平分线的性质及应用
例3
[遂宁中考]如图5-Z-5,
在△ABC中,
AC=4
cm,
线段AB的垂直平分线交AC于点N.
若△BCN的周长是7
cm,
则BC的长为(
).
A.1
cm
B.2
cm
C.3
cm
D.4
cm
图5-Z-5,
C
分析
因为MN是线段AB的垂直平分线,
所以AN=BN.
又因为△BCN的周长是7
cm,
所以AN+NC+BC=BN+NC+BC=7
cm,
而AN+NC=AC,
故AC+BC=7
cm.
因为AC=4
cm,
所以BC=7-4=3(cm).
相关题3
如图5-Z-6,
在△ABC中,分别以点A和点B为圆心,大于
AB的长为半径画弧,两弧相交于点M,
N,
作直线MN,
交BC于点D,
连接AD.
若△ADC的周长为10,AB=7,
则△ABC的周长为
(
).
A.7
B.14
C.17
D.20
图5-Z-6
C
[解析]由作图可知MN是线段AB的垂直平分线,得AD=BD,
所以△ABC的周长为AC+BC+AB=AC+CD+AD+AB=10+7=17.
故选C.
【要点指导】角是轴对称图形,
对称轴是角平分线所在的直线;角
平分线分得的两个角相等,
角平分线上的点到这个角的两边的距离相等,角平分线可以看作是到角两边距离相等的所有点的集合.
专题四
角平分线性质的运用
例4
如图5-Z-7,
在直角三角形ABC中,∠A=90°,
∠ABC的平分线BD交AC于点D,
AD=3,BC=10,
则△BDC的面积是 .
图5-Z-7
15
分析
过点D作DE⊥BC于点E,
则DE=AD=3.
又因为BC=10,
所以S
△BDC
=
BC·DE=
×10×3=15.
相关题4
如
图5
-Z
-8
,
OP
平分∠MON,
PA⊥ON于点A,
Q是射线OM上的一个动点.若PA=3,
则PQ的长不可能为(
).
A.1
B.3
C.5
D.7
图5
-Z
-8
A
[解析]如图,过点P作PQ⊥OM,垂足为Q,则此时PQ的长最小.
因为OP平分∠MON,PA⊥ON,PQ⊥OM,
所以PQ=PA=3,即PQ的最小值是3,不可能取1.
故选A.
【要点指导】折叠后的图形与折叠前的图形关于折痕所在的直线成轴对称,
即折叠前后的图形全等,
常利用这一点求线段的长或角的度数.
专题五
折叠中的对称
例5
如图5-Z-9所示,
把直角三角形纸片沿过顶点B的直线(BE交CA于点E)折叠,
直角顶点C落在斜边AB上,
如果折叠后得等腰三角形EBA,
那么下列结论:①∠ABC=60°;②点C与AB的中点重合;③点E到AB的距离等于CE的长.
其中正确的个数是(
).
A.0
B.1
C.2
D.3
图5-Z-9
D
分析
因为把直角三角形纸片沿过顶点B的直线(BE交CA于点E)折叠,
直角顶点C落在斜边AB上,
折叠后得等腰三角形EBA,
所以∠A=∠EBA,
∠CBE=∠EBA,所以∠A=∠CBE=∠EBA.
因为∠C=90°,所以∠A+∠CBE+∠EBA=90°,
所以∠A=∠CBE=∠EBA=30°,
所以∠ABC=60°,
故①正确.
因为∠A=∠EBA,
∠EDB=90°,所以AD=BD,
故②正确.
因为∠C=∠EDB=90°,
∠CBE=∠EBD=30°,
所以CE=DE(角平分线上的点到角两边的距离相等),
所以点E到AB的距离等于CE的长,
故③正确.
综上,
正确的有3个.
相关题5
[乌鲁木齐中考]如图5-Z-10,
△ABC的面积等于6,
边AC的长为3,
现将△ABC沿AB所在直线翻折,
使点C落在直线AD上的点C'处,
点P在直线AD上,
则线段BP的长不可能是(
).
A.3
B.4
C.5
D.6
A
图4-Z-10
【要点指导】等腰(等边)三角形是轴对称图形,
其对称轴是顶角平分线(或底边上的高或底边上的中线)所在的直线.
等腰三角形有以下性质:等腰三角形的两个底角相等(简写成“等边对等角”);等腰三角形的顶角平分线、底边上的中线、底边上的高重合(简称“三线合一”);等腰三角形的两底角的平分线相等;等腰三角形底边的垂直平分线上的点到两条腰的距离相等.
等边三角形是特殊的等腰三角形,
以上性质对等边三角形都适用.
专题六
等腰(等边)三角形性质的应用
例6
如图5-Z-11,
在直角三角形ABC中,∠C=90°,
直线BD交AC于点D,
把直角三角形沿着直线BD翻折,
点C恰好落在斜边AB上.
如果△ABD是等腰三角形,
那么∠A等于(
).
A.60°
B.45°
C.30°
D.22.5°
图5-Z-11
C
分析
根据题意,
得∠CBD=∠ABD.
因为△ABD是等腰三角形,
所以∠ABD=∠A,
所以∠ABD=∠A=∠CBD.
又因为∠C=90°,
所以∠A+∠ABC=3∠A=90°,
解得∠A=30°.
相关题6
[
黔
西
南
州
中
考
]
如
图5-Z-12,
已知△ABC是等边三角形,
点B,
C,
D,E在同一条直线上,
且CG=CD,
DF=DE,
则∠E=
°
.
15
图5-Z-12
【要点指导】线段的垂直平分线和角平分线性质的应用体现了数学建模思想,
解决这类题目的关键是:首先要理解题意,
把生活中的情景问题转化为数学模型来考虑;其次是用学过的知识来分析建立数学模型,
把复杂的问题分解成一个个我们熟悉的数学知识点来解决,
“分析——构建模型——设计方案——论证方案——得出结论”是解决此类题目的五个步骤.
素养提升
专题一
数学建模思想
例1
如图5-Z-13,
公路l同侧有A,
B两个工厂,
现要在公路上建一仓库.
(1)若要使仓库到A,
B两工厂的距离相等,
仓库应建在何处?
(2)若要使仓库到A,
B两工厂的距离之和最短,
仓库应建在何处?
图5-Z-13
分析
(1)由线段垂直平分线的性质可知仓库应建在线段AB的垂直平分线上.
又因为仓库在公路上,
所以线段AB的垂直平分线与公路l的交点即为仓库应建的地点.
(2)如果A,
B两点在直线l的两侧,
那么连接AB与l的交点即为所求,
由于现在A,
B两点在l的同侧,
因此可考虑作点A(或点B)关于l的对称点C,由轴对称的性质可知,
直线l上任意一点到点A,
C的距离相等,
这样就把直线l上一点到点A的距离转化为到点C的距离,
因此连接BC与l的交点即为所求.
解:
(1)如图5-Z-14①,
连接AB,
作AB的垂直平分线交直线l于点P,
点P就是所要求作的仓库的位置.
(2)如图5-Z-14②,
作点A关于直线l的对称点C,
连接BC交直线l于点D,点D就是所要求作的仓库的位置.
图5-Z-14
相关题1-1
如图5-Z-15,
需要在高速公路旁边修建一个飞机场,
使飞机场到A,
B两个城市的距离之和最小,
请作出机场的位置.
图5-Z-15
[解析]
利用轴对称的性质可作点A关于公路的对称点A′,连接A′B,与公路的交点就是飞机场的位置.
解:点P就是飞机场的位置.
相关题1-2
已知直线l及其两侧两点A,B,
如图5-Z-16.
(1)在直线l上作一点P,
使PA=PB;
(2)在直线l上作一点Q,
使l平分∠AQB.
(以上两小题保留作图痕迹,
标出必要的字母,
不要求写作法)
图5-Z-16
解:(1)作线段AB的垂直平分线与直线l的交点即为所求,图略.
(2)作点A关于直线l的对称点A′,连接BA′并延长交l于点Q,点Q即为所求,图略.
【要点指导】等腰三角形是一种特殊而又十分重要的三角形,它的边、角的特殊性在处理许多几何问题中起着关键的作用.
求解与等腰三角形的边、角有关的计算题时,
在条件不明确的情况下,
应根据题目的特点分类讨论.
专题二
分类讨论思想
例2
已知一个等腰三角形两个内角的度数之比为1∶4,
则这个等腰三角形顶角的度数为(
).
A.20°
B.120°
C.20°或120°
D.36°
C
分析
应分等腰三角形顶角与底角的度数之比为1∶4和等腰三角形底角与顶角的度数之比为1∶4两种情况讨论.
具体过程如下:设等腰三角形的顶角为α.
(1)若等腰三角形顶角与底角的度数之比为1∶4,
则α+4α+4α=180°,
解得α=20°;
(2)若等腰三角形底角与顶角的度数之比为1∶4,
则α+
α+
α=180°,
解得α=120°.
综上,
这个等腰三角形顶角的度数为20°或120°.
故选C.
相关题2
已知等腰三角形一腰上的中线把该三角形的周长分成18
cm和21
cm的两部分,
求该等腰三角形的各边长.
[解析]
画草图如图,腰AC上的中线BD把△ABC的周长分成18
cm和21
cm的两部分,列方程可解决问题.
中考链接
母题1
(教材P117习题5.1第1题)
观察下面的图形,
哪些图形是轴对称图形?如果是轴对称图形,
请画出对称轴.
图5-Z-17
考点:轴对称图形.
考情:主要考查轴对称图形及对称轴数量的判断,
多在选择题中出现.
策略:判断一个图形是不是轴对称图形,
可采用折叠的方法,
看折痕所在直线两边的部分是否能够重合.
若能找到一条直线,
使该图形沿着这条直线折叠,
直线两旁的部分互相重合,
则这个图形就是轴对称图形,
这条直线就是对称轴.
链接1
[天津中考]在一些美术字中,
有的汉字是轴对称图形.
下面4个汉字中,
可以看作是轴对称图形的是(
).
A
图5-Z-18
链接2
[广州中考]如图5-Z-19所示的五角星是轴对称图形,
它的对称轴共有(
).
A.1条 B.3条
C.5条 D.无数条
C
图5-Z-19
母题2
(教材P122随堂练习第3题)
如图5-Z-20,
在下面的等腰三角形中,
∠A是顶角,
分别求出它们的底角的度数.
图5-Z-20
考点:等腰三角形.
考情:主要考查等腰三角形的周长、边长及角度的计算.
策略:(1)等腰三角形中求角度时,
一定要分清顶角和底角.
若已知等腰三角形的顶角为x°,
则底角为
;若底角为x°,
则顶角为(180-2x)°.
(2)计算角的度数时,
往往结合三角形的内角和为180°,
运用方程思想计算.
链接3
[呼伦贝尔中考]如图5-Z-21,
在△ABC中,
AB=AC,过点A作AD∥BC.
若∠1=70°,则∠BAC的度数为(
).
A.40°
B.30°
C.70°
D.50°
A
图5-Z-21
分析
因为AD∥BC,
所以∠C=∠1=70°.
因为AB=AC,
所以∠B=∠C=70°,
所以∠BAC=180°-∠B-∠C=40°.
故选A.
链接4
[湖州中考]如图5-Z-22所示,
AD,
CE分别是△ABC的中线和角平分线.
若AB=AC,
∠CAD=20°,则∠ACE的度数是(
).
A.20°
B.35°
C.40°
D.70°
B
图5-Z-22
分析
因为AD是△ABC的中线,
AB=AC,∠CAD=20°,
所以∠CAB=2∠CAD=40°,
∠B=∠ACB=
(180°-∠CAB)=70°.
因为CE是△ABC的角平分线,
所以∠ACE=
∠ACB=35°.
母题3
(教材P124习题5.4第1题)
画一条线段AB,
利用尺规求作它的四等分点.
考点:线段垂直平分线、尺规作图.
考情:利用尺规作线段的垂直平分线.
策略:找线段的中点实际就是作线段的垂直平分线.
作四等分点,
就是连续作线段的垂直平分线.
线段的垂直平分线既垂直于线段又平分线段,作图要严格按照尺规作图的步骤,
保留作图痕迹.
链接5
[陕西中考]如图5-Z-23,
已知△ABC,请用尺规过点A作一条直线,
使其将△ABC分成面积相等的两部分.(保留作图痕迹,
不写作法)
图5-Z-23
解:
(1)分别以点B和C为圆心,
以大于
BC的长为半径画弧;
(2)连接两弧交点,
所得直线与BC交于点D,
作直线AD,
则直线AD就是所求作的直线,
如图5-Z-24.
图5-Z-24
母题4
(教材P133复习题第11题)
以虚线为对称轴画出图的另一半:
图5-Z-25
考点:
轴对称的性质.
考情:
主要考查轴对称作图.
策略:
作轴对称图形的关键是找准图形中的关键点,
作出关键点关于对称轴的对应点,
依次连接这些对应点就能得到轴对称图形.
链接6
[重庆中考]如图5-Z-26,
在边长为1的小正方形组成的10×10网格中(我们把组成网格的小正方形的顶
点称为格点),
四边形ABCD在直线l的左侧,
其四个顶点A,
B,
C,
D都在网格的格点上.
请你在所给的网格中画出四边形A′B′C′D′,
使四边形A′B′C′D′和四边形ABCD关于直
线l对称,
其中点A′,
B′,C′,
D′分别是点A,
B,
C,
D的对应点.
图5-Z-26
解:
依次作出点A,
B,
C,
D关于
直线l的对应点A′,
B′,
C′,
D′,
顺
次连接即可.
如图5-Z-26.
图5-Z-26
谢
谢
观
看!
第五章 生活中的轴对称
章末复习
第五章 生活中的轴对称
章末复习
知识框架
归纳整合
素养提升
中考链接
知识框架
轴对称的性质
生活中的轴对称
简单的轴对称
图形
角
等腰三角形
轴对称现象
应用
线段
轴对称现象
轴对称图形
两个图形成轴对称
轴对称的性质
对应点所连的线段
被对称轴垂直平分
对应线段相等、
对应角相等
作对称点、对称线段
作轴对称图形
应用
设计轴对称图案
轴对称性
“三线合一”
等腰三角形
两底角相等
等边三角形
三边相等,
三个
内角均为60°
有三条对称轴
线段
轴对称性
线段垂直平分线的性质
角
轴对称性
角平分线的性质
【要点指导】轴对称图形的识别:方法1,
动手折叠,
再看折痕所在
直线两旁的两部分能不能“完全重合”;方法2,
找对应点,
也可以从反面入手,
即先找“对称轴”,
再看是不是每一个点都有关于这条直线对称的对应点,
如果有一个点没有对应点,
那么这个图形就不是轴对称图形.
归纳整合
专题一
轴对称图形的识别
例1
在下面由冬季奥运会比赛项目图标组成的四个图形中,
可以看作是轴对称图形的是(
).
图5-Z-1
D
相关题1
在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是(
).
A
图5-Z-2
【要点指导】与轴对称有关的作图题能有效地考查同学们的动手操作能力和空间想象能力,
一直是考试的热点.
考查的基本题型有:(1)画轴对称图形;(2)确定对应点;(3)确定对称轴.
作图的关键是作对称轴的垂线段,
确定原图形上的点关于对称轴的对应点.
专题二
与轴对称有关的作图问题及其应用
例2
如图5-Z-3所示,
已知△ABC和直线MN.
求作:△A′B′C′,
使
△A′B′C′和△ABC关于直线MN对称.(不要求写作法,
只保留作图痕迹)
图5-Z-3
分析
分别过点A,
B,
C作MN的垂线段并延长到点A′,
B′,
C′,
使点A′,B′,
C′到MN的垂线段的长度分别等于点A,
B,
C到MN的垂线段的长度,
连接A′B′,
A′C′,
B′C′,
即得△A′B′C′.
解:
如图5-Z-3所示.
图5-Z-3
相关题2
[绥化中考]如图5-Z-4,
在8×8的正方形网格中,
每个小正方形的边长都是1.已知△ABC的三个顶点都在格点上,
画出△ABC关于直线l对称的△A1
B1
C1
.
图5-Z-4
解:如图所示.
【要点指导】关于线段垂直平分线,
关键是要把握它的性质及与它有关的基本作图的步骤、技巧.借助“线段垂直平分线上的点到这条线段两端点的距离相等”,
实现相关线段的转移.
专题三
线段垂直平分线的性质及应用
例3
[遂宁中考]如图5-Z-5,
在△ABC中,
AC=4
cm,
线段AB的垂直平分线交AC于点N.
若△BCN的周长是7
cm,
则BC的长为(
).
A.1
cm
B.2
cm
C.3
cm
D.4
cm
图5-Z-5,
C
分析
因为MN是线段AB的垂直平分线,
所以AN=BN.
又因为△BCN的周长是7
cm,
所以AN+NC+BC=BN+NC+BC=7
cm,
而AN+NC=AC,
故AC+BC=7
cm.
因为AC=4
cm,
所以BC=7-4=3(cm).
相关题3
如图5-Z-6,
在△ABC中,分别以点A和点B为圆心,大于
AB的长为半径画弧,两弧相交于点M,
N,
作直线MN,
交BC于点D,
连接AD.
若△ADC的周长为10,AB=7,
则△ABC的周长为
(
).
A.7
B.14
C.17
D.20
图5-Z-6
C
[解析]由作图可知MN是线段AB的垂直平分线,得AD=BD,
所以△ABC的周长为AC+BC+AB=AC+CD+AD+AB=10+7=17.
故选C.
【要点指导】角是轴对称图形,
对称轴是角平分线所在的直线;角
平分线分得的两个角相等,
角平分线上的点到这个角的两边的距离相等,角平分线可以看作是到角两边距离相等的所有点的集合.
专题四
角平分线性质的运用
例4
如图5-Z-7,
在直角三角形ABC中,∠A=90°,
∠ABC的平分线BD交AC于点D,
AD=3,BC=10,
则△BDC的面积是 .
图5-Z-7
15
分析
过点D作DE⊥BC于点E,
则DE=AD=3.
又因为BC=10,
所以S
△BDC
=
BC·DE=
×10×3=15.
相关题4
如
图5
-Z
-8
,
OP
平分∠MON,
PA⊥ON于点A,
Q是射线OM上的一个动点.若PA=3,
则PQ的长不可能为(
).
A.1
B.3
C.5
D.7
图5
-Z
-8
A
[解析]如图,过点P作PQ⊥OM,垂足为Q,则此时PQ的长最小.
因为OP平分∠MON,PA⊥ON,PQ⊥OM,
所以PQ=PA=3,即PQ的最小值是3,不可能取1.
故选A.
【要点指导】折叠后的图形与折叠前的图形关于折痕所在的直线成轴对称,
即折叠前后的图形全等,
常利用这一点求线段的长或角的度数.
专题五
折叠中的对称
例5
如图5-Z-9所示,
把直角三角形纸片沿过顶点B的直线(BE交CA于点E)折叠,
直角顶点C落在斜边AB上,
如果折叠后得等腰三角形EBA,
那么下列结论:①∠ABC=60°;②点C与AB的中点重合;③点E到AB的距离等于CE的长.
其中正确的个数是(
).
A.0
B.1
C.2
D.3
图5-Z-9
D
分析
因为把直角三角形纸片沿过顶点B的直线(BE交CA于点E)折叠,
直角顶点C落在斜边AB上,
折叠后得等腰三角形EBA,
所以∠A=∠EBA,
∠CBE=∠EBA,所以∠A=∠CBE=∠EBA.
因为∠C=90°,所以∠A+∠CBE+∠EBA=90°,
所以∠A=∠CBE=∠EBA=30°,
所以∠ABC=60°,
故①正确.
因为∠A=∠EBA,
∠EDB=90°,所以AD=BD,
故②正确.
因为∠C=∠EDB=90°,
∠CBE=∠EBD=30°,
所以CE=DE(角平分线上的点到角两边的距离相等),
所以点E到AB的距离等于CE的长,
故③正确.
综上,
正确的有3个.
相关题5
[乌鲁木齐中考]如图5-Z-10,
△ABC的面积等于6,
边AC的长为3,
现将△ABC沿AB所在直线翻折,
使点C落在直线AD上的点C'处,
点P在直线AD上,
则线段BP的长不可能是(
).
A.3
B.4
C.5
D.6
A
图4-Z-10
【要点指导】等腰(等边)三角形是轴对称图形,
其对称轴是顶角平分线(或底边上的高或底边上的中线)所在的直线.
等腰三角形有以下性质:等腰三角形的两个底角相等(简写成“等边对等角”);等腰三角形的顶角平分线、底边上的中线、底边上的高重合(简称“三线合一”);等腰三角形的两底角的平分线相等;等腰三角形底边的垂直平分线上的点到两条腰的距离相等.
等边三角形是特殊的等腰三角形,
以上性质对等边三角形都适用.
专题六
等腰(等边)三角形性质的应用
例6
如图5-Z-11,
在直角三角形ABC中,∠C=90°,
直线BD交AC于点D,
把直角三角形沿着直线BD翻折,
点C恰好落在斜边AB上.
如果△ABD是等腰三角形,
那么∠A等于(
).
A.60°
B.45°
C.30°
D.22.5°
图5-Z-11
C
分析
根据题意,
得∠CBD=∠ABD.
因为△ABD是等腰三角形,
所以∠ABD=∠A,
所以∠ABD=∠A=∠CBD.
又因为∠C=90°,
所以∠A+∠ABC=3∠A=90°,
解得∠A=30°.
相关题6
[
黔
西
南
州
中
考
]
如
图5-Z-12,
已知△ABC是等边三角形,
点B,
C,
D,E在同一条直线上,
且CG=CD,
DF=DE,
则∠E=
°
.
15
图5-Z-12
【要点指导】线段的垂直平分线和角平分线性质的应用体现了数学建模思想,
解决这类题目的关键是:首先要理解题意,
把生活中的情景问题转化为数学模型来考虑;其次是用学过的知识来分析建立数学模型,
把复杂的问题分解成一个个我们熟悉的数学知识点来解决,
“分析——构建模型——设计方案——论证方案——得出结论”是解决此类题目的五个步骤.
素养提升
专题一
数学建模思想
例1
如图5-Z-13,
公路l同侧有A,
B两个工厂,
现要在公路上建一仓库.
(1)若要使仓库到A,
B两工厂的距离相等,
仓库应建在何处?
(2)若要使仓库到A,
B两工厂的距离之和最短,
仓库应建在何处?
图5-Z-13
分析
(1)由线段垂直平分线的性质可知仓库应建在线段AB的垂直平分线上.
又因为仓库在公路上,
所以线段AB的垂直平分线与公路l的交点即为仓库应建的地点.
(2)如果A,
B两点在直线l的两侧,
那么连接AB与l的交点即为所求,
由于现在A,
B两点在l的同侧,
因此可考虑作点A(或点B)关于l的对称点C,由轴对称的性质可知,
直线l上任意一点到点A,
C的距离相等,
这样就把直线l上一点到点A的距离转化为到点C的距离,
因此连接BC与l的交点即为所求.
解:
(1)如图5-Z-14①,
连接AB,
作AB的垂直平分线交直线l于点P,
点P就是所要求作的仓库的位置.
(2)如图5-Z-14②,
作点A关于直线l的对称点C,
连接BC交直线l于点D,点D就是所要求作的仓库的位置.
图5-Z-14
相关题1-1
如图5-Z-15,
需要在高速公路旁边修建一个飞机场,
使飞机场到A,
B两个城市的距离之和最小,
请作出机场的位置.
图5-Z-15
[解析]
利用轴对称的性质可作点A关于公路的对称点A′,连接A′B,与公路的交点就是飞机场的位置.
解:点P就是飞机场的位置.
相关题1-2
已知直线l及其两侧两点A,B,
如图5-Z-16.
(1)在直线l上作一点P,
使PA=PB;
(2)在直线l上作一点Q,
使l平分∠AQB.
(以上两小题保留作图痕迹,
标出必要的字母,
不要求写作法)
图5-Z-16
解:(1)作线段AB的垂直平分线与直线l的交点即为所求,图略.
(2)作点A关于直线l的对称点A′,连接BA′并延长交l于点Q,点Q即为所求,图略.
【要点指导】等腰三角形是一种特殊而又十分重要的三角形,它的边、角的特殊性在处理许多几何问题中起着关键的作用.
求解与等腰三角形的边、角有关的计算题时,
在条件不明确的情况下,
应根据题目的特点分类讨论.
专题二
分类讨论思想
例2
已知一个等腰三角形两个内角的度数之比为1∶4,
则这个等腰三角形顶角的度数为(
).
A.20°
B.120°
C.20°或120°
D.36°
C
分析
应分等腰三角形顶角与底角的度数之比为1∶4和等腰三角形底角与顶角的度数之比为1∶4两种情况讨论.
具体过程如下:设等腰三角形的顶角为α.
(1)若等腰三角形顶角与底角的度数之比为1∶4,
则α+4α+4α=180°,
解得α=20°;
(2)若等腰三角形底角与顶角的度数之比为1∶4,
则α+
α+
α=180°,
解得α=120°.
综上,
这个等腰三角形顶角的度数为20°或120°.
故选C.
相关题2
已知等腰三角形一腰上的中线把该三角形的周长分成18
cm和21
cm的两部分,
求该等腰三角形的各边长.
[解析]
画草图如图,腰AC上的中线BD把△ABC的周长分成18
cm和21
cm的两部分,列方程可解决问题.
中考链接
母题1
(教材P117习题5.1第1题)
观察下面的图形,
哪些图形是轴对称图形?如果是轴对称图形,
请画出对称轴.
图5-Z-17
考点:轴对称图形.
考情:主要考查轴对称图形及对称轴数量的判断,
多在选择题中出现.
策略:判断一个图形是不是轴对称图形,
可采用折叠的方法,
看折痕所在直线两边的部分是否能够重合.
若能找到一条直线,
使该图形沿着这条直线折叠,
直线两旁的部分互相重合,
则这个图形就是轴对称图形,
这条直线就是对称轴.
链接1
[天津中考]在一些美术字中,
有的汉字是轴对称图形.
下面4个汉字中,
可以看作是轴对称图形的是(
).
A
图5-Z-18
链接2
[广州中考]如图5-Z-19所示的五角星是轴对称图形,
它的对称轴共有(
).
A.1条 B.3条
C.5条 D.无数条
C
图5-Z-19
母题2
(教材P122随堂练习第3题)
如图5-Z-20,
在下面的等腰三角形中,
∠A是顶角,
分别求出它们的底角的度数.
图5-Z-20
考点:等腰三角形.
考情:主要考查等腰三角形的周长、边长及角度的计算.
策略:(1)等腰三角形中求角度时,
一定要分清顶角和底角.
若已知等腰三角形的顶角为x°,
则底角为
;若底角为x°,
则顶角为(180-2x)°.
(2)计算角的度数时,
往往结合三角形的内角和为180°,
运用方程思想计算.
链接3
[呼伦贝尔中考]如图5-Z-21,
在△ABC中,
AB=AC,过点A作AD∥BC.
若∠1=70°,则∠BAC的度数为(
).
A.40°
B.30°
C.70°
D.50°
A
图5-Z-21
分析
因为AD∥BC,
所以∠C=∠1=70°.
因为AB=AC,
所以∠B=∠C=70°,
所以∠BAC=180°-∠B-∠C=40°.
故选A.
链接4
[湖州中考]如图5-Z-22所示,
AD,
CE分别是△ABC的中线和角平分线.
若AB=AC,
∠CAD=20°,则∠ACE的度数是(
).
A.20°
B.35°
C.40°
D.70°
B
图5-Z-22
分析
因为AD是△ABC的中线,
AB=AC,∠CAD=20°,
所以∠CAB=2∠CAD=40°,
∠B=∠ACB=
(180°-∠CAB)=70°.
因为CE是△ABC的角平分线,
所以∠ACE=
∠ACB=35°.
母题3
(教材P124习题5.4第1题)
画一条线段AB,
利用尺规求作它的四等分点.
考点:线段垂直平分线、尺规作图.
考情:利用尺规作线段的垂直平分线.
策略:找线段的中点实际就是作线段的垂直平分线.
作四等分点,
就是连续作线段的垂直平分线.
线段的垂直平分线既垂直于线段又平分线段,作图要严格按照尺规作图的步骤,
保留作图痕迹.
链接5
[陕西中考]如图5-Z-23,
已知△ABC,请用尺规过点A作一条直线,
使其将△ABC分成面积相等的两部分.(保留作图痕迹,
不写作法)
图5-Z-23
解:
(1)分别以点B和C为圆心,
以大于
BC的长为半径画弧;
(2)连接两弧交点,
所得直线与BC交于点D,
作直线AD,
则直线AD就是所求作的直线,
如图5-Z-24.
图5-Z-24
母题4
(教材P133复习题第11题)
以虚线为对称轴画出图的另一半:
图5-Z-25
考点:
轴对称的性质.
考情:
主要考查轴对称作图.
策略:
作轴对称图形的关键是找准图形中的关键点,
作出关键点关于对称轴的对应点,
依次连接这些对应点就能得到轴对称图形.
链接6
[重庆中考]如图5-Z-26,
在边长为1的小正方形组成的10×10网格中(我们把组成网格的小正方形的顶
点称为格点),
四边形ABCD在直线l的左侧,
其四个顶点A,
B,
C,
D都在网格的格点上.
请你在所给的网格中画出四边形A′B′C′D′,
使四边形A′B′C′D′和四边形ABCD关于直
线l对称,
其中点A′,
B′,C′,
D′分别是点A,
B,
C,
D的对应点.
图5-Z-26
解:
依次作出点A,
B,
C,
D关于
直线l的对应点A′,
B′,
C′,
D′,
顺
次连接即可.
如图5-Z-26.
图5-Z-26
谢
谢
观
看!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
