2020-2021学年七年级数学北师大版下册单元检测试卷 第二章 相交线与平行线(A卷 )(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册单元检测试卷 第二章 相交线与平行线(A卷 )(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 139.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 18:02:08 | ||
图片预览

文档简介
自我综合评价(二)
[范围:第二章 相交线与平行线 时间:40分钟 分值:100分]
一、选择题(每小题4分,共32分)
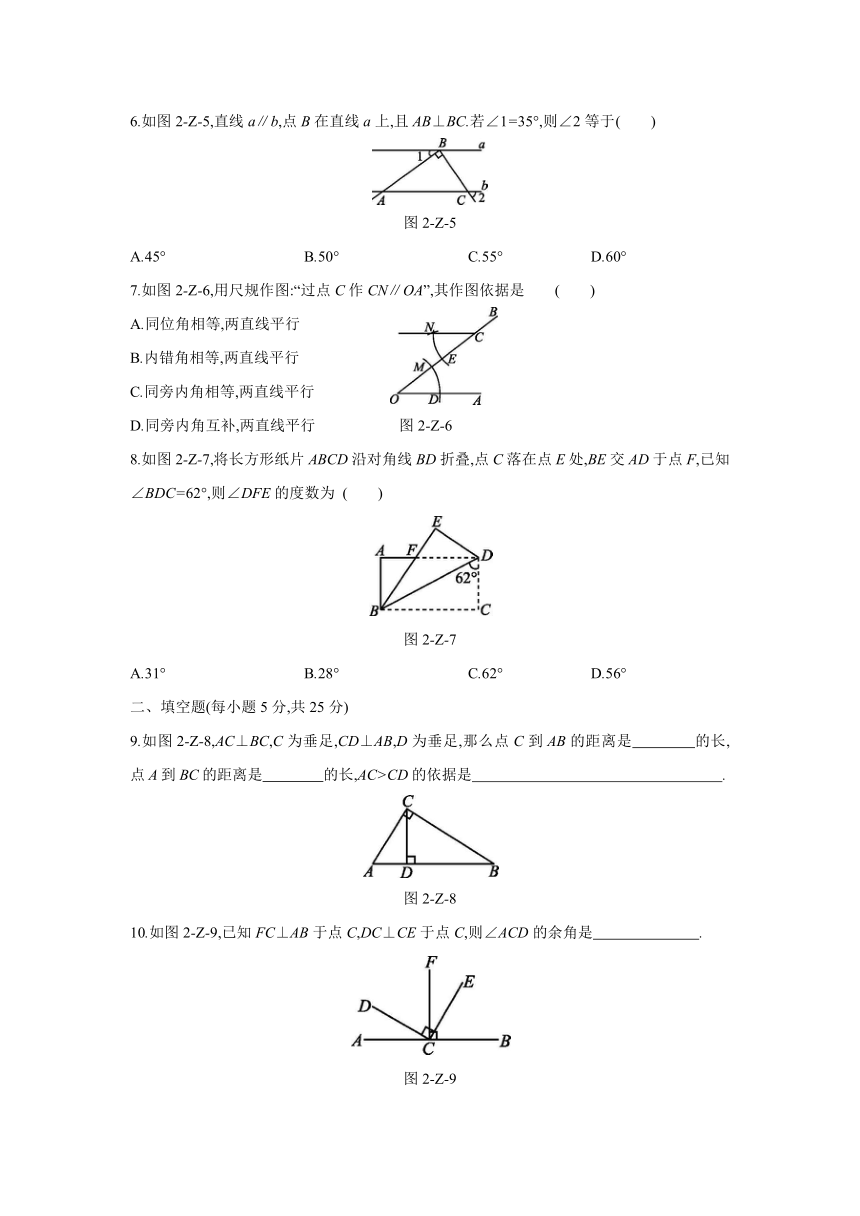
1.如图2-Z-1,直线AB,CD相交于点O,若∠AOC=30°,则∠BOD的度数为
( )
图2-Z-1
A.15°
B.30°
C.60°
D.150°
2.一个角的度数为42°,则它的余角的度数为
( )
A.48°
B.58°
C.138°
D.42°
3.如图2-Z-2,直线AB和CD相交于点O,OE⊥AB于点O,∠COE=55°,则∠AOD的度数为( )
图2-Z-2
A.145°
B.135°
C.125°
D.155°
4.如图2-Z-3所示,下列说法错误的是
( )
图2-Z-3
A.∠C与∠1是内错角B.∠2与∠3是内错角
C.∠A与∠B是同旁内角D.∠A与∠3是同位角
5.如图2-Z-4所示,下列由已知条件推出的结论错误的是
( )
图2-Z-4
A.由∠1=∠5,可以推出AB∥CD
B.由AD∥BC,可以推出∠4=∠8
C.由∠2=∠6,可以推出AD∥BC
D.由AD∥BC,可以推出∠3=∠7
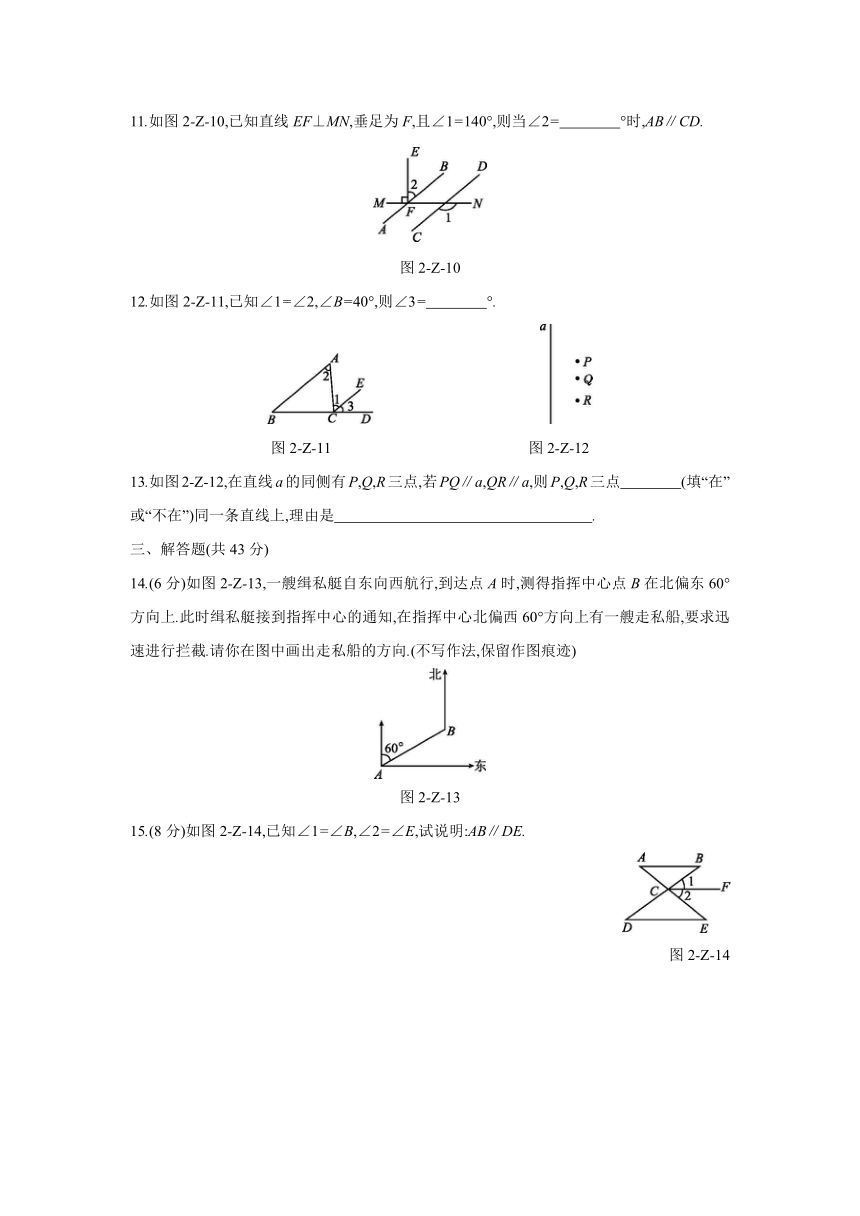
6.如图2-Z-5,直线a∥b,点B在直线a上,且AB⊥BC.若∠1=35°,则∠2等于
( )
图2-Z-5
A.45°
B.50°
C.55°
D.60°
7.如图2-Z-6,用尺规作图:“过点C作CN∥OA”,其作图依据是
( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角相等,两直线平行
D.同旁内角互补,两直线平行
图2-Z-6
8.如图2-Z-7,将长方形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为
( )
图2-Z-7
A.31°
B.28°
C.62°
D.56°
二、填空题(每小题5分,共25分)
9.如图2-Z-8,AC⊥BC,C为垂足,CD⊥AB,D为垂足,那么点C到AB的距离是 的长,点A到BC的距离是 的长,AC>CD的依据是
.?
图2-Z-8
10.如图2-Z-9,已知FC⊥AB于点C,DC⊥CE于点C,则∠ACD的余角是 .?
图2-Z-9
11.如图2-Z-10,已知直线EF⊥MN,垂足为F,且∠1=140°,则当∠2= °时,AB∥CD.?
图2-Z-10
12.如图2-Z-11,已知∠1=∠2,∠B=40°,则∠3= °.?
图2-Z-11
图2-Z-12
13.如图2-Z-12,在直线a的同侧有P,Q,R三点,若PQ∥a,QR∥a,则P,Q,R三点 (填“在”或“不在”)同一条直线上,理由是 .?
三、解答题(共43分)
14.(6分)如图2-Z-13,一艘缉私艇自东向西航行,到达点A时,测得指挥中心点B在北偏东60°方向上.此时缉私艇接到指挥中心的通知,在指挥中心北偏西60°方向上有一艘走私船,要求迅速进行拦截.请你在图中画出走私船的方向.(不写作法,保留作图痕迹)
图2-Z-13
15.(8分)如图2-Z-14,已知∠1=∠B,∠2=∠E,试说明:AB∥DE.
图2-Z-14
16.(8分)如图2-Z-15,EF∥AD,∠1=∠2,∠BAG=60°,求∠G的度数.
图2-Z-15
17.(10分)如图2-Z-16,已知∠1=70°,∠2=50°,∠D=70°,AE∥BC交CD于点E,求∠C的度数.
图2-Z-16
18.(11分)如图2-Z-17,已知AM∥BN,∠A=60°,P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD= .?
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC= .?
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律.
图2-Z-17
教师详解详析
1.B 2.A 3.A 4.B
5.B [解析]
B选项,由AB∥CD,可以推出∠4=∠8,故本选项错误.
6.C 7.B
8.D [解析]
先利用互余计算出∠FDB=∠CBD=28°,再根据折叠的性质得∠FBD=
∠CBD=28°,所以∠DFE=∠EBC=∠FBD+∠CBD=28°+28°=56°.
9.线段CD 线段AC 直线外一点与直线上各点连接的所有线段中,垂线段最短
10.∠DCF和∠ECB [解析]
因为FC⊥AB于点C,DC⊥CE于点C,
所以∠ACF=∠BCF=∠DCE=90°,
所以∠ACD+∠DCF=∠DCF+∠FCE=∠FCE+∠ECB=90°,
所以∠ACD=∠FCE,
所以∠ACD的余角是∠DCF和∠ECB.
11.50 [解析]
如图,利用直线AB∥CD,推知同位角∠3=∠4;然后根据平角的定义、垂直的性质以及等量代换,可求得∠2=50°.
12.40 [解析]
因为∠1=∠2,所以AB∥CE,所以∠3=∠B.因为∠B=40°,所以∠3=40°.
13.在 过直线外一点有且只有一条直线与这条直线平行
[解析]
因为PQ∥a,QR∥a,
所以P,Q,R三点在同一条直线上(过直线外一点有且只有一条直线与这条直线平行).
14.[解析]
要画出走私船的方向,只要过点B作出在正北方向线的左边且夹角是60°的一条射线即可.具体作法是以点B为顶点,BD为一边,在射线BD的左边作∠DBE=∠BAC.
解:如图,射线BE为走私船的方向.
15.解:因为∠1=∠B(已知),
所以AB∥CF(内错角相等,两直线平行).
因为∠2=∠E(已知),
所以CF∥DE(内错角相等,两直线平行),
所以AB∥DE(平行于同一条直线的两条直线平行).
16.解:因为EF∥AD,
所以∠2=∠BAD.
因为∠1=∠2,
所以∠1=∠BAD,
所以DG∥AB,
所以∠G+∠BAG=180°.
因为∠BAG=60°,
所以∠G=180°-∠BAG=180°-60°=120°.
17.解:因为∠1=70°,∠D=70°,
所以∠1=∠D,所以AB∥CD,
所以∠2=∠AED.
因为∠2=50°,所以∠AED=50°.
因为AE∥BC,
所以∠C=∠AED=50°.
18.解:(1)因为AM∥BN,
所以∠ABN=180°-∠A=120°.
又因为BC,BD分别平分∠ABP和∠PBN,
所以∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,故答案为60°.
(2)因为AM∥BN,所以∠ACB=∠CBN.
又因为∠ACB=∠ABD,所以∠CBN=∠ABD,
所以∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,
所以∠ABC=∠CBP=∠DBP=∠DBN,
所以∠ABC=∠ABN=30°.故答案为30°.
(3)不变.因为AM∥BN,所以∠APB=∠PBN,∠ADB=∠DBN.
又因为BD平分∠PBN,
所以∠ADB=∠DBN=∠PBN=∠APB,故∠APB∶∠ADB=2∶1.
[范围:第二章 相交线与平行线 时间:40分钟 分值:100分]
一、选择题(每小题4分,共32分)
1.如图2-Z-1,直线AB,CD相交于点O,若∠AOC=30°,则∠BOD的度数为
( )
图2-Z-1
A.15°
B.30°
C.60°
D.150°
2.一个角的度数为42°,则它的余角的度数为
( )
A.48°
B.58°
C.138°
D.42°
3.如图2-Z-2,直线AB和CD相交于点O,OE⊥AB于点O,∠COE=55°,则∠AOD的度数为( )
图2-Z-2
A.145°
B.135°
C.125°
D.155°
4.如图2-Z-3所示,下列说法错误的是
( )
图2-Z-3
A.∠C与∠1是内错角B.∠2与∠3是内错角
C.∠A与∠B是同旁内角D.∠A与∠3是同位角
5.如图2-Z-4所示,下列由已知条件推出的结论错误的是
( )
图2-Z-4
A.由∠1=∠5,可以推出AB∥CD
B.由AD∥BC,可以推出∠4=∠8
C.由∠2=∠6,可以推出AD∥BC
D.由AD∥BC,可以推出∠3=∠7
6.如图2-Z-5,直线a∥b,点B在直线a上,且AB⊥BC.若∠1=35°,则∠2等于
( )
图2-Z-5
A.45°
B.50°
C.55°
D.60°
7.如图2-Z-6,用尺规作图:“过点C作CN∥OA”,其作图依据是
( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角相等,两直线平行
D.同旁内角互补,两直线平行
图2-Z-6
8.如图2-Z-7,将长方形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为
( )
图2-Z-7
A.31°
B.28°
C.62°
D.56°
二、填空题(每小题5分,共25分)
9.如图2-Z-8,AC⊥BC,C为垂足,CD⊥AB,D为垂足,那么点C到AB的距离是 的长,点A到BC的距离是 的长,AC>CD的依据是
.?
图2-Z-8
10.如图2-Z-9,已知FC⊥AB于点C,DC⊥CE于点C,则∠ACD的余角是 .?
图2-Z-9
11.如图2-Z-10,已知直线EF⊥MN,垂足为F,且∠1=140°,则当∠2= °时,AB∥CD.?
图2-Z-10
12.如图2-Z-11,已知∠1=∠2,∠B=40°,则∠3= °.?
图2-Z-11
图2-Z-12
13.如图2-Z-12,在直线a的同侧有P,Q,R三点,若PQ∥a,QR∥a,则P,Q,R三点 (填“在”或“不在”)同一条直线上,理由是 .?
三、解答题(共43分)
14.(6分)如图2-Z-13,一艘缉私艇自东向西航行,到达点A时,测得指挥中心点B在北偏东60°方向上.此时缉私艇接到指挥中心的通知,在指挥中心北偏西60°方向上有一艘走私船,要求迅速进行拦截.请你在图中画出走私船的方向.(不写作法,保留作图痕迹)
图2-Z-13
15.(8分)如图2-Z-14,已知∠1=∠B,∠2=∠E,试说明:AB∥DE.
图2-Z-14
16.(8分)如图2-Z-15,EF∥AD,∠1=∠2,∠BAG=60°,求∠G的度数.
图2-Z-15
17.(10分)如图2-Z-16,已知∠1=70°,∠2=50°,∠D=70°,AE∥BC交CD于点E,求∠C的度数.
图2-Z-16
18.(11分)如图2-Z-17,已知AM∥BN,∠A=60°,P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD= .?
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC= .?
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律.
图2-Z-17
教师详解详析
1.B 2.A 3.A 4.B
5.B [解析]
B选项,由AB∥CD,可以推出∠4=∠8,故本选项错误.
6.C 7.B
8.D [解析]
先利用互余计算出∠FDB=∠CBD=28°,再根据折叠的性质得∠FBD=
∠CBD=28°,所以∠DFE=∠EBC=∠FBD+∠CBD=28°+28°=56°.
9.线段CD 线段AC 直线外一点与直线上各点连接的所有线段中,垂线段最短
10.∠DCF和∠ECB [解析]
因为FC⊥AB于点C,DC⊥CE于点C,
所以∠ACF=∠BCF=∠DCE=90°,
所以∠ACD+∠DCF=∠DCF+∠FCE=∠FCE+∠ECB=90°,
所以∠ACD=∠FCE,
所以∠ACD的余角是∠DCF和∠ECB.
11.50 [解析]
如图,利用直线AB∥CD,推知同位角∠3=∠4;然后根据平角的定义、垂直的性质以及等量代换,可求得∠2=50°.
12.40 [解析]
因为∠1=∠2,所以AB∥CE,所以∠3=∠B.因为∠B=40°,所以∠3=40°.
13.在 过直线外一点有且只有一条直线与这条直线平行
[解析]
因为PQ∥a,QR∥a,
所以P,Q,R三点在同一条直线上(过直线外一点有且只有一条直线与这条直线平行).
14.[解析]
要画出走私船的方向,只要过点B作出在正北方向线的左边且夹角是60°的一条射线即可.具体作法是以点B为顶点,BD为一边,在射线BD的左边作∠DBE=∠BAC.
解:如图,射线BE为走私船的方向.
15.解:因为∠1=∠B(已知),
所以AB∥CF(内错角相等,两直线平行).
因为∠2=∠E(已知),
所以CF∥DE(内错角相等,两直线平行),
所以AB∥DE(平行于同一条直线的两条直线平行).
16.解:因为EF∥AD,
所以∠2=∠BAD.
因为∠1=∠2,
所以∠1=∠BAD,
所以DG∥AB,
所以∠G+∠BAG=180°.
因为∠BAG=60°,
所以∠G=180°-∠BAG=180°-60°=120°.
17.解:因为∠1=70°,∠D=70°,
所以∠1=∠D,所以AB∥CD,
所以∠2=∠AED.
因为∠2=50°,所以∠AED=50°.
因为AE∥BC,
所以∠C=∠AED=50°.
18.解:(1)因为AM∥BN,
所以∠ABN=180°-∠A=120°.
又因为BC,BD分别平分∠ABP和∠PBN,
所以∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,故答案为60°.
(2)因为AM∥BN,所以∠ACB=∠CBN.
又因为∠ACB=∠ABD,所以∠CBN=∠ABD,
所以∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,
所以∠ABC=∠CBP=∠DBP=∠DBN,
所以∠ABC=∠ABN=30°.故答案为30°.
(3)不变.因为AM∥BN,所以∠APB=∠PBN,∠ADB=∠DBN.
又因为BD平分∠PBN,
所以∠ADB=∠DBN=∠PBN=∠APB,故∠APB∶∠ADB=2∶1.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
