2020-2021学年七年级数学北师大版下册单元检测试卷 第三章 变量之间的关系(B卷)(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册单元检测试卷 第三章 变量之间的关系(B卷)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 230.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 17:59:11 | ||
图片预览



文档简介
第三章综合提升卷
范围:变量之间的关系 时间:90分钟 分值:100分
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.地表以下岩层的温度随着所处深度的变化而变化,在这一问题中因变量是
( )
A.地表
B.岩层的温度
C.所处深度
D.时间
2.如图3-Z-1是某市某天的气温随时间变化的图象,通过观察可知,下列说法中错误的是( )
图3-Z-1
A.这天15点时气温最高
B.这天3点时气温最低
C.这天最高气温与最低气温的差是13
℃
D.这天21点时气温是30
℃
3.长方形的周长为24
cm,一边长为x
cm(其中x>0),面积为y
cm2,则这样的长方形中y与x之间的关系式可以写为
( )
A.y=x2
B.y=(12-x)2
C.y=(12-x)·x
D.y=2(12-x)
4.变量y与x之间的关系式是y=x2+1,当自变量x=2时,因变量y的值是
( )
A.-2
B.-1
C.1
D.3
5.在边长为20
cm的正方形中,挖去一个边长为x
cm的小正方形.当小正方形的边长x从小到大变化时,剩余部分的面积y(cm2)随之发生变化,那么y随x变化的关系式为
( )
A.y=400-x2
B.y=40-2x
C.y=400-2x
D.y=40-2x2
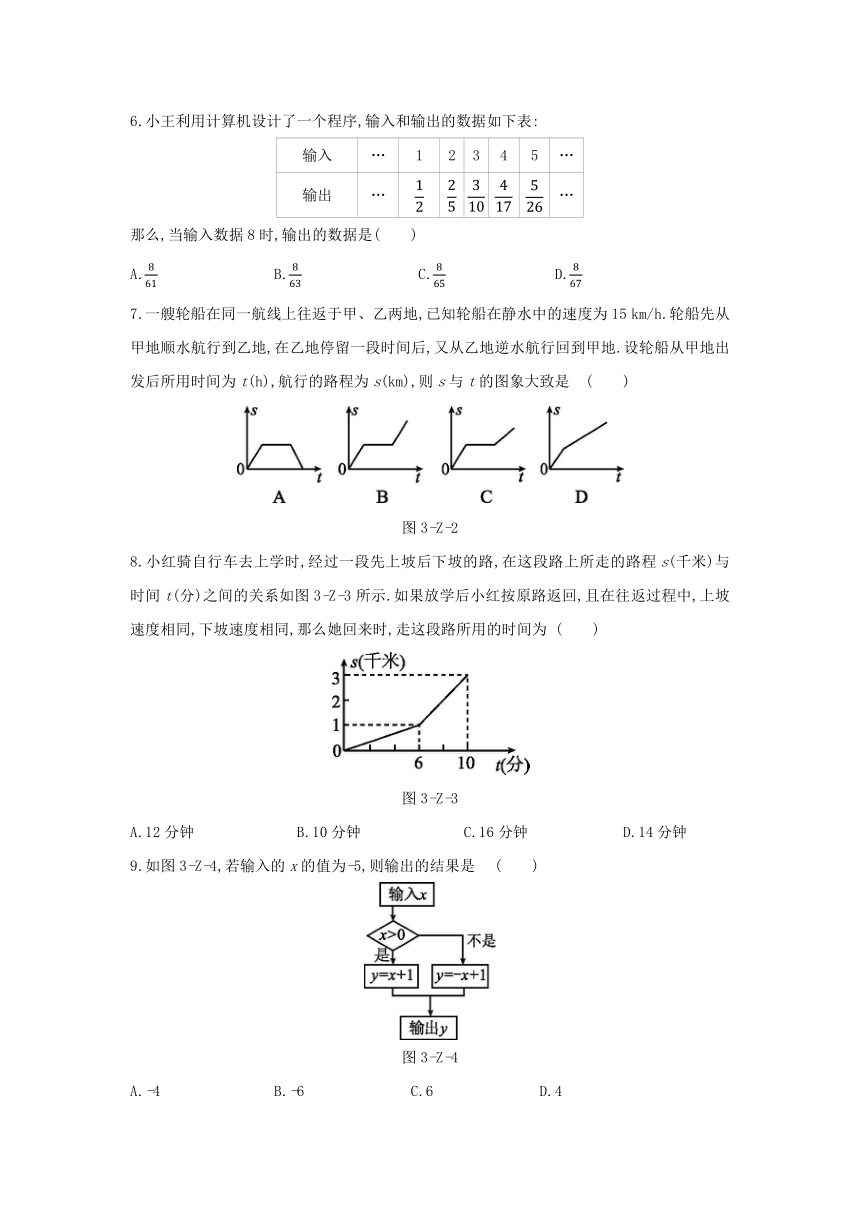
6.小王利用计算机设计了一个程序,输入和输出的数据如下表:
输入
…
1
2
3
4
5
…
输出
…
…
那么,当输入数据8时,输出的数据是( )
A.
B.
C.
D.
7.一艘轮船在同一航线上往返于甲、乙两地,已知轮船在静水中的速度为15
km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的图象大致是
( )
图3-Z-2
8.小红骑自行车去上学时,经过一段先上坡后下坡的路,在这段路上所走的路程s(千米)与时间t(分)之间的关系如图3-Z-3所示.如果放学后小红按原路返回,且在往返过程中,上坡速度相同,下坡速度相同,那么她回来时,走这段路所用的时间为
( )
图3-Z-3
A.12分钟
B.10分钟
C.16分钟
D.14分钟
9.如图3-Z-4,若输入的x的值为-5,则输出的结果是
( )
图3-Z-4
A.-4
B.-6
C.6
D.4
10.图3-Z-5表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶的路程随时间变化的图象,根据图象信息,下列结论中错误的是
( )
图3-Z-5
A.轮船的速度为20千米/时
B.快艇的速度为40千米/时
C.轮船比快艇先出发2小时
D.快艇不能赶上轮船
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷 (非选择题 共70分)
二、填空题(每小题4分,共20分)
11.圆柱的高是6
cm,当圆柱的底面半径r(cm)由小到大变化时,圆柱的体积V(cm3)也随之发生变化.在这个变化过程中,自变量是 ,因变量是 .?
12.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,那么超过2千克的部分其价格打6折.设购买种子的数量为x(x>2)千克,付款金额为y元,则y与x之间的关系式为 .?
13.某公交车每月的利润y(元)与乘客人数x(人)之间的关系式为y=2.5x-6000,该公交车为使每月不亏损,则每月乘客量至少需达到 人.?
14.A,B两地相距20千米,甲、乙两人都从A地去B地,图3-Z-6中的l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(时)之间的关系.有下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/时;④乙先到达B地.其中正确的是 .(填序号)?
图3-Z-6
15.如图3-Z-7是用棋子摆成的“上”字形图案:
图3-Z-7
按照以上的规律继续摆下去,通过观察,可以发现:
(1)第五个“上”字需用 枚棋子;?
(2)第n个“上”字需用 枚棋子.?
三、解答题(共50分)
16.(4分)下表是佳佳往同学家打长途电话的几次收费记录:
通话时间/分
1
2
3
4
5
6
7
电话费/元
0.6
1.2
1.8
2.4
3.0
3.6
4.2
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)请你帮佳佳预测一下,若她打电话所用的时间是10分钟,则需付多少元电话费?
17.(6分)某商店出售一种商品,质量x(千克)与售价y(元)之间的关系如下表:
质量x(千克)
售价y(元)
1
6+0.05
2
12+0.05
3
18+0.05
4
24+0.05
…
…
(1)写出售价y(元)与质量x(千克)之间的关系式: ;?
(2)小张想买此种商品7.5千克,应付款多少元?
(3)若小张花费了60.05元购买此种商品,则小张购买了多少千克此种商品?
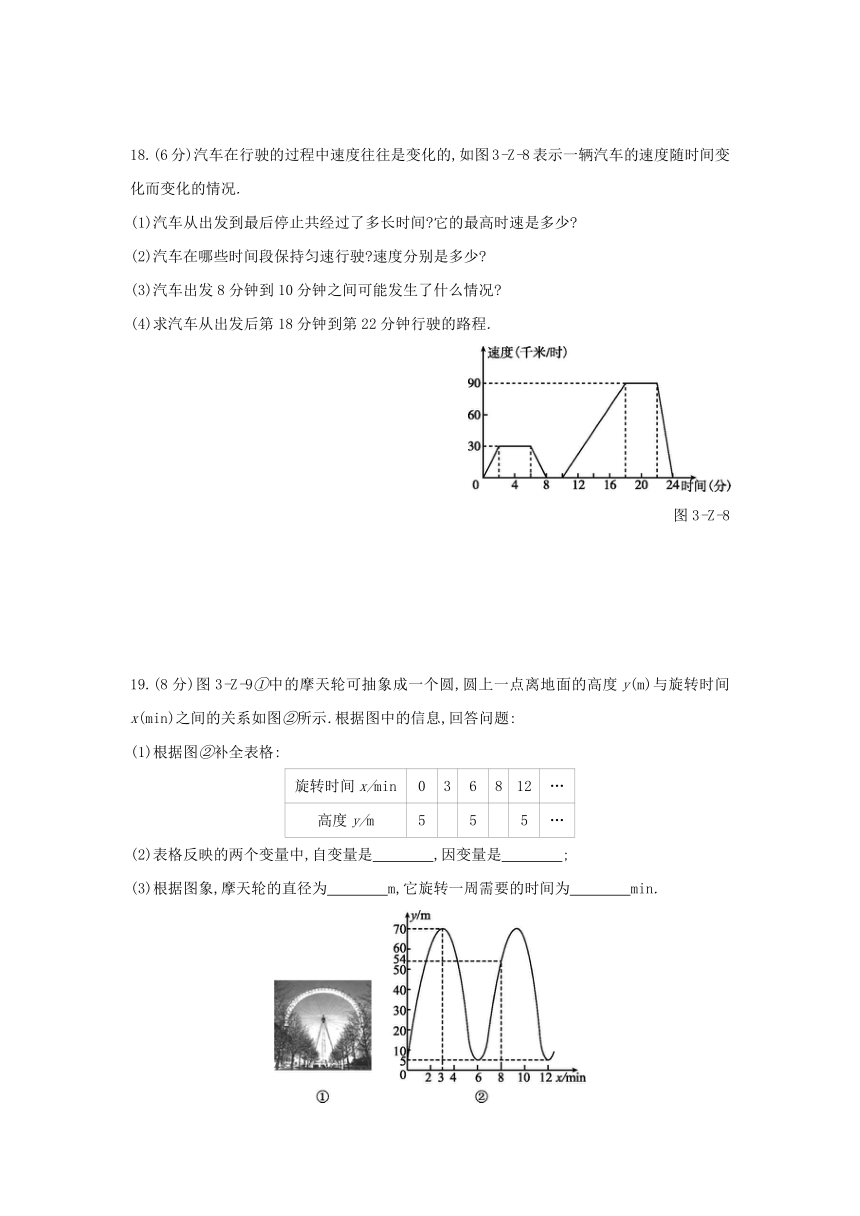
18.(6分)汽车在行驶的过程中速度往往是变化的,如图3-Z-8表示一辆汽车的速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多长时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?速度分别是多少?
(3)汽车出发8分钟到10分钟之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
图3-Z-8
19.(8分)图3-Z-9①中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图②所示.根据图中的信息,回答问题:
(1)根据图②补全表格:
旋转时间x/min
0
3
6
8
12
…
高度y/m
5
5
5
…
(2)表格反映的两个变量中,自变量是 ,因变量是 ;?
(3)根据图象,摩天轮的直径为 m,它旋转一周需要的时间为 min.?
图3-Z-9
20.(8分)如图3-Z-10,已知三角形ABC的面积是12
cm2,BC=6
cm,在BC边上有一动点P(点P与点B不重合),连接AP,设BP=x
cm,S三角形ABP=y
cm2.
(1)写出y与x之间的关系式;
(2)用表格表示当x从1变到6时(每次增加1),y相应的值;
(3)当x每增加1时,y如何变化?
(4)当x=2.5时,y等于什么?
图3-Z-10
21.(8分)心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)(其中2≤x≤20)之间有如下关系:
提出概念所用的时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)上表中反映了哪两个变量之间的关系?
(2)当提出概念所用的时间是10分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念所用的时间为多少时,学生的接受能力最强?
(4)从表中可知,当时间x在什么范围内时,学生的接受能力逐步增强?当时间x在什么范围内时,学生的接受能力逐步降低?
22.(10分)“龟兔赛跑”的故事同学们都非常熟悉,图3-Z-11中的线段OD和折线OABC表示“龟兔赛跑”时路程s(米)与时间t(分)的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中
的路程与时间的关系,比赛的全程是 米.?
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多长时间.
图3-Z-11
典题讲评与答案详析
第三章综合提升卷
1.B
2.C
3.C
4.D
5.A
6.C [解析]
分母是输入数的平方再加1,分子是输入的数.
7.C
8.D
9.C
10.D
11.r V
12.y=3x+4 [解析]
y=10+(x-2)×5×0.6=3x+4.
13.2400 [解析]
根据题意,得2.5x-6000=0,
解得x=2400.
即该公交车为使每月不亏损,每月乘客量至少需达到2400人.
故答案为2400.
14.①③④
15.22 (4n+2)
16.解:(1)表格反映了通话时间与电话费之间的关系,其中通话时间是自变量,电话费是因变量.
(2)设通话时间为x分钟时,电话费为y元,则有
y=0.6x,所以当x=10时,y=6.
故若她打电话所用的时间是10分钟,则需付6元电话费.
17.解:(1)根据表格分析可得:质量x(千克)每增加1,售价y(元)就增加6,
故售价y(元)与质量x(千克)之间的关系式是y=6x+0.05.
(2)将x=7.5代入(1)中关系式可得:y=6×7.5+0.05=45.05.
所以买此种商品7.5千克,应付款45.05元.
(3)当y=60.05时,即6x+0.05=60.05,
解得x=10.
所以小张购买了10千克此种商品.
18.解:(1)汽车从出发到最后停止共经过了24分钟,它的最高时速是90千米/时.
(2)汽车在2分钟到6分钟,18分钟到22分钟保持匀速行驶,速度分别是30千米/时和90千米/时.
(3)汽车出发8分钟到10分钟之间处于静止状态,可能是遇到红灯了.(合理即可)
(4)汽车从出发后第18分钟到第22分钟行驶的路程=90×=6(千米).
19.解:(1)由图象可知,当x=3时,y=70,
当x=8时,y=54.
故答案为70;54.
(2)表格反映的两个变量中,自变量是旋转时间x,因变量是高度y.
故答案为旋转时间x;高度y.
(3)由图象可知,摩天轮的直径为70-5=65(m),旋转一周需要的时间为6
min.
故答案为65;6.
20.解:作三角形ABC中BC边上的高AD,则AD也是三角形ABP中BP边上的高.
(1)因为S三角形ABC=BC·AD,
所以12=×6AD,所以AD=4(cm).
因为S三角形ABP=BP·AD,
所以y=·x·4,即y=2x(0(2)如下表所示:
x(cm)
1
2
3
4
5
6
y(cm2)
2
4
6
8
10
12
(3)当x每增加1时,y增加2,可从表格和关系式y=2x中得到这种规律.
(4)当x=2.5时,y=5.
21.解:(1)反映了提出概念所用的时间x和学生对概念的接受能力y之间的关系.
(2)当x=10时,y=59,
所以学生的接受能力是59.
(3)当x=13时,y的值最大,最大值是59.9,
所以提出概念所用的时间为13分钟时,学生的接受能力最强.
(4)由表中数据可知:当时间x在2分钟至13分钟范围内时,y值逐渐增大,即学生的接受能力逐步增强;当时间x在13分钟至20分钟范围内时,y值逐渐减小,即学生的接受能力逐步降低.
22.解:(1)兔子 乌龟 1500
(2)结合图象得出:
700÷1=700(米/分);
1500÷30=50(米/分).
故兔子起初每分钟跑700米,乌龟每分钟爬50米.
(3)700÷50=14(分).
答:乌龟用了14分钟追上了正在睡觉的兔子.
(4)因为48千米=48000米,
所以48000÷60=800(米/分),
(1500-700)÷800=1(分).
30+0.5-1×2=28.5(分).
故兔子中间停下睡觉用了28.5分钟.
范围:变量之间的关系 时间:90分钟 分值:100分
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.地表以下岩层的温度随着所处深度的变化而变化,在这一问题中因变量是
( )
A.地表
B.岩层的温度
C.所处深度
D.时间
2.如图3-Z-1是某市某天的气温随时间变化的图象,通过观察可知,下列说法中错误的是( )
图3-Z-1
A.这天15点时气温最高
B.这天3点时气温最低
C.这天最高气温与最低气温的差是13
℃
D.这天21点时气温是30
℃
3.长方形的周长为24
cm,一边长为x
cm(其中x>0),面积为y
cm2,则这样的长方形中y与x之间的关系式可以写为
( )
A.y=x2
B.y=(12-x)2
C.y=(12-x)·x
D.y=2(12-x)
4.变量y与x之间的关系式是y=x2+1,当自变量x=2时,因变量y的值是
( )
A.-2
B.-1
C.1
D.3
5.在边长为20
cm的正方形中,挖去一个边长为x
cm的小正方形.当小正方形的边长x从小到大变化时,剩余部分的面积y(cm2)随之发生变化,那么y随x变化的关系式为
( )
A.y=400-x2
B.y=40-2x
C.y=400-2x
D.y=40-2x2
6.小王利用计算机设计了一个程序,输入和输出的数据如下表:
输入
…
1
2
3
4
5
…
输出
…
…
那么,当输入数据8时,输出的数据是( )
A.
B.
C.
D.
7.一艘轮船在同一航线上往返于甲、乙两地,已知轮船在静水中的速度为15
km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的图象大致是
( )
图3-Z-2
8.小红骑自行车去上学时,经过一段先上坡后下坡的路,在这段路上所走的路程s(千米)与时间t(分)之间的关系如图3-Z-3所示.如果放学后小红按原路返回,且在往返过程中,上坡速度相同,下坡速度相同,那么她回来时,走这段路所用的时间为
( )
图3-Z-3
A.12分钟
B.10分钟
C.16分钟
D.14分钟
9.如图3-Z-4,若输入的x的值为-5,则输出的结果是
( )
图3-Z-4
A.-4
B.-6
C.6
D.4
10.图3-Z-5表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶的路程随时间变化的图象,根据图象信息,下列结论中错误的是
( )
图3-Z-5
A.轮船的速度为20千米/时
B.快艇的速度为40千米/时
C.轮船比快艇先出发2小时
D.快艇不能赶上轮船
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷 (非选择题 共70分)
二、填空题(每小题4分,共20分)
11.圆柱的高是6
cm,当圆柱的底面半径r(cm)由小到大变化时,圆柱的体积V(cm3)也随之发生变化.在这个变化过程中,自变量是 ,因变量是 .?
12.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,那么超过2千克的部分其价格打6折.设购买种子的数量为x(x>2)千克,付款金额为y元,则y与x之间的关系式为 .?
13.某公交车每月的利润y(元)与乘客人数x(人)之间的关系式为y=2.5x-6000,该公交车为使每月不亏损,则每月乘客量至少需达到 人.?
14.A,B两地相距20千米,甲、乙两人都从A地去B地,图3-Z-6中的l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(时)之间的关系.有下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/时;④乙先到达B地.其中正确的是 .(填序号)?
图3-Z-6
15.如图3-Z-7是用棋子摆成的“上”字形图案:
图3-Z-7
按照以上的规律继续摆下去,通过观察,可以发现:
(1)第五个“上”字需用 枚棋子;?
(2)第n个“上”字需用 枚棋子.?
三、解答题(共50分)
16.(4分)下表是佳佳往同学家打长途电话的几次收费记录:
通话时间/分
1
2
3
4
5
6
7
电话费/元
0.6
1.2
1.8
2.4
3.0
3.6
4.2
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)请你帮佳佳预测一下,若她打电话所用的时间是10分钟,则需付多少元电话费?
17.(6分)某商店出售一种商品,质量x(千克)与售价y(元)之间的关系如下表:
质量x(千克)
售价y(元)
1
6+0.05
2
12+0.05
3
18+0.05
4
24+0.05
…
…
(1)写出售价y(元)与质量x(千克)之间的关系式: ;?
(2)小张想买此种商品7.5千克,应付款多少元?
(3)若小张花费了60.05元购买此种商品,则小张购买了多少千克此种商品?
18.(6分)汽车在行驶的过程中速度往往是变化的,如图3-Z-8表示一辆汽车的速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多长时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?速度分别是多少?
(3)汽车出发8分钟到10分钟之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
图3-Z-8
19.(8分)图3-Z-9①中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图②所示.根据图中的信息,回答问题:
(1)根据图②补全表格:
旋转时间x/min
0
3
6
8
12
…
高度y/m
5
5
5
…
(2)表格反映的两个变量中,自变量是 ,因变量是 ;?
(3)根据图象,摩天轮的直径为 m,它旋转一周需要的时间为 min.?
图3-Z-9
20.(8分)如图3-Z-10,已知三角形ABC的面积是12
cm2,BC=6
cm,在BC边上有一动点P(点P与点B不重合),连接AP,设BP=x
cm,S三角形ABP=y
cm2.
(1)写出y与x之间的关系式;
(2)用表格表示当x从1变到6时(每次增加1),y相应的值;
(3)当x每增加1时,y如何变化?
(4)当x=2.5时,y等于什么?
图3-Z-10
21.(8分)心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)(其中2≤x≤20)之间有如下关系:
提出概念所用的时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)上表中反映了哪两个变量之间的关系?
(2)当提出概念所用的时间是10分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念所用的时间为多少时,学生的接受能力最强?
(4)从表中可知,当时间x在什么范围内时,学生的接受能力逐步增强?当时间x在什么范围内时,学生的接受能力逐步降低?
22.(10分)“龟兔赛跑”的故事同学们都非常熟悉,图3-Z-11中的线段OD和折线OABC表示“龟兔赛跑”时路程s(米)与时间t(分)的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中
的路程与时间的关系,比赛的全程是 米.?
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多长时间.
图3-Z-11
典题讲评与答案详析
第三章综合提升卷
1.B
2.C
3.C
4.D
5.A
6.C [解析]
分母是输入数的平方再加1,分子是输入的数.
7.C
8.D
9.C
10.D
11.r V
12.y=3x+4 [解析]
y=10+(x-2)×5×0.6=3x+4.
13.2400 [解析]
根据题意,得2.5x-6000=0,
解得x=2400.
即该公交车为使每月不亏损,每月乘客量至少需达到2400人.
故答案为2400.
14.①③④
15.22 (4n+2)
16.解:(1)表格反映了通话时间与电话费之间的关系,其中通话时间是自变量,电话费是因变量.
(2)设通话时间为x分钟时,电话费为y元,则有
y=0.6x,所以当x=10时,y=6.
故若她打电话所用的时间是10分钟,则需付6元电话费.
17.解:(1)根据表格分析可得:质量x(千克)每增加1,售价y(元)就增加6,
故售价y(元)与质量x(千克)之间的关系式是y=6x+0.05.
(2)将x=7.5代入(1)中关系式可得:y=6×7.5+0.05=45.05.
所以买此种商品7.5千克,应付款45.05元.
(3)当y=60.05时,即6x+0.05=60.05,
解得x=10.
所以小张购买了10千克此种商品.
18.解:(1)汽车从出发到最后停止共经过了24分钟,它的最高时速是90千米/时.
(2)汽车在2分钟到6分钟,18分钟到22分钟保持匀速行驶,速度分别是30千米/时和90千米/时.
(3)汽车出发8分钟到10分钟之间处于静止状态,可能是遇到红灯了.(合理即可)
(4)汽车从出发后第18分钟到第22分钟行驶的路程=90×=6(千米).
19.解:(1)由图象可知,当x=3时,y=70,
当x=8时,y=54.
故答案为70;54.
(2)表格反映的两个变量中,自变量是旋转时间x,因变量是高度y.
故答案为旋转时间x;高度y.
(3)由图象可知,摩天轮的直径为70-5=65(m),旋转一周需要的时间为6
min.
故答案为65;6.
20.解:作三角形ABC中BC边上的高AD,则AD也是三角形ABP中BP边上的高.
(1)因为S三角形ABC=BC·AD,
所以12=×6AD,所以AD=4(cm).
因为S三角形ABP=BP·AD,
所以y=·x·4,即y=2x(0
x(cm)
1
2
3
4
5
6
y(cm2)
2
4
6
8
10
12
(3)当x每增加1时,y增加2,可从表格和关系式y=2x中得到这种规律.
(4)当x=2.5时,y=5.
21.解:(1)反映了提出概念所用的时间x和学生对概念的接受能力y之间的关系.
(2)当x=10时,y=59,
所以学生的接受能力是59.
(3)当x=13时,y的值最大,最大值是59.9,
所以提出概念所用的时间为13分钟时,学生的接受能力最强.
(4)由表中数据可知:当时间x在2分钟至13分钟范围内时,y值逐渐增大,即学生的接受能力逐步增强;当时间x在13分钟至20分钟范围内时,y值逐渐减小,即学生的接受能力逐步降低.
22.解:(1)兔子 乌龟 1500
(2)结合图象得出:
700÷1=700(米/分);
1500÷30=50(米/分).
故兔子起初每分钟跑700米,乌龟每分钟爬50米.
(3)700÷50=14(分).
答:乌龟用了14分钟追上了正在睡觉的兔子.
(4)因为48千米=48000米,
所以48000÷60=800(米/分),
(1500-700)÷800=1(分).
30+0.5-1×2=28.5(分).
故兔子中间停下睡觉用了28.5分钟.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
