2020-2021学年七年级数学北师大版下册单元检测试卷 第五章 生活中的轴对称(A卷)(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册单元检测试卷 第五章 生活中的轴对称(A卷)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 17:53:52 | ||
图片预览

文档简介
自我综合评价(五)
[范围:第五章 生活中的轴对称 时间:40分钟 分值:100分]
一、选择题(每小题4分,共24分)
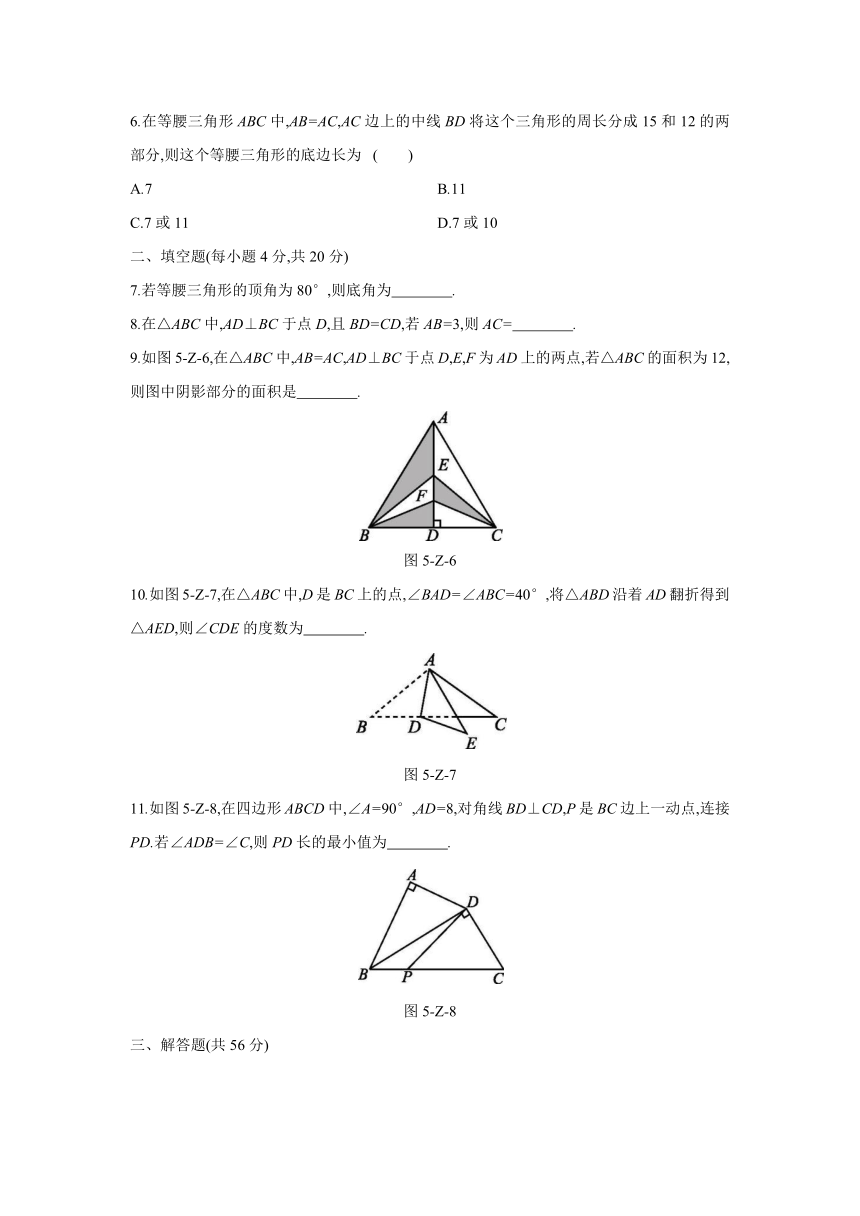
1.图5-Z-1中的轴对称图形是
( )
图5-Z-1
2.如图5-Z-2,将一张三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是
( )
A.AD=BC
B.AE=AC
C.ED+EB=DB
D.AE+CB=AB
图5-Z-2
3.观察图5-Z-3中尺规作图的痕迹,下列说法错误的是
( )
A.OE是∠AOB的平分线
B.OC=OD
C.点C,D到OE的距离不相等
D.∠AOE=∠BOE
图5-Z-3
4.如图5-Z-4,BD,CE分别是△ABC的高线和角平分线,且相交于点O.若AB=AC,∠A=40°,则∠BOE的度数是
( )
A.60°
B.55°
C.50°
D.40°
图5-Z-4
5.如图5-Z-5,在△ABC中,AC的垂直平分线与AC,BC分别交于点E,D,CE=4,△ABC的周长是25,则△ABD的周长为
( )
A.13
B.15
C.17
D.19
图5-Z-5
6.在等腰三角形ABC中,AB=AC,AC边上的中线BD将这个三角形的周长分成15和12的两部分,则这个等腰三角形的底边长为
( )
A.7
B.11
C.7或11
D.7或10
二、填空题(每小题4分,共20分)
7.若等腰三角形的顶角为80°,则底角为 .?
8.在△ABC中,AD⊥BC于点D,且BD=CD,若AB=3,则AC= .?
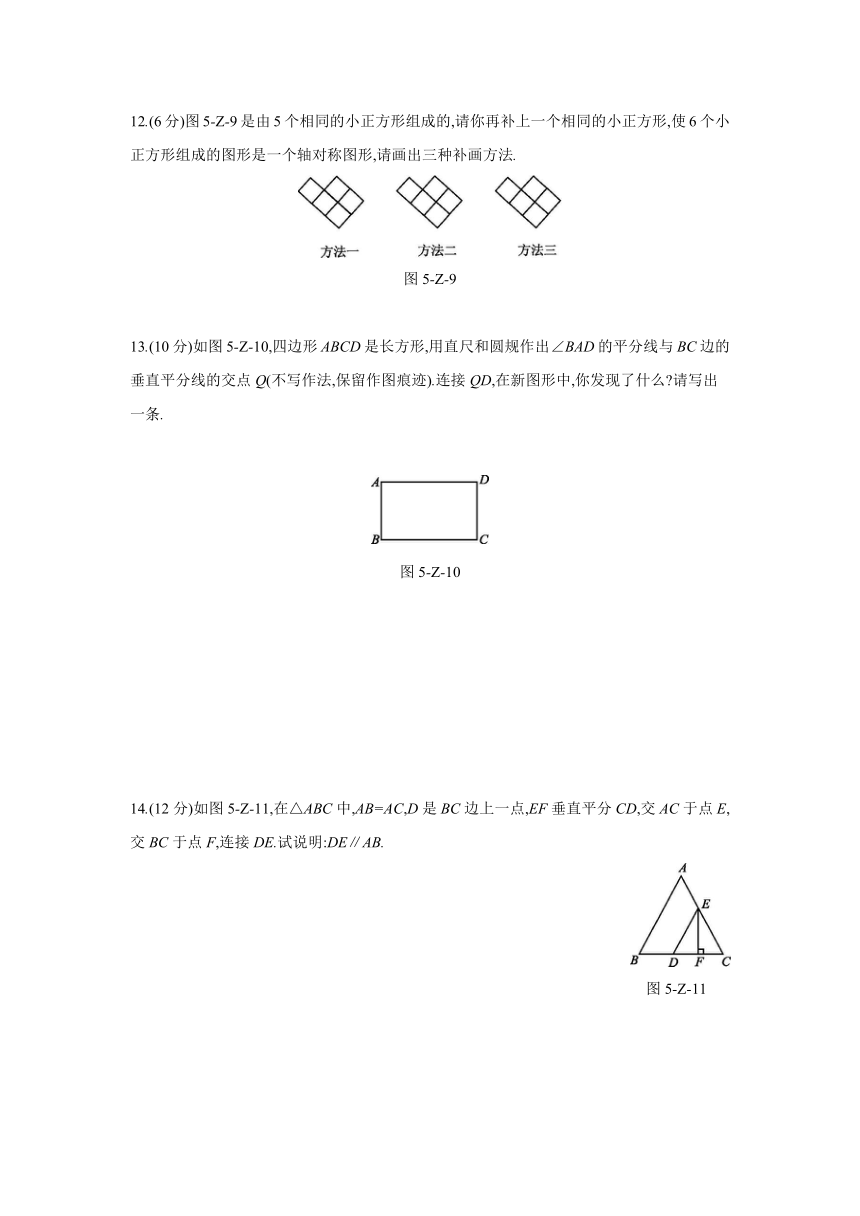
9.如图5-Z-6,在△ABC中,AB=AC,AD⊥BC于点D,E,F为AD上的两点,若△ABC的面积为12,则图中阴影部分的面积是 .?
图5-Z-6
10.如图5-Z-7,在△ABC中,D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE的度数为 .?
图5-Z-7
11.如图5-Z-8,在四边形ABCD中,∠A=90°,AD=8,对角线BD⊥CD,P是BC边上一动点,连接PD.若∠ADB=∠C,则PD长的最小值为 .?
图5-Z-8
三、解答题(共56分)
12.(6分)图5-Z-9是由5个相同的小正方形组成的,请你再补上一个相同的小正方形,使6个小正方形组成的图形是一个轴对称图形,请画出三种补画方法.
图5-Z-9
13.(10分)如图5-Z-10,四边形ABCD是长方形,用直尺和圆规作出∠BAD的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连接QD,在新图形中,你发现了什么?请写出
一条.
图5-Z-10
14.(12分)如图5-Z-11,在△ABC中,AB=AC,D是BC边上一点,EF垂直平分CD,交AC于点E,交BC于点F,连接DE.试说明:DE∥AB.
图5-Z-11
15.(14分)如图5-Z-12,在△ABC中,AC(1)如图①,已知边AB的垂直平分线与BC边交于点P,连接AP.试说明:∠APC=2∠B.
(2)如图②,以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
图5-Z-12
16.(14分)如图5-Z-13,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,OA,OB,OC.
(1)若△ADE的周长为6
cm,△OBC的周长为16
cm.
①求线段BC的长;
②求线段OA的长.
(2)若∠BAC=120°,求∠DAE的度数.
图5-Z-13
?
教师详解详析
1.B
2.D [解析]
由折叠的性质可知CB=EB,所以AE+CB=AE+EB=AB.故选D.
3.C [解析]
根据尺规作图可知OE是∠AOB的平分线.
A.OE是∠AOB的平分线,正确;
B.OC=OD,正确;
C.点C,D到OE的距离相等,不正确;
D.∠AOE=∠BOE,正确.
故选C.
4.B [解析]
因为AB=AC,∠A=40°,所以∠ABC=∠ACB=70°.因为CE平分∠ACB,所以
∠ACE=∠ACB=35°.因为BD⊥AC,所以∠ODC=90°,所以∠BOE=∠COD=180°-90°-35°=55°.
5.C
6.C [解析]
设腰长为2x,当3x=15时,腰为10,底为7;当3x=12时,腰为8,底为11.
故选C.
7.50°
8.3 [解析]
从已知得到AD是BC的垂直平分线,线段垂直平分线上的点到线段两个端点的距离相等.
9.6
10.20° [解析]
因为∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,所以
∠ADC=180°-∠ADB=180°-(180°-∠BAD-∠ABC)=40°+40°=80°,
∠ADE=∠ADB=180°-40°-40°=100°,所以∠CDE=100°-80°=20°.
11.8
12.解:答案不唯一,如图所示:
13.解:如图所示.
发现(不唯一):DQ=AQ或∠QAD=∠QDA等.
14.解:因为EF垂直平分CD,所以DE=CE,
所以∠EDC=∠C.
因为AB=AC,所以∠B=∠C,
所以∠B=∠EDC,所以DE∥AB.
15.解:(1)因为边AB的垂直平分线与BC边交于点P,
所以PA=PB,
所以∠B=∠BAP,则∠APB=180°-2∠B,
所以∠APC=180°-∠APB=180°-(180°-2∠B)=2∠B.
(2)根据题意可知BA=BQ,
所以∠BAQ=∠BQA,则2∠BQA=180°-∠B,即∠BQA=90°-∠B.
因为∠AQC=3∠B,所以∠AQC=180°-∠BQA=180°-90°-∠B,
所以3∠B=90°+∠B,所以∠B=36°.
16.解:(1)①因为l1是AB边的垂直平分线,
所以AD=BD.
因为l2是AC边的垂直平分线,
所以EA=EC,
所以BC=BD+DE+EC=AD+DE+EA=6
cm.
②因为l1是AB边的垂直平分线,
所以OA=OB.
因为l2是AC边的垂直平分线,所以OA=OC,所以OA=OB=OC.
因为△OBC的周长为16
cm,
所以OB+OC+BC=16
cm.
由①知,BC=6
cm,
所以OB=OC=5
cm,
所以OA=5
cm.
(2)因为∠BAC=120°,
所以∠ABC+∠ACB=60°.
因为AD=BD,EA=EC,
所以∠BAD=∠ABC,∠EAC=∠ACB,
所以∠DAE=∠BAC-∠BAD-∠EAC=∠BAC-∠ABC-∠ACB=60°.
[范围:第五章 生活中的轴对称 时间:40分钟 分值:100分]
一、选择题(每小题4分,共24分)
1.图5-Z-1中的轴对称图形是
( )
图5-Z-1
2.如图5-Z-2,将一张三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是
( )
A.AD=BC
B.AE=AC
C.ED+EB=DB
D.AE+CB=AB
图5-Z-2
3.观察图5-Z-3中尺规作图的痕迹,下列说法错误的是
( )
A.OE是∠AOB的平分线
B.OC=OD
C.点C,D到OE的距离不相等
D.∠AOE=∠BOE
图5-Z-3
4.如图5-Z-4,BD,CE分别是△ABC的高线和角平分线,且相交于点O.若AB=AC,∠A=40°,则∠BOE的度数是
( )
A.60°
B.55°
C.50°
D.40°
图5-Z-4
5.如图5-Z-5,在△ABC中,AC的垂直平分线与AC,BC分别交于点E,D,CE=4,△ABC的周长是25,则△ABD的周长为
( )
A.13
B.15
C.17
D.19
图5-Z-5
6.在等腰三角形ABC中,AB=AC,AC边上的中线BD将这个三角形的周长分成15和12的两部分,则这个等腰三角形的底边长为
( )
A.7
B.11
C.7或11
D.7或10
二、填空题(每小题4分,共20分)
7.若等腰三角形的顶角为80°,则底角为 .?
8.在△ABC中,AD⊥BC于点D,且BD=CD,若AB=3,则AC= .?
9.如图5-Z-6,在△ABC中,AB=AC,AD⊥BC于点D,E,F为AD上的两点,若△ABC的面积为12,则图中阴影部分的面积是 .?
图5-Z-6
10.如图5-Z-7,在△ABC中,D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE的度数为 .?
图5-Z-7
11.如图5-Z-8,在四边形ABCD中,∠A=90°,AD=8,对角线BD⊥CD,P是BC边上一动点,连接PD.若∠ADB=∠C,则PD长的最小值为 .?
图5-Z-8
三、解答题(共56分)
12.(6分)图5-Z-9是由5个相同的小正方形组成的,请你再补上一个相同的小正方形,使6个小正方形组成的图形是一个轴对称图形,请画出三种补画方法.
图5-Z-9
13.(10分)如图5-Z-10,四边形ABCD是长方形,用直尺和圆规作出∠BAD的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连接QD,在新图形中,你发现了什么?请写出
一条.
图5-Z-10
14.(12分)如图5-Z-11,在△ABC中,AB=AC,D是BC边上一点,EF垂直平分CD,交AC于点E,交BC于点F,连接DE.试说明:DE∥AB.
图5-Z-11
15.(14分)如图5-Z-12,在△ABC中,AC
(2)如图②,以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
图5-Z-12
16.(14分)如图5-Z-13,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,OA,OB,OC.
(1)若△ADE的周长为6
cm,△OBC的周长为16
cm.
①求线段BC的长;
②求线段OA的长.
(2)若∠BAC=120°,求∠DAE的度数.
图5-Z-13
?
教师详解详析
1.B
2.D [解析]
由折叠的性质可知CB=EB,所以AE+CB=AE+EB=AB.故选D.
3.C [解析]
根据尺规作图可知OE是∠AOB的平分线.
A.OE是∠AOB的平分线,正确;
B.OC=OD,正确;
C.点C,D到OE的距离相等,不正确;
D.∠AOE=∠BOE,正确.
故选C.
4.B [解析]
因为AB=AC,∠A=40°,所以∠ABC=∠ACB=70°.因为CE平分∠ACB,所以
∠ACE=∠ACB=35°.因为BD⊥AC,所以∠ODC=90°,所以∠BOE=∠COD=180°-90°-35°=55°.
5.C
6.C [解析]
设腰长为2x,当3x=15时,腰为10,底为7;当3x=12时,腰为8,底为11.
故选C.
7.50°
8.3 [解析]
从已知得到AD是BC的垂直平分线,线段垂直平分线上的点到线段两个端点的距离相等.
9.6
10.20° [解析]
因为∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,所以
∠ADC=180°-∠ADB=180°-(180°-∠BAD-∠ABC)=40°+40°=80°,
∠ADE=∠ADB=180°-40°-40°=100°,所以∠CDE=100°-80°=20°.
11.8
12.解:答案不唯一,如图所示:
13.解:如图所示.
发现(不唯一):DQ=AQ或∠QAD=∠QDA等.
14.解:因为EF垂直平分CD,所以DE=CE,
所以∠EDC=∠C.
因为AB=AC,所以∠B=∠C,
所以∠B=∠EDC,所以DE∥AB.
15.解:(1)因为边AB的垂直平分线与BC边交于点P,
所以PA=PB,
所以∠B=∠BAP,则∠APB=180°-2∠B,
所以∠APC=180°-∠APB=180°-(180°-2∠B)=2∠B.
(2)根据题意可知BA=BQ,
所以∠BAQ=∠BQA,则2∠BQA=180°-∠B,即∠BQA=90°-∠B.
因为∠AQC=3∠B,所以∠AQC=180°-∠BQA=180°-90°-∠B,
所以3∠B=90°+∠B,所以∠B=36°.
16.解:(1)①因为l1是AB边的垂直平分线,
所以AD=BD.
因为l2是AC边的垂直平分线,
所以EA=EC,
所以BC=BD+DE+EC=AD+DE+EA=6
cm.
②因为l1是AB边的垂直平分线,
所以OA=OB.
因为l2是AC边的垂直平分线,所以OA=OC,所以OA=OB=OC.
因为△OBC的周长为16
cm,
所以OB+OC+BC=16
cm.
由①知,BC=6
cm,
所以OB=OC=5
cm,
所以OA=5
cm.
(2)因为∠BAC=120°,
所以∠ABC+∠ACB=60°.
因为AD=BD,EA=EC,
所以∠BAD=∠ABC,∠EAC=∠ACB,
所以∠DAE=∠BAC-∠BAD-∠EAC=∠BAC-∠ABC-∠ACB=60°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
