2020-2021学年七年级数学北师大版下册单元检测试卷 第五章 生活中的轴对称(B卷)(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册单元检测试卷 第五章 生活中的轴对称(B卷)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 319.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 17:51:31 | ||
图片预览


文档简介
第五章综合提升卷
范围:生活中的轴对称 时间:90分钟 分值:100分
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
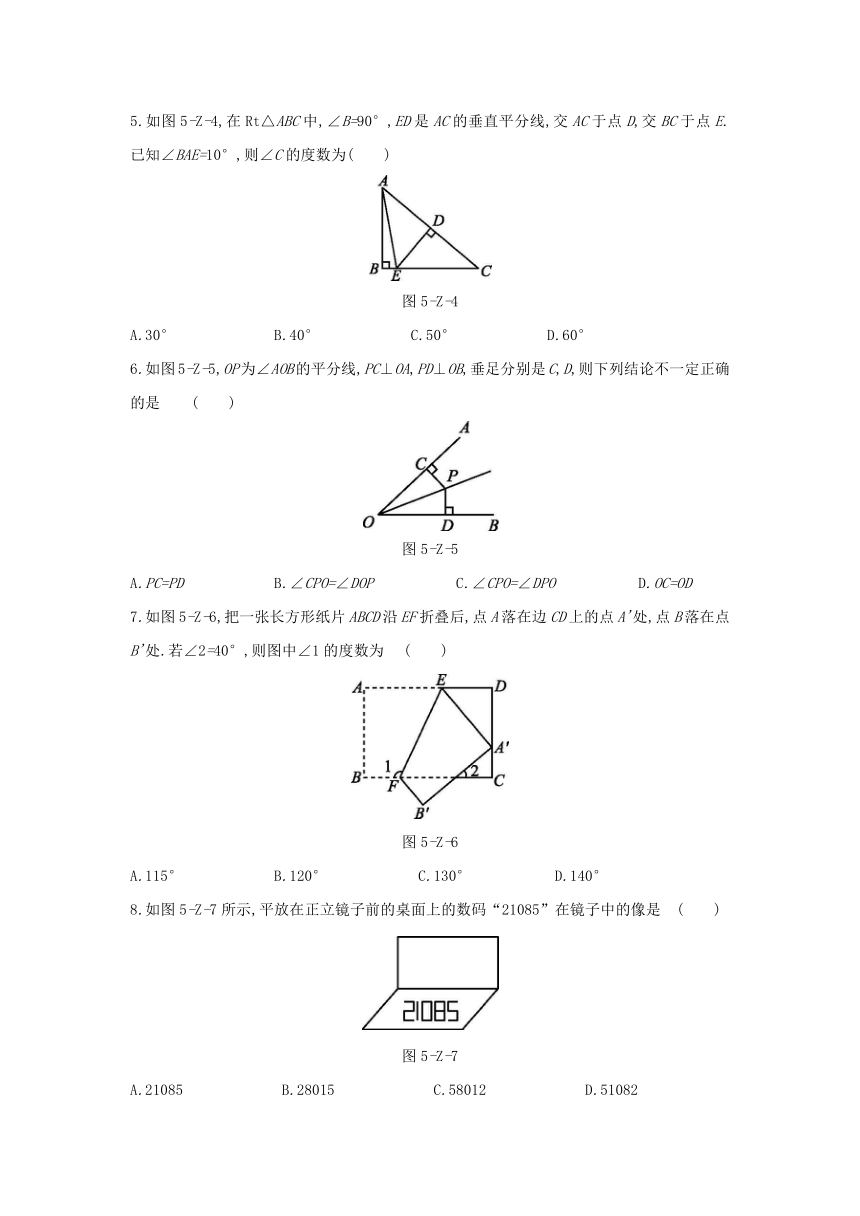
1.如图5-Z-1中的轴对称图形是
( )
图5-Z-1
2.下列说法正确的是
( )
A.两个全等的三角形合在一起是轴对称图形
B.轴对称图形至少有一条对称轴
C.线段不是轴对称图形
D.三角形的一条高就是它的对称轴
3.如图5-Z-2,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,CD=2,则点D到AB的距离是
( )
图5-Z-2
A.1
B.2
C.3
D.4
4.如图5-Z-3,△ABC与△A1B1C1关于直线MN对称,P为MN上任一点,则下列结论中错误的是( )
图5-Z-3
A.△AA1P是等腰三角形
B.MN垂直平分AA1,CC1
C.△ABC与△A1B1C1的面积相等
D.直线AB,A1B1的交点不一定在直线MN上
5.如图5-Z-4,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为( )
图5-Z-4
A.30°
B.40°
C.50°
D.60°
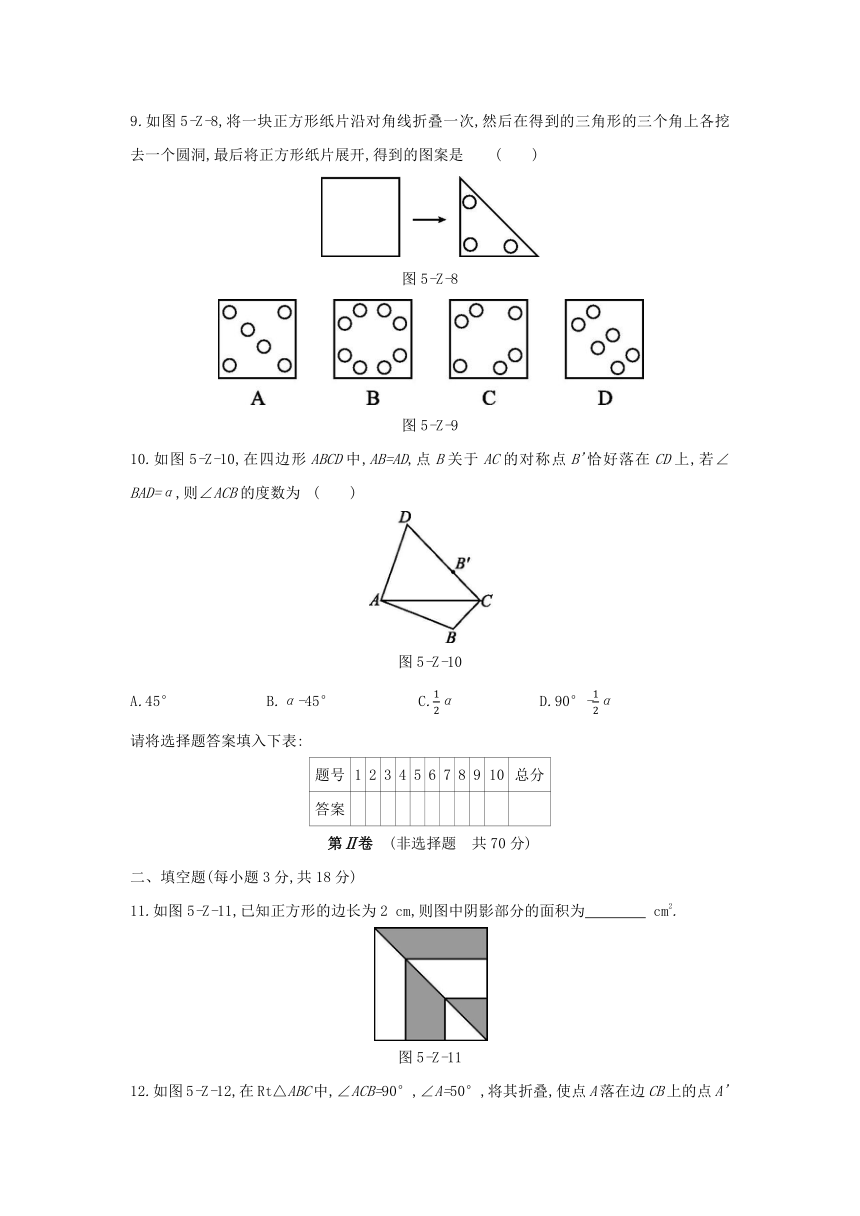
6.如图5-Z-5,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论不一定正确的是
( )
图5-Z-5
A.PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D.OC=OD
7.如图5-Z-6,把一张长方形纸片ABCD沿EF折叠后,点A落在边CD上的点A'处,点B落在点B'处.若∠2=40°,则图中∠1的度数为
( )
图5-Z-6
A.115°
B.120°
C.130°
D.140°
8.如图5-Z-7所示,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是
( )
图5-Z-7
A.21085
B.28015
C.58012
D.51082
9.如图5-Z-8,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是
( )
图5-Z-8
图5-Z-9
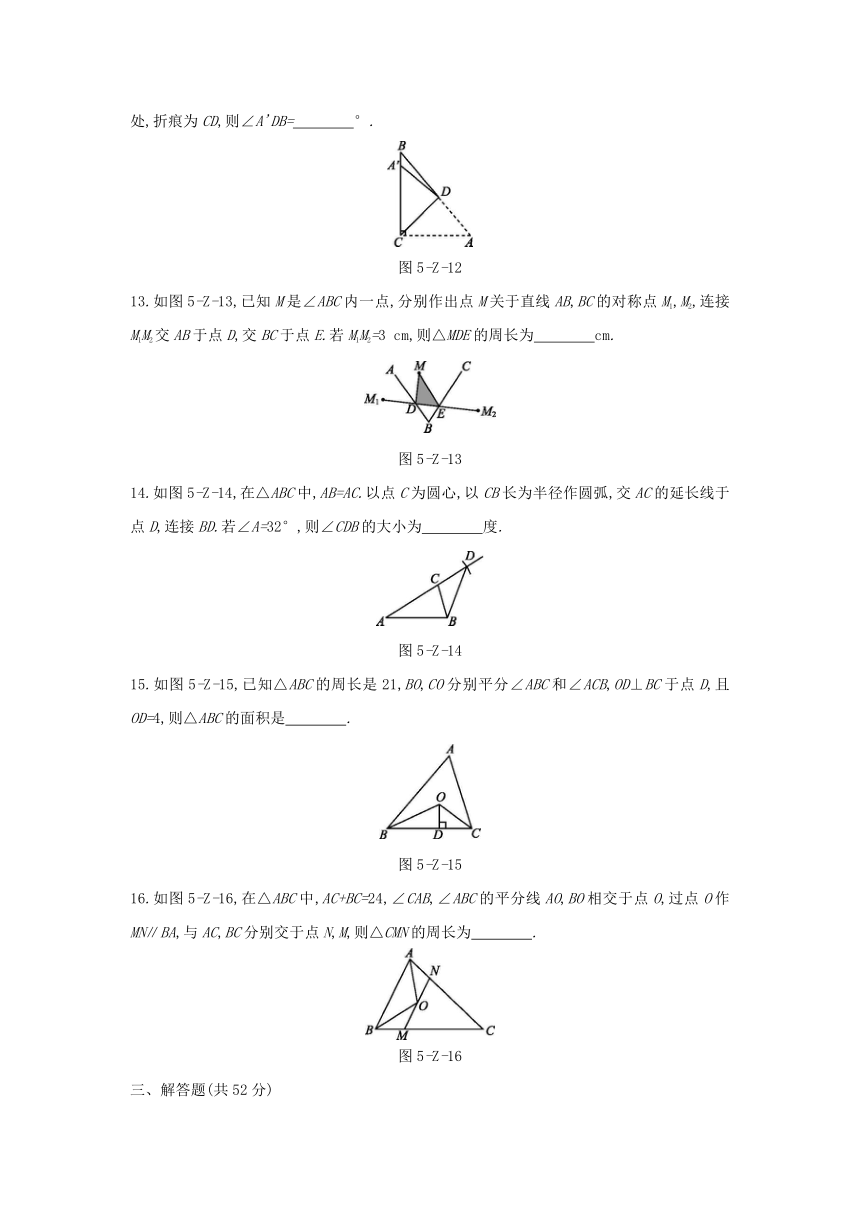
10.如图5-Z-10,在四边形ABCD中,AB=AD,点B关于AC的对称点B'恰好落在CD上,若∠BAD=α,则∠ACB的度数为
( )
图5-Z-10
A.45°
B.α-45°
C.α
D.90°-α
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷 (非选择题 共70分)
二、填空题(每小题3分,共18分)
11.如图5-Z-11,已知正方形的边长为2
cm,则图中阴影部分的面积为
cm2.?
图5-Z-11
12.如图5-Z-12,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的点A'处,折痕为CD,则∠A'DB= °.?
图5-Z-12
13.如图5-Z-13,已知M是∠ABC内一点,分别作出点M关于直线AB,BC的对称点M1,M2,连接M1M2交AB于点D,交BC于点E.若M1M2=3
cm,则△MDE的周长为 cm.?
图5-Z-13
14.如图5-Z-14,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连接BD.若∠A=32°,则∠CDB的大小为 度.?
图5-Z-14
15.如图5-Z-15,已知△ABC的周长是21,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4,则△ABC的面积是 .?
图5-Z-15
16.如图5-Z-16,在△ABC中,AC+BC=24,∠CAB,∠ABC的平分线AO,BO相交于点O,过点O作MN∥BA,与AC,BC分别交于点N,M,则△CMN的周长为 .?
图5-Z-16
三、解答题(共52分)
17.(4分)如图5-Z-17,阴影部分是由5个小正方形组成的一个直角图形,请用四种不同的方法分别在图中方格内再涂黑2个小正方形,使阴影部分组成的图形成为轴对称图形.
图5-Z-17
18.(6分)已知:如图5-Z-18,在等边三角形ABC中,D为BC延长线上的一点,E为CA延长线上的一点,且AE=DC.试说明:AD=BE.(提示:等边三角形的三个内角相等,均为60°)
图5-Z-18
19.(6分)如图5-Z-19所示,在△ABC中,AB=AC=5,AB的垂直平分线DE与AB,AC分别交于点E,D,连接BD.
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.
图5-Z-19
20.(6分)如图5-Z-20,已知∠BAC=90°,AD⊥BC于点D,交∠ABC的平分线于点E,F为AC上的一点,FG⊥BC于点G,FG=ED.试说明:AE=CF.
图5-Z-20
21.(6分)京九铁路贯穿某市,为该市的经济发展提供了巨大的商机,该市A,B两商业重镇的位置如图5-Z-21所示.市政府决定在铁路旁修建一物资中转站,以便A,B两商业重镇的产品及时调运.
(1)为了A,B两镇的公平,中转站应建在什么地方?
(2)为了节省修路的费用,中转站又应建在什么地方?
图5-Z-21
22.(8分)如图5-Z-22①,在△ABC中,AB=AC,D是BC的中点,点E在AD上.
(1)试说明:BE=CE;
(2)如图②,若BE的延长线交AC于点F,且BF⊥AC,AF=BF.试说明:△AEF≌△BCF.
图5-Z-22
23.(8分)如图5-Z-23,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.若AB=8
cm,△MBC的周长是14
cm.
(1)求BC的长.
(2)在直线MN上是否存在点P,使|PA-CP|的值最大?若存在,画出点P的位置,并求最大值;若不存在,说明理由.
图5-Z-23
24.(8分)如图5-Z-24,在△ABC中,点D在BC上,点E在BC的延长线上,且BD=BA,CE=CA.
(1)如图①,若∠BAC=90°,∠B=45°,试求∠DAE的度数;
(2)如图①,若∠BAC=90°,∠B=60°,则∠DAE的度数为 (直接写出结果);?
(3)如图②,若∠BAC>90°,其余条件不变,探究∠DAE与∠BAC之间有怎样的数量关系.
图5-Z-24
典题讲评与答案详析
第五章综合提升卷
1.B
2.B
3.B
4.D
5.B
6.B [解析]
A.由角平分线上的点到角的两边的距离相等,可知选项A正确.
B.因为OP为∠AOB的平分线,所以∠COP=∠DOP.因为∠COP与∠CPO不一定相等,所以∠CPO与∠DOP也不一定相等.故选项B错误.
C.因为PC⊥OA,PD⊥OB,所以∠PCO=∠PDO=90°.又因为∠COP=∠DOP,OP=OP,所以△COP≌△DOP(AAS),所以∠CPO=∠DPO.故选项C正确.
D.因为△COP≌△DOP,所以OC=OD.故选项D正确.故选B.
7.A [解析]
因为四边形ABCD是长方形,所以AD∥BC,∠C=∠D=∠A=90°.因为∠2=40°,所以∠B'A'C=90°-40°=50°.因为四边形ABFE与四边形A'B'FE全等,所以∠AEF=∠A'EF,∠B'A'E=∠A=90°,所以∠DA'E=180°-∠B'A'E-∠B'A'C=180°-90°-50°=40°.因为∠DA'E+∠D+∠DEA'=∠AEA'+∠DEA'=180°,所以∠AEA'=∠D+∠DA'E=90°+40°=130°,所以∠AEF+∠A'EF=130°,所以∠AEF=∠A'EF=65°.因为AD∥BC,所以∠1=180°-∠AEF=180°-65°=115°.故选A.
8.D
9.C
10.D [解析]
如图,连接AB',BB',过点A作AE⊥CD于点E.
因为点B关于AC的对称点B'恰好落在CD上,
所以AB=AB',∠BAC=∠B'AC,∠ACB=∠ACB'.
因为AB=AD,所以AD=AB'.
又因为AE⊥CD,所以∠DAE=∠B'AE,
所以∠CAE=∠BAD=α.
又因为∠AEB'=90°,
所以∠ACB=∠ACB'=90°-∠CAE=90°-α.
故选D.
11.2
12.10
13.3 [解析]
因为点M关于直线AB,BC的对称点分别为M1,M2,
所以EM=EM2,DM1=DM,
所以△MDE的周长=DE+EM+DM=M1M2=3
cm.
故答案为3.
14.37
15.42 [解析]
连接AO,利用角平分线上的点到角两边的距离相等,可知△AOB(以AB为底边),△AOC(以AC为底边),△BOC(以BC为底边)的高都为4,
所以S△ABC=S△AOB+S△AOC+S△BOC
=×4AB+×4AC+×4BC
=×4(AB+AC+BC)
=×4×21
=42.
16.24
17.解:如图所示:
18.解:在等边三角形ABC中,AB=CA,∠BAC=∠ACB=60°,
所以∠EAB=∠DCA=120°.
在△EAB和△DCA中,
因为AE=CD,∠EAB=∠DCA,AB=CA,
所以△EAB≌△DCA(SAS),所以AD=BE.
19.解:(1)因为D是AB垂直平分线上的点,
所以AD=BD.
因为△BCD的周长为8,即BD+CD+BC=8,
所以AD+CD+BC=8,
即AC+BC=8.
又因为AC=5,所以BC=3.
(2)因为BC=4,AC=5,所以△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC=9.
20.解:如图所示,过点E作EH⊥AB于点H.
因为BE平分∠ABC,EH⊥AB,ED⊥BC,
所以EH=ED(角平分线的性质).
又因为FG=ED,所以EH=FG.
因为∠BAD+∠CAD=90°,
∠C+∠CAD=90°,
所以∠BAD=∠C.
又因为∠AHE=∠CGF=90°,
所以△AEH≌△CFG,所以AE=CF.
21.解:(1)为了A,B两镇的公平,中转站到A,B的距离应相等,作AB的垂直平分线,与铁路所在直线的交点P即为中转站的位置,如图①.
(2)为了节省修路的费用,即中转站到A,B的距离之和最小,如图②,作点A关于铁路所在直线的对应点A',连接A'B,与铁路所在直线交于点P1,点P1即为中转站的位置.
22.解:(1)因为AB=AC,D是BC的中点,
所以∠BAE=∠CAE.
在△ABE和△ACE中,
因为AB=AC,∠BAE=∠CAE,AE=AE,
所以△ABE≌△ACE,
所以BE=CE.
(2)因为AB=AC,D是BC的中点,
所以AD⊥BC,
所以∠EAF+∠C=90°.
又因为BF⊥AC,
所以∠CBF+∠C=90°,
所以∠EAF=∠CBF.
在△AEF和△BCF中,
因为∠AFE=∠BFC=90°,AF=BF,∠EAF=∠CBF,
所以△AEF≌△BCF(ASA).
23.解:(1)因为MN垂直平分AB,所以MB=MA.又因为△MBC的周长是14
cm,所以MB+MC+BC=MA+MC+BC=AC+BC=14
cm.
因为AB=8
cm,所以BC=6
cm.
(2)存在.如图,当P是直线MN与BC延长线的交点时,|PA-CP|的值最大,最大值是6
cm.
理由:因为点A,B关于直线MN对称,所以AP=BP.当点P位于MN上(直线MN与BC延长线的交点除外)时,根据三角形三边关系始终有|PA-CP|=|PB-CP|cm,即|PA-CP|的最大值为6
cm.
24.解:(1)因为∠BAC=90°,∠B=45°,
所以∠ACB=45°,所以∠ACE=135°.
因为CE=AC,
所以∠CAE=∠E=(180°-∠ACE)=22.5°.
因为BA=BD,
所以∠BAD=∠ADB=×(180°-45°)=67.5°.
因为∠BAE=180°-∠B-∠E=180°-45°-22.5°=112.5°,
所以∠DAE=∠BAE-∠BAD=45°.
(2)因为∠BAC=90°,∠B=60°,
所以∠ACB=30°,所以∠ACE=150°.
因为CE=AC,
所以∠CAE=∠E=(180°-∠ACE)=15°.
因为BA=BD,
所以∠BAD=∠ADB=×(180°-60°)=60°.
因为∠BAE=180°-∠B-∠E=180°-60°-15°=105°,
所以∠DAE=∠BAE-∠BAD=45°.
故答案为45°.
(3)设∠BAC=α,∠B=β,
所以∠ACB=180°-α-β,
所以∠ACE=180°-∠ACB=α+β.
因为CE=AC,
所以∠CAE=∠E=(180°-∠ACE)=(180°-α-β)=90°--.
因为BA=BD,
所以∠BAD=∠ADB=(180°-β)=90°-β.
因为∠BAE=180°-∠B-∠E=180°-β-90°--=90°+-,
所以∠DAE=∠BAE-∠BAD=90°+--90°-=α,
所以∠BAC=2∠DAE.
范围:生活中的轴对称 时间:90分钟 分值:100分
第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.如图5-Z-1中的轴对称图形是
( )
图5-Z-1
2.下列说法正确的是
( )
A.两个全等的三角形合在一起是轴对称图形
B.轴对称图形至少有一条对称轴
C.线段不是轴对称图形
D.三角形的一条高就是它的对称轴
3.如图5-Z-2,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,CD=2,则点D到AB的距离是
( )
图5-Z-2
A.1
B.2
C.3
D.4
4.如图5-Z-3,△ABC与△A1B1C1关于直线MN对称,P为MN上任一点,则下列结论中错误的是( )
图5-Z-3
A.△AA1P是等腰三角形
B.MN垂直平分AA1,CC1
C.△ABC与△A1B1C1的面积相等
D.直线AB,A1B1的交点不一定在直线MN上
5.如图5-Z-4,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为( )
图5-Z-4
A.30°
B.40°
C.50°
D.60°
6.如图5-Z-5,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论不一定正确的是
( )
图5-Z-5
A.PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D.OC=OD
7.如图5-Z-6,把一张长方形纸片ABCD沿EF折叠后,点A落在边CD上的点A'处,点B落在点B'处.若∠2=40°,则图中∠1的度数为
( )
图5-Z-6
A.115°
B.120°
C.130°
D.140°
8.如图5-Z-7所示,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是
( )
图5-Z-7
A.21085
B.28015
C.58012
D.51082
9.如图5-Z-8,将一块正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是
( )
图5-Z-8
图5-Z-9
10.如图5-Z-10,在四边形ABCD中,AB=AD,点B关于AC的对称点B'恰好落在CD上,若∠BAD=α,则∠ACB的度数为
( )
图5-Z-10
A.45°
B.α-45°
C.α
D.90°-α
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷 (非选择题 共70分)
二、填空题(每小题3分,共18分)
11.如图5-Z-11,已知正方形的边长为2
cm,则图中阴影部分的面积为
cm2.?
图5-Z-11
12.如图5-Z-12,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的点A'处,折痕为CD,则∠A'DB= °.?
图5-Z-12
13.如图5-Z-13,已知M是∠ABC内一点,分别作出点M关于直线AB,BC的对称点M1,M2,连接M1M2交AB于点D,交BC于点E.若M1M2=3
cm,则△MDE的周长为 cm.?
图5-Z-13
14.如图5-Z-14,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连接BD.若∠A=32°,则∠CDB的大小为 度.?
图5-Z-14
15.如图5-Z-15,已知△ABC的周长是21,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4,则△ABC的面积是 .?
图5-Z-15
16.如图5-Z-16,在△ABC中,AC+BC=24,∠CAB,∠ABC的平分线AO,BO相交于点O,过点O作MN∥BA,与AC,BC分别交于点N,M,则△CMN的周长为 .?
图5-Z-16
三、解答题(共52分)
17.(4分)如图5-Z-17,阴影部分是由5个小正方形组成的一个直角图形,请用四种不同的方法分别在图中方格内再涂黑2个小正方形,使阴影部分组成的图形成为轴对称图形.
图5-Z-17
18.(6分)已知:如图5-Z-18,在等边三角形ABC中,D为BC延长线上的一点,E为CA延长线上的一点,且AE=DC.试说明:AD=BE.(提示:等边三角形的三个内角相等,均为60°)
图5-Z-18
19.(6分)如图5-Z-19所示,在△ABC中,AB=AC=5,AB的垂直平分线DE与AB,AC分别交于点E,D,连接BD.
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.
图5-Z-19
20.(6分)如图5-Z-20,已知∠BAC=90°,AD⊥BC于点D,交∠ABC的平分线于点E,F为AC上的一点,FG⊥BC于点G,FG=ED.试说明:AE=CF.
图5-Z-20
21.(6分)京九铁路贯穿某市,为该市的经济发展提供了巨大的商机,该市A,B两商业重镇的位置如图5-Z-21所示.市政府决定在铁路旁修建一物资中转站,以便A,B两商业重镇的产品及时调运.
(1)为了A,B两镇的公平,中转站应建在什么地方?
(2)为了节省修路的费用,中转站又应建在什么地方?
图5-Z-21
22.(8分)如图5-Z-22①,在△ABC中,AB=AC,D是BC的中点,点E在AD上.
(1)试说明:BE=CE;
(2)如图②,若BE的延长线交AC于点F,且BF⊥AC,AF=BF.试说明:△AEF≌△BCF.
图5-Z-22
23.(8分)如图5-Z-23,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.若AB=8
cm,△MBC的周长是14
cm.
(1)求BC的长.
(2)在直线MN上是否存在点P,使|PA-CP|的值最大?若存在,画出点P的位置,并求最大值;若不存在,说明理由.
图5-Z-23
24.(8分)如图5-Z-24,在△ABC中,点D在BC上,点E在BC的延长线上,且BD=BA,CE=CA.
(1)如图①,若∠BAC=90°,∠B=45°,试求∠DAE的度数;
(2)如图①,若∠BAC=90°,∠B=60°,则∠DAE的度数为 (直接写出结果);?
(3)如图②,若∠BAC>90°,其余条件不变,探究∠DAE与∠BAC之间有怎样的数量关系.
图5-Z-24
典题讲评与答案详析
第五章综合提升卷
1.B
2.B
3.B
4.D
5.B
6.B [解析]
A.由角平分线上的点到角的两边的距离相等,可知选项A正确.
B.因为OP为∠AOB的平分线,所以∠COP=∠DOP.因为∠COP与∠CPO不一定相等,所以∠CPO与∠DOP也不一定相等.故选项B错误.
C.因为PC⊥OA,PD⊥OB,所以∠PCO=∠PDO=90°.又因为∠COP=∠DOP,OP=OP,所以△COP≌△DOP(AAS),所以∠CPO=∠DPO.故选项C正确.
D.因为△COP≌△DOP,所以OC=OD.故选项D正确.故选B.
7.A [解析]
因为四边形ABCD是长方形,所以AD∥BC,∠C=∠D=∠A=90°.因为∠2=40°,所以∠B'A'C=90°-40°=50°.因为四边形ABFE与四边形A'B'FE全等,所以∠AEF=∠A'EF,∠B'A'E=∠A=90°,所以∠DA'E=180°-∠B'A'E-∠B'A'C=180°-90°-50°=40°.因为∠DA'E+∠D+∠DEA'=∠AEA'+∠DEA'=180°,所以∠AEA'=∠D+∠DA'E=90°+40°=130°,所以∠AEF+∠A'EF=130°,所以∠AEF=∠A'EF=65°.因为AD∥BC,所以∠1=180°-∠AEF=180°-65°=115°.故选A.
8.D
9.C
10.D [解析]
如图,连接AB',BB',过点A作AE⊥CD于点E.
因为点B关于AC的对称点B'恰好落在CD上,
所以AB=AB',∠BAC=∠B'AC,∠ACB=∠ACB'.
因为AB=AD,所以AD=AB'.
又因为AE⊥CD,所以∠DAE=∠B'AE,
所以∠CAE=∠BAD=α.
又因为∠AEB'=90°,
所以∠ACB=∠ACB'=90°-∠CAE=90°-α.
故选D.
11.2
12.10
13.3 [解析]
因为点M关于直线AB,BC的对称点分别为M1,M2,
所以EM=EM2,DM1=DM,
所以△MDE的周长=DE+EM+DM=M1M2=3
cm.
故答案为3.
14.37
15.42 [解析]
连接AO,利用角平分线上的点到角两边的距离相等,可知△AOB(以AB为底边),△AOC(以AC为底边),△BOC(以BC为底边)的高都为4,
所以S△ABC=S△AOB+S△AOC+S△BOC
=×4AB+×4AC+×4BC
=×4(AB+AC+BC)
=×4×21
=42.
16.24
17.解:如图所示:
18.解:在等边三角形ABC中,AB=CA,∠BAC=∠ACB=60°,
所以∠EAB=∠DCA=120°.
在△EAB和△DCA中,
因为AE=CD,∠EAB=∠DCA,AB=CA,
所以△EAB≌△DCA(SAS),所以AD=BE.
19.解:(1)因为D是AB垂直平分线上的点,
所以AD=BD.
因为△BCD的周长为8,即BD+CD+BC=8,
所以AD+CD+BC=8,
即AC+BC=8.
又因为AC=5,所以BC=3.
(2)因为BC=4,AC=5,所以△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC=9.
20.解:如图所示,过点E作EH⊥AB于点H.
因为BE平分∠ABC,EH⊥AB,ED⊥BC,
所以EH=ED(角平分线的性质).
又因为FG=ED,所以EH=FG.
因为∠BAD+∠CAD=90°,
∠C+∠CAD=90°,
所以∠BAD=∠C.
又因为∠AHE=∠CGF=90°,
所以△AEH≌△CFG,所以AE=CF.
21.解:(1)为了A,B两镇的公平,中转站到A,B的距离应相等,作AB的垂直平分线,与铁路所在直线的交点P即为中转站的位置,如图①.
(2)为了节省修路的费用,即中转站到A,B的距离之和最小,如图②,作点A关于铁路所在直线的对应点A',连接A'B,与铁路所在直线交于点P1,点P1即为中转站的位置.
22.解:(1)因为AB=AC,D是BC的中点,
所以∠BAE=∠CAE.
在△ABE和△ACE中,
因为AB=AC,∠BAE=∠CAE,AE=AE,
所以△ABE≌△ACE,
所以BE=CE.
(2)因为AB=AC,D是BC的中点,
所以AD⊥BC,
所以∠EAF+∠C=90°.
又因为BF⊥AC,
所以∠CBF+∠C=90°,
所以∠EAF=∠CBF.
在△AEF和△BCF中,
因为∠AFE=∠BFC=90°,AF=BF,∠EAF=∠CBF,
所以△AEF≌△BCF(ASA).
23.解:(1)因为MN垂直平分AB,所以MB=MA.又因为△MBC的周长是14
cm,所以MB+MC+BC=MA+MC+BC=AC+BC=14
cm.
因为AB=8
cm,所以BC=6
cm.
(2)存在.如图,当P是直线MN与BC延长线的交点时,|PA-CP|的值最大,最大值是6
cm.
理由:因为点A,B关于直线MN对称,所以AP=BP.当点P位于MN上(直线MN与BC延长线的交点除外)时,根据三角形三边关系始终有|PA-CP|=|PB-CP|
cm.
24.解:(1)因为∠BAC=90°,∠B=45°,
所以∠ACB=45°,所以∠ACE=135°.
因为CE=AC,
所以∠CAE=∠E=(180°-∠ACE)=22.5°.
因为BA=BD,
所以∠BAD=∠ADB=×(180°-45°)=67.5°.
因为∠BAE=180°-∠B-∠E=180°-45°-22.5°=112.5°,
所以∠DAE=∠BAE-∠BAD=45°.
(2)因为∠BAC=90°,∠B=60°,
所以∠ACB=30°,所以∠ACE=150°.
因为CE=AC,
所以∠CAE=∠E=(180°-∠ACE)=15°.
因为BA=BD,
所以∠BAD=∠ADB=×(180°-60°)=60°.
因为∠BAE=180°-∠B-∠E=180°-60°-15°=105°,
所以∠DAE=∠BAE-∠BAD=45°.
故答案为45°.
(3)设∠BAC=α,∠B=β,
所以∠ACB=180°-α-β,
所以∠ACE=180°-∠ACB=α+β.
因为CE=AC,
所以∠CAE=∠E=(180°-∠ACE)=(180°-α-β)=90°--.
因为BA=BD,
所以∠BAD=∠ADB=(180°-β)=90°-β.
因为∠BAE=180°-∠B-∠E=180°-β-90°--=90°+-,
所以∠DAE=∠BAE-∠BAD=90°+--90°-=α,
所以∠BAC=2∠DAE.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
