流程图2
图片预览




文档简介
(共19张PPT)
第三课时.流程图(2)
开 始
输入n
计算 的值
>2012
使
n
的
值
增
加
1
输出n
结 束
Y
N
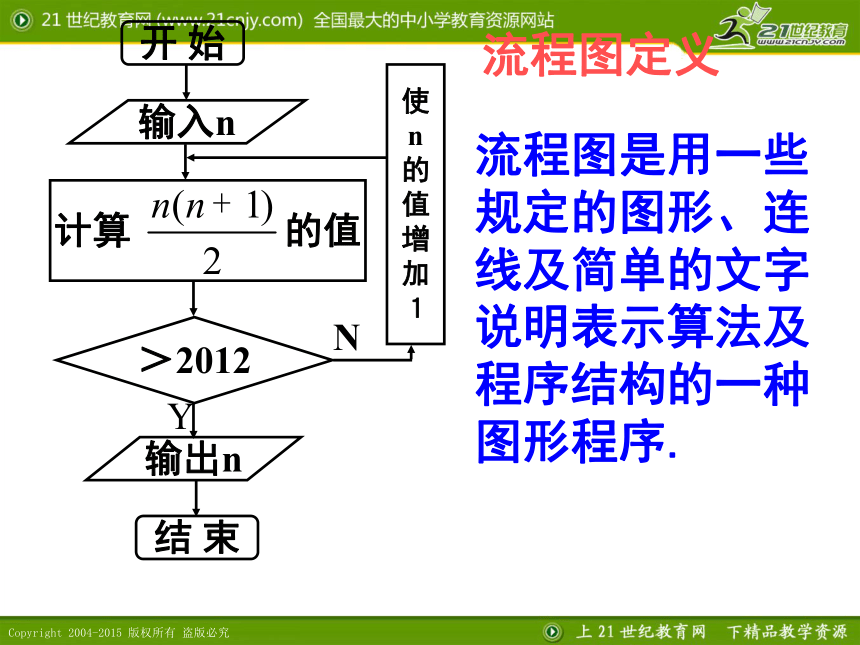
流程图定义
流程图是用一些规定的图形、连线及简单的文字说明表示算法及程序结构的一种图形程序.
程序框 名称 功能
起止框
表示一个算法的起始和结束
输入、
输出框
表示一个算法输入和输出的信息
赋值、计算
处理框
程序框 名称 功能
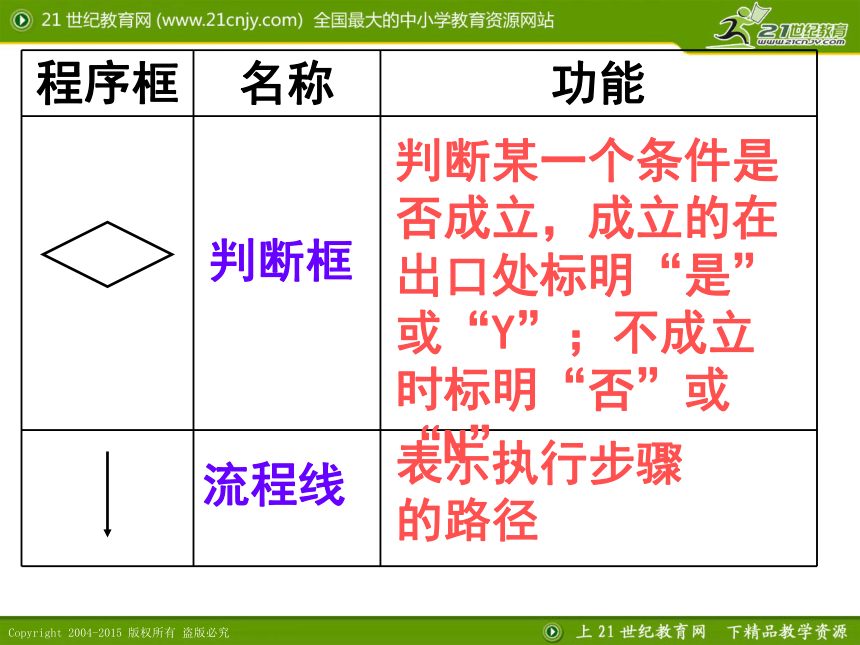
判断框
判断某一个条件是否成立,成立的在出口处标明“是”或“Y”;不成立时标明“否”或“N”
流程线
表示执行步骤的路径
算法都可以由顺序结构、选择结构、循环结构这三块“积木”通过组合和嵌套表达出来.
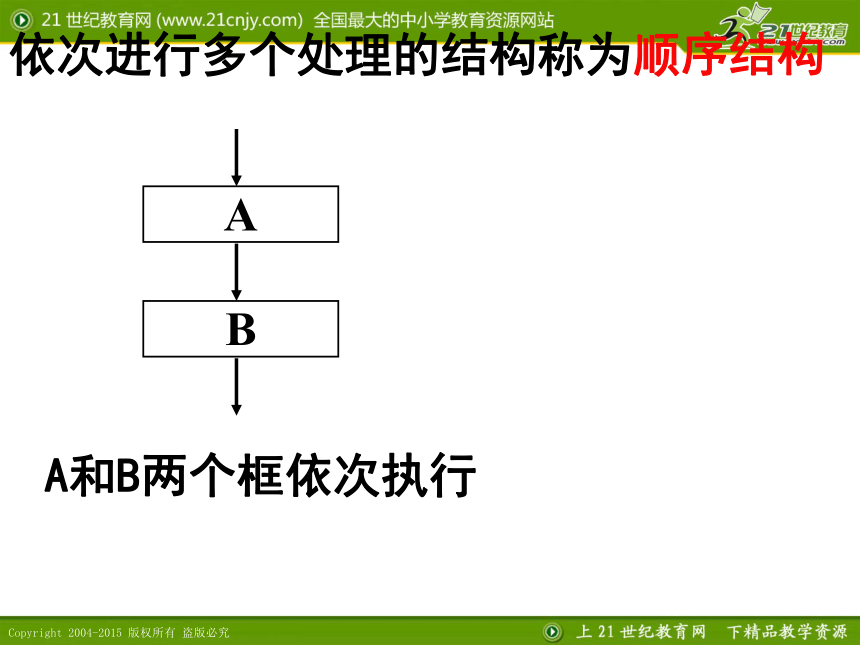
依次进行多个处理的结构称为顺序结构
A和B两个框依次执行
A
B
一、问题情境
问题1 已知两点(x1,y1),(x2,y2),求过两点的直线的斜率.用流程图表示解决上面问题的一个算法如下:
k←
结束
输入x1,y1,x2,y2
输出k
开始
上面的流程图对吗?
y2-y1
X2-x1
正确的算法应是:
S1 输入x1,y1,x2,y2的值;
S2 当x1≠x2时,
计算k= ,输出k的值;
否则输出“斜率不存在”.
y2-y1
X2-x1
那么如何在流程图中实现呢?
就需要加入判断的部分.
k←
输入x1,y1,x2,y2
输出k
x1≠x2
结束
Y
N
输出“斜率不存在”
开始
X2-x1
y2-y1
问题1中的流程图应是
二、数学理论
1、选择结构的概念:
先根据条件作出判断,再决定执行哪一种操作的结构.
2、选择结构的一般形式:
在选择结构中,含一个判断框,当条件p成立时,
执行A;否则执行B.
说明 在上面的选择结构中,只能执行A,B中的一个,不
可能两个都执行;两个框中可以有一个是空的,即不执行
任何操作.
p
A
B
Y
N
选择结构也叫分支结构
1.某铁路客运部门规定甲、乙两地之间旅客托运行李的
费用为
其中w(单位:kg)为行李的重量. 计算费用c(单位:元)的
算法可以用怎样的算法结构来表示
解:其算法为:
否则
S3 输出行李重量w和运费c.
上述算法用流程图表示如图所示.
三、数学应用
S 1 输入行李的重量w;
S2 如果w≤50,那么
练 某市出租汽车最新计费标准如下:在3km以内(含3km)路程按起步价8元收费,超过3km以外的路程按2.4元/km收费. 试给出一个出租车计费的算法.
分析:出租车收费y(元)和行驶里程x(km)之间的函数关系为:
解:算法步骤如下:
S1 输入里程x;
S2 若x≤3;则y←8,
否则 y←2.4(x-3)+8;
S3 输出y .
y ←8
结束
输出y
y←2.4(x-3)+8
开始
输入x
x≤3
Y
N
判断框:判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”.
例. 设计解一元二次方程ax2+bx+c=0(a≠0)的一个算法,并用流程图表示.
解:算法步骤如下:
S1 输入a,b,c;
S2 △←b2-4ac;
S3 若△<0;则输出“方程
无实数解”, 否则
,
,
输出x1, x2.
输出x1,x2
△<0
Y
N
开始
输入a,b,c
△←b2-4ac
注意:输出的文字应加上引号!
输出“方程无实数解”
结束
探究一:如果没有给出条件a≠0,那么如何设计算法?
例2. 设计解一元二次方程ax2+bx+c=0(a≠0)
的一个算法,并用流程图表示.
S1 若b=0,则执行S4,
否则执行S2;
S2
S3 输出x ,结束;
S4 若c=0,输出“方程有无数个解” ,结束,否则输出“方程无解”;
输出x
N
b=0
Y
c=0
N
Y
输出“方
程有无数
个解”
输出“方
程无解”
开始
输入a,b,c
Y
N
a=0
练习1
如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法过程。
开始
输入n
n ≥60
输出”及格”
输出”不及格”
结 束
Y
N
练习2
任意给定三个正实数,设计一个算法,判断:以这样三个数为边长的三角形是否存在?画出它的框图。
开始
输入a,b,c
a+b>c且b+c>a且c+a>b
输出”能构成三角形”
输出”不能构成三角形”
结束
Y
N
练习3
下面的流程图表示了一个什么样的算法?(图见讲义练习3)
【答】:输出a,b,c中最大的数。
思考:如果要实现上述流程图所表示的目的,是否还有其它的算法?
算法思路:将a与b进行比较,将大的数放入一个临时变量Max中,再将Max与c比较,输出大的数。
作业:
1.教案;
2.订正加复习.
第三课时.流程图(2)
开 始
输入n
计算 的值
>2012
使
n
的
值
增
加
1
输出n
结 束
Y
N
流程图定义
流程图是用一些规定的图形、连线及简单的文字说明表示算法及程序结构的一种图形程序.
程序框 名称 功能
起止框
表示一个算法的起始和结束
输入、
输出框
表示一个算法输入和输出的信息
赋值、计算
处理框
程序框 名称 功能
判断框
判断某一个条件是否成立,成立的在出口处标明“是”或“Y”;不成立时标明“否”或“N”
流程线
表示执行步骤的路径
算法都可以由顺序结构、选择结构、循环结构这三块“积木”通过组合和嵌套表达出来.
依次进行多个处理的结构称为顺序结构
A和B两个框依次执行
A
B
一、问题情境
问题1 已知两点(x1,y1),(x2,y2),求过两点的直线的斜率.用流程图表示解决上面问题的一个算法如下:
k←
结束
输入x1,y1,x2,y2
输出k
开始
上面的流程图对吗?
y2-y1
X2-x1
正确的算法应是:
S1 输入x1,y1,x2,y2的值;
S2 当x1≠x2时,
计算k= ,输出k的值;
否则输出“斜率不存在”.
y2-y1
X2-x1
那么如何在流程图中实现呢?
就需要加入判断的部分.
k←
输入x1,y1,x2,y2
输出k
x1≠x2
结束
Y
N
输出“斜率不存在”
开始
X2-x1
y2-y1
问题1中的流程图应是
二、数学理论
1、选择结构的概念:
先根据条件作出判断,再决定执行哪一种操作的结构.
2、选择结构的一般形式:
在选择结构中,含一个判断框,当条件p成立时,
执行A;否则执行B.
说明 在上面的选择结构中,只能执行A,B中的一个,不
可能两个都执行;两个框中可以有一个是空的,即不执行
任何操作.
p
A
B
Y
N
选择结构也叫分支结构
1.某铁路客运部门规定甲、乙两地之间旅客托运行李的
费用为
其中w(单位:kg)为行李的重量. 计算费用c(单位:元)的
算法可以用怎样的算法结构来表示
解:其算法为:
否则
S3 输出行李重量w和运费c.
上述算法用流程图表示如图所示.
三、数学应用
S 1 输入行李的重量w;
S2 如果w≤50,那么
练 某市出租汽车最新计费标准如下:在3km以内(含3km)路程按起步价8元收费,超过3km以外的路程按2.4元/km收费. 试给出一个出租车计费的算法.
分析:出租车收费y(元)和行驶里程x(km)之间的函数关系为:
解:算法步骤如下:
S1 输入里程x;
S2 若x≤3;则y←8,
否则 y←2.4(x-3)+8;
S3 输出y .
y ←8
结束
输出y
y←2.4(x-3)+8
开始
输入x
x≤3
Y
N
判断框:判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”.
例. 设计解一元二次方程ax2+bx+c=0(a≠0)的一个算法,并用流程图表示.
解:算法步骤如下:
S1 输入a,b,c;
S2 △←b2-4ac;
S3 若△<0;则输出“方程
无实数解”, 否则
,
,
输出x1, x2.
输出x1,x2
△<0
Y
N
开始
输入a,b,c
△←b2-4ac
注意:输出的文字应加上引号!
输出“方程无实数解”
结束
探究一:如果没有给出条件a≠0,那么如何设计算法?
例2. 设计解一元二次方程ax2+bx+c=0(a≠0)
的一个算法,并用流程图表示.
S1 若b=0,则执行S4,
否则执行S2;
S2
S3 输出x ,结束;
S4 若c=0,输出“方程有无数个解” ,结束,否则输出“方程无解”;
输出x
N
b=0
Y
c=0
N
Y
输出“方
程有无数
个解”
输出“方
程无解”
开始
输入a,b,c
Y
N
a=0
练习1
如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法过程。
开始
输入n
n ≥60
输出”及格”
输出”不及格”
结 束
Y
N
练习2
任意给定三个正实数,设计一个算法,判断:以这样三个数为边长的三角形是否存在?画出它的框图。
开始
输入a,b,c
a+b>c且b+c>a且c+a>b
输出”能构成三角形”
输出”不能构成三角形”
结束
Y
N
练习3
下面的流程图表示了一个什么样的算法?(图见讲义练习3)
【答】:输出a,b,c中最大的数。
思考:如果要实现上述流程图所表示的目的,是否还有其它的算法?
算法思路:将a与b进行比较,将大的数放入一个临时变量Max中,再将Max与c比较,输出大的数。
作业:
1.教案;
2.订正加复习.
