流程图复习课
图片预览








文档简介
(共33张PPT)
流程图(3)----循环结构
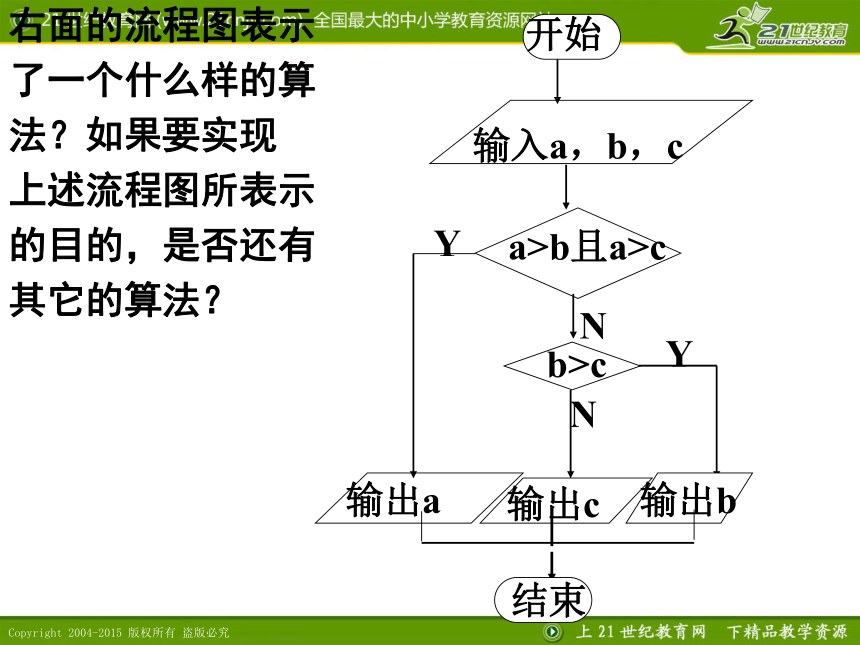
开始
输入a,b,c
a>b且a>c
b>c
Y
N
Y
N
输出a
输出c
输出b
结束
右面的流程图表示了一个什么样的算法?如果要实现
上述流程图所表示的目的,是否还有其它的算法?
结束
输出S
S ←
开始
S← S +i
i ← i +
Y
N
i ←
0
开始
S ←
结束
输出S
i←
S←S+i
i←i+
N
Y
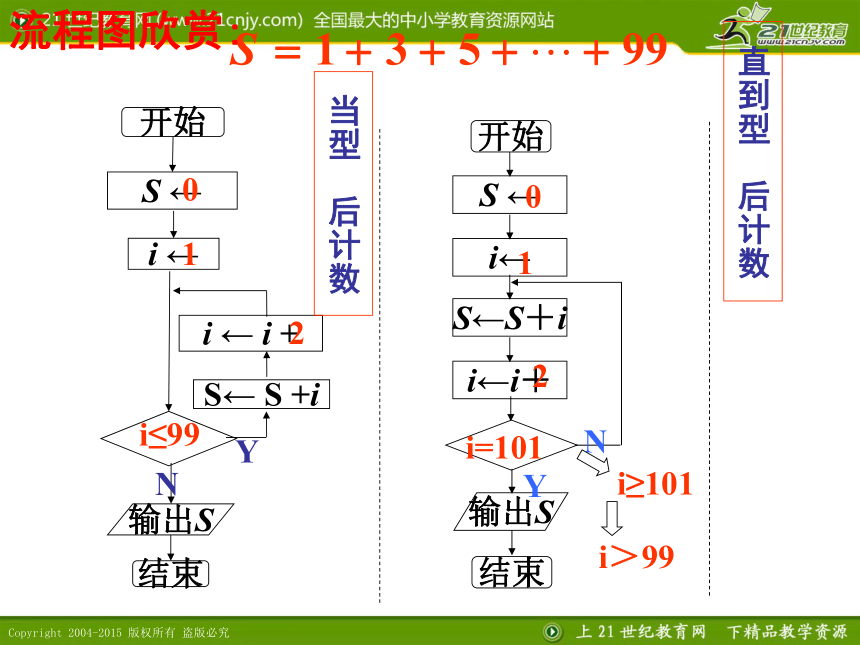
当型 后计数
直到型 后计数
0
1
2
2
1
i≤99
i=101
i≥101
i>99
流程图欣赏:
结束
输出S
S ←
开始
i ← i +
S ← S +i
Y
N
i ←
开始
S ←
结束
输出S
i←
i←i+
S←S+i
N
Y
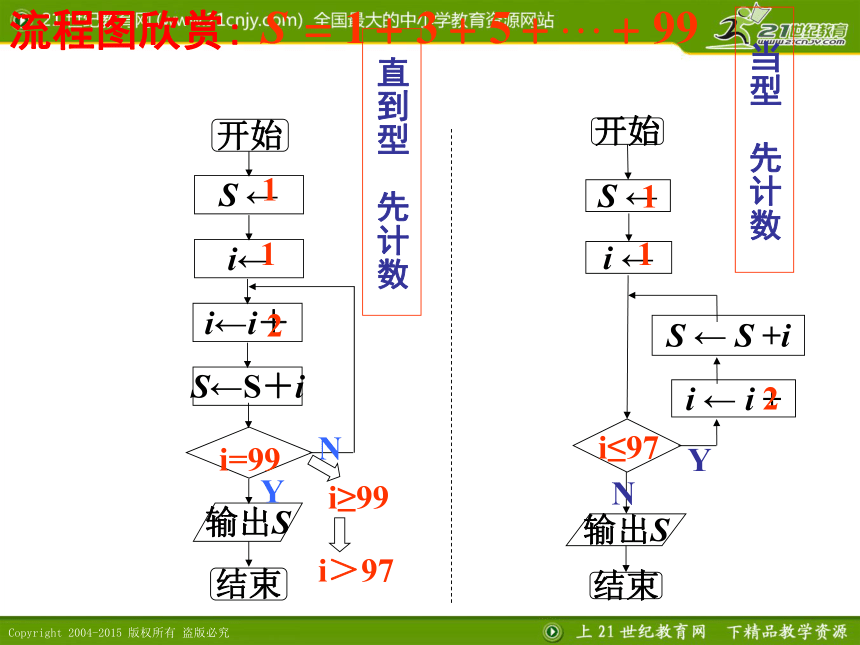
直到型 先计数
当型 先计数
1
1
2
2
1
1
i=99
i≤97
i≥99
i>97
流程图欣赏:
1.算法的基本逻辑结构有三种,即顺序结构、条件结构和循环结构。
其中顺序结构是最简单的结构,也是最基本的结构,循环结构必然包含条件结构,所以这三种基本逻辑结构是相互支撑的,无论怎样复杂的逻辑结构,都可以通过这三种结构来表达 。
3.在循环结构中都有一个计数变量和累加变量。计数变量用于记录循环次数,累加变量用于输出结果。计数变量和累加变量一般是同步执行的,累加一次,计数一次。
2.循环结构要在某个条件下终止循环,这就需要条件结构来判断。因此,循环结构中一定包含条件结构,但不允许“死循环”。
循环结构的三要素
循环变量,循环体、循环的终止条件。
4.画循环结构流程图前:
①确定循环变量和初始条件;
②确定算法中反复执行的部分,即循环体;
③确定循环的转向位置;
④确定循环的终止条件.
【课堂互动●例题】
解:算法如下: S1 输入a,b; S2 r←mod(a,b); q←(a r)/b; S3 输出q,r; S4 结束.
例1.写出求两个正整数a与b相除所得的商q及余数r的一个算法,并画出流程图.(提示:用mod(a,b)表示a除以b所得的余数)
流程框图为
r←mod(a,b)
q←(a r)/b
输出q,r
输入a,b
开始
结束
【课堂互动●例题】
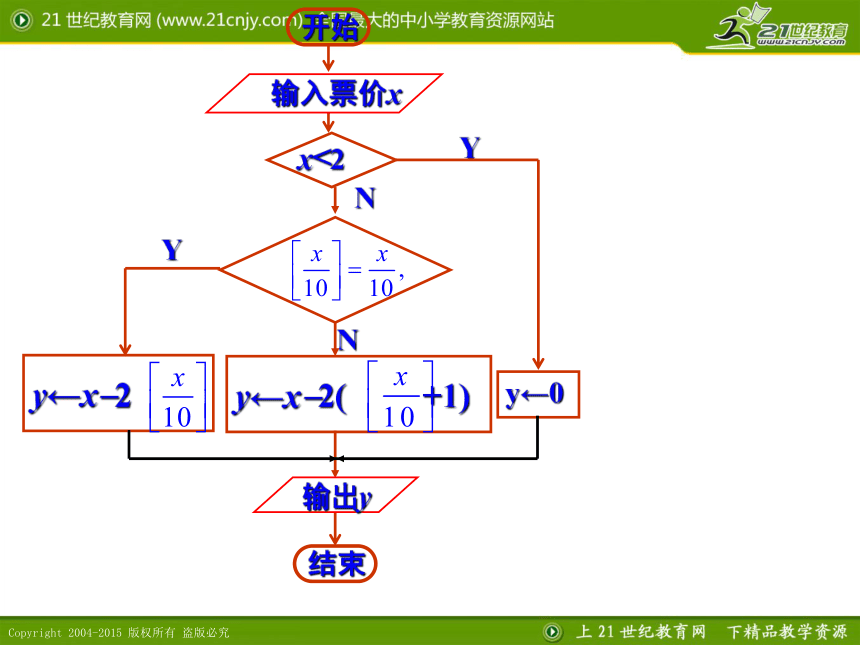
解:算法如下: S1 输入票价x; S2 如果x<2那么y=0,否则如果 那么y=x 2 否则y=x 2( +1), S3 输出返还金额y; S4 结束.
流程框图为
例2.火车站对乘客在一定时段内退票要收取一定的费用,收费的办法是:按票价每10元(不足10元按10元计算)核收2元,票价在2元以下的不退.试分步写出将票价为x元的车票退掉后,返还的金额y元的算法,并画出流程图.
Y
N
y←0
输出y
输入票价x
x<2
y←x 2
y←x 2( +1)
Y
N
开始
结束
例3.写出在数3,5,8,9,12,15,35,7,18,52中搜索数18的一个算法,并画出流程图.
【课堂互动●例题】
开始
输入n
n=18
N
输出n
结束
Y
解:算法如下: S1 输入n; S2 如果n=18,则转S3, 否则转S1 S3 输出n; S4 结束.
例4.写出求
(共有6个2)的值的一个算法,并画出流程图.
开始
I←1
I≥6
Y
输出S
结束
S←1/2
I←I+1
S←1/(2+S)
N
解:算法如下: S1 S← ; S2 I←1; S3 S← ,I←I+1; S4 如果I 小于6,那么转S3 S5 输出S; S6 结束.
解:S1 T←0;
S2 I←1;
S5 I←I+1,转S3;
S3 如果I≤100,那么转S4,
否则转S6;
S4 T←T+1/I;
S6 输出T.
【学生活动】
设计计算 ,的一个算法, 并画出流程图 .
开始
I≤100
Y
N
结束
T←1
I←I+1
输出T
I←1
T←T+1/I
开始
I≤100
Y
N
结束
T←1
I←I+1
输出T
I←1
T←T+1/I
【学生练习】请说出下列程序框图表示的算法功能:
T≥10000
Y
N
T←1
I←I+3
输出I
I←3
T←T×I
开始
结束
1+2+3+…+n>2010.
3.退出循环的条件是什么?
1.你准备用哪种循环
例3:请设计一个算法计算满足下列不等式的最小正数n.
2.你认为如何设计累加变量和计数器的初始值比较合适?
分析:
结束
输出i
开始
S≤2010
Y
N
i ← 0
S ← 0
i ← i + 1
S ← S + i
S>2010
结束
输出i
开始
Y
N
i ← 0
S ← 0
i ← i + 1
S ← S + i
1+2+3+…+n>2010
例3:请设计一个算法计算满足下列不等式的最小正数n.
直到型循环与当型循环通常可以互
相转化.需注意在将当型循环改写为
直到型循环时,循环体不变,但位置
要放到条件之前,循环条件变为原来
的相反条件;而直到型循环改写为当
型循环时,过程相反.
1.程序框图输出的结果为 ________.
输出a
开始
结束
a=2,i=1
a=2×a
i=i+1
i>5
否
是
练 习
2.如图,根据条件填空,
把程序框图补充完整,
求1~2008所有偶数之和,
则应填:
(1) ,(2) .
图(5)
输出s
开始
结束
i=0,s=0
(1)
(2)
i≤2008
是
否
练 习
3.如图给出的是
计算
的值的一个程序框图,其中判断框内应填入的条件是( )
A.
B.
C.
D.
4.如图所示的程序框图中,语句“输出i”被执行的次数为 ( )
A.32 B.33
C.34 D.35
5.如果右边程序框图
的输出结果为 -18,
那么在判断框中①表示
的“条件”应该是( )
A.
B.
C.
D.
7.设计一个算法求
的和,并画出程序框图.
二.算法建模
1.给出10个数,要求把大于或等于40的数找出并输出,设计算法并画出流程图。
解:算法步骤:
令i=1;
输入数x;
判断x≥40是否成立?若是,则输出x;
否则执行第4步;
令i=i+1;
判断i>10是否成立,若是,则结束,否则返回第2步
变式:求大于或等于40的数的平均数.
2.利用二分法求方程 的近似解的算法流程图.
例2 请根据要求,将右图中的流程图填写完整.
编制计算y=x2的流程图,其中x=-10,-9,-8,
…,0,1,…,9,10.
x ← -10
①
N
输出x,y
结束
Y
开始
y← x2
②
x ← -10
x>10
Y
输出x,y
结束
N
开始
y← x2
x ← x+1
x≤10
x ← x+1
练习2:下面表示了一个什么样的算法? 代表第个学生的学号, 代表第个学生的成绩.
流程图表示将50个学生中成绩不低于80分的学生的学号和成绩打印出来.
拓展提高
任意给定一个大于1的正整数n,设计一个算法对n是否为质数作出判断,并画出流程图。
根据质数的定义用逐一检查法,即逐步检查2~(n-1)中是否存在整除n的数,算法如下:
S1 输入n;
S2 判断n=2是否成立.若“n=2”为真,则输出“n为质数”;
否则,转S3;
S3 i←2;
S4 判断i能整除n吗 若“i 整除n”为真,则输出“n不是质数”;
否则,i←i+1;
S5 判断i >n-1成立吗 若“i >n-1”为真,则输出“n为质数”;
否则,转S4;
开始
输出n不是质数
n =2
i ←2
i 整除n
i←i +1
i ≥n
输出n是质数
输入n
结束
Y
Y
Y
N
N
N
直到型循环
开始
n =2
i ←2
i 不整除n
i←i +1
i < n
输出n是质数
输入n
结束
Y
Y
N
N
Y
N
输出n是质数
输出n不是质数
当型循环
作业:
1.教案;
2.订正加复习.
流程图(3)----循环结构
开始
输入a,b,c
a>b且a>c
b>c
Y
N
Y
N
输出a
输出c
输出b
结束
右面的流程图表示了一个什么样的算法?如果要实现
上述流程图所表示的目的,是否还有其它的算法?
结束
输出S
S ←
开始
S← S +i
i ← i +
Y
N
i ←
0
开始
S ←
结束
输出S
i←
S←S+i
i←i+
N
Y
当型 后计数
直到型 后计数
0
1
2
2
1
i≤99
i=101
i≥101
i>99
流程图欣赏:
结束
输出S
S ←
开始
i ← i +
S ← S +i
Y
N
i ←
开始
S ←
结束
输出S
i←
i←i+
S←S+i
N
Y
直到型 先计数
当型 先计数
1
1
2
2
1
1
i=99
i≤97
i≥99
i>97
流程图欣赏:
1.算法的基本逻辑结构有三种,即顺序结构、条件结构和循环结构。
其中顺序结构是最简单的结构,也是最基本的结构,循环结构必然包含条件结构,所以这三种基本逻辑结构是相互支撑的,无论怎样复杂的逻辑结构,都可以通过这三种结构来表达 。
3.在循环结构中都有一个计数变量和累加变量。计数变量用于记录循环次数,累加变量用于输出结果。计数变量和累加变量一般是同步执行的,累加一次,计数一次。
2.循环结构要在某个条件下终止循环,这就需要条件结构来判断。因此,循环结构中一定包含条件结构,但不允许“死循环”。
循环结构的三要素
循环变量,循环体、循环的终止条件。
4.画循环结构流程图前:
①确定循环变量和初始条件;
②确定算法中反复执行的部分,即循环体;
③确定循环的转向位置;
④确定循环的终止条件.
【课堂互动●例题】
解:算法如下: S1 输入a,b; S2 r←mod(a,b); q←(a r)/b; S3 输出q,r; S4 结束.
例1.写出求两个正整数a与b相除所得的商q及余数r的一个算法,并画出流程图.(提示:用mod(a,b)表示a除以b所得的余数)
流程框图为
r←mod(a,b)
q←(a r)/b
输出q,r
输入a,b
开始
结束
【课堂互动●例题】
解:算法如下: S1 输入票价x; S2 如果x<2那么y=0,否则如果 那么y=x 2 否则y=x 2( +1), S3 输出返还金额y; S4 结束.
流程框图为
例2.火车站对乘客在一定时段内退票要收取一定的费用,收费的办法是:按票价每10元(不足10元按10元计算)核收2元,票价在2元以下的不退.试分步写出将票价为x元的车票退掉后,返还的金额y元的算法,并画出流程图.
Y
N
y←0
输出y
输入票价x
x<2
y←x 2
y←x 2( +1)
Y
N
开始
结束
例3.写出在数3,5,8,9,12,15,35,7,18,52中搜索数18的一个算法,并画出流程图.
【课堂互动●例题】
开始
输入n
n=18
N
输出n
结束
Y
解:算法如下: S1 输入n; S2 如果n=18,则转S3, 否则转S1 S3 输出n; S4 结束.
例4.写出求
(共有6个2)的值的一个算法,并画出流程图.
开始
I←1
I≥6
Y
输出S
结束
S←1/2
I←I+1
S←1/(2+S)
N
解:算法如下: S1 S← ; S2 I←1; S3 S← ,I←I+1; S4 如果I 小于6,那么转S3 S5 输出S; S6 结束.
解:S1 T←0;
S2 I←1;
S5 I←I+1,转S3;
S3 如果I≤100,那么转S4,
否则转S6;
S4 T←T+1/I;
S6 输出T.
【学生活动】
设计计算 ,的一个算法, 并画出流程图 .
开始
I≤100
Y
N
结束
T←1
I←I+1
输出T
I←1
T←T+1/I
开始
I≤100
Y
N
结束
T←1
I←I+1
输出T
I←1
T←T+1/I
【学生练习】请说出下列程序框图表示的算法功能:
T≥10000
Y
N
T←1
I←I+3
输出I
I←3
T←T×I
开始
结束
1+2+3+…+n>2010.
3.退出循环的条件是什么?
1.你准备用哪种循环
例3:请设计一个算法计算满足下列不等式的最小正数n.
2.你认为如何设计累加变量和计数器的初始值比较合适?
分析:
结束
输出i
开始
S≤2010
Y
N
i ← 0
S ← 0
i ← i + 1
S ← S + i
S>2010
结束
输出i
开始
Y
N
i ← 0
S ← 0
i ← i + 1
S ← S + i
1+2+3+…+n>2010
例3:请设计一个算法计算满足下列不等式的最小正数n.
直到型循环与当型循环通常可以互
相转化.需注意在将当型循环改写为
直到型循环时,循环体不变,但位置
要放到条件之前,循环条件变为原来
的相反条件;而直到型循环改写为当
型循环时,过程相反.
1.程序框图输出的结果为 ________.
输出a
开始
结束
a=2,i=1
a=2×a
i=i+1
i>5
否
是
练 习
2.如图,根据条件填空,
把程序框图补充完整,
求1~2008所有偶数之和,
则应填:
(1) ,(2) .
图(5)
输出s
开始
结束
i=0,s=0
(1)
(2)
i≤2008
是
否
练 习
3.如图给出的是
计算
的值的一个程序框图,其中判断框内应填入的条件是( )
A.
B.
C.
D.
4.如图所示的程序框图中,语句“输出i”被执行的次数为 ( )
A.32 B.33
C.34 D.35
5.如果右边程序框图
的输出结果为 -18,
那么在判断框中①表示
的“条件”应该是( )
A.
B.
C.
D.
7.设计一个算法求
的和,并画出程序框图.
二.算法建模
1.给出10个数,要求把大于或等于40的数找出并输出,设计算法并画出流程图。
解:算法步骤:
令i=1;
输入数x;
判断x≥40是否成立?若是,则输出x;
否则执行第4步;
令i=i+1;
判断i>10是否成立,若是,则结束,否则返回第2步
变式:求大于或等于40的数的平均数.
2.利用二分法求方程 的近似解的算法流程图.
例2 请根据要求,将右图中的流程图填写完整.
编制计算y=x2的流程图,其中x=-10,-9,-8,
…,0,1,…,9,10.
x ← -10
①
N
输出x,y
结束
Y
开始
y← x2
②
x ← -10
x>10
Y
输出x,y
结束
N
开始
y← x2
x ← x+1
x≤10
x ← x+1
练习2:下面表示了一个什么样的算法? 代表第个学生的学号, 代表第个学生的成绩.
流程图表示将50个学生中成绩不低于80分的学生的学号和成绩打印出来.
拓展提高
任意给定一个大于1的正整数n,设计一个算法对n是否为质数作出判断,并画出流程图。
根据质数的定义用逐一检查法,即逐步检查2~(n-1)中是否存在整除n的数,算法如下:
S1 输入n;
S2 判断n=2是否成立.若“n=2”为真,则输出“n为质数”;
否则,转S3;
S3 i←2;
S4 判断i能整除n吗 若“i 整除n”为真,则输出“n不是质数”;
否则,i←i+1;
S5 判断i >n-1成立吗 若“i >n-1”为真,则输出“n为质数”;
否则,转S4;
开始
输出n不是质数
n =2
i ←2
i 整除n
i←i +1
i ≥n
输出n是质数
输入n
结束
Y
Y
Y
N
N
N
直到型循环
开始
n =2
i ←2
i 不整除n
i←i +1
i < n
输出n是质数
输入n
结束
Y
Y
N
N
Y
N
输出n是质数
输出n不是质数
当型循环
作业:
1.教案;
2.订正加复习.
