2020-2021学年上海市徐汇区位育中学高三(下)月考数学试卷(2021.03)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市徐汇区位育中学高三(下)月考数学试卷(2021.03)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览




文档简介
2020-2021学年上海市徐汇区位育中学高三(下)月考数学试卷(3月份)
一、填空题(共12小题).
1.抛物线x2=12y的准线方程为 .
2.若函数f(x)=是奇函数,则实数m=
3.若函数f(x)=的反函数为g(x),则函数g(x)的零点为 .
4.在锐角三角形△ABC中,角A、B、C的对边分别为a、b、c,若(b2+c2﹣a2)tanA=bc,则角A的大小为 .
5.若(x3﹣)n的展开式中含有非零常数项,则正整数n的最小值为 .
6.某单位有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,单位均可获赔(每辆车最多只获一次赔偿),设这两辆车在一年内发生此种事故的概率分别为和,且各车是否发生事故相互独立,则一年内该单位在此种保险中获赔的概率为 (结果用最简分数表示)
7.已知等比数列{an}的首项为a1,公比为q,且有,则首项a1的取值范围 .
8.若球的表面积为100π,平面α与球心的距离为3,则平面α截球所得的圆面面积为
9.2018年上海春季高考有23所高校招生,如果某3位同学恰好被其中2所高校录取,那么不同的录取方法有 种.
10.设θ∈[0,2π),若圆(x﹣cosθ)2+(y﹣sinθ)2=r2(r>0)与直线2x﹣y﹣10=0有交点,则r的最小值为
11.已知复数集合A={x+yi||x|≤1,|y|≤1,x,y∈R},,其中i为虚数单位,若复数z∈A∩B,则z对应的点Z在复平面内所形成图形的面积为 .
12.已知正方形ABCD边长为8,,若在正方形边上恰有6个不同的点P,使,则λ的取值范围为 .
二、选择题(共4小题).
13.下列函数是奇函数的是( )
A.f(x)=x+1 B.f(x)=sinx?cosx
C.f(x)=arccosx D.f(x)=
14.若已知极限,则的值为( )
A.﹣3 B. C.﹣1 D.
15.如图是一个正方体的平面展开图,则在该正方体中下列判断错误的是( )
A.BG⊥DE B.CH∥BE C.DG⊥BH D.AE∥CD
16.设向量,其中a2+b2=c2+d2=1,则下列判断错误的是( )
A.向量与z轴正方向的夹角为定值(与c,d之值无关)
B.的最大值为
C.与的夹角的最大值为
D.ad+bc的最大值为1
三、解答题
17.如图,直三棱柱的底面是等腰直角三角形,AB=AC=1,,高等于3,点M1、M2、N1、N2为所在线段的三等分点.
(1)求此三棱柱的体积和三棱锥A1﹣AM1N2的体积;
(2)求异面直线A1N2、AM1所成的角的大小.
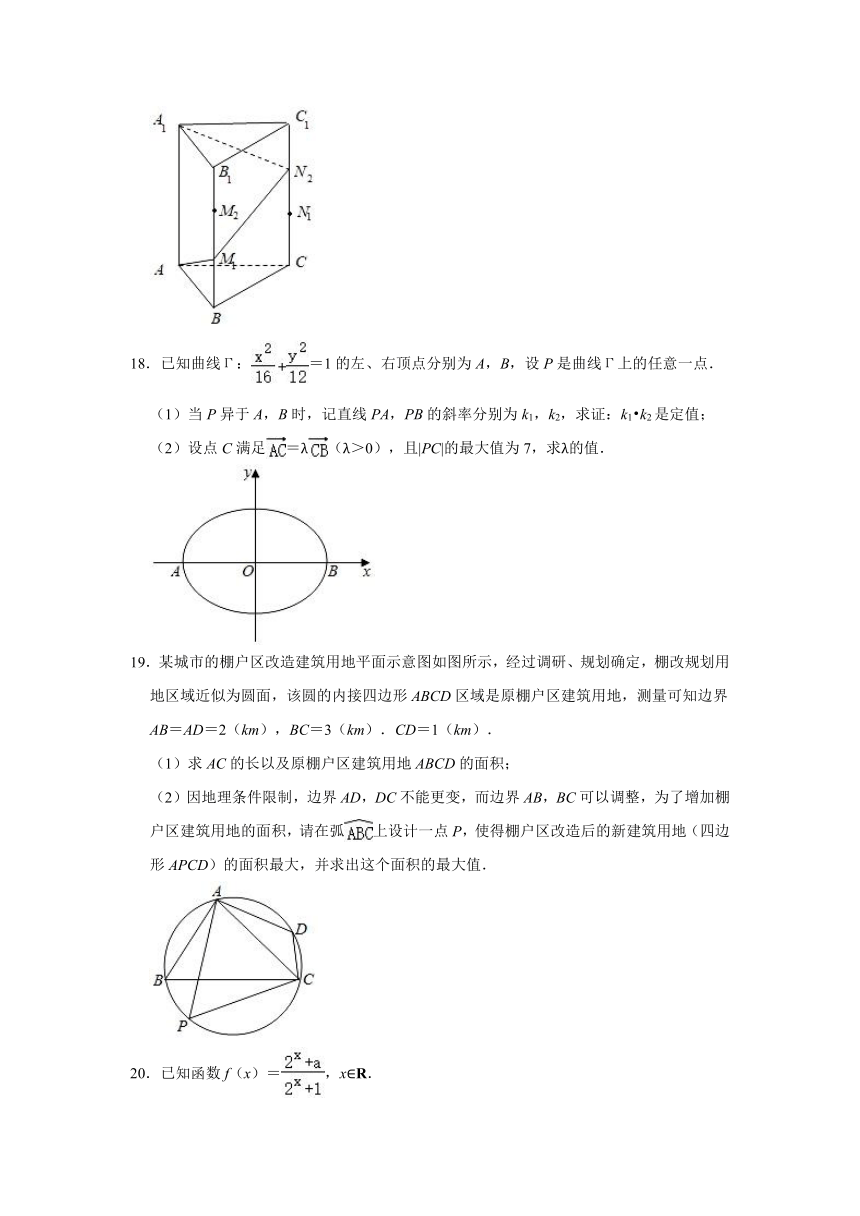
18.已知曲线Γ:=1的左、右顶点分别为A,B,设P是曲线Γ上的任意一点.
(1)当P异于A,B时,记直线PA,PB的斜率分别为k1,k2,求证:k1?k2是定值;
(2)设点C满足=λ(λ>0),且|PC|的最大值为7,求λ的值.
19.某城市的棚户区改造建筑用地平面示意图如图所示,经过调研、规划确定,棚改规划用地区域近似为圆面,该圆的内接四边形ABCD区域是原棚户区建筑用地,测量可知边界AB=AD=2(km),BC=3(km).CD=1(km).
(1)求AC的长以及原棚户区建筑用地ABCD的面积;
(2)因地理条件限制,边界AD,DC不能更变,而边界AB,BC可以调整,为了增加棚户区建筑用地的面积,请在弧上设计一点P,使得棚户区改造后的新建筑用地(四边形APCD)的面积最大,并求出这个面积的最大值.
20.已知函数f(x)=,x∈R.
(1)证明:当a>1时,函数y=f(x)是减函数;
(2)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由;
(3)当a=2,且b<c时,证明:对任意d∈[f(c),f(b)],存在唯一的x0∈R,使得f(x0)=d,且x0∈[b,c].
21.设数列{an}(n∈N*)中前两项a1,a2给定,若对于每个正整数n≥3,均存在正整数k(1≤k≤n﹣1)使得an=,则称数列{an}为“Ω数列”.
(1)若数列{an}(n∈N*)为a1=1,a2=﹣的等比数列,当n≥3时,试问:an与是否相等,并说明数列{an}(n∈N*)是否为“Ω数列”;
(2)讨论首项为a1、公差为d的等差数列{an}是否为“Ω数列”,并说明理由;
(3)已知数列{an}为“Ω数列”,且a1=0,a2=1,记S(n,k)=an﹣1+an﹣2+…+an﹣k,(n≥2,n∈N*),其中正整数k≤n﹣1,对于每个正整数n≥3,当正整数k分别取1、2、…、n﹣1时的最大值记为Mn、最小值记为mn.设bn=n?(Mn﹣mn),当正整数n满足3≤n≤2020时,比较bn与bn+1的大小,并求出bn的最大值.
参考答案
一、填空题(共12小题).
1.抛物线x2=12y的准线方程为 y=﹣3 .
解:抛物线x2=12y的准线方程为:y=﹣3.
故答案为:y=﹣3.
2.若函数f(x)=是奇函数,则实数m=
解:f(x)是奇函数;
∴f(﹣x)=﹣f(x);
即;
∴﹣x﹣2m+1=﹣x+2m﹣1;
∴﹣2m+1=2m﹣1;
∴.
故答案为:.
3.若函数f(x)=的反函数为g(x),则函数g(x)的零点为 .
解:根据题意,函数f(x)=,则f(0)=,
若函数f(x)=的反函数为g(x),则g()=0,
则函数g(x)的零点为;
故答案为:.
4.在锐角三角形△ABC中,角A、B、C的对边分别为a、b、c,若(b2+c2﹣a2)tanA=bc,则角A的大小为 .
解:∵(b2+c2﹣a2)tanA=bc,
∴由余弦定理可得:2bccosA?tanA=bc,可得:sinA=,
∵A为锐角,
∴A=.
故答案为:.
5.若(x3﹣)n的展开式中含有非零常数项,则正整数n的最小值为 5 .
解:(x3﹣)n的展开式的通项为=.
取3n﹣5r=0,得n=,
∴当r=3时,n为最小正整数5.
故答案为:5.
6.某单位有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,单位均可获赔(每辆车最多只获一次赔偿),设这两辆车在一年内发生此种事故的概率分别为和,且各车是否发生事故相互独立,则一年内该单位在此种保险中获赔的概率为 (结果用最简分数表示)
解:某单位有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,
单位均可获赔(每辆车最多只获一次赔偿),
设这两辆车在一年内发生此种事故的概率分别为和,且各车是否发生事故相互独立,
则一年内该单位在此种保险中获赔的概率为p=1﹣=.
故答案为:.
7.已知等比数列{an}的首项为a1,公比为q,且有,则首项a1的取值范围 0<a1<1且a1≠或a1=3 .
解:∵,
∴qn一定存在,∴0<|q|<1或q=1.
当q=1时,,∴a1=3.
当0<|q|<1时,由,得
,
∴2a1﹣1=q.
∴0<|2a1﹣1|<1.
∴0<a1<1且a1≠.
综上,得0<a1<1且a1≠或a1=3.
8.若球的表面积为100π,平面α与球心的距离为3,则平面α截球所得的圆面面积为 16π
解:设球的半径为R,球心到平面α的距离为d,平面α截球所得圆面的半径为r,则d=3,
由于球的表面积为100π,即4πR2=100π,则R=5,
由勾股定理可得,
因此,平面α截球所得圆面的面积为πr2=π×42=16π,
故答案为:16π.
9.2018年上海春季高考有23所高校招生,如果某3位同学恰好被其中2所高校录取,那么不同的录取方法有 1518 种.
解:由题意知本题是一个分步计数问题,
解决这个问题得分三步完成,
第一步把三个学生分成两组,
第二步从23所学校中取两个学校,
第三步,把学生分到两个学校中,共有C31C22A232=1518,
故答案为:1518.
10.设θ∈[0,2π),若圆(x﹣cosθ)2+(y﹣sinθ)2=r2(r>0)与直线2x﹣y﹣10=0有交点,则r的最小值为
解:根据题意,圆(x﹣cosθ)2+(y﹣sinθ)2=r2(r>0)的圆心为(cosθ,sinθ),
则圆心到直线2x﹣y﹣10=0的距离d==,
若圆与直线有交点,则d≤r,
又由﹣≤2cosθ﹣sinθ≤,
则2﹣1≤d≤2+1,
则有r≥2﹣1,即r的最小值为2﹣1,
故答案为:2﹣1.
11.已知复数集合A={x+yi||x|≤1,|y|≤1,x,y∈R},,其中i为虚数单位,若复数z∈A∩B,则z对应的点Z在复平面内所形成图形的面积为 .
解:集合A={x+yi||x|≤1,|y|≤1,x,y∈R)在复平面内所形成的图形为正方形ABCD内包括边界,
z2=(1+i)z1=(cos+isin)z1对应的点在复平面内形成的图象为正方形PQRS,如图:
所以所求图形的面积为﹣4×=﹣1=,
故答案为:
12.已知正方形ABCD边长为8,,若在正方形边上恰有6个不同的点P,使,则λ的取值范围为 (﹣1,8) .
解:以AB所在直线为x轴,以AD所在直线为y轴建立平面直角坐标系如图:如图,则F(0,2),E(8,4)
(1)若P在AB上,设P(x,0),0≤x≤8
∴=(﹣x,2),=(8﹣x,4)
∴?=x2﹣8x+8,
∵x∈[0,8],∴﹣8≤?≤8,
∴当λ=﹣8时有一解,当﹣8<λ≤8时有两解;
(2)若P在AD上,设P(0,y),0<y≤8,
∴=(0,2﹣y),=(8,4﹣y)
∴?=(2﹣y)(4﹣y)=y2﹣6y+8
∵0<y≤8,∴﹣1≤?<24
∴当λ=﹣1或8<λ<24时有唯一解;当﹣1<λ≤8时有两解
(3)若P在DC上,设P(x,8),0<x≤8
∴=(﹣x,﹣6),=(8﹣x,﹣4),
∴?=x2﹣8x+24,
∵0<x≤8,∴8≤?≤24,
∴当λ=8时有一解,当8<λ≤24时有两解.
(4)若P在BC上,设P(8,y),0<y<8,
∴=(﹣8,2﹣y),=(0,4﹣y),
∴?=(2﹣y)?(4﹣y)=y2﹣6y+8
∵0<y<8,∴﹣1≤?<24,
∴当λ=﹣1或8<λ<24时有一解,当﹣1<λ≤8时有两解.
综上,在正方形ABCD的四条边上有且只有6个不同的点P,使得?=λ成立,那么λ的取值范围是(﹣1,8)
故答案为:(﹣1,8)
二、选择题
13.下列函数是奇函数的是( )
A.f(x)=x+1 B.f(x)=sinx?cosx
C.f(x)=arccosx D.f(x)=
解:根据题意,依次分析选项:
对于A,f(x)=x+1,则f(﹣x)=﹣x+1,则f(﹣x)≠﹣f(x)且f(﹣x)≠f(x),则函数f(x)既不是奇函数又不是偶函数,不符合题意;
对于B,f(x)=sinxcosx,则f(﹣x)=sin(﹣x)cos(﹣x)=﹣sinxcosx=﹣f(x),函数f(x)为奇函数,符合题意;
对于C,f(x)=arccosx,为反三角函数,则函数f(x)既不是奇函数又不是偶函数,不符合题意;
对于D,f(x)=,有f(﹣x)=f(x),函数f(x)为偶函数,不符合题意;
故选:B.
14.若已知极限,则的值为( )
A.﹣3 B. C.﹣1 D.
解:∵;
∴=.
故选:D.
15.如图是一个正方体的平面展开图,则在该正方体中下列判断错误的是( )
A.BG⊥DE B.CH∥BE C.DG⊥BH D.AE∥CD
解:还原原正方体如图,
连接CF,可得DE∥CF,又CF⊥BG,∴BG⊥DE,故A正确;
由图可知,CH∥BE,故B正确;
∵DG⊥CH,CH为BH在平面DCGH上的射影,∴DG⊥BH,故C正确;
AE与CD是异面直线,故D错误.
故选:D.
16.设向量,其中a2+b2=c2+d2=1,则下列判断错误的是( )
A.向量与z轴正方向的夹角为定值(与c,d之值无关)
B.的最大值为
C.与的夹角的最大值为
D.ad+bc的最大值为1
解:由向量,其中a2+b2=c2+d2=1,知:
在A中,设z轴正方向的方向向量=(0,0,t),
向量与z轴正方向的夹角的余弦值:
cosα===,∴α=45°,
∴向量与z轴正方向的夹角为定值45°(与c,d之值无关),故A正确;
在B中,=ac+bd≤==1,
且仅当a=c,b=d时取等号,因此的最大值为1,故B错误;
在C中,由B可得:||≤1,∴﹣1≤≤1,
∴cos<>==≥﹣=﹣,
∴与的夹角的最大值为,故C正确;
在D中,ad+bc≤+==1,
∴ad+bc的最大值为1.故D正确.
故选:B.
三、解答题
17.如图,直三棱柱的底面是等腰直角三角形,AB=AC=1,,高等于3,点M1、M2、N1、N2为所在线段的三等分点.
(1)求此三棱柱的体积和三棱锥A1﹣AM1N2的体积;
(2)求异面直线A1N2、AM1所成的角的大小.
解:(1)∵直三棱柱的底面是等腰直角三角形,
AB=AC=1,,高等于3,
∴此三棱柱的体积V=S△BAC×AA1==.
∵点M1、M2、N1、N2为所在线段的三等分点.
M1到平面AA1N2的距离d=AB=1,
∴三棱锥A1﹣AM1N2的体积:
==×d
==.
(2)以A为原点,AB为x轴,AC为y轴,AA1为z轴,
建立空间直角坐标系,
A1(0,0,3),N2(0,1,2),A(0,0,0),M1(1,0,1),
=(0,1,﹣1),=(1,0,1),
设异面直线A1N2、AM1所成的角为θ,
则cosθ===,∴θ=,
∴异面直线A1N2、AM1所成的角为.
18.已知曲线Γ:=1的左、右顶点分别为A,B,设P是曲线Γ上的任意一点.
(1)当P异于A,B时,记直线PA,PB的斜率分别为k1,k2,求证:k1?k2是定值;
(2)设点C满足=λ(λ>0),且|PC|的最大值为7,求λ的值.
【解答】(1)证明:由椭圆方程可得A(﹣4,0),B(4,0),
设P(x0,y0)(﹣4≤x0≤4),
则,,
∴k1?k2==为定值;
(2)解:设C(m,0)(﹣4<m<4),
则=
=.
若m≥0,则=7,解得m=3.
此时,,,
由=λ,得λ=7;
同理,若m<0,可得m=﹣3,此时求得.
故λ的值为7或.
19.某城市的棚户区改造建筑用地平面示意图如图所示,经过调研、规划确定,棚改规划用地区域近似为圆面,该圆的内接四边形ABCD区域是原棚户区建筑用地,测量可知边界AB=AD=2(km),BC=3(km).CD=1(km).
(1)求AC的长以及原棚户区建筑用地ABCD的面积;
(2)因地理条件限制,边界AD,DC不能更变,而边界AB,BC可以调整,为了增加棚户区建筑用地的面积,请在弧上设计一点P,使得棚户区改造后的新建筑用地(四边形APCD)的面积最大,并求出这个面积的最大值.
解:(1)四边形ABCD中,B+D=π,
∴cosB+cosD=0,
即+=0,
解得AC=,
且cosB=﹣cosD=;
∴sinB=sinD=,
∴建筑用地ABCD的面积为
S=×(2×1+2×3)×sinB=2;
(2)设CP=x,AP=y,
由余弦定理得x2+y2﹣xy=7,
又7=x2+y2﹣xy≥2xy﹣xy=xy,当且仅当x=y时,等号成立;
得S四边形APCD=×2×1×+xy?≤,
所以,当且仅当AP=CP,
即P为线段AC垂直平分线与弧交点时,面积最大,
此时△APC为等边三角形,四边形APCD的面积最大,最大值为.
20.已知函数f(x)=,x∈R.
(1)证明:当a>1时,函数y=f(x)是减函数;
(2)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由;
(3)当a=2,且b<c时,证明:对任意d∈[f(c),f(b)],存在唯一的x0∈R,使得f(x0)=d,且x0∈[b,c].
【解答】(1)证明:任取x1,x2∈R,设x1<x2,则f(x1)﹣f(x2)=,
∵x1<x2,∴<,又a>1,∴f(x1)﹣f(x2)>0,即f(x1)>f(x2).
所以当a>1时,函数y=f(x)是减函数.
(2)解:当a=1时,f(x)=1,所以f(﹣x)=f(x)=1,所以函数y=f(x)是偶函数,
当a=﹣1时,f(x)=,f(﹣x)===﹣f(x),
所以函数y=f(x)是奇函数.
当a≠1且a≠﹣1时,f(1)=,f(﹣1)=,
∴f(﹣1)≠f(1)且f(﹣1)≠﹣f(1),
所以函数y=f(x)是非奇非偶函数.
(3)证明:由(1)知,当a=2时,函数y=f(x)是减函数,
所以函数f(x)在[b,c]上的值域为[f(c),f(b)],
因为d∈[f(c),f(b)],所以存在x0∈R,使得f(x0)=d.
假设存在x1∈R,x1≠0使得f(x1)=d,
若x1>x0,由f(x)的单调性可得f(x1)<f(x0),若x1<x0,则f(x1)>f(x0),
与f(x1)=f(x0)=d矛盾,故x0是唯一的.
假设x0?[b,c],即x0<b或x0>c,
由单调性可得f(x0)>f(b)或f(x0)<f(c),
所以d?[f(c),f(b)],与d∈[f(c),f(b)]矛盾,故x0∈[b,c].
21.设数列{an}(n∈N*)中前两项a1,a2给定,若对于每个正整数n≥3,均存在正整数k(1≤k≤n﹣1)使得an=,则称数列{an}为“Ω数列”.
(1)若数列{an}(n∈N*)为a1=1,a2=﹣的等比数列,当n≥3时,试问:an与是否相等,并说明数列{an}(n∈N*)是否为“Ω数列”;
(2)讨论首项为a1、公差为d的等差数列{an}是否为“Ω数列”,并说明理由;
(3)已知数列{an}为“Ω数列”,且a1=0,a2=1,记S(n,k)=an﹣1+an﹣2+…+an﹣k,(n≥2,n∈N*),其中正整数k≤n﹣1,对于每个正整数n≥3,当正整数k分别取1、2、…、n﹣1时的最大值记为Mn、最小值记为mn.设bn=n?(Mn﹣mn),当正整数n满足3≤n≤2020时,比较bn与bn+1的大小,并求出bn的最大值.
解:(1)∵数列{an}(n∈N*)为a1=1,a2=﹣的等比数列,∴an=(﹣)n﹣1.
由于当n≥3时,均有==?(﹣)n﹣3=(﹣)n﹣1=an,
∴an与相等.
∵对每个正整数n≥3,均存在正整数k=2且1≤2≤n﹣1,使得an=,
∴数列{an}为“Ω数列“.
(2)d=0时,对于每个正整数n≥3,均存在正整数k=1,
∵1≤1≤n﹣1,使,∴d=0时,数列{an}为Ω数列,
d>0时,,且,
d<0时,.
∴d≠0时,对n=3,当正整数k在1≤k≤3﹣1时,
总有,
∴d≠0时,数列{an}不是Ω数列.
(3)由题设知对于每个正整数n≥3,均有an∈[mn,Mn],∈[mn,Mn],
且对于所有正整数k≤n﹣1,均有mn≤,即kMn≤S(n,k)≤kMn,
记S(n,0)=0,
对于每个正整数n≥4,选取适当的正整数l,l≤n﹣1,使得Mn=,
由S(n,l)=an﹣1+S(n﹣1,l﹣1)≤an﹣1+(l﹣1)Mn﹣1,
则l(Mn﹣an﹣1)=lMn﹣lan﹣1=S(n,l)﹣lan﹣1≤an﹣1+(l﹣1)Mn﹣1﹣lan﹣1=(l﹣1)Mn﹣1﹣an﹣1,
即Mn﹣an﹣1≤,
类似的,
l(an﹣1﹣mn)=lan﹣1﹣lmn=lan﹣1﹣S(n,l)=lan﹣1﹣an﹣1﹣S(n﹣1,l﹣1)
≤(l﹣1)an﹣1﹣(l﹣1)mn﹣1=(l﹣1)(an﹣1﹣mn﹣1),
∵mn﹣1≤an﹣1≤Mn﹣1?t≤n﹣1,l≤n﹣1,
∴Mn﹣mn,
∴Mn﹣mn=(Mn﹣an﹣1)+(an﹣1﹣mn)≤+
==,
∴Mn﹣mn≤,
∵a1=0,a2=1,∴mn﹣1≠Mn﹣1,
∴n(Mn﹣mn)<(n﹣1)(Mn﹣1﹣mn﹣1),
∴正整数n≥4时,bn<bn﹣1成立,
即正整数n>3时,bn+1<bn成立,
∴在正整数n满足3≤n≤2020时,
当n=3时,bn取最大值为b3=3(1﹣)=.
一、填空题(共12小题).
1.抛物线x2=12y的准线方程为 .
2.若函数f(x)=是奇函数,则实数m=
3.若函数f(x)=的反函数为g(x),则函数g(x)的零点为 .
4.在锐角三角形△ABC中,角A、B、C的对边分别为a、b、c,若(b2+c2﹣a2)tanA=bc,则角A的大小为 .
5.若(x3﹣)n的展开式中含有非零常数项,则正整数n的最小值为 .
6.某单位有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,单位均可获赔(每辆车最多只获一次赔偿),设这两辆车在一年内发生此种事故的概率分别为和,且各车是否发生事故相互独立,则一年内该单位在此种保险中获赔的概率为 (结果用最简分数表示)
7.已知等比数列{an}的首项为a1,公比为q,且有,则首项a1的取值范围 .
8.若球的表面积为100π,平面α与球心的距离为3,则平面α截球所得的圆面面积为
9.2018年上海春季高考有23所高校招生,如果某3位同学恰好被其中2所高校录取,那么不同的录取方法有 种.
10.设θ∈[0,2π),若圆(x﹣cosθ)2+(y﹣sinθ)2=r2(r>0)与直线2x﹣y﹣10=0有交点,则r的最小值为
11.已知复数集合A={x+yi||x|≤1,|y|≤1,x,y∈R},,其中i为虚数单位,若复数z∈A∩B,则z对应的点Z在复平面内所形成图形的面积为 .
12.已知正方形ABCD边长为8,,若在正方形边上恰有6个不同的点P,使,则λ的取值范围为 .
二、选择题(共4小题).
13.下列函数是奇函数的是( )
A.f(x)=x+1 B.f(x)=sinx?cosx
C.f(x)=arccosx D.f(x)=
14.若已知极限,则的值为( )
A.﹣3 B. C.﹣1 D.
15.如图是一个正方体的平面展开图,则在该正方体中下列判断错误的是( )
A.BG⊥DE B.CH∥BE C.DG⊥BH D.AE∥CD
16.设向量,其中a2+b2=c2+d2=1,则下列判断错误的是( )
A.向量与z轴正方向的夹角为定值(与c,d之值无关)
B.的最大值为
C.与的夹角的最大值为
D.ad+bc的最大值为1
三、解答题
17.如图,直三棱柱的底面是等腰直角三角形,AB=AC=1,,高等于3,点M1、M2、N1、N2为所在线段的三等分点.
(1)求此三棱柱的体积和三棱锥A1﹣AM1N2的体积;
(2)求异面直线A1N2、AM1所成的角的大小.
18.已知曲线Γ:=1的左、右顶点分别为A,B,设P是曲线Γ上的任意一点.
(1)当P异于A,B时,记直线PA,PB的斜率分别为k1,k2,求证:k1?k2是定值;
(2)设点C满足=λ(λ>0),且|PC|的最大值为7,求λ的值.
19.某城市的棚户区改造建筑用地平面示意图如图所示,经过调研、规划确定,棚改规划用地区域近似为圆面,该圆的内接四边形ABCD区域是原棚户区建筑用地,测量可知边界AB=AD=2(km),BC=3(km).CD=1(km).
(1)求AC的长以及原棚户区建筑用地ABCD的面积;
(2)因地理条件限制,边界AD,DC不能更变,而边界AB,BC可以调整,为了增加棚户区建筑用地的面积,请在弧上设计一点P,使得棚户区改造后的新建筑用地(四边形APCD)的面积最大,并求出这个面积的最大值.
20.已知函数f(x)=,x∈R.
(1)证明:当a>1时,函数y=f(x)是减函数;
(2)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由;
(3)当a=2,且b<c时,证明:对任意d∈[f(c),f(b)],存在唯一的x0∈R,使得f(x0)=d,且x0∈[b,c].
21.设数列{an}(n∈N*)中前两项a1,a2给定,若对于每个正整数n≥3,均存在正整数k(1≤k≤n﹣1)使得an=,则称数列{an}为“Ω数列”.
(1)若数列{an}(n∈N*)为a1=1,a2=﹣的等比数列,当n≥3时,试问:an与是否相等,并说明数列{an}(n∈N*)是否为“Ω数列”;
(2)讨论首项为a1、公差为d的等差数列{an}是否为“Ω数列”,并说明理由;
(3)已知数列{an}为“Ω数列”,且a1=0,a2=1,记S(n,k)=an﹣1+an﹣2+…+an﹣k,(n≥2,n∈N*),其中正整数k≤n﹣1,对于每个正整数n≥3,当正整数k分别取1、2、…、n﹣1时的最大值记为Mn、最小值记为mn.设bn=n?(Mn﹣mn),当正整数n满足3≤n≤2020时,比较bn与bn+1的大小,并求出bn的最大值.
参考答案
一、填空题(共12小题).
1.抛物线x2=12y的准线方程为 y=﹣3 .
解:抛物线x2=12y的准线方程为:y=﹣3.
故答案为:y=﹣3.
2.若函数f(x)=是奇函数,则实数m=
解:f(x)是奇函数;
∴f(﹣x)=﹣f(x);
即;
∴﹣x﹣2m+1=﹣x+2m﹣1;
∴﹣2m+1=2m﹣1;
∴.
故答案为:.
3.若函数f(x)=的反函数为g(x),则函数g(x)的零点为 .
解:根据题意,函数f(x)=,则f(0)=,
若函数f(x)=的反函数为g(x),则g()=0,
则函数g(x)的零点为;
故答案为:.
4.在锐角三角形△ABC中,角A、B、C的对边分别为a、b、c,若(b2+c2﹣a2)tanA=bc,则角A的大小为 .
解:∵(b2+c2﹣a2)tanA=bc,
∴由余弦定理可得:2bccosA?tanA=bc,可得:sinA=,
∵A为锐角,
∴A=.
故答案为:.
5.若(x3﹣)n的展开式中含有非零常数项,则正整数n的最小值为 5 .
解:(x3﹣)n的展开式的通项为=.
取3n﹣5r=0,得n=,
∴当r=3时,n为最小正整数5.
故答案为:5.
6.某单位有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,单位均可获赔(每辆车最多只获一次赔偿),设这两辆车在一年内发生此种事故的概率分别为和,且各车是否发生事故相互独立,则一年内该单位在此种保险中获赔的概率为 (结果用最简分数表示)
解:某单位有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,
单位均可获赔(每辆车最多只获一次赔偿),
设这两辆车在一年内发生此种事故的概率分别为和,且各车是否发生事故相互独立,
则一年内该单位在此种保险中获赔的概率为p=1﹣=.
故答案为:.
7.已知等比数列{an}的首项为a1,公比为q,且有,则首项a1的取值范围 0<a1<1且a1≠或a1=3 .
解:∵,
∴qn一定存在,∴0<|q|<1或q=1.
当q=1时,,∴a1=3.
当0<|q|<1时,由,得
,
∴2a1﹣1=q.
∴0<|2a1﹣1|<1.
∴0<a1<1且a1≠.
综上,得0<a1<1且a1≠或a1=3.
8.若球的表面积为100π,平面α与球心的距离为3,则平面α截球所得的圆面面积为 16π
解:设球的半径为R,球心到平面α的距离为d,平面α截球所得圆面的半径为r,则d=3,
由于球的表面积为100π,即4πR2=100π,则R=5,
由勾股定理可得,
因此,平面α截球所得圆面的面积为πr2=π×42=16π,
故答案为:16π.
9.2018年上海春季高考有23所高校招生,如果某3位同学恰好被其中2所高校录取,那么不同的录取方法有 1518 种.
解:由题意知本题是一个分步计数问题,
解决这个问题得分三步完成,
第一步把三个学生分成两组,
第二步从23所学校中取两个学校,
第三步,把学生分到两个学校中,共有C31C22A232=1518,
故答案为:1518.
10.设θ∈[0,2π),若圆(x﹣cosθ)2+(y﹣sinθ)2=r2(r>0)与直线2x﹣y﹣10=0有交点,则r的最小值为
解:根据题意,圆(x﹣cosθ)2+(y﹣sinθ)2=r2(r>0)的圆心为(cosθ,sinθ),
则圆心到直线2x﹣y﹣10=0的距离d==,
若圆与直线有交点,则d≤r,
又由﹣≤2cosθ﹣sinθ≤,
则2﹣1≤d≤2+1,
则有r≥2﹣1,即r的最小值为2﹣1,
故答案为:2﹣1.
11.已知复数集合A={x+yi||x|≤1,|y|≤1,x,y∈R},,其中i为虚数单位,若复数z∈A∩B,则z对应的点Z在复平面内所形成图形的面积为 .
解:集合A={x+yi||x|≤1,|y|≤1,x,y∈R)在复平面内所形成的图形为正方形ABCD内包括边界,
z2=(1+i)z1=(cos+isin)z1对应的点在复平面内形成的图象为正方形PQRS,如图:
所以所求图形的面积为﹣4×=﹣1=,
故答案为:
12.已知正方形ABCD边长为8,,若在正方形边上恰有6个不同的点P,使,则λ的取值范围为 (﹣1,8) .
解:以AB所在直线为x轴,以AD所在直线为y轴建立平面直角坐标系如图:如图,则F(0,2),E(8,4)
(1)若P在AB上,设P(x,0),0≤x≤8
∴=(﹣x,2),=(8﹣x,4)
∴?=x2﹣8x+8,
∵x∈[0,8],∴﹣8≤?≤8,
∴当λ=﹣8时有一解,当﹣8<λ≤8时有两解;
(2)若P在AD上,设P(0,y),0<y≤8,
∴=(0,2﹣y),=(8,4﹣y)
∴?=(2﹣y)(4﹣y)=y2﹣6y+8
∵0<y≤8,∴﹣1≤?<24
∴当λ=﹣1或8<λ<24时有唯一解;当﹣1<λ≤8时有两解
(3)若P在DC上,设P(x,8),0<x≤8
∴=(﹣x,﹣6),=(8﹣x,﹣4),
∴?=x2﹣8x+24,
∵0<x≤8,∴8≤?≤24,
∴当λ=8时有一解,当8<λ≤24时有两解.
(4)若P在BC上,设P(8,y),0<y<8,
∴=(﹣8,2﹣y),=(0,4﹣y),
∴?=(2﹣y)?(4﹣y)=y2﹣6y+8
∵0<y<8,∴﹣1≤?<24,
∴当λ=﹣1或8<λ<24时有一解,当﹣1<λ≤8时有两解.
综上,在正方形ABCD的四条边上有且只有6个不同的点P,使得?=λ成立,那么λ的取值范围是(﹣1,8)
故答案为:(﹣1,8)
二、选择题
13.下列函数是奇函数的是( )
A.f(x)=x+1 B.f(x)=sinx?cosx
C.f(x)=arccosx D.f(x)=
解:根据题意,依次分析选项:
对于A,f(x)=x+1,则f(﹣x)=﹣x+1,则f(﹣x)≠﹣f(x)且f(﹣x)≠f(x),则函数f(x)既不是奇函数又不是偶函数,不符合题意;
对于B,f(x)=sinxcosx,则f(﹣x)=sin(﹣x)cos(﹣x)=﹣sinxcosx=﹣f(x),函数f(x)为奇函数,符合题意;
对于C,f(x)=arccosx,为反三角函数,则函数f(x)既不是奇函数又不是偶函数,不符合题意;
对于D,f(x)=,有f(﹣x)=f(x),函数f(x)为偶函数,不符合题意;
故选:B.
14.若已知极限,则的值为( )
A.﹣3 B. C.﹣1 D.
解:∵;
∴=.
故选:D.
15.如图是一个正方体的平面展开图,则在该正方体中下列判断错误的是( )
A.BG⊥DE B.CH∥BE C.DG⊥BH D.AE∥CD
解:还原原正方体如图,
连接CF,可得DE∥CF,又CF⊥BG,∴BG⊥DE,故A正确;
由图可知,CH∥BE,故B正确;
∵DG⊥CH,CH为BH在平面DCGH上的射影,∴DG⊥BH,故C正确;
AE与CD是异面直线,故D错误.
故选:D.
16.设向量,其中a2+b2=c2+d2=1,则下列判断错误的是( )
A.向量与z轴正方向的夹角为定值(与c,d之值无关)
B.的最大值为
C.与的夹角的最大值为
D.ad+bc的最大值为1
解:由向量,其中a2+b2=c2+d2=1,知:
在A中,设z轴正方向的方向向量=(0,0,t),
向量与z轴正方向的夹角的余弦值:
cosα===,∴α=45°,
∴向量与z轴正方向的夹角为定值45°(与c,d之值无关),故A正确;
在B中,=ac+bd≤==1,
且仅当a=c,b=d时取等号,因此的最大值为1,故B错误;
在C中,由B可得:||≤1,∴﹣1≤≤1,
∴cos<>==≥﹣=﹣,
∴与的夹角的最大值为,故C正确;
在D中,ad+bc≤+==1,
∴ad+bc的最大值为1.故D正确.
故选:B.
三、解答题
17.如图,直三棱柱的底面是等腰直角三角形,AB=AC=1,,高等于3,点M1、M2、N1、N2为所在线段的三等分点.
(1)求此三棱柱的体积和三棱锥A1﹣AM1N2的体积;
(2)求异面直线A1N2、AM1所成的角的大小.
解:(1)∵直三棱柱的底面是等腰直角三角形,
AB=AC=1,,高等于3,
∴此三棱柱的体积V=S△BAC×AA1==.
∵点M1、M2、N1、N2为所在线段的三等分点.
M1到平面AA1N2的距离d=AB=1,
∴三棱锥A1﹣AM1N2的体积:
==×d
==.
(2)以A为原点,AB为x轴,AC为y轴,AA1为z轴,
建立空间直角坐标系,
A1(0,0,3),N2(0,1,2),A(0,0,0),M1(1,0,1),
=(0,1,﹣1),=(1,0,1),
设异面直线A1N2、AM1所成的角为θ,
则cosθ===,∴θ=,
∴异面直线A1N2、AM1所成的角为.
18.已知曲线Γ:=1的左、右顶点分别为A,B,设P是曲线Γ上的任意一点.
(1)当P异于A,B时,记直线PA,PB的斜率分别为k1,k2,求证:k1?k2是定值;
(2)设点C满足=λ(λ>0),且|PC|的最大值为7,求λ的值.
【解答】(1)证明:由椭圆方程可得A(﹣4,0),B(4,0),
设P(x0,y0)(﹣4≤x0≤4),
则,,
∴k1?k2==为定值;
(2)解:设C(m,0)(﹣4<m<4),
则=
=.
若m≥0,则=7,解得m=3.
此时,,,
由=λ,得λ=7;
同理,若m<0,可得m=﹣3,此时求得.
故λ的值为7或.
19.某城市的棚户区改造建筑用地平面示意图如图所示,经过调研、规划确定,棚改规划用地区域近似为圆面,该圆的内接四边形ABCD区域是原棚户区建筑用地,测量可知边界AB=AD=2(km),BC=3(km).CD=1(km).
(1)求AC的长以及原棚户区建筑用地ABCD的面积;
(2)因地理条件限制,边界AD,DC不能更变,而边界AB,BC可以调整,为了增加棚户区建筑用地的面积,请在弧上设计一点P,使得棚户区改造后的新建筑用地(四边形APCD)的面积最大,并求出这个面积的最大值.
解:(1)四边形ABCD中,B+D=π,
∴cosB+cosD=0,
即+=0,
解得AC=,
且cosB=﹣cosD=;
∴sinB=sinD=,
∴建筑用地ABCD的面积为
S=×(2×1+2×3)×sinB=2;
(2)设CP=x,AP=y,
由余弦定理得x2+y2﹣xy=7,
又7=x2+y2﹣xy≥2xy﹣xy=xy,当且仅当x=y时,等号成立;
得S四边形APCD=×2×1×+xy?≤,
所以,当且仅当AP=CP,
即P为线段AC垂直平分线与弧交点时,面积最大,
此时△APC为等边三角形,四边形APCD的面积最大,最大值为.
20.已知函数f(x)=,x∈R.
(1)证明:当a>1时,函数y=f(x)是减函数;
(2)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由;
(3)当a=2,且b<c时,证明:对任意d∈[f(c),f(b)],存在唯一的x0∈R,使得f(x0)=d,且x0∈[b,c].
【解答】(1)证明:任取x1,x2∈R,设x1<x2,则f(x1)﹣f(x2)=,
∵x1<x2,∴<,又a>1,∴f(x1)﹣f(x2)>0,即f(x1)>f(x2).
所以当a>1时,函数y=f(x)是减函数.
(2)解:当a=1时,f(x)=1,所以f(﹣x)=f(x)=1,所以函数y=f(x)是偶函数,
当a=﹣1时,f(x)=,f(﹣x)===﹣f(x),
所以函数y=f(x)是奇函数.
当a≠1且a≠﹣1时,f(1)=,f(﹣1)=,
∴f(﹣1)≠f(1)且f(﹣1)≠﹣f(1),
所以函数y=f(x)是非奇非偶函数.
(3)证明:由(1)知,当a=2时,函数y=f(x)是减函数,
所以函数f(x)在[b,c]上的值域为[f(c),f(b)],
因为d∈[f(c),f(b)],所以存在x0∈R,使得f(x0)=d.
假设存在x1∈R,x1≠0使得f(x1)=d,
若x1>x0,由f(x)的单调性可得f(x1)<f(x0),若x1<x0,则f(x1)>f(x0),
与f(x1)=f(x0)=d矛盾,故x0是唯一的.
假设x0?[b,c],即x0<b或x0>c,
由单调性可得f(x0)>f(b)或f(x0)<f(c),
所以d?[f(c),f(b)],与d∈[f(c),f(b)]矛盾,故x0∈[b,c].
21.设数列{an}(n∈N*)中前两项a1,a2给定,若对于每个正整数n≥3,均存在正整数k(1≤k≤n﹣1)使得an=,则称数列{an}为“Ω数列”.
(1)若数列{an}(n∈N*)为a1=1,a2=﹣的等比数列,当n≥3时,试问:an与是否相等,并说明数列{an}(n∈N*)是否为“Ω数列”;
(2)讨论首项为a1、公差为d的等差数列{an}是否为“Ω数列”,并说明理由;
(3)已知数列{an}为“Ω数列”,且a1=0,a2=1,记S(n,k)=an﹣1+an﹣2+…+an﹣k,(n≥2,n∈N*),其中正整数k≤n﹣1,对于每个正整数n≥3,当正整数k分别取1、2、…、n﹣1时的最大值记为Mn、最小值记为mn.设bn=n?(Mn﹣mn),当正整数n满足3≤n≤2020时,比较bn与bn+1的大小,并求出bn的最大值.
解:(1)∵数列{an}(n∈N*)为a1=1,a2=﹣的等比数列,∴an=(﹣)n﹣1.
由于当n≥3时,均有==?(﹣)n﹣3=(﹣)n﹣1=an,
∴an与相等.
∵对每个正整数n≥3,均存在正整数k=2且1≤2≤n﹣1,使得an=,
∴数列{an}为“Ω数列“.
(2)d=0时,对于每个正整数n≥3,均存在正整数k=1,
∵1≤1≤n﹣1,使,∴d=0时,数列{an}为Ω数列,
d>0时,,且,
d<0时,.
∴d≠0时,对n=3,当正整数k在1≤k≤3﹣1时,
总有,
∴d≠0时,数列{an}不是Ω数列.
(3)由题设知对于每个正整数n≥3,均有an∈[mn,Mn],∈[mn,Mn],
且对于所有正整数k≤n﹣1,均有mn≤,即kMn≤S(n,k)≤kMn,
记S(n,0)=0,
对于每个正整数n≥4,选取适当的正整数l,l≤n﹣1,使得Mn=,
由S(n,l)=an﹣1+S(n﹣1,l﹣1)≤an﹣1+(l﹣1)Mn﹣1,
则l(Mn﹣an﹣1)=lMn﹣lan﹣1=S(n,l)﹣lan﹣1≤an﹣1+(l﹣1)Mn﹣1﹣lan﹣1=(l﹣1)Mn﹣1﹣an﹣1,
即Mn﹣an﹣1≤,
类似的,
l(an﹣1﹣mn)=lan﹣1﹣lmn=lan﹣1﹣S(n,l)=lan﹣1﹣an﹣1﹣S(n﹣1,l﹣1)
≤(l﹣1)an﹣1﹣(l﹣1)mn﹣1=(l﹣1)(an﹣1﹣mn﹣1),
∵mn﹣1≤an﹣1≤Mn﹣1?t≤n﹣1,l≤n﹣1,
∴Mn﹣mn,
∴Mn﹣mn=(Mn﹣an﹣1)+(an﹣1﹣mn)≤+
==,
∴Mn﹣mn≤,
∵a1=0,a2=1,∴mn﹣1≠Mn﹣1,
∴n(Mn﹣mn)<(n﹣1)(Mn﹣1﹣mn﹣1),
∴正整数n≥4时,bn<bn﹣1成立,
即正整数n>3时,bn+1<bn成立,
∴在正整数n满足3≤n≤2020时,
当n=3时,bn取最大值为b3=3(1﹣)=.
同课章节目录
