2020-2021学年七年级数学苏科版下册 第7章 7.2探索平行线的性质 每课1练课时作业(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册 第7章 7.2探索平行线的性质 每课1练课时作业(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 20:20:51 | ||
图片预览


文档简介
课时作业(三)A
[探索平行线的性质]
一、选择题
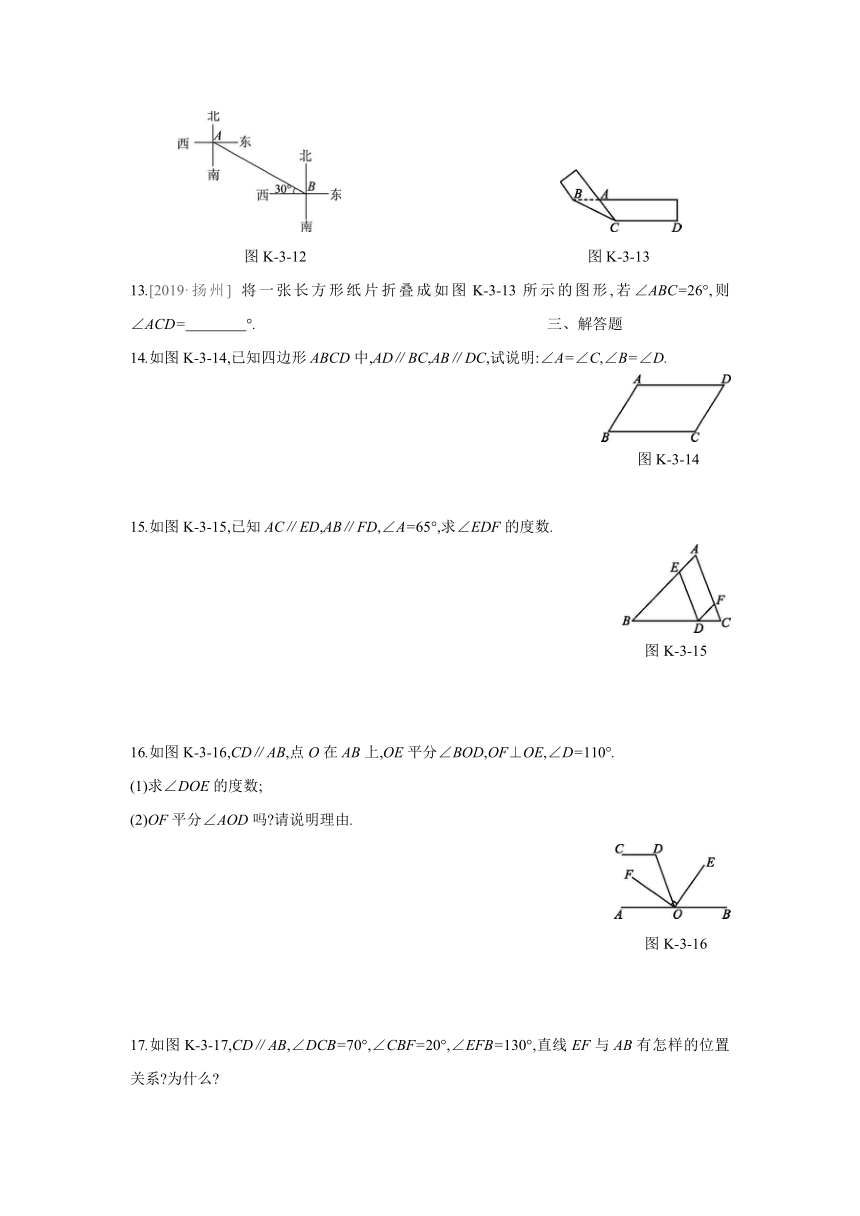
1.如图K-3-1,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,则第二个弯道处∠C的度数为
( )
A.38°
B.142°
C.152°
D.162°
图K-3-1
图K-3-2
2.如图K-3-2,由AB∥DC可以得到
( )
A.∠1=∠2
B.∠1=∠3
C.∠2=∠3
D.∠2=∠4
3.[2020·常州]
如图K-3-3,直线a,b被直线c所截,a∥b,若∠1=140°,则∠2的度数是
( )
A.30°
B.40°
C.50°
D.60°
图K-3-3
图K-3-4
4.[2019·齐齐哈尔]
如图K-3-4,直线a∥b,将一块含30°角(∠BAC=30°)的三角尺按图中所示方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为
( )
A.20°
B.30°
C.40°
D.50°
5.[2019·济南]
如图K-3-5,DE∥BC,BE平分∠ABC.若∠1=70°,则∠CBE的度数为
( )
A.20°
B.35°
C.55°
D.70°
图K-3-5
图K-3-6
6.如图K-3-6,∠1与∠2互补,∠3=135°,则∠4的度数是
( )
A.45°
B.55°
C.65°
D.75°
7.如图K-3-7,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE的度数是
( )
图K-3-7
A.16°
B.20°
C.23°
D.26°
二、填空题
8.[2019·柳州]
如图K-3-8,若AB∥CD,则在图中所标注的角中,一定相等的角是 .?
图K-3-8
图K-3-9
9.一把因损坏而倾斜的椅子,从背后看到的形状如图K-3-9,其中两组对边的平行关系没有发生变化.若∠1=75°,则∠2的度数是 .?
10.[2020·益阳]
如图K-3-10,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为 .?
图K-3-10
图K-3-11
11.如图K-3-11,已知AB∥CD,BC∥DE,∠ABC=40°,则∠CDE= °.?
12.如图K-3-12,在A处测B的方向是 .?
图K-3-12
图K-3-13
13.[2019·扬州]
将一张长方形纸片折叠成如图K-3-13所示的图形,若∠ABC=26°,则∠ACD= °.
三、解答题
14.如图K-3-14,已知四边形ABCD中,AD∥BC,AB∥DC,试说明:∠A=∠C,∠B=∠D.
图K-3-14
15.如图K-3-15,已知AC∥ED,AB∥FD,∠A=65°,求∠EDF的度数.
图K-3-15
16.如图K-3-16,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.
(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
图K-3-16
17.如图K-3-17,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,直线EF与AB有怎样的位置关系?为什么?
图K-3-17
[探究题]
如图K-3-18,已知AB∥CD,∠A=40°,P是射线AB上的一个动点(与点A不重合),CE,CF分别平分∠ACP和∠DCP,且交射线AB于点E,F.
(1)求∠ECF的度数.
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由.
(3)当∠AEC=∠ACF时,求∠APC的度数.
图K-3-18
[课堂达标]
1.B
2.D
3.[解析]
B 如图,因为∠1+∠3=180°,∠1=140°,所以∠3=180°-∠1=180°-140°=40°.
因为a∥b,所以∠2=∠3=40°.故选B.
4.[解析]
C 因为直线a∥b,所以∠1+∠BCA+∠2+∠BAC=180°.
因为∠BAC=30°,∠BCA=90°,∠1=20°,
所以∠2=40°.故选C.
5.[解析]
B 因为DE∥BC,所以∠1=∠ABC=70°.
因为BE平分∠ABC,所以∠CBE=∠ABC=35°.故选B.
6.[解析]
A 如图,因为∠1与∠2互补,所以a∥b.因为∠3=135°,所以∠5=135°.因为a∥b,所以∠4+∠5=180°,所以∠4=180°-135°=45°.故选A.
7.[解析]
B 因为AB∥EF∥CD,∠ABC=46°,∠CEF=154°,
所以∠BCD=∠ABC=46°,∠CEF+∠ECD=180°,
所以∠ECD=180°-∠CEF=26°,所以∠BCE=∠BCD-∠ECD=46°-26°=20°.故选B.
8.[答案]
∠1=∠3
[解析]
利用平行线的性质“两直线平行,同位角相等”进行判断.
9.[答案]
105°
[解析]
如图,因为AD∥BC,∠1=75°,所以∠3=∠1=75°.
因为AB∥CD,所以∠2+∠3=180°,所以∠2=180°-∠3=180°-75°=105°.
10.[答案]
132°
[解析]
因为AB⊥AE,∠CAE=42°,所以∠BAC=90°-42°=48°.
因为AB∥CD,所以∠BAC+∠ACD=180°,所以∠ACD=132°.
11.[答案]
40
[解析]
因为AB∥CD,BC∥DE,∠ABC=40°,
所以∠BCD=∠ABC=40°,∠BCD=∠CDE,故∠CDE=40°.
12.南偏东60°
13.[答案]
128
[解析]
如图,延长DC,由题意可得∠ABC=∠BCE=∠BCA=26°,则∠ACD=180°-26°-26°=128°.
14.解:因为AB∥DC,
所以∠A+∠D=180°.
因为AD∥BC,
所以∠A+∠B=180°,
所以∠B=∠D.
同理可得∠A=∠C.
15.解:因为AC∥ED,
所以∠BED=∠A=65°.
因为AB∥FD,
所以∠EDF=∠BED=65°.
16.解:(1)因为CD∥AB,
所以∠BOD=∠D=110°.
因为OE平分∠BOD,
所以∠DOE=∠BOD=55°.
(2)OF平分∠AOD.理由如下:
因为OF⊥OE,所以∠FOE=90°,所以∠DOF=90°-55°=35°.
又因为∠AOD=180°-∠BOD=70°,所以∠AOF=∠AOD-∠DOF=70°-35°=35°,
所以∠AOF=∠DOF,所以OF平分∠AOD.
17.解:EF∥AB.理由如下:
因为CD∥AB,
所以∠ABC=∠DCB=70°(两直线平行,内错角相等).
又因为∠CBF=20°,所以∠ABF=50°.
因为∠EFB=130°,
则∠ABF+∠EFB=50°+130°=180°,
所以EF∥AB(同旁内角互补,两直线平行).
[点评]
说明两直线平行可以转化为说明两角相等或互补.
[素养提升]
解:(1)因为AB∥CD,所以∠A+∠ACD=180°,
所以∠ACD=∠180°-∠A=180°-40°=140°.
因为CE平分∠ACP,CF平分∠DCP,
所以∠ECP=∠ACP,∠PCF=∠DCP,
所以∠ECF=∠ECP+∠PCF=(∠ACP+∠DCP)=∠ACD=70°.
(2)不改变.
因为AB∥CD,
所以∠AFC=∠DCF,∠APC=∠DCP.
因为CF平分∠DCP,
所以∠DCP=2∠DCF,
所以∠APC=2∠AFC.
(3)因为AB∥CD,
所以∠AEC=∠ECD.
因为∠AEC=∠ACF,所以∠ECD=∠ACF,
所以∠ACE=∠DCF.
因为CE,CF分别平分∠ACP和∠DCP,
所以∠ACP=∠DCP,
所以∠DCP=∠ACD=70°,
所以∠APC=∠DCP=70°.
[探索平行线的性质]
一、选择题
1.如图K-3-1,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,则第二个弯道处∠C的度数为
( )
A.38°
B.142°
C.152°
D.162°
图K-3-1
图K-3-2
2.如图K-3-2,由AB∥DC可以得到
( )
A.∠1=∠2
B.∠1=∠3
C.∠2=∠3
D.∠2=∠4
3.[2020·常州]
如图K-3-3,直线a,b被直线c所截,a∥b,若∠1=140°,则∠2的度数是
( )
A.30°
B.40°
C.50°
D.60°
图K-3-3
图K-3-4
4.[2019·齐齐哈尔]
如图K-3-4,直线a∥b,将一块含30°角(∠BAC=30°)的三角尺按图中所示方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为
( )
A.20°
B.30°
C.40°
D.50°
5.[2019·济南]
如图K-3-5,DE∥BC,BE平分∠ABC.若∠1=70°,则∠CBE的度数为
( )
A.20°
B.35°
C.55°
D.70°
图K-3-5
图K-3-6
6.如图K-3-6,∠1与∠2互补,∠3=135°,则∠4的度数是
( )
A.45°
B.55°
C.65°
D.75°
7.如图K-3-7,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE的度数是
( )
图K-3-7
A.16°
B.20°
C.23°
D.26°
二、填空题
8.[2019·柳州]
如图K-3-8,若AB∥CD,则在图中所标注的角中,一定相等的角是 .?
图K-3-8
图K-3-9
9.一把因损坏而倾斜的椅子,从背后看到的形状如图K-3-9,其中两组对边的平行关系没有发生变化.若∠1=75°,则∠2的度数是 .?
10.[2020·益阳]
如图K-3-10,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为 .?
图K-3-10
图K-3-11
11.如图K-3-11,已知AB∥CD,BC∥DE,∠ABC=40°,则∠CDE= °.?
12.如图K-3-12,在A处测B的方向是 .?
图K-3-12
图K-3-13
13.[2019·扬州]
将一张长方形纸片折叠成如图K-3-13所示的图形,若∠ABC=26°,则∠ACD= °.
三、解答题
14.如图K-3-14,已知四边形ABCD中,AD∥BC,AB∥DC,试说明:∠A=∠C,∠B=∠D.
图K-3-14
15.如图K-3-15,已知AC∥ED,AB∥FD,∠A=65°,求∠EDF的度数.
图K-3-15
16.如图K-3-16,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.
(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
图K-3-16
17.如图K-3-17,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,直线EF与AB有怎样的位置关系?为什么?
图K-3-17
[探究题]
如图K-3-18,已知AB∥CD,∠A=40°,P是射线AB上的一个动点(与点A不重合),CE,CF分别平分∠ACP和∠DCP,且交射线AB于点E,F.
(1)求∠ECF的度数.
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由.
(3)当∠AEC=∠ACF时,求∠APC的度数.
图K-3-18
[课堂达标]
1.B
2.D
3.[解析]
B 如图,因为∠1+∠3=180°,∠1=140°,所以∠3=180°-∠1=180°-140°=40°.
因为a∥b,所以∠2=∠3=40°.故选B.
4.[解析]
C 因为直线a∥b,所以∠1+∠BCA+∠2+∠BAC=180°.
因为∠BAC=30°,∠BCA=90°,∠1=20°,
所以∠2=40°.故选C.
5.[解析]
B 因为DE∥BC,所以∠1=∠ABC=70°.
因为BE平分∠ABC,所以∠CBE=∠ABC=35°.故选B.
6.[解析]
A 如图,因为∠1与∠2互补,所以a∥b.因为∠3=135°,所以∠5=135°.因为a∥b,所以∠4+∠5=180°,所以∠4=180°-135°=45°.故选A.
7.[解析]
B 因为AB∥EF∥CD,∠ABC=46°,∠CEF=154°,
所以∠BCD=∠ABC=46°,∠CEF+∠ECD=180°,
所以∠ECD=180°-∠CEF=26°,所以∠BCE=∠BCD-∠ECD=46°-26°=20°.故选B.
8.[答案]
∠1=∠3
[解析]
利用平行线的性质“两直线平行,同位角相等”进行判断.
9.[答案]
105°
[解析]
如图,因为AD∥BC,∠1=75°,所以∠3=∠1=75°.
因为AB∥CD,所以∠2+∠3=180°,所以∠2=180°-∠3=180°-75°=105°.
10.[答案]
132°
[解析]
因为AB⊥AE,∠CAE=42°,所以∠BAC=90°-42°=48°.
因为AB∥CD,所以∠BAC+∠ACD=180°,所以∠ACD=132°.
11.[答案]
40
[解析]
因为AB∥CD,BC∥DE,∠ABC=40°,
所以∠BCD=∠ABC=40°,∠BCD=∠CDE,故∠CDE=40°.
12.南偏东60°
13.[答案]
128
[解析]
如图,延长DC,由题意可得∠ABC=∠BCE=∠BCA=26°,则∠ACD=180°-26°-26°=128°.
14.解:因为AB∥DC,
所以∠A+∠D=180°.
因为AD∥BC,
所以∠A+∠B=180°,
所以∠B=∠D.
同理可得∠A=∠C.
15.解:因为AC∥ED,
所以∠BED=∠A=65°.
因为AB∥FD,
所以∠EDF=∠BED=65°.
16.解:(1)因为CD∥AB,
所以∠BOD=∠D=110°.
因为OE平分∠BOD,
所以∠DOE=∠BOD=55°.
(2)OF平分∠AOD.理由如下:
因为OF⊥OE,所以∠FOE=90°,所以∠DOF=90°-55°=35°.
又因为∠AOD=180°-∠BOD=70°,所以∠AOF=∠AOD-∠DOF=70°-35°=35°,
所以∠AOF=∠DOF,所以OF平分∠AOD.
17.解:EF∥AB.理由如下:
因为CD∥AB,
所以∠ABC=∠DCB=70°(两直线平行,内错角相等).
又因为∠CBF=20°,所以∠ABF=50°.
因为∠EFB=130°,
则∠ABF+∠EFB=50°+130°=180°,
所以EF∥AB(同旁内角互补,两直线平行).
[点评]
说明两直线平行可以转化为说明两角相等或互补.
[素养提升]
解:(1)因为AB∥CD,所以∠A+∠ACD=180°,
所以∠ACD=∠180°-∠A=180°-40°=140°.
因为CE平分∠ACP,CF平分∠DCP,
所以∠ECP=∠ACP,∠PCF=∠DCP,
所以∠ECF=∠ECP+∠PCF=(∠ACP+∠DCP)=∠ACD=70°.
(2)不改变.
因为AB∥CD,
所以∠AFC=∠DCF,∠APC=∠DCP.
因为CF平分∠DCP,
所以∠DCP=2∠DCF,
所以∠APC=2∠AFC.
(3)因为AB∥CD,
所以∠AEC=∠ECD.
因为∠AEC=∠ACF,所以∠ECD=∠ACF,
所以∠ACE=∠DCF.
因为CE,CF分别平分∠ACP和∠DCP,
所以∠ACP=∠DCP,
所以∠DCP=∠ACD=70°,
所以∠APC=∠DCP=70°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
