2020-2021学年人教版数学八年级下册18.2.3.1正方形的性质与判定课件(共15张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册18.2.3.1正方形的性质与判定课件(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 21:11:28 | ||
图片预览





文档简介
(共15张PPT)
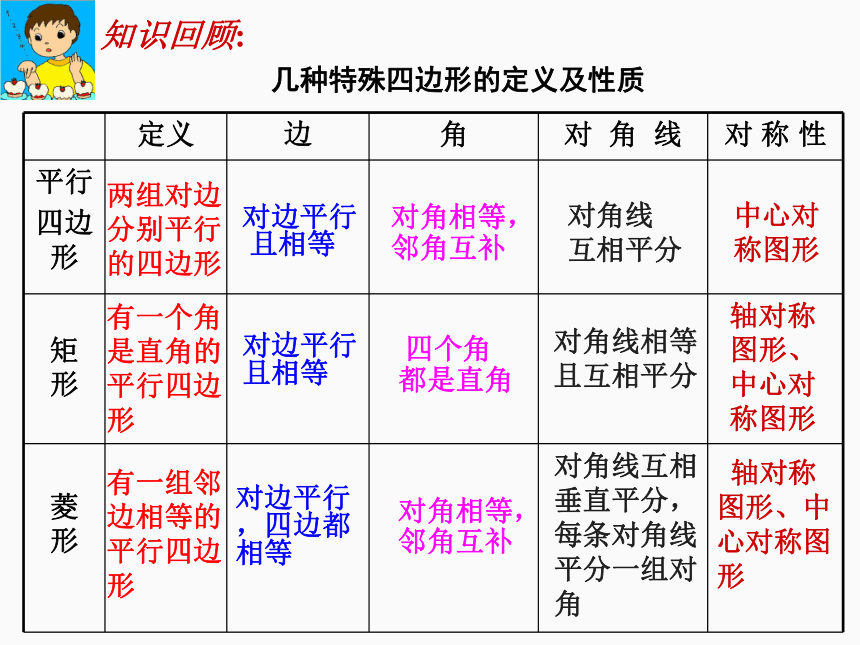
知识回顾:
定义
边
角
对
角
线
对
称
性
平行
四边形
矩
形
菱
形
几种特殊四边形的定义及性质
对边平行
且相等
对边平行
且相等
对边平行
,四边都
相等
对角相等,
邻角互补
四个角
都是直角
对角相等,邻角互补
对角线
互相平分
对角线相等
且互相平分
对角线互相
垂直平分,
每条对角线
平分一组对角
中心对
称图形
轴对称
图形、
中心对
称图形
轴对称
图形、中
心对称图形
两组对边
分别平行
的四边形
有一个角
是直角的
平行四边
形
有一组邻
边相等的
平行四边
形
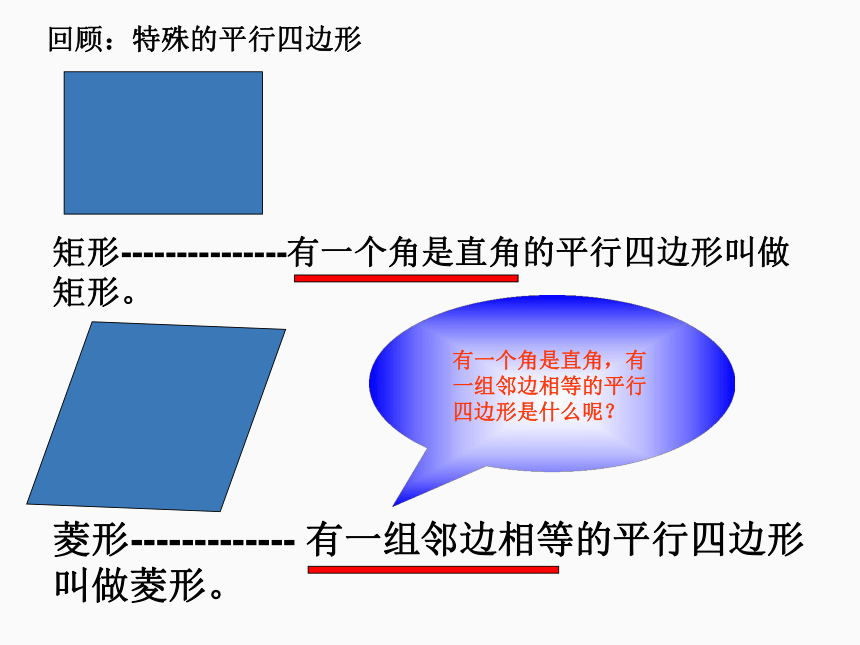
回顾:特殊的平行四边形
矩形---------------有一个角是直角的平行四边形叫做矩形。
菱形-------------
有一组邻边相等的平行四边形叫做菱形。
有一个角是直角,有一组邻边相等的平行四边形是什么呢?
探
究(一)
菱形怎样变化后就成了正方形呢?
正方形
探
究(二)
矩形怎样变化后就成了正方形呢?
尝试用你手中的长方形纸片折出一个
正方形
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形。
18.2.3正方形
学习目标
掌握正方形的概念、性质,并会运用;
理解正方形与矩形、菱形、平行四边形之间的关系
正方形的
定义:
菱形
正方形
有一个角是直角
正方形即是特殊的矩形
又是特殊的菱形。
正方形具有矩形性质的同时也具有菱形形性质。
正方形
矩形
有一组邻边相等
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的包含关系
想一想
正方形的性质
四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
边----
角----
对角线----
菱形的性质
矩形的性质
对称性------
是轴对称图形,也是中心对称图形
总结:平行四边形、矩形、菱形、正方形的对称性
平行四边形
中心对称图形
(对角线的交点)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(四条)
求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.
△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
A
B
C
D
O
例1已知:如图,四边形ABCD是正
方形,对角线AC、BD相交于点O
学而时习之
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、
1、矩形、菱形、正方形都具有的性质是(
)
A.对角线相等
B.对角线互相平分
C.对角线平分一组对角
D.对角线互相垂直
2、正方形具有而菱形不一定具有的性质
(
)
A
对角线互相平分
B
对角线相等
C
对角线互相垂直
D
对角线平分一组对角
3、正方形的一条对角线长为4,则这个正方形的面积是(
)
A
8
B
4
C
8
D
16
B
B
A
.四边形ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?
A
D
A
B
C
E
活动
解:
连接AC.
∵
四边形ABCD是正方形
∴
∠B=90°,AB=BC
∵
EC=50m,EB=30m
∴
S正方形ABCD=(40
)2=1600(m2)
∴
∴
根据图形所具有的性质,在下表相应的空格中打”√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
体会正方形的完美
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。
知识回顾:
定义
边
角
对
角
线
对
称
性
平行
四边形
矩
形
菱
形
几种特殊四边形的定义及性质
对边平行
且相等
对边平行
且相等
对边平行
,四边都
相等
对角相等,
邻角互补
四个角
都是直角
对角相等,邻角互补
对角线
互相平分
对角线相等
且互相平分
对角线互相
垂直平分,
每条对角线
平分一组对角
中心对
称图形
轴对称
图形、
中心对
称图形
轴对称
图形、中
心对称图形
两组对边
分别平行
的四边形
有一个角
是直角的
平行四边
形
有一组邻
边相等的
平行四边
形
回顾:特殊的平行四边形
矩形---------------有一个角是直角的平行四边形叫做矩形。
菱形-------------
有一组邻边相等的平行四边形叫做菱形。
有一个角是直角,有一组邻边相等的平行四边形是什么呢?
探
究(一)
菱形怎样变化后就成了正方形呢?
正方形
探
究(二)
矩形怎样变化后就成了正方形呢?
尝试用你手中的长方形纸片折出一个
正方形
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形。
18.2.3正方形
学习目标
掌握正方形的概念、性质,并会运用;
理解正方形与矩形、菱形、平行四边形之间的关系
正方形的
定义:
菱形
正方形
有一个角是直角
正方形即是特殊的矩形
又是特殊的菱形。
正方形具有矩形性质的同时也具有菱形形性质。
正方形
矩形
有一组邻边相等
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的包含关系
想一想
正方形的性质
四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
边----
角----
对角线----
菱形的性质
矩形的性质
对称性------
是轴对称图形,也是中心对称图形
总结:平行四边形、矩形、菱形、正方形的对称性
平行四边形
中心对称图形
(对角线的交点)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(四条)
求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.
△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
A
B
C
D
O
例1已知:如图,四边形ABCD是正
方形,对角线AC、BD相交于点O
学而时习之
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、
1、矩形、菱形、正方形都具有的性质是(
)
A.对角线相等
B.对角线互相平分
C.对角线平分一组对角
D.对角线互相垂直
2、正方形具有而菱形不一定具有的性质
(
)
A
对角线互相平分
B
对角线相等
C
对角线互相垂直
D
对角线平分一组对角
3、正方形的一条对角线长为4,则这个正方形的面积是(
)
A
8
B
4
C
8
D
16
B
B
A
.四边形ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?
A
D
A
B
C
E
活动
解:
连接AC.
∵
四边形ABCD是正方形
∴
∠B=90°,AB=BC
∵
EC=50m,EB=30m
∴
S正方形ABCD=(40
)2=1600(m2)
∴
∴
根据图形所具有的性质,在下表相应的空格中打”√”
平行四边形
矩形
菱形
正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
体会正方形的完美
正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。
