2020-2021学年苏科版八年级数学下册9.3 平行四边形的判定(1)提优训练(Word版,含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学下册9.3 平行四边形的判定(1)提优训练(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 101.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览


文档简介
9.3
平行四边形(2)提优训练
一、选择题
1.(2020衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AB∥DC,AD=BC
D.OA=OC,OB=OD
第1题
第3题
第6题
2.(2020春哈尔滨期末)四边形ABCD中,从∠A,∠B,∠C,∠D的度数之比中,能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4
B.2:3:2:3
C.2:2:3:3
D.1:2:2:3
3.(2020河池)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
4.(2020春海淀校级期中)在四边形ABCD中,对角线AC、BD相交于O,给出下列四个条件:①AB∥CD;②OA=OC;③AD=BC;④∠BAD=∠BCD,任取两个条件,可得出四边形ABCD是平行四边形这一结论的情况有( )
A.5种
B.4种
C.3种
D.2种
5.(2019鄂城期中)在平面直角坐标系中,点O、B、D的坐标分别是(0,0)、(5,0)、(2,3),若存在点C,使得以点O、B、D、C为顶点的四边形是平行四边形,则下列给出的C点坐标中,错误的是( )
A.(3,﹣3)
B.(﹣3,3)
C.(3,5)
D.(7,3)
6.(2019威海)如图,E是□ABCD边AD延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE
B.DF=CF
C.∠AEB=∠BCD
D.∠AEC=∠CBD
二、填空题
7.(2020鸡西)如图,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件
,使四边形ABCD是平行四边形(填一个即可).
第7题
第9题
第10题
8.(2020春张家港期中)一个四边形的边长依次为a、b、c、d,且a2+b2+c2+d2-2ac-2bd=0,则这个四边形的形状是
,依据是
.
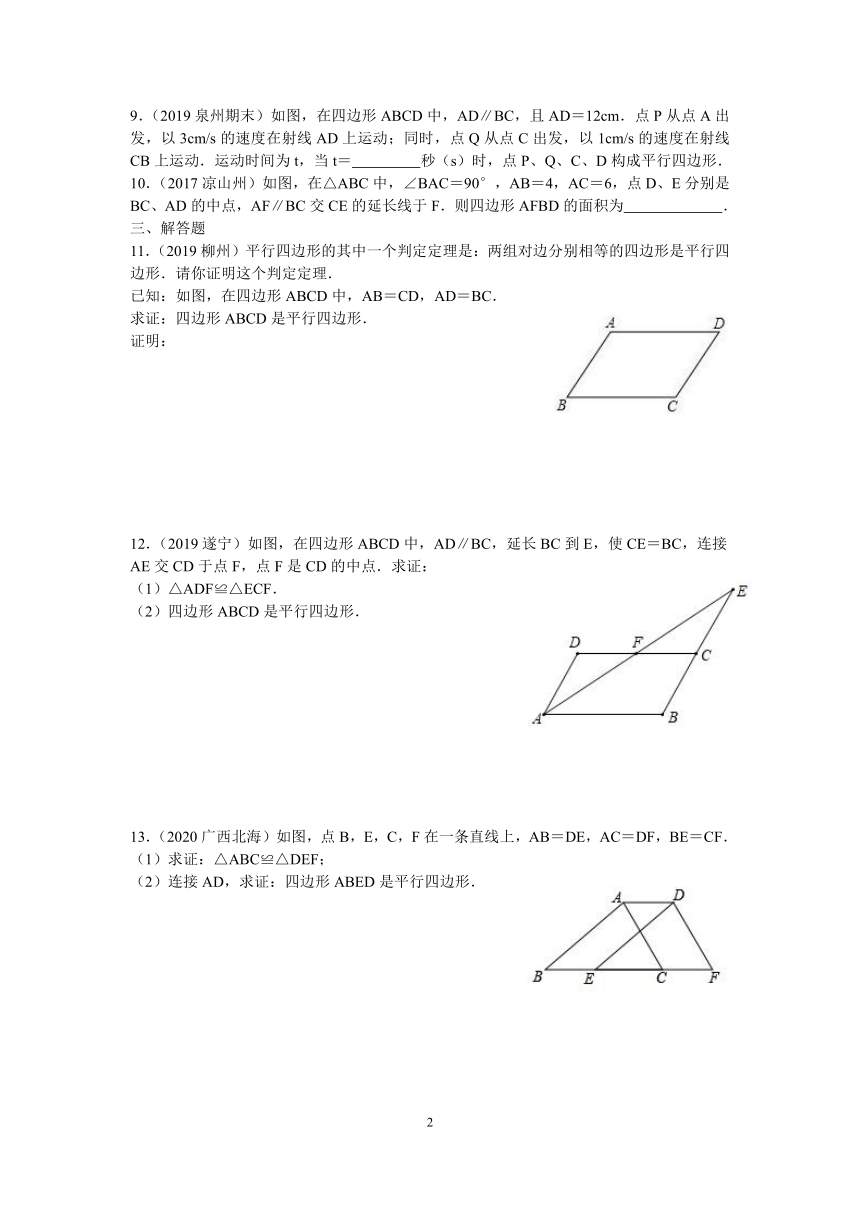
9.(2019泉州期末)如图,在四边形ABCD中,AD∥BC,且AD=12cm.点P从点A出发,以3cm/s的速度在射线AD上运动;同时,点Q从点C出发,以1cm/s的速度在射线CB上运动.运动时间为t,当t=
秒(s)时,点P、Q、C、D构成平行四边形.
10.(2017凉山州)如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于F.则四边形AFBD的面积为
.
三、解答题
11.(2019柳州)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:
12.(2019遂宁)如图,在四边形ABCD中,AD∥BC,延长BC到E,使CE=BC,连接AE交CD于点F,点F是CD的中点.求证:
(1)△ADF≌△ECF.
(2)四边形ABCD是平行四边形.
13.(2020广西北海)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
14.(2019本溪)如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE=DA,连接AE.
(1)求证:AE=BC;
(2)若AB=3,CD=1,求四边形ABCE的面积.
15.(2020南海区一模)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
求证:(1)AC=EF;
(2)四边形ADFE是平行四边形;
(3)AC⊥DF.
16.(2019遵化二模)如图,在四边形ABCD中,E是BC上一点,AE交BD于点O,AD=BD,∠ADB=∠EDC,DE=DC.
(1)求证:△ADE≌△BDC;
(2)若∠AEB=36°,求∠EDC;
(3)若OB=OE,求证:四边形ABCD是平行四边形.
参考答案
一、选择题
1—6
CBBDCC
二、填空题
7.AD=BC
8.平行四边形;两组对边分别相等的四边形是平行四边形
9.3或6
10.12
三、解答题
11.证明:连接AC,如图所示:
在△ABC和△CDA中,
∵,
∴△ABC≌△CDA(SSS),
∴∠BAC=∠DCA,∠ACB=∠CAD,
∴AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形.
12.证明:(1)∵AD∥BC,
∴∠DAF=∠E,
∵点F是CD的中点,
∴DF=CF,
在△ADF与△ECF中,
∵,
∴△ADF≌△ECF(AAS);
(2)∵△ADF≌△ECF,
∴AD=EC,
∵CE=BC,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形.
13.(1)证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,
∵,
∴△ABC≌△DEF(SSS);
(2)证明:由(1)得:△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE,
又∵AB=DE,
∴四边形ABED是平行四边形.
14.证明:(1)∵AB∥CD,∠B=45°
∴∠C+∠B=180°
∴∠C=135°
∵DE=DA,AD⊥CD
∴∠E=45°
∵∠E+∠C=180°
∴AE∥BC,且AB∥CD
∴四边形ABCE是平行四边形
∴AE=BC
(2)∵四边形ABCE是平行四边形
∴AB=CE=3
∴AD=DE=AB-CD=2
∴四边形ABCE的面积=3×2=6
15.证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF,AB=AE,
∴AF=BC,
在Rt△AFE和Rt△BCA中,
∵,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形;
(3)∵∠EAC=∠EAF+∠BAC=60°+30°=90°,
∵四边形ADFE是平行四边形,
∴AE∥FD,
∴∠EAC=∠AGD=90°,
∴AC⊥DF.
16.(1)证明:∵∠ADB=∠EDC,
∴∠ADE=∠BDC,
在△ADE和△BDC中,
∵,
∴△ADE≌△BDC(SAS);
(2)解:∵△ADE≌△BDC,
∴∠AED=∠C,
∵∠AEB=36°,
∴∠AED=∠DEC=∠C=(180°-36°)=72°,
∴∠EDC=180°-2×72°=36°;
(3)证明:∵OB=OE,
∴∠OBE=∠OEB,
∵∠DAE=∠OBE,
∴∠OEB=∠DAE,
∴AD∥BC,
∴∠ADB=∠OBE,
∴∠ADB=∠DAE,
∴OA=OD,
∴AE=BD,
∵AD=BD,
∴AE=AD,
∵△ADE≌△BDC,
∴AE=BC,
∴AD=BC,
又∵AD∥BC,
∴四边形ABCD是平行四边形.
6
平行四边形(2)提优训练
一、选择题
1.(2020衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AB∥DC,AD=BC
D.OA=OC,OB=OD
第1题
第3题
第6题
2.(2020春哈尔滨期末)四边形ABCD中,从∠A,∠B,∠C,∠D的度数之比中,能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4
B.2:3:2:3
C.2:2:3:3
D.1:2:2:3
3.(2020河池)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
4.(2020春海淀校级期中)在四边形ABCD中,对角线AC、BD相交于O,给出下列四个条件:①AB∥CD;②OA=OC;③AD=BC;④∠BAD=∠BCD,任取两个条件,可得出四边形ABCD是平行四边形这一结论的情况有( )
A.5种
B.4种
C.3种
D.2种
5.(2019鄂城期中)在平面直角坐标系中,点O、B、D的坐标分别是(0,0)、(5,0)、(2,3),若存在点C,使得以点O、B、D、C为顶点的四边形是平行四边形,则下列给出的C点坐标中,错误的是( )
A.(3,﹣3)
B.(﹣3,3)
C.(3,5)
D.(7,3)
6.(2019威海)如图,E是□ABCD边AD延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE
B.DF=CF
C.∠AEB=∠BCD
D.∠AEC=∠CBD
二、填空题
7.(2020鸡西)如图,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件
,使四边形ABCD是平行四边形(填一个即可).
第7题
第9题
第10题
8.(2020春张家港期中)一个四边形的边长依次为a、b、c、d,且a2+b2+c2+d2-2ac-2bd=0,则这个四边形的形状是
,依据是
.
9.(2019泉州期末)如图,在四边形ABCD中,AD∥BC,且AD=12cm.点P从点A出发,以3cm/s的速度在射线AD上运动;同时,点Q从点C出发,以1cm/s的速度在射线CB上运动.运动时间为t,当t=
秒(s)时,点P、Q、C、D构成平行四边形.
10.(2017凉山州)如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于F.则四边形AFBD的面积为
.
三、解答题
11.(2019柳州)平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:
12.(2019遂宁)如图,在四边形ABCD中,AD∥BC,延长BC到E,使CE=BC,连接AE交CD于点F,点F是CD的中点.求证:
(1)△ADF≌△ECF.
(2)四边形ABCD是平行四边形.
13.(2020广西北海)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
14.(2019本溪)如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE=DA,连接AE.
(1)求证:AE=BC;
(2)若AB=3,CD=1,求四边形ABCE的面积.
15.(2020南海区一模)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
求证:(1)AC=EF;
(2)四边形ADFE是平行四边形;
(3)AC⊥DF.
16.(2019遵化二模)如图,在四边形ABCD中,E是BC上一点,AE交BD于点O,AD=BD,∠ADB=∠EDC,DE=DC.
(1)求证:△ADE≌△BDC;
(2)若∠AEB=36°,求∠EDC;
(3)若OB=OE,求证:四边形ABCD是平行四边形.
参考答案
一、选择题
1—6
CBBDCC
二、填空题
7.AD=BC
8.平行四边形;两组对边分别相等的四边形是平行四边形
9.3或6
10.12
三、解答题
11.证明:连接AC,如图所示:
在△ABC和△CDA中,
∵,
∴△ABC≌△CDA(SSS),
∴∠BAC=∠DCA,∠ACB=∠CAD,
∴AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形.
12.证明:(1)∵AD∥BC,
∴∠DAF=∠E,
∵点F是CD的中点,
∴DF=CF,
在△ADF与△ECF中,
∵,
∴△ADF≌△ECF(AAS);
(2)∵△ADF≌△ECF,
∴AD=EC,
∵CE=BC,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形.
13.(1)证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,
∵,
∴△ABC≌△DEF(SSS);
(2)证明:由(1)得:△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE,
又∵AB=DE,
∴四边形ABED是平行四边形.
14.证明:(1)∵AB∥CD,∠B=45°
∴∠C+∠B=180°
∴∠C=135°
∵DE=DA,AD⊥CD
∴∠E=45°
∵∠E+∠C=180°
∴AE∥BC,且AB∥CD
∴四边形ABCE是平行四边形
∴AE=BC
(2)∵四边形ABCE是平行四边形
∴AB=CE=3
∴AD=DE=AB-CD=2
∴四边形ABCE的面积=3×2=6
15.证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF,AB=AE,
∴AF=BC,
在Rt△AFE和Rt△BCA中,
∵,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形;
(3)∵∠EAC=∠EAF+∠BAC=60°+30°=90°,
∵四边形ADFE是平行四边形,
∴AE∥FD,
∴∠EAC=∠AGD=90°,
∴AC⊥DF.
16.(1)证明:∵∠ADB=∠EDC,
∴∠ADE=∠BDC,
在△ADE和△BDC中,
∵,
∴△ADE≌△BDC(SAS);
(2)解:∵△ADE≌△BDC,
∴∠AED=∠C,
∵∠AEB=36°,
∴∠AED=∠DEC=∠C=(180°-36°)=72°,
∴∠EDC=180°-2×72°=36°;
(3)证明:∵OB=OE,
∴∠OBE=∠OEB,
∵∠DAE=∠OBE,
∴∠OEB=∠DAE,
∴AD∥BC,
∴∠ADB=∠OBE,
∴∠ADB=∠DAE,
∴OA=OD,
∴AE=BD,
∵AD=BD,
∴AE=AD,
∵△ADE≌△BDC,
∴AE=BC,
∴AD=BC,
又∵AD∥BC,
∴四边形ABCD是平行四边形.
6
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
