相似三角形判定-探究2
图片预览




文档简介
(共18张PPT)
已知在△ 和△ 中,有
则△ 和△ 是何种关系?为什么?
练习:
思考:1.如果去掉一组对应边的比 ,还相似吗?若不成立,请举反例。若成立,请证明。
3.这一组对应角加在图中什么位置,结论才能成立?自己构图观察,如果不成立,请举反例说明;若成立,请加以证明。
2.若不相似你认为需要加什么条件才有可能相似?
问题探究
A
B
C
A1
B1
C1
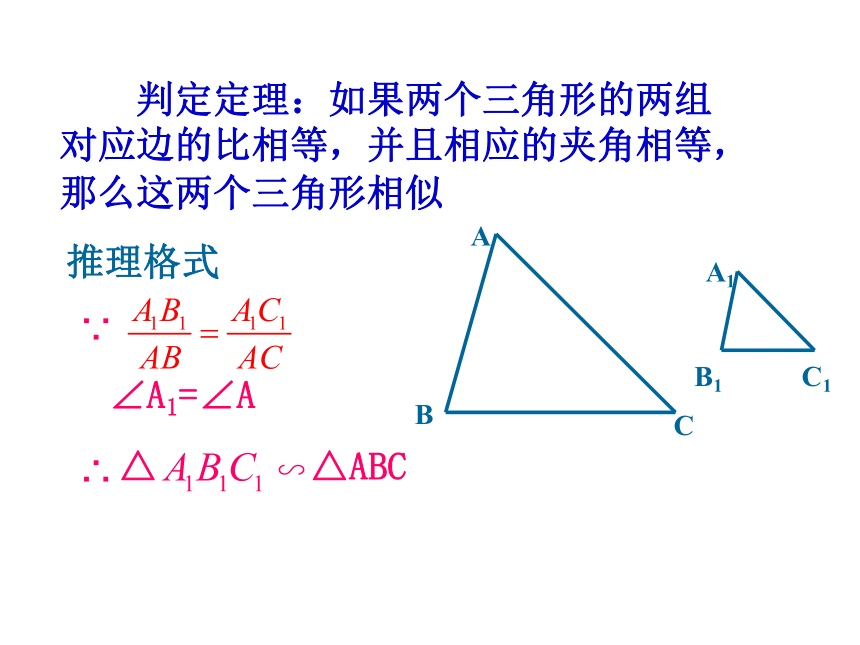
判定定理:如果两个三角形的两组
对应边的比相等,并且相应的夹角相等,
那么这两个三角形相似
∠A1=∠A
∵
△
△ABC
∽
∴
推理格式
∠A1=∠A
∵
△
△ABC
∽
∴
A
B
C
A1
B1
C1
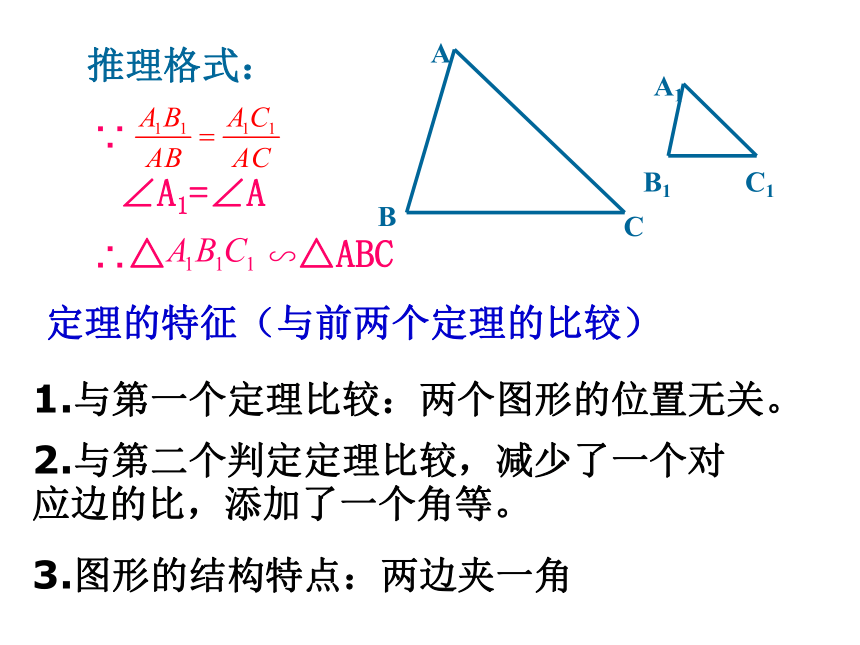
推理格式:
1.与第一个定理比较:两个图形的位置无关。
3.图形的结构特点:两边夹一角
2.与第二个判定定理比较,减少了一个对应边的比,添加了一个角等。
定理的特征(与前两个定理的比较)
(3)
练1.依据下列条件,判定
是否相似,并说明理由。
(2)
(1)
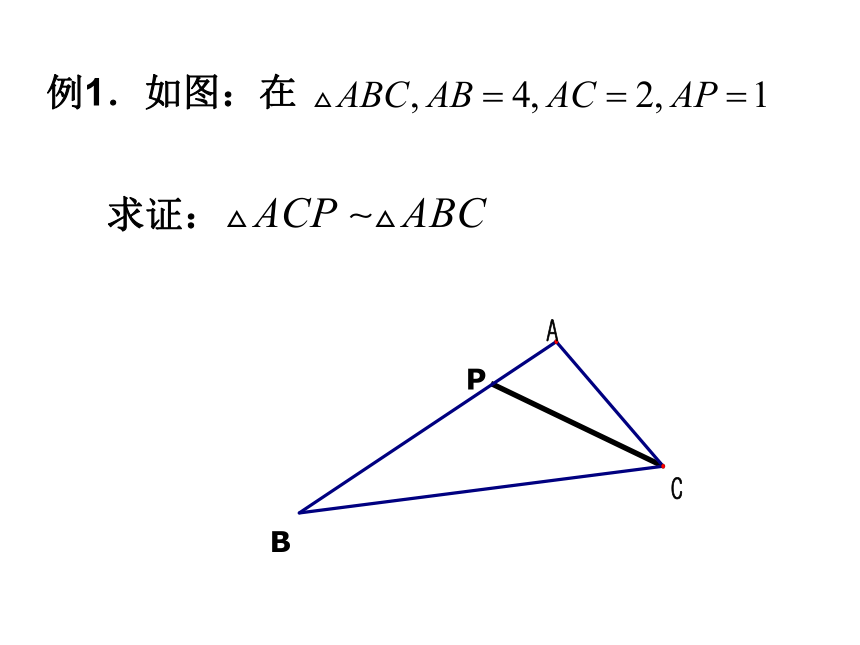
例1.如图:在
求证:
B
P
例11.已知:
上一点,连结CP,当PA=___时,
B
P
1
例12.如图:
上一点,连结CP,当AC,AB,AP数量
上满足__________时,
B
P
例13.如图:已知AB=4,AC=2,AC1=1
P是AB上一动点,当PA=________时,
2
例3.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与△ABC相似,则点P的坐标是__________________.
y
·A
B
C
x
·
·
O
·P
点P在y轴正半轴上远动,改为点P在y轴上远动,P点的坐标有几个
6.如图,在正方形格点图中,
画一个格点三角形
(顶点都在小正方形格点上)与
相似。
2.本节课你经历了什么过程?
1.你获得了什么知识?学会了什么方法?
3.这节课你最深刻的体会是什么
书P55. 2,3
书P56.8.10
相似三角形判定
∠A1=∠A
∵
△
△ABC
∽
∴
A
B
C
B1
A1
C1
已知在△ 和△ 中,有
则△ 和△ 是何种关系?为什么?
练习:
思考:1.如果去掉一组对应边的比 ,还相似吗?若不成立,请举反例。若成立,请证明。
3.这一组对应角加在图中什么位置,结论才能成立?自己构图观察,如果不成立,请举反例说明;若成立,请加以证明。
2.若不相似你认为需要加什么条件才有可能相似?
问题探究
A
B
C
A1
B1
C1
判定定理:如果两个三角形的两组
对应边的比相等,并且相应的夹角相等,
那么这两个三角形相似
∠A1=∠A
∵
△
△ABC
∽
∴
推理格式
∠A1=∠A
∵
△
△ABC
∽
∴
A
B
C
A1
B1
C1
推理格式:
1.与第一个定理比较:两个图形的位置无关。
3.图形的结构特点:两边夹一角
2.与第二个判定定理比较,减少了一个对应边的比,添加了一个角等。
定理的特征(与前两个定理的比较)
(3)
练1.依据下列条件,判定
是否相似,并说明理由。
(2)
(1)
例1.如图:在
求证:
B
P
例11.已知:
上一点,连结CP,当PA=___时,
B
P
1
例12.如图:
上一点,连结CP,当AC,AB,AP数量
上满足__________时,
B
P
例13.如图:已知AB=4,AC=2,AC1=1
P是AB上一动点,当PA=________时,
2
例3.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与△ABC相似,则点P的坐标是__________________.
y
·A
B
C
x
·
·
O
·P
点P在y轴正半轴上远动,改为点P在y轴上远动,P点的坐标有几个
6.如图,在正方形格点图中,
画一个格点三角形
(顶点都在小正方形格点上)与
相似。
2.本节课你经历了什么过程?
1.你获得了什么知识?学会了什么方法?
3.这节课你最深刻的体会是什么
书P55. 2,3
书P56.8.10
相似三角形判定
∠A1=∠A
∵
△
△ABC
∽
∴
A
B
C
B1
A1
C1
