广西钦州第四高级中学校2020-2021学年高一下学期4月第五周周测数学试题 Word版含答案
文档属性
| 名称 | 广西钦州第四高级中学校2020-2021学年高一下学期4月第五周周测数学试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 243.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览



文档简介
____________________________________________________________________________________________
广西钦州市第四中学2021年春季学期高一数学第五周周测试卷一.选择题
1.在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,AA1=4,AB=2,,E为BC中点,平面α过点E且与平面BDD1垂直,CC1∥α,则α被此直四棱柱截得的截面面积为( )
A.1 B.2 C.4 D.6
2.如图,在正方体ABCD﹣A′B′C′D′中,E、F分别为平面ABCD和平面A′B′C′D′的中心,则正方体的六个面中与EF平行的平面有( )
A.4个 B.3个 C.2个 D.1个
3.如图,在以下四个正方体中,直线MN与平面ABC平行的是( )
A. B.
C. D.
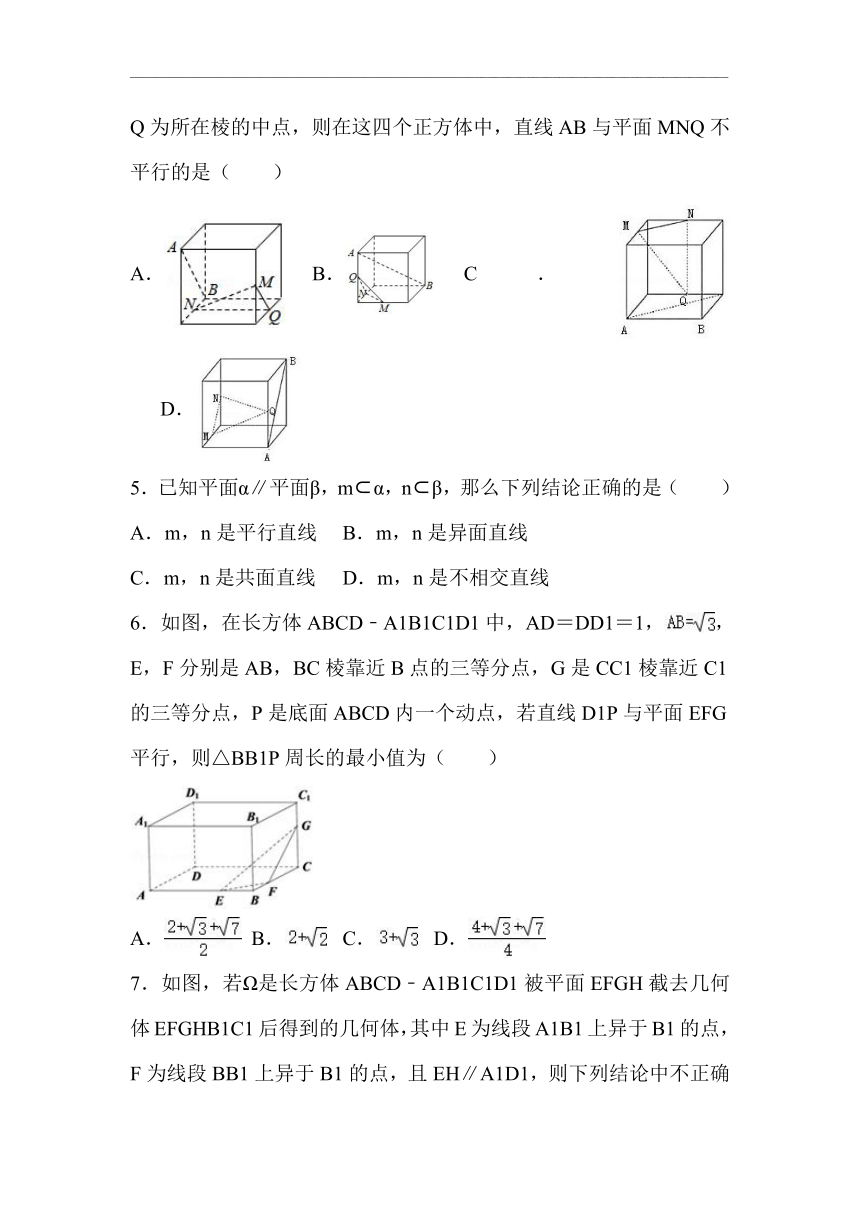
4.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A. B. C. D.
5.已知平面α∥平面β,m?α,n?β,那么下列结论正确的是( )
A.m,n是平行直线 B.m,n是异面直线
C.m,n是共面直线 D.m,n是不相交直线
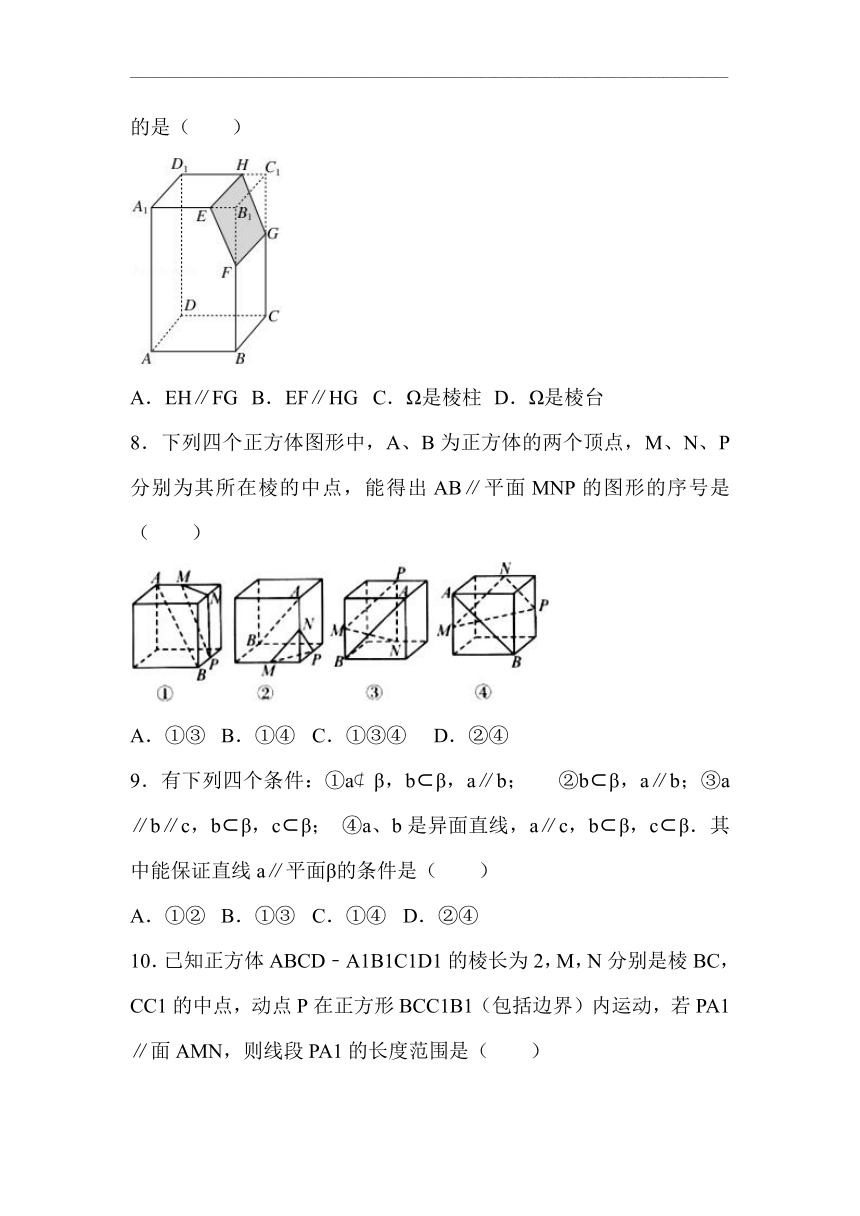
6.如图,在长方体ABCD﹣A1B1C1D1中,AD=DD1=1,,E,F分别是AB,BC棱靠近B点的三等分点,G是CC1棱靠近C1的三等分点,P是底面ABCD内一个动点,若直线D1P与平面EFG平行,则△BB1P周长的最小值为( )
A. B. C. D.
7.如图,若Ω是长方体ABCD﹣A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
A.EH∥FG B.EF∥HG C.Ω是棱柱 D.Ω是棱台
8.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
A.①③ B.①④ C.①③④ D.②④
9.有下列四个条件:①a?β,b?β,a∥b; ②b?β,a∥b;③a∥b∥c,b?β,c?β; ④a、b是异面直线,a∥c,b?β,c?β.其中能保证直线a∥平面β的条件是( )
A.①② B.①③ C.①④ D.②④
10.已知正方体ABCD﹣A1B1C1D1的棱长为2,M,N分别是棱BC,CC1的中点,动点P在正方形BCC1B1(包括边界)内运动,若PA1∥面AMN,则线段PA1的长度范围是( )
A.[2,] B.[2,3] C.[,3] D.[,]
11.如图,在三棱锥A﹣BCD中,E,F分别为AB,AD的中点,过EF的平面截三棱锥得到的截面为EFHG.则下列结论中不一定成立的是( )
A.EF∥GH B.BD∥GH C.GH∥平面ABD D.AC∥平面EFHG
12.在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,P是上底面A1B1C1D1内一点,若AP∥平面BDEF,则线段AP长度的取值范围是( )
A.[,] B.[,] C.[,] D.[,]
二.填空题
13.已知平面α∥平面β,点S是α,β外一点过S的两条直线AB,CD分别交α于A,C,交β于B,D,若SA=2,SB=4,CD=6,则SC= .
14.已知四棱锥S﹣ABCD的底面是边长为4的正方形,SD⊥面ABCD,点M、N分别是AD、CD的中点,P为SD上一点,且SD=3PD=3,H为正方形ABCD内一点,若SH∥面PMN,则SH的最小值为 .
15.已知棱长为2的正方体ABCD﹣A1B1C1D1中,E在棱AD上,且2AE=DE,则过点B1且与平面A1BE平行的正方体的截面面积为 .
16.如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,且E为CD的中点,M、N分别是AD,BE的中点,将△ADE沿AE折起,则下列说法正确的是 .(写出所有正确说法的序号)
①不论D折至何位置(不在平面ABC内,都有MN∥平面DEC;
②不论D折至何位置(不在平面ABC内)都有MN⊥AE;
③不论D折至何位置(不在平面ABC内),都有MN∥AB;
④不论D折至何位置(不在平面ABC内),都有EC不垂直AD.
三.解答题
17.如图,已知点P在四面体A﹣BCD的棱AB(不含A,B两点)上运动,过点P作四面体A﹣BCD的一个与AC,BD都平行的截面.
(1)试画出该截面(不写作法),判断该截面的形状,并证明你的结论;
(2)当P为AB的中点,且AC=8,BD=6,AC与BD所成角为60°时,求截面的面积.
18.如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,且AD⊥DC,AD∥BC,PD⊥平面ABCD,AD=4,BC=CD=2,点E为线段PA的靠近点P的三等分点.
(1)求证:PC∥平面BDE;
(2)若异面直线PA与BC所成的角为45°,求多面体BCDEP的体积.
19.在如图所示的几何体中,四边形ABCD是菱形,∠BAD=120°,AE⊥平面ABCD,AE∥CF.
(1)求证:DF∥平面ABE;
(2)若AD=AE=2CF=2,求该几何体的表面积.
20.如图,P为圆锥的顶点,O是圆锥底面的圆心,AC,BD为圆锥底面的两条直径,M为母线PD上一点,连接MA,MO,MC.
(1)若M为PD的中点,证明:PB∥平面MAC;
(2)若PB∥平面MAC,证明:M为PD的中点.
参考答案
一.选择题
1.C2.A3.D4.B5.D6.A7.D8.B9.C10.D11.D12.B
二.填空题
13.2或6.14.3.15.,16.①②.
三.解答题
17.(1)画出过点P且平行于AC和BD的截面PQRS,如图所示:
该截面PQRS是平行四边形,证明如下:
由AC∥平面PQRS,AC?平面ABC,平面ABC∩平面PQRS=PQ,所以AC∥PQ;
同理,AC∥SR;所以PQ∥SR.
同理,PS∥QR,所以四边形PQRS是平行四边形.
(2)当P为AB的中点时,PQ∥AC,且PQ=AC=4;
PS∥BD,且PS=BD=3;
由AC与BD所成角为60°,所以PS、PQ所成的角也是60°,
所以截面四边形PQRS的面积为
S平行四边形PQRS=PS?PQ?sin60°=3×4×=6.
18.(1)连接AC交BD于点O,连接OE.
因 ABCD是直角梯形,且AD⊥DC,AD∥BC,AD=4,BC=2,
所以△ADO和△CBO相似,且有==2;
又点E为线段PA的靠近点P的三等分点,有=2,
所以有=;
所以OE∥CP.
又OE?平面BDE,
所以PC∥平面BDE.
(2)直线PA与BC所成的角为45°,即∠PAD=45°,
又AD=4,PD⊥平面ABCD,所以PD=AD=4.
计算得V四棱锥P﹣ABCD=×(2+4)×2×4=8,
V三棱锥E﹣ABD=××4×2××4=.
所以多面体BCDEP的体积为V多面体BCDEP=V四棱锥P﹣ABCD﹣V三棱锥E﹣ABD=8﹣=.
19.(1)证明:因为AE∥CF,CF?平面ABE,
所以CF∥平面ABE,
因为四边形ABCD是菱形,
所以CD∥AB,
由于CD?平面ABE,
所以CD∥平面ABE,
又CF∩CD=C,
所以平面CDF∥平面ABE,
又DF?平面CDF,
所以DF∥平面ABE.
(2)由AE∥CF,知A,C,F,E四点共面,
连接AC,于是该几何体是由两个相同的四棱锥B﹣ACFE,D﹣ACFE构成的,
由题意知,S△ABE==2,S△ABC==,S△BCF==1,
在△BEF中,EF=,BE=2,BF=,S△BEF==,
所以该几何体的表面积为2×(S△ABE+S△ABC+S△BCF+S△BEF)=6+2+2.
20.证明:(1)若M为PD的中点,由BD为圆锥底面的直径,有O为BD的中点,
则在△PBD中有MO∥PB,
又MO?平面MAC,PB?平面MAC,
则有PB∥平面MAC.
(2)若PB∥平面MAC,由PB?平面PBD,平面PBD∩平面MAC=MO,
可得PB∥MO,
所以在△PBD中,=,
又O为BD的中点,则有DM=MP,
则M为PD的中点.
广西钦州市第四中学2021年春季学期高一数学第五周周测试卷一.选择题
1.在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,AA1=4,AB=2,,E为BC中点,平面α过点E且与平面BDD1垂直,CC1∥α,则α被此直四棱柱截得的截面面积为( )
A.1 B.2 C.4 D.6
2.如图,在正方体ABCD﹣A′B′C′D′中,E、F分别为平面ABCD和平面A′B′C′D′的中心,则正方体的六个面中与EF平行的平面有( )
A.4个 B.3个 C.2个 D.1个
3.如图,在以下四个正方体中,直线MN与平面ABC平行的是( )
A. B.
C. D.
4.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A. B. C. D.
5.已知平面α∥平面β,m?α,n?β,那么下列结论正确的是( )
A.m,n是平行直线 B.m,n是异面直线
C.m,n是共面直线 D.m,n是不相交直线
6.如图,在长方体ABCD﹣A1B1C1D1中,AD=DD1=1,,E,F分别是AB,BC棱靠近B点的三等分点,G是CC1棱靠近C1的三等分点,P是底面ABCD内一个动点,若直线D1P与平面EFG平行,则△BB1P周长的最小值为( )
A. B. C. D.
7.如图,若Ω是长方体ABCD﹣A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
A.EH∥FG B.EF∥HG C.Ω是棱柱 D.Ω是棱台
8.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
A.①③ B.①④ C.①③④ D.②④
9.有下列四个条件:①a?β,b?β,a∥b; ②b?β,a∥b;③a∥b∥c,b?β,c?β; ④a、b是异面直线,a∥c,b?β,c?β.其中能保证直线a∥平面β的条件是( )
A.①② B.①③ C.①④ D.②④
10.已知正方体ABCD﹣A1B1C1D1的棱长为2,M,N分别是棱BC,CC1的中点,动点P在正方形BCC1B1(包括边界)内运动,若PA1∥面AMN,则线段PA1的长度范围是( )
A.[2,] B.[2,3] C.[,3] D.[,]
11.如图,在三棱锥A﹣BCD中,E,F分别为AB,AD的中点,过EF的平面截三棱锥得到的截面为EFHG.则下列结论中不一定成立的是( )
A.EF∥GH B.BD∥GH C.GH∥平面ABD D.AC∥平面EFHG
12.在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,P是上底面A1B1C1D1内一点,若AP∥平面BDEF,则线段AP长度的取值范围是( )
A.[,] B.[,] C.[,] D.[,]
二.填空题
13.已知平面α∥平面β,点S是α,β外一点过S的两条直线AB,CD分别交α于A,C,交β于B,D,若SA=2,SB=4,CD=6,则SC= .
14.已知四棱锥S﹣ABCD的底面是边长为4的正方形,SD⊥面ABCD,点M、N分别是AD、CD的中点,P为SD上一点,且SD=3PD=3,H为正方形ABCD内一点,若SH∥面PMN,则SH的最小值为 .
15.已知棱长为2的正方体ABCD﹣A1B1C1D1中,E在棱AD上,且2AE=DE,则过点B1且与平面A1BE平行的正方体的截面面积为 .
16.如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,且E为CD的中点,M、N分别是AD,BE的中点,将△ADE沿AE折起,则下列说法正确的是 .(写出所有正确说法的序号)
①不论D折至何位置(不在平面ABC内,都有MN∥平面DEC;
②不论D折至何位置(不在平面ABC内)都有MN⊥AE;
③不论D折至何位置(不在平面ABC内),都有MN∥AB;
④不论D折至何位置(不在平面ABC内),都有EC不垂直AD.
三.解答题
17.如图,已知点P在四面体A﹣BCD的棱AB(不含A,B两点)上运动,过点P作四面体A﹣BCD的一个与AC,BD都平行的截面.
(1)试画出该截面(不写作法),判断该截面的形状,并证明你的结论;
(2)当P为AB的中点,且AC=8,BD=6,AC与BD所成角为60°时,求截面的面积.
18.如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,且AD⊥DC,AD∥BC,PD⊥平面ABCD,AD=4,BC=CD=2,点E为线段PA的靠近点P的三等分点.
(1)求证:PC∥平面BDE;
(2)若异面直线PA与BC所成的角为45°,求多面体BCDEP的体积.
19.在如图所示的几何体中,四边形ABCD是菱形,∠BAD=120°,AE⊥平面ABCD,AE∥CF.
(1)求证:DF∥平面ABE;
(2)若AD=AE=2CF=2,求该几何体的表面积.
20.如图,P为圆锥的顶点,O是圆锥底面的圆心,AC,BD为圆锥底面的两条直径,M为母线PD上一点,连接MA,MO,MC.
(1)若M为PD的中点,证明:PB∥平面MAC;
(2)若PB∥平面MAC,证明:M为PD的中点.
参考答案
一.选择题
1.C2.A3.D4.B5.D6.A7.D8.B9.C10.D11.D12.B
二.填空题
13.2或6.14.3.15.,16.①②.
三.解答题
17.(1)画出过点P且平行于AC和BD的截面PQRS,如图所示:
该截面PQRS是平行四边形,证明如下:
由AC∥平面PQRS,AC?平面ABC,平面ABC∩平面PQRS=PQ,所以AC∥PQ;
同理,AC∥SR;所以PQ∥SR.
同理,PS∥QR,所以四边形PQRS是平行四边形.
(2)当P为AB的中点时,PQ∥AC,且PQ=AC=4;
PS∥BD,且PS=BD=3;
由AC与BD所成角为60°,所以PS、PQ所成的角也是60°,
所以截面四边形PQRS的面积为
S平行四边形PQRS=PS?PQ?sin60°=3×4×=6.
18.(1)连接AC交BD于点O,连接OE.
因 ABCD是直角梯形,且AD⊥DC,AD∥BC,AD=4,BC=2,
所以△ADO和△CBO相似,且有==2;
又点E为线段PA的靠近点P的三等分点,有=2,
所以有=;
所以OE∥CP.
又OE?平面BDE,
所以PC∥平面BDE.
(2)直线PA与BC所成的角为45°,即∠PAD=45°,
又AD=4,PD⊥平面ABCD,所以PD=AD=4.
计算得V四棱锥P﹣ABCD=×(2+4)×2×4=8,
V三棱锥E﹣ABD=××4×2××4=.
所以多面体BCDEP的体积为V多面体BCDEP=V四棱锥P﹣ABCD﹣V三棱锥E﹣ABD=8﹣=.
19.(1)证明:因为AE∥CF,CF?平面ABE,
所以CF∥平面ABE,
因为四边形ABCD是菱形,
所以CD∥AB,
由于CD?平面ABE,
所以CD∥平面ABE,
又CF∩CD=C,
所以平面CDF∥平面ABE,
又DF?平面CDF,
所以DF∥平面ABE.
(2)由AE∥CF,知A,C,F,E四点共面,
连接AC,于是该几何体是由两个相同的四棱锥B﹣ACFE,D﹣ACFE构成的,
由题意知,S△ABE==2,S△ABC==,S△BCF==1,
在△BEF中,EF=,BE=2,BF=,S△BEF==,
所以该几何体的表面积为2×(S△ABE+S△ABC+S△BCF+S△BEF)=6+2+2.
20.证明:(1)若M为PD的中点,由BD为圆锥底面的直径,有O为BD的中点,
则在△PBD中有MO∥PB,
又MO?平面MAC,PB?平面MAC,
则有PB∥平面MAC.
(2)若PB∥平面MAC,由PB?平面PBD,平面PBD∩平面MAC=MO,
可得PB∥MO,
所以在△PBD中,=,
又O为BD的中点,则有DM=MP,
则M为PD的中点.
同课章节目录
