初中数学人教版八年级上第十二章全等三角形 三角形全等的判定课件(共17张ppt)
文档属性
| 名称 | 初中数学人教版八年级上第十二章全等三角形 三角形全等的判定课件(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 888.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
前面的知识你忘记了吗?
让我们一起来复习一下吧
边角边公理
(3种)
我们学过几种三角形的全等判定呢?
角边角公理
角角边公理
边角边公理(SAS)
有两边和它们的夹角对应相等的两个三角形全等
小结
角边角公理(ASA)
有两个角和它们的夹边对应相等的两个三角形全等
小结
角角边公理(AAS)
有两角和其中一角的对边对应相等的两个三角形全等
小结
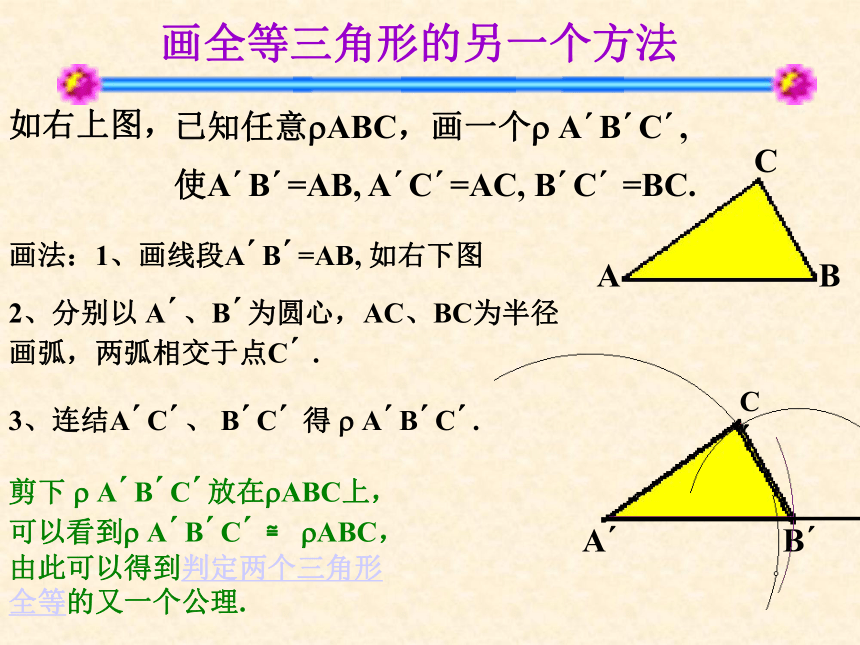
画全等三角形的另一个方法
如右上图,
画法:1、画线段A?B?=AB,
如右下图
2、分别以
A?、B?为圆心,AC、BC为半径画弧,两弧相交于点C?
.
3、连结A?C?、
B?C?
得
?
A?B?C?.
剪下
?
A?B?C?放在?ABC上,可以看到?
A?B?C?
≌
?ABC,由此可以得到判定两个三角形全等的又一个公理.
A
B
C
A?
B?
C?
已知任意?ABC,画一个?
A?B?C?,
使A?B?=AB,
A?C?=AC,
B?C?
=BC.
有三边对应相等的两个三角形全等
学个新知识
边边边(SSS)公理
小结
证明:
AD
=
AD
(公共边),
在?ABD
和?ACD中,
AB
=
AC,
DB
=
DC
(D是中点),
∴
?ABD
≌
?ACD(SSS),
∴
∠1
=
∠BDC
=
(平角定义)
∴∠1=
∠2
(全等三角形的对应角相等).
∴
AD⊥BC(垂直定义)
90°
如图,?ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架。
求证:AD⊥BC
例
1
例
2
已知:如图,AB=DC,AD=BC.
求证:
∠A=
∠C.
提示:要证明∠A=
∠C,可设法使它们分别在两个三角形中,为此,只要连结BD即可
证明:
连结BD
在?BAD
和?DCB中,
AB
=
CD
AD
=
CB
BD
=
DB
(公共边)
∴∠A
=
∠C
(全等三角形的对应角相等).
∴
?BAD
≌
?DCB(SSS),
课堂练习
练习三
练习二
练习一
练
习
三
已知:如右图,AB、CD相交于点O,AC∥DB,OC
=
OD,
E、F为
AB上两点,且AE
=
BF.
求证:CE=DF.
证明:
在?AOC
和?BOD中,
∵
AC∥DB,
∴∠A
=
∠B
(
两直线平等,内错角相等
).
又∵
∠AOC
=
∠BOD(对顶角相等)
∠A
=
∠B
(
已证
),
OC
=
OD(已知)
∴
?AOC
≌
?BOD(AAS)
∴
AC
=
BD
在?AEC
和?BFD中,
AC
=
BD(已证),
∠A
=
∠B
(
已证
),
AE
=
BF(已知).
∴
?AEC
≌
?BFD(ASA)
∴
CE
=
DF
练
习
二
已知:AB=AD,CB=CD.
求证:AC⊥BD.
分析:欲证AC⊥BD,只需证∠AOB=
∠AOD,这就要证明
?ABO
≌
?ADO,它已经具备了两个条件:
AB=AD,OA=AO,所以只需证∠BAO=
∠DAO,为了证明这一点,还需证明?ABC
≌
?ADC.
证明:
在?ABC
和?ADC中,
AB
=
AD
(已知),
CB
=
CD(已知),
AC
=
AC
(公共边)
∴
?ABC
≌
?ADC(SSS),
∴
∠BAO
=
∠DAO
(全等三角形的对应角相等)
在?ABO
和?ADO中,
AB
=
AD
(已知),
∠BAO
=
∠DAO
(已证),
AO=
AO
(公共边)
∴
?ABO
≌
?ADO(SAS),
∴
∠AOB
=
∠AOD
(全等三角形的对应角相等)
∴
∠AOB
=
∠AOD=
90°.
∴AC⊥BD(垂直定义).
又∵∠AOB
+
∠AOD
=180°(邻补角定义)
如右图,
已知:?ABC的顶点和?
DBC的顶点A和D在BC的同旁,
AB
=DC,
AC
=
DB,
AC和DB相交于点O.
求证:OA
=OD.
练习一
证明:
在?ABC和?DCB中,
∴∠A
=
∠D
(全等三角形的对应角相等).
AB
=DC(已知),
AC
=
DB
(已知),
BC
=
CB
(公共边),
∴
?ABC
≌
?DCB(SSS)
在?AOB
和?DOC中,
∠AOB
=
∠DOC
(对顶角)
∠A
=
∠D
(已证)
AB
=DC
(已知)
∴
?AOB
≌
?DOC(AAS)
∴
OA
=OD.
再接再厉,让我们继续学习新知识吧
边角边公理
角边角公理
角角边公理
课
堂
小
结
边边边公理
前面的知识你忘记了吗?
让我们一起来复习一下吧
边角边公理
(3种)
我们学过几种三角形的全等判定呢?
角边角公理
角角边公理
边角边公理(SAS)
有两边和它们的夹角对应相等的两个三角形全等
小结
角边角公理(ASA)
有两个角和它们的夹边对应相等的两个三角形全等
小结
角角边公理(AAS)
有两角和其中一角的对边对应相等的两个三角形全等
小结
画全等三角形的另一个方法
如右上图,
画法:1、画线段A?B?=AB,
如右下图
2、分别以
A?、B?为圆心,AC、BC为半径画弧,两弧相交于点C?
.
3、连结A?C?、
B?C?
得
?
A?B?C?.
剪下
?
A?B?C?放在?ABC上,可以看到?
A?B?C?
≌
?ABC,由此可以得到判定两个三角形全等的又一个公理.
A
B
C
A?
B?
C?
已知任意?ABC,画一个?
A?B?C?,
使A?B?=AB,
A?C?=AC,
B?C?
=BC.
有三边对应相等的两个三角形全等
学个新知识
边边边(SSS)公理
小结
证明:
AD
=
AD
(公共边),
在?ABD
和?ACD中,
AB
=
AC,
DB
=
DC
(D是中点),
∴
?ABD
≌
?ACD(SSS),
∴
∠1
=
∠BDC
=
(平角定义)
∴∠1=
∠2
(全等三角形的对应角相等).
∴
AD⊥BC(垂直定义)
90°
如图,?ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架。
求证:AD⊥BC
例
1
例
2
已知:如图,AB=DC,AD=BC.
求证:
∠A=
∠C.
提示:要证明∠A=
∠C,可设法使它们分别在两个三角形中,为此,只要连结BD即可
证明:
连结BD
在?BAD
和?DCB中,
AB
=
CD
AD
=
CB
BD
=
DB
(公共边)
∴∠A
=
∠C
(全等三角形的对应角相等).
∴
?BAD
≌
?DCB(SSS),
课堂练习
练习三
练习二
练习一
练
习
三
已知:如右图,AB、CD相交于点O,AC∥DB,OC
=
OD,
E、F为
AB上两点,且AE
=
BF.
求证:CE=DF.
证明:
在?AOC
和?BOD中,
∵
AC∥DB,
∴∠A
=
∠B
(
两直线平等,内错角相等
).
又∵
∠AOC
=
∠BOD(对顶角相等)
∠A
=
∠B
(
已证
),
OC
=
OD(已知)
∴
?AOC
≌
?BOD(AAS)
∴
AC
=
BD
在?AEC
和?BFD中,
AC
=
BD(已证),
∠A
=
∠B
(
已证
),
AE
=
BF(已知).
∴
?AEC
≌
?BFD(ASA)
∴
CE
=
DF
练
习
二
已知:AB=AD,CB=CD.
求证:AC⊥BD.
分析:欲证AC⊥BD,只需证∠AOB=
∠AOD,这就要证明
?ABO
≌
?ADO,它已经具备了两个条件:
AB=AD,OA=AO,所以只需证∠BAO=
∠DAO,为了证明这一点,还需证明?ABC
≌
?ADC.
证明:
在?ABC
和?ADC中,
AB
=
AD
(已知),
CB
=
CD(已知),
AC
=
AC
(公共边)
∴
?ABC
≌
?ADC(SSS),
∴
∠BAO
=
∠DAO
(全等三角形的对应角相等)
在?ABO
和?ADO中,
AB
=
AD
(已知),
∠BAO
=
∠DAO
(已证),
AO=
AO
(公共边)
∴
?ABO
≌
?ADO(SAS),
∴
∠AOB
=
∠AOD
(全等三角形的对应角相等)
∴
∠AOB
=
∠AOD=
90°.
∴AC⊥BD(垂直定义).
又∵∠AOB
+
∠AOD
=180°(邻补角定义)
如右图,
已知:?ABC的顶点和?
DBC的顶点A和D在BC的同旁,
AB
=DC,
AC
=
DB,
AC和DB相交于点O.
求证:OA
=OD.
练习一
证明:
在?ABC和?DCB中,
∴∠A
=
∠D
(全等三角形的对应角相等).
AB
=DC(已知),
AC
=
DB
(已知),
BC
=
CB
(公共边),
∴
?ABC
≌
?DCB(SSS)
在?AOB
和?DOC中,
∠AOB
=
∠DOC
(对顶角)
∠A
=
∠D
(已证)
AB
=DC
(已知)
∴
?AOB
≌
?DOC(AAS)
∴
OA
=OD.
再接再厉,让我们继续学习新知识吧
边角边公理
角边角公理
角角边公理
课
堂
小
结
边边边公理
