2020—2021学年八年级数学人教版下册18.1平行四边形复习课(共12张ppt)
文档属性
| 名称 | 2020—2021学年八年级数学人教版下册18.1平行四边形复习课(共12张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 197.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 21:16:43 | ||
图片预览


文档简介
(共12张PPT)
《平行四边形》复习
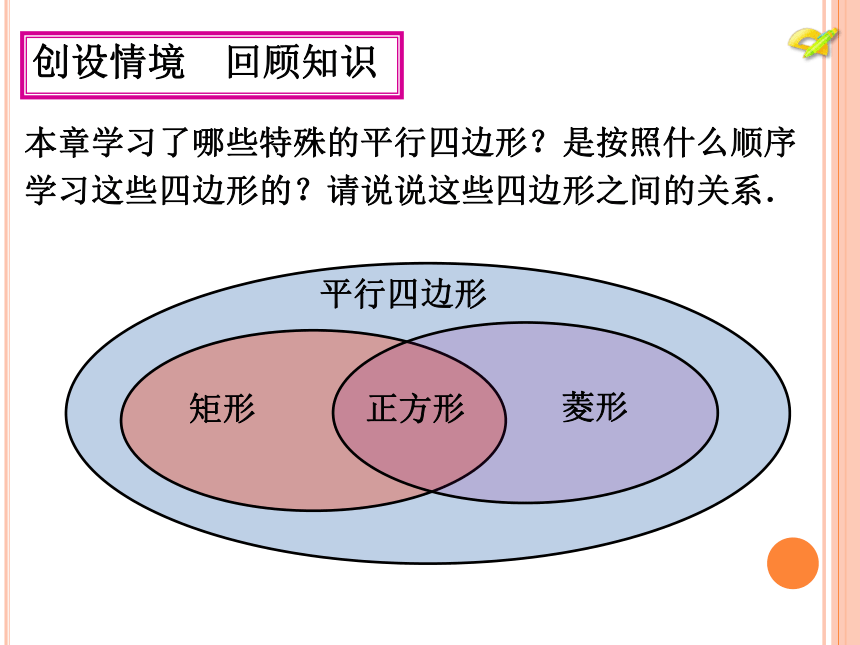
本章学习了哪些特殊的平行四边形?是按照什么顺序
学习这些四边形的?请说说这些四边形之间的关系.
创设情境 回顾知识
矩形
菱形
正方形
平行四边形
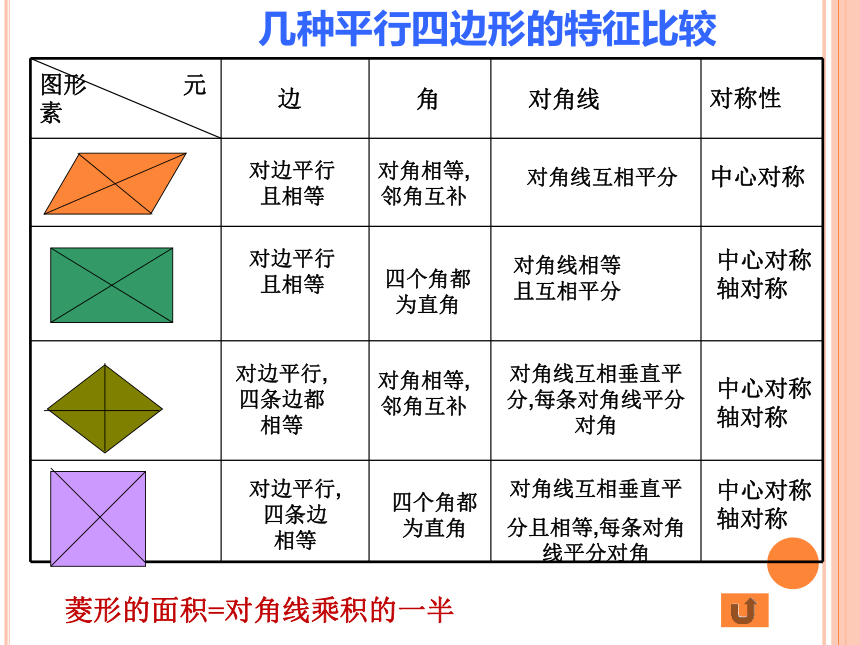
几种平行四边形的特征比较
图形
元素
边
角
对角线
对称性
对边平行
且相等
对边平行
且相等
对边平行,
四条边都
相等
对边平行,
四条边
相等
对角相等,
邻角互补
四个角都
为直角
对角相等,
邻角互补
四个角都
为直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平
分,每条对角线平分
对角
对角线互相垂直平
分且相等,每条对角线平分对角
中心对称
中心对称
轴对称
中心对称
轴对称
中心对称
轴对称
菱形的面积=对角线乘积的一半
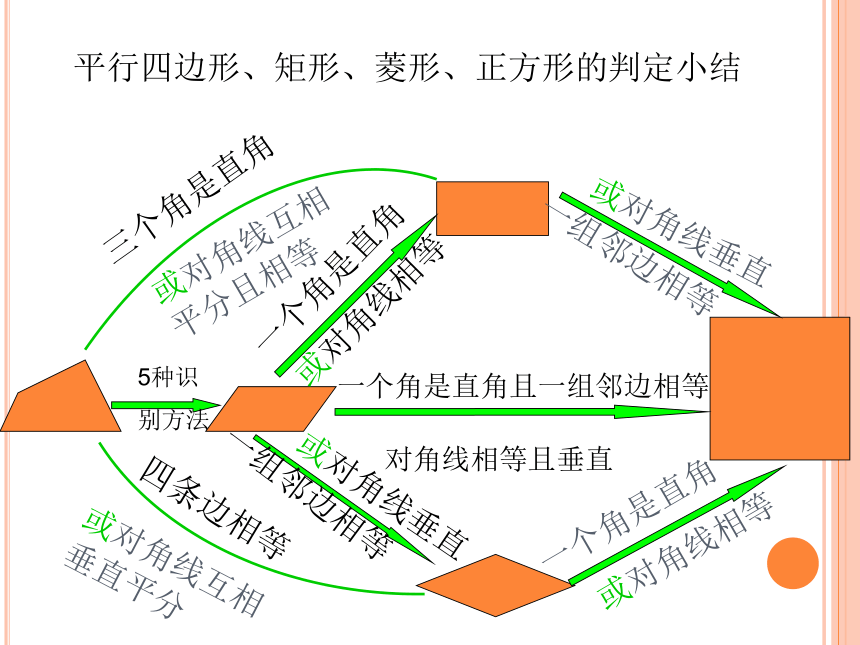
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
或对角线互相平分且相等
或对角线互相垂直平分
对角线相等且垂直
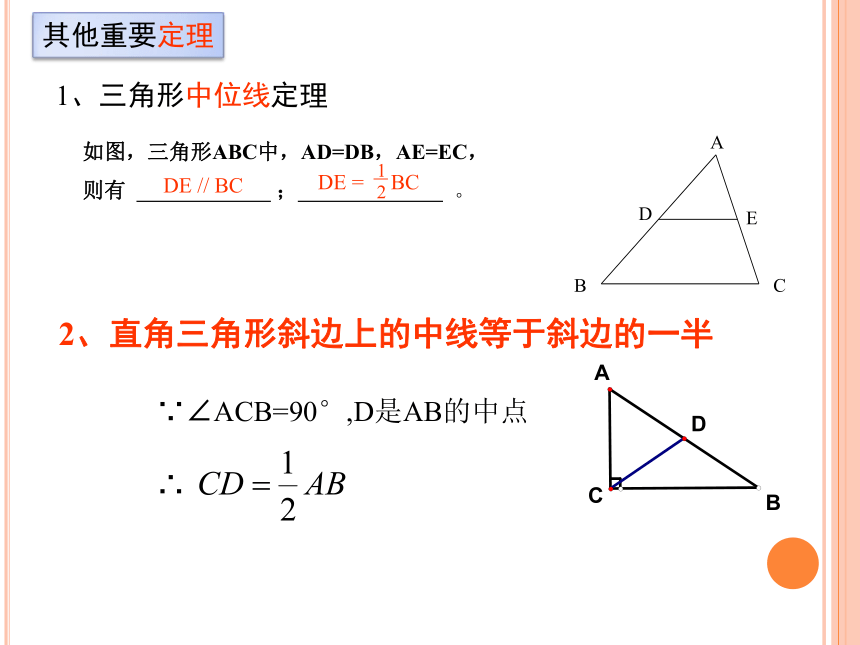
其他重要定理
1、三角形中位线定理
如图,三角形ABC中,AD=DB,AE=EC,
则有
;
。
DE
//
BC
DE
=
BC
1
2
A
B
C
D
E
2、直角三角形斜边上的中线等于斜边的一半
∵∠ACB=90°,D是AB的中点
∴
同步练习
1.如图,已知:AD∥BC,要使四边形ABCD为平行四边形,需要增加条件是______________
2.分析一下命题
,其中是真命题的是____________
(1)一组对边平行,另一组对边相等的四边形是平行四边形。
(2)对角线相等且平分的四边形是矩形;
(3)对角线相等且互相垂直的四边形是正方形;
(4)对角线互相垂直的四边形是平行四边形;
(5)有三个角是直角且邻边相等的四边形是正方形;
(6)有一组邻边相等且对角线互相平分的四边形是菱形;
(7)有一个角是直角的菱形是正方形;
(8)四条边都相等的四边形是正方形。
AD=BC(AB
∥CD,
∠A=
∠C,
∠B=
∠D)
2、5、6、7
4.矩形对角线的交角为60°,一条对角线与
较短边的和为18cm,
则对角线长是________。
3.
ABCD的对角线AC与BD交于O,
若S
ABCD=12cm?,
S△AOB=_______。
5.菱形的对角线长为6和8,则周长为_________。
3cm?
12
cm
20
同步练习
6.如图,在正方形ABCD的外侧,作等边三角形CDE,
则∠AEC=________
A
B
C
D
E
45o
1.如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且
DP=OC,连结CP,试判断四边形CODP的形状.
A
B
D
C
O
P
如果题目中的矩形变为菱形以及正方形,结论应变为什么?
例题分析
2.以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC等于
时,四边形ADFE是矩形;
(2)当∠BAC等于
时,平行四边形ADFE不存在;
(3)当△ABC分别满足什么条件时,平行四边形是菱形、正方形.
B
C
A
E
F
D
解:(3)
AB=AC时,平行四边形ADFE时菱形。
AB=AC且∠BAC=150°时,平行四边形ADFE是正方形。
150°
60°
60°
60°
3.如图,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,请判断四边形EFGH的形状,并说明理由。
(1)添加条件_______,则四边形EFGH为菱形;
(2)添加条件_______,则四边形EFGH为矩形;
(3)添加条件_______________,则四边形EFGH为正方形。
O
AC=BD
AC⊥BD
AC⊥BD且AC=BD
通过这节课的复习,
你又增加了哪些收获?
能与大家一起分享吗?
丰
收
园
本课主要知识点
2.特殊四边形的常用判定方法
平行
四边形
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(4)对角线互相平分的四边形是平行四边形;
(5)一组对边平行且相等的四边形是平行四边形。
矩
形
(1)有一个角是直角的平行四边形是矩形;
菱
形
正方形
(3)两组对角分别相等的四边形是平行四边形;
(2)有三个角是直角的四边形是矩形;
(3)对角线相等的平行四边形是矩形。
(1)有一组邻边相等的平行四边形是菱形;
(2)四条边都相等的四边形是菱形;
(3)对角线互相垂直的平行四边形是菱形。
(2)有一组邻边相等的矩形是正方形;
(3)有一个角是直角的菱形是正方形。
(1)有一个角是直角且有一组邻边相等的平行四边形是正方形;
《平行四边形》复习
本章学习了哪些特殊的平行四边形?是按照什么顺序
学习这些四边形的?请说说这些四边形之间的关系.
创设情境 回顾知识
矩形
菱形
正方形
平行四边形
几种平行四边形的特征比较
图形
元素
边
角
对角线
对称性
对边平行
且相等
对边平行
且相等
对边平行,
四条边都
相等
对边平行,
四条边
相等
对角相等,
邻角互补
四个角都
为直角
对角相等,
邻角互补
四个角都
为直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平
分,每条对角线平分
对角
对角线互相垂直平
分且相等,每条对角线平分对角
中心对称
中心对称
轴对称
中心对称
轴对称
中心对称
轴对称
菱形的面积=对角线乘积的一半
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
或对角线互相平分且相等
或对角线互相垂直平分
对角线相等且垂直
其他重要定理
1、三角形中位线定理
如图,三角形ABC中,AD=DB,AE=EC,
则有
;
。
DE
//
BC
DE
=
BC
1
2
A
B
C
D
E
2、直角三角形斜边上的中线等于斜边的一半
∵∠ACB=90°,D是AB的中点
∴
同步练习
1.如图,已知:AD∥BC,要使四边形ABCD为平行四边形,需要增加条件是______________
2.分析一下命题
,其中是真命题的是____________
(1)一组对边平行,另一组对边相等的四边形是平行四边形。
(2)对角线相等且平分的四边形是矩形;
(3)对角线相等且互相垂直的四边形是正方形;
(4)对角线互相垂直的四边形是平行四边形;
(5)有三个角是直角且邻边相等的四边形是正方形;
(6)有一组邻边相等且对角线互相平分的四边形是菱形;
(7)有一个角是直角的菱形是正方形;
(8)四条边都相等的四边形是正方形。
AD=BC(AB
∥CD,
∠A=
∠C,
∠B=
∠D)
2、5、6、7
4.矩形对角线的交角为60°,一条对角线与
较短边的和为18cm,
则对角线长是________。
3.
ABCD的对角线AC与BD交于O,
若S
ABCD=12cm?,
S△AOB=_______。
5.菱形的对角线长为6和8,则周长为_________。
3cm?
12
cm
20
同步练习
6.如图,在正方形ABCD的外侧,作等边三角形CDE,
则∠AEC=________
A
B
C
D
E
45o
1.如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且
DP=OC,连结CP,试判断四边形CODP的形状.
A
B
D
C
O
P
如果题目中的矩形变为菱形以及正方形,结论应变为什么?
例题分析
2.以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.
(1)当∠BAC等于
时,四边形ADFE是矩形;
(2)当∠BAC等于
时,平行四边形ADFE不存在;
(3)当△ABC分别满足什么条件时,平行四边形是菱形、正方形.
B
C
A
E
F
D
解:(3)
AB=AC时,平行四边形ADFE时菱形。
AB=AC且∠BAC=150°时,平行四边形ADFE是正方形。
150°
60°
60°
60°
3.如图,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,请判断四边形EFGH的形状,并说明理由。
(1)添加条件_______,则四边形EFGH为菱形;
(2)添加条件_______,则四边形EFGH为矩形;
(3)添加条件_______________,则四边形EFGH为正方形。
O
AC=BD
AC⊥BD
AC⊥BD且AC=BD
通过这节课的复习,
你又增加了哪些收获?
能与大家一起分享吗?
丰
收
园
本课主要知识点
2.特殊四边形的常用判定方法
平行
四边形
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(4)对角线互相平分的四边形是平行四边形;
(5)一组对边平行且相等的四边形是平行四边形。
矩
形
(1)有一个角是直角的平行四边形是矩形;
菱
形
正方形
(3)两组对角分别相等的四边形是平行四边形;
(2)有三个角是直角的四边形是矩形;
(3)对角线相等的平行四边形是矩形。
(1)有一组邻边相等的平行四边形是菱形;
(2)四条边都相等的四边形是菱形;
(3)对角线互相垂直的平行四边形是菱形。
(2)有一组邻边相等的矩形是正方形;
(3)有一个角是直角的菱形是正方形。
(1)有一个角是直角且有一组邻边相等的平行四边形是正方形;
