2020-2021学年七年级数学苏科版下册-9.5 多项式的因式分解-课件(共32张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册-9.5 多项式的因式分解-课件(共32张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 949.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 20:53:28 | ||
图片预览








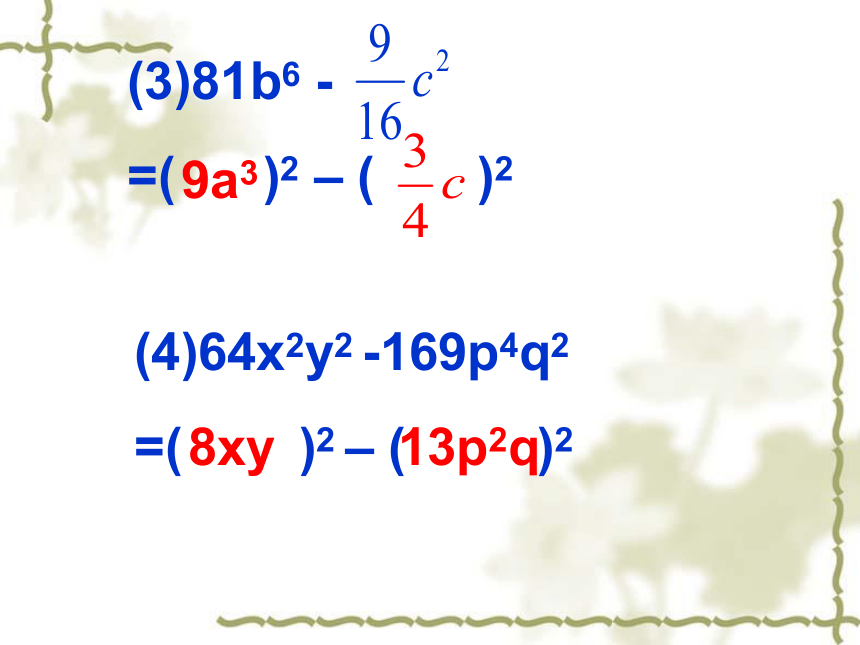

文档简介
(共32张PPT)
9.5
多项式的因式分解(2)
──
公式法
平方差公式
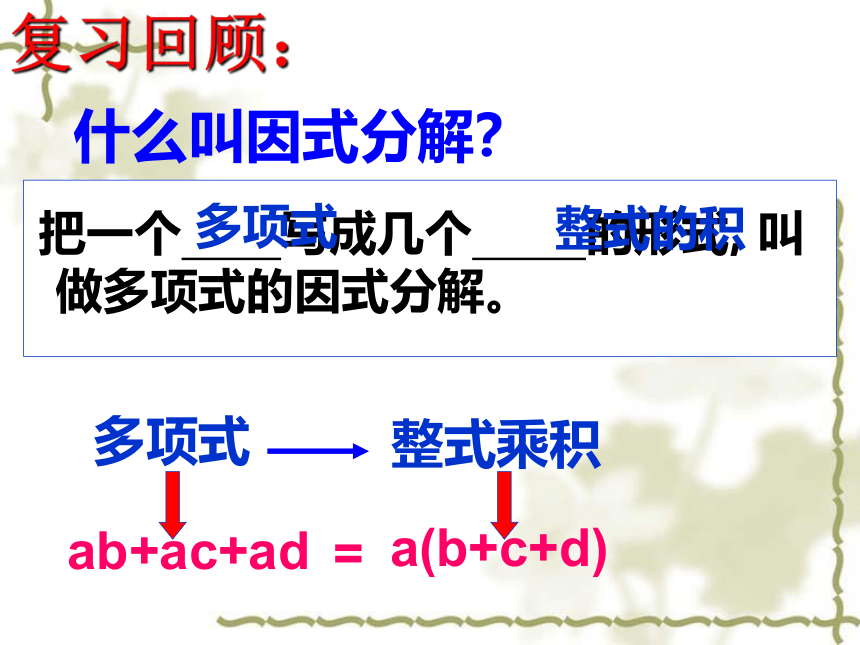
把一个
写成几个
的形式,
叫做多项式的因式分解。
复习回顾:
什么叫因式分解?
多项式
整式乘积
ab+ac+ad
=
a(b+c+d)
多项式
整式的积
计算:
(a+2)(a-2)
=_____________.
(2)
(-4s+t)(t+4s)
=_____________.
(3)
(3a+2b)(3a-2b)
=___________.
a2-4
t2-16s2
9a2-4b2
温故知新
平方差公式
(a+b)(a-b)
=a2-b2
2.
根据上面的算式填空:
(1)
a2-4
=_________________.
(2)
t2-16s2
=____________
.
(3)
9a2-4b2
=________________.
(a+2)(a-2)
(t+4s)(t-4s)
(3a+2b)(3a-2b)
a2-b2
=
(a+b)(a-b)
(1)
a2-4
=_________________.
(2)t2-16s2
=____________.
(3)9a2-4b2
=________________.
(a+2)(a-2)
(t+4s)(t-4s)
(3a+2b)(3a-2b)
因式分解
a2-b2
=
(a+b)(a-b)
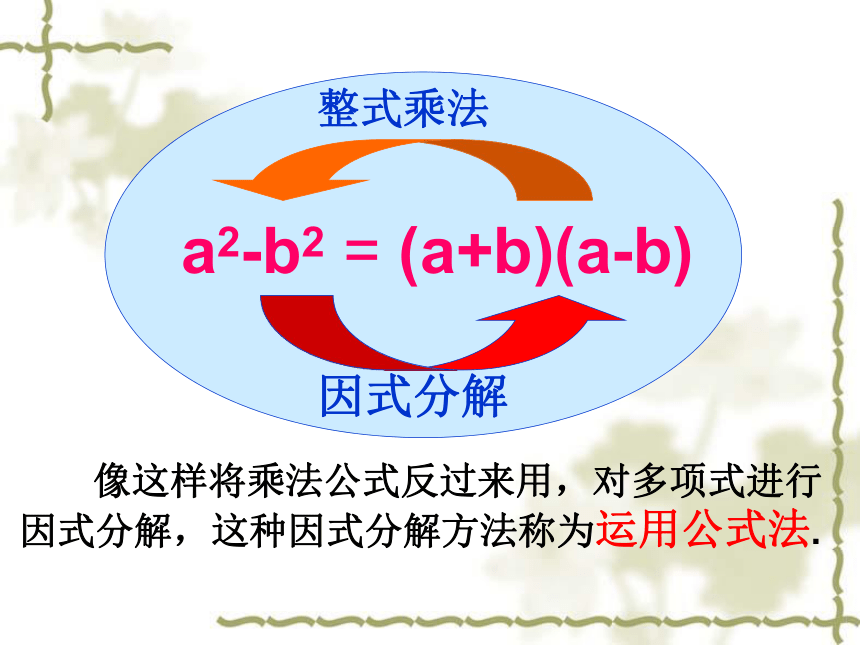
整式乘法
因式分解
像这样将乘法公式反过来用,对多项式进行
因式分解,这种因式分解方法称为运用公式法.
平方差公式
(1)公式:
a2-b2
=
(a+b)(a-b)
(2)语言表述:
两个数的平方差,等于这两个数的和与这两个数的差的积。
平方差公式
(1)公式:
a2-b2
=
(a+b)(a-b)
(3)公式特点:
左边多项式结构特征:
②符号一正一负
③(
)2-(
)2
①只有两项
平方差公式
(1)公式:
a2-b2
=
(a+b)(a-b)
(4)模板结构:
●2-△2=(●+△)(●-△)
牛刀小试
(1)x2+y2
(2)-x2+y2
(3)-x2-y2
(4)x2-(-y)2
×
√
√
×
练习1:下列多项式可否用平方差
公式进行分解因式?
(5)2a2-b2
(6)9m2-
4n
×
×
牛刀小试
练习2:
(1)
4x2
-25m2
=(
)2
-
(
)2
(2)36a4
-0.49b2
=(
)2
–(
)2
0.7b
5m
6a2
2x
(3)81b6
-
=(
)2
–
(
)2
(4)64x2y2
-169p4q2
=(
)2
–
(
)2
8xy
9a3
13p2q
请每位同学写出两个能运用平方
差公式分解因式的多项式
牛刀小试
用平方差公式分解因式
x2
-
y2
=(
+
)(
-
)
x
x
y
y
x
y
x
y
用平方差公式分解因式
x2
-
9
=(
+
)(
-
)
x
x
x
x
y
y2
=x2
-
32
3
3
y
(
)2-(
)2
用平方差公式分解因式
x2
-
9
=(
+
)(
-
)
x
x
x
x
=x2
-
32
3
3
y2
(3y)2
3y
3y
用平方差公式分解因式
x2
-
9
=(
+
)(
-
)
x
x
x
x
=
x2
-
3y
3y
y2
4
=(
)2
–(
)2
2x
3y
2x
(3y)2
=(
+
)(
-
)
3y
3y
2x
牛刀小试
请把自己写的多项式交给同桌,并请同桌写出完整的分解因式过程
趁热打铁
1、把下列各式分解因式:
(1)m2-
(2)9x2-4y2
(3)-c2+a2b2
16
(
)2-(
)2
x+m
x+n
x+m
x+m
x+n
x+n
+
-
(
)
(
)
(
)
=[
]
[
]
(
)
=(
)(
)
x+m+x+n
x+m-x-n
=(
)(
)
2x+m+n
m-n
公式中的
a、b既可以是单独
的数字、
字母,也
可以是单
项式、多
项式。
x4
-16
x2
-
y2
=(x2)2-42
=(
)(
)
x2
+
4
x2
-
4
22
=(
)(
)(
)
x2
+
4
x+2
x-2
各因式分解到不能再分解为止.
2、把下列各式分解因式:
(1)(x+p)2-(x+q)2
(2)16(m-n)2-9(m+n)2
趁热打铁
归纳:
(1)
还原成平方差的形式.
(2)
运用公式写成两数和与两数差的积的形式.
(3)
分别在括号内合并同类项.
(4)
各因式分解到不能再分解为止.
运用平方差公式因式分解的一般步骤:
运用平方差公式因式分解的注意点:
1、运用平方差公式分解因式的关键是要把分解的多项式看成两个数的平方差,尤其当系数是分数或小数时,要正确化为两数的平方差。
2、公式a2-b2=(a+b)(a-b)中的字母a,b可以是数,也可以是单项式或多项式,要注意“整体”思想的运用。
3、当要分解的多项式是两个多项式的平方时,分解成的两个
因式要进行去括号化简,若有同类项,要进行合并,直到每个
因式分解到不能再分解为止。
=1000
(m2)
=
(35+15)(35-15)
=
(352-152)
解:
352
-152
如右图,求圆环形绿化区的面积。
35m
15m
答:这个绿化区的面积是1000
m2。
=50×20
用平方差公式分解因式解决计算
因式分解与整式的乘法是互逆的运算,感受数学知识之间的联系。
运用平方差公式分解因式时,要注意步骤与注意点。
知识应用
把下列各式分解因式:
(1)a5-a3
(2)-16+x4y4
(3)27x3-3x(x+1)2
当多项式的各项有公因式时,通常先提出这个公因式,然后再考虑用平方差公式进行因式分解
课堂小测
补充习题P47-48
第1、2、3、4题
智力冲浪:
1、把
(a+b)(a-b)-2(a2-5b2)
分解因式.
2、58-1能被20~30之间的两个整数整除,这两个数是(
)
A、22、24
B、24、26
C、26、28
D、25、27
B
把下列各式分解因式:
(1).
1-x2
(2).
X2-9y2
(3).
4x2-25
(4).
x2y2-z2
(5).
(X+2)2-9
(6).
(x+a)2_
(y-b)2
=(1+x)(1-x)
=(x+3y)(x-3y)
=(2x+5)(2x-5)
=(xy+z)(xy-z)
=(x+5)(x-1)
=[(x+a)+(y-b)]
[(x+a)-(y-b)]
=
(x+a+y-b)
(x+a-y+b)
平方差公式
(1)公式:
a2-b2
=
(a+b)(a-b)
(2)语言表述:
两个数的平方差,等于这两个数的和与这两个数的差的积。
(3)公式特点:
左边结构特征:
②符号一正一负
③(
)2-(
)2
①只有两项
(4)模板结构:
●2-△2=(●+△)(●-△)
(2)16(m-n)2-9(m+n)2
原式=[4(m-n)]2-[3(m+n)]2
(1)还原成平方差的形式.
=[4(m-n)+3(m+n)][4(m-n)-3(m+n)]
(2)运用公式写成两数和与
两数差的积的形式.
=(4m-4n+3m+3n)(4m-4n-3m-3n)
=(7m-n)(m-7n)
(3)
分别在括号内合并同类项.
(1)a5-a3
(4)各因式分解到不能再分解为止.
9.5
多项式的因式分解(2)
──
公式法
平方差公式
把一个
写成几个
的形式,
叫做多项式的因式分解。
复习回顾:
什么叫因式分解?
多项式
整式乘积
ab+ac+ad
=
a(b+c+d)
多项式
整式的积
计算:
(a+2)(a-2)
=_____________.
(2)
(-4s+t)(t+4s)
=_____________.
(3)
(3a+2b)(3a-2b)
=___________.
a2-4
t2-16s2
9a2-4b2
温故知新
平方差公式
(a+b)(a-b)
=a2-b2
2.
根据上面的算式填空:
(1)
a2-4
=_________________.
(2)
t2-16s2
=____________
.
(3)
9a2-4b2
=________________.
(a+2)(a-2)
(t+4s)(t-4s)
(3a+2b)(3a-2b)
a2-b2
=
(a+b)(a-b)
(1)
a2-4
=_________________.
(2)t2-16s2
=____________.
(3)9a2-4b2
=________________.
(a+2)(a-2)
(t+4s)(t-4s)
(3a+2b)(3a-2b)
因式分解
a2-b2
=
(a+b)(a-b)
整式乘法
因式分解
像这样将乘法公式反过来用,对多项式进行
因式分解,这种因式分解方法称为运用公式法.
平方差公式
(1)公式:
a2-b2
=
(a+b)(a-b)
(2)语言表述:
两个数的平方差,等于这两个数的和与这两个数的差的积。
平方差公式
(1)公式:
a2-b2
=
(a+b)(a-b)
(3)公式特点:
左边多项式结构特征:
②符号一正一负
③(
)2-(
)2
①只有两项
平方差公式
(1)公式:
a2-b2
=
(a+b)(a-b)
(4)模板结构:
●2-△2=(●+△)(●-△)
牛刀小试
(1)x2+y2
(2)-x2+y2
(3)-x2-y2
(4)x2-(-y)2
×
√
√
×
练习1:下列多项式可否用平方差
公式进行分解因式?
(5)2a2-b2
(6)9m2-
4n
×
×
牛刀小试
练习2:
(1)
4x2
-25m2
=(
)2
-
(
)2
(2)36a4
-0.49b2
=(
)2
–(
)2
0.7b
5m
6a2
2x
(3)81b6
-
=(
)2
–
(
)2
(4)64x2y2
-169p4q2
=(
)2
–
(
)2
8xy
9a3
13p2q
请每位同学写出两个能运用平方
差公式分解因式的多项式
牛刀小试
用平方差公式分解因式
x2
-
y2
=(
+
)(
-
)
x
x
y
y
x
y
x
y
用平方差公式分解因式
x2
-
9
=(
+
)(
-
)
x
x
x
x
y
y2
=x2
-
32
3
3
y
(
)2-(
)2
用平方差公式分解因式
x2
-
9
=(
+
)(
-
)
x
x
x
x
=x2
-
32
3
3
y2
(3y)2
3y
3y
用平方差公式分解因式
x2
-
9
=(
+
)(
-
)
x
x
x
x
=
x2
-
3y
3y
y2
4
=(
)2
–(
)2
2x
3y
2x
(3y)2
=(
+
)(
-
)
3y
3y
2x
牛刀小试
请把自己写的多项式交给同桌,并请同桌写出完整的分解因式过程
趁热打铁
1、把下列各式分解因式:
(1)m2-
(2)9x2-4y2
(3)-c2+a2b2
16
(
)2-(
)2
x+m
x+n
x+m
x+m
x+n
x+n
+
-
(
)
(
)
(
)
=[
]
[
]
(
)
=(
)(
)
x+m+x+n
x+m-x-n
=(
)(
)
2x+m+n
m-n
公式中的
a、b既可以是单独
的数字、
字母,也
可以是单
项式、多
项式。
x4
-16
x2
-
y2
=(x2)2-42
=(
)(
)
x2
+
4
x2
-
4
22
=(
)(
)(
)
x2
+
4
x+2
x-2
各因式分解到不能再分解为止.
2、把下列各式分解因式:
(1)(x+p)2-(x+q)2
(2)16(m-n)2-9(m+n)2
趁热打铁
归纳:
(1)
还原成平方差的形式.
(2)
运用公式写成两数和与两数差的积的形式.
(3)
分别在括号内合并同类项.
(4)
各因式分解到不能再分解为止.
运用平方差公式因式分解的一般步骤:
运用平方差公式因式分解的注意点:
1、运用平方差公式分解因式的关键是要把分解的多项式看成两个数的平方差,尤其当系数是分数或小数时,要正确化为两数的平方差。
2、公式a2-b2=(a+b)(a-b)中的字母a,b可以是数,也可以是单项式或多项式,要注意“整体”思想的运用。
3、当要分解的多项式是两个多项式的平方时,分解成的两个
因式要进行去括号化简,若有同类项,要进行合并,直到每个
因式分解到不能再分解为止。
=1000
(m2)
=
(35+15)(35-15)
=
(352-152)
解:
352
-152
如右图,求圆环形绿化区的面积。
35m
15m
答:这个绿化区的面积是1000
m2。
=50×20
用平方差公式分解因式解决计算
因式分解与整式的乘法是互逆的运算,感受数学知识之间的联系。
运用平方差公式分解因式时,要注意步骤与注意点。
知识应用
把下列各式分解因式:
(1)a5-a3
(2)-16+x4y4
(3)27x3-3x(x+1)2
当多项式的各项有公因式时,通常先提出这个公因式,然后再考虑用平方差公式进行因式分解
课堂小测
补充习题P47-48
第1、2、3、4题
智力冲浪:
1、把
(a+b)(a-b)-2(a2-5b2)
分解因式.
2、58-1能被20~30之间的两个整数整除,这两个数是(
)
A、22、24
B、24、26
C、26、28
D、25、27
B
把下列各式分解因式:
(1).
1-x2
(2).
X2-9y2
(3).
4x2-25
(4).
x2y2-z2
(5).
(X+2)2-9
(6).
(x+a)2_
(y-b)2
=(1+x)(1-x)
=(x+3y)(x-3y)
=(2x+5)(2x-5)
=(xy+z)(xy-z)
=(x+5)(x-1)
=[(x+a)+(y-b)]
[(x+a)-(y-b)]
=
(x+a+y-b)
(x+a-y+b)
平方差公式
(1)公式:
a2-b2
=
(a+b)(a-b)
(2)语言表述:
两个数的平方差,等于这两个数的和与这两个数的差的积。
(3)公式特点:
左边结构特征:
②符号一正一负
③(
)2-(
)2
①只有两项
(4)模板结构:
●2-△2=(●+△)(●-△)
(2)16(m-n)2-9(m+n)2
原式=[4(m-n)]2-[3(m+n)]2
(1)还原成平方差的形式.
=[4(m-n)+3(m+n)][4(m-n)-3(m+n)]
(2)运用公式写成两数和与
两数差的积的形式.
=(4m-4n+3m+3n)(4m-4n-3m-3n)
=(7m-n)(m-7n)
(3)
分别在括号内合并同类项.
(1)a5-a3
(4)各因式分解到不能再分解为止.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
