七年级数学(分类讲义)总复习 一元一次方程的应用
文档属性
| 名称 | 七年级数学(分类讲义)总复习 一元一次方程的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 37.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-13 00:00:00 | ||
图片预览




文档简介
一元一次方程的应用
一、列方程解应用题的主要步骤:
1、认真审题,理解题意,弄清题目中的数量关系,找出其中的等量关系;
2、用字母表示题目中的未知数,并用这个字母和已知数一起组成表示各数量关系的代数式;
3、利用这些代数式列出反映某个等量关系的方程(注意所使用的单位一定要统一);
4、求出所列方程的解;
5、检验所求的解是否使方程成立,又能使应用题有意义,并写出答案。
二、对常见应用题的解法分析
1、和、差、倍、分问题;这类问题主要应搞清各量之间的关系,注意关键词语。(1)倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率……”来体现。(2)多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。
例2、旅行社的一辆汽车在第一次旅程中用去油箱里汽油的25%,第二次旅程中用去剩余汽油的40%,这样油箱中剩的汽油比两次所用的汽油少1公斤,求油箱里原有汽油多少公斤?
分析:等量关系为:油箱中剩余汽油+1=用去的汽油。
解:设油箱里原有汽油x公斤,
由题意得,x(1-25%)(1-40%)+1=25%x+(1-25%)x×40%
∴ x=10
答:油箱里原有汽油10公斤。
2、等积变形问题:
“等积变形”是以形状改变而体积不变为前提。常用等量关系为:原料体积=成品体积。
例3、现有直径为0.8米的圆柱形钢坯30米,可足够锻造直径为0.4米,长为3米的圆柱形机轴多少根?
分析:等量关系为:机轴的体积和=钢坯的体积。
解:设可足够锻造x根机轴,
由题意得,π()2×3x=π()2×30
x=×10×==40
答:可足够锻造直径为0.4米,长为3米的圆柱形机轴40根。
3、劳力调配问题:
这类问题要搞清人数的变化,常见题型有(1)既有调入又有调出。(2)只有调入没有调出,调入部分变化,其余不变;(3)只有调出没有调入,调出部分变化,其余不变。
例4、有两个工程队,甲队有285人,乙队有183人,若要求乙队人数是甲队人数的,应从乙队调多少人到甲队?
分析:此问题中对乙队来说有调出,对甲队来说有调入。等量关系为:乙队调出后人数=甲队调入后人数。
解:设应从乙队调x人到甲队,
由题意得,183-x=(285+x)
解这个方程,285+x=549-3x
4x=264
∴ x=66
答:应从乙队调66人到甲队。
例5、甲、乙两个工程队分别有188人和138人,现需要从两队抽出116人组成第三个队,并使甲、乙两队剩余人数之比为2:1,问应从甲、乙两队各抽出多少人?
分析:此问题中只有调出,没有调入。等量关系为:甲队调出后人数=2×乙队调出后人数。
解:设应从甲队抽出x人,则应从乙队抽出(116-x)人,
由题意得,188-x=2[138-(116-x)]
解这个方程188-x=2(138-116+x)
188-x=44+2x
3x=144
∴ x=48
116-x=116-48=68
答:应从甲队抽出48人,从乙队抽出68人。
4、比例分配问题:
这类问题的一般思路为:设其中一份为x ,利用已知的比,写出相应的代数式。
常用等量关系:各部分之和=总量。
例7、甲、乙、丙三个人每天生产机器零件数为甲、乙之比为4:3;乙、丙之比为6:5,又知甲与丙的和比乙的2倍多12件,求每个人每天生产多少件?
分析:应设一份为x件,则其他量均可用含x的代数式表示。等量关系为:(甲日产量+丙日产量)-12=乙日产量的2倍。
解:设一份为x件,则甲每天生产4x件,乙每天生产3x件,丙每天生产×3x件(即x件),
由题意得,4x+x-12=2×3x
解这个方程,=12
∴ x=24
∴ 4x=4×24=96(件),3x=3×24=72(件),x=×24=60(件)
答:甲每天生产96件,乙每天生产72件,丙每天生产60件。
5、数字问题:
要搞清楚数的表示方法:一个三位数的百位数字为a,十位数字是b,个位数字为c(其中a、b、c均为整数,且
1≤a≤9, 0≤b≤9, 0≤c≤9)则这个三位数表示为:100a+10b+c。
例8、一个2位数,个位上的数字比十位上的数学大5,且个位上的数字与十位上的数字的和比这个2位数的大6,求这个2位数。
分析:等量关系为:个位数字+十位数字-6=×这个2位数。
解:设十位上的数字为x,则个位上的数字为x+5,
则这个2位数为:10x+x+5
由题意得,x+5+x-6=(10x+x+5)
∴ x=4
∴ x+5=9
这个2位数为49。
6、工程问题:
工程问题中的三个量及其关系为:工作总量=工作效率×工作时间
经常在题目中未给出工作总量时,设工作总量为单位1。
例9、一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
分析:设工程总量为单位1,等量关系为:甲完成工作量+乙完成工作量=工作总量。
解:设乙还需x天完成全部工程,设工作总量为单位1,
由题意得,(+)×3+=1,
∴ x==6
答:乙还需6天才能完成全部工程。
例10、一个蓄水池有甲、乙两个进水管和一个丙排水管,单独开甲管6小时可注满水池;单位开乙管8小时可注满水池,单独开丙管9小时可将满池水排空,若先将甲、乙管同时开放2小时,然后打开丙管,问打开丙管后几小时可注满水池?
分析:等量关系为:甲注水量+乙注水量-丙排水量=1。
解:设打开丙管后x小时可注满水池,
由题意得,(+)(x+2)-=1
13x=30
∴ x==2
答:打开丙管后2小时可注满水池
真题专练:
1.(河北省)某种收音机,原来每台售价48元,降价后每台售价42元,则降价的百分数为________。
2.(湖南长沙)国家规定储蓄存款需征收利息税,利息税的税率是20%(即储蓄利息的20%)。小红在银行存入人民币二万元,定期一年,年息为432元,存款到期时,应交利息税________元。
3.(江苏南京)有一旅客携带了30公斤行李从南京禄口国际机场乘飞机去天津,按民航规定,旅客最多可免费携带20公斤行李,超重部分每公斤按飞机票价格的1.5%购买行李票,现该旅客购买了120元的行李票,则他的飞机 票价格应是( )
A、1000元 B、800元 C、600元 D、400元
5.(北京西城区)一个角的余角比它的补角的还少20°,求这个角。
6.(吉林省)某初一学生在做作业时,不慎将墨水瓶打翻,使一道作业题只看到如下字样:“甲、乙两地相距40千米,摩托车的速度为45千米/时,运货汽车的速度为35千米/时,〓〓 (涂黑部分表示被墨水覆盖的若干文字)请将这道作业题补充完整,并列方程解答。
8.(安徽省)目前,包括长江、黄河等七大流域在内,全国水土流失面积达到367万平方千米,其中长江与黄河流域的水土流失总面积占全国的32.4%。而长江流域的水土流失问题更为严重,它的水土流失面积比黄河流域的水土流失面积还要多29万平方千米。问长江流域的水土流失面积是多少?(结果保留整数)
7、行程问题:
[解题指导]
(1)行程问题中的三个基本量及其关系: 路程=速度×时间。
(2)基本类型有
1)相遇问题;
2)追及问题;常见的还有:相背而行;行船问题;环形跑道问题。
(3)解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系,一般情况下问题就能迎刃而解。并且还常常借助画草图来分析,理解行程问题。
例11:甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
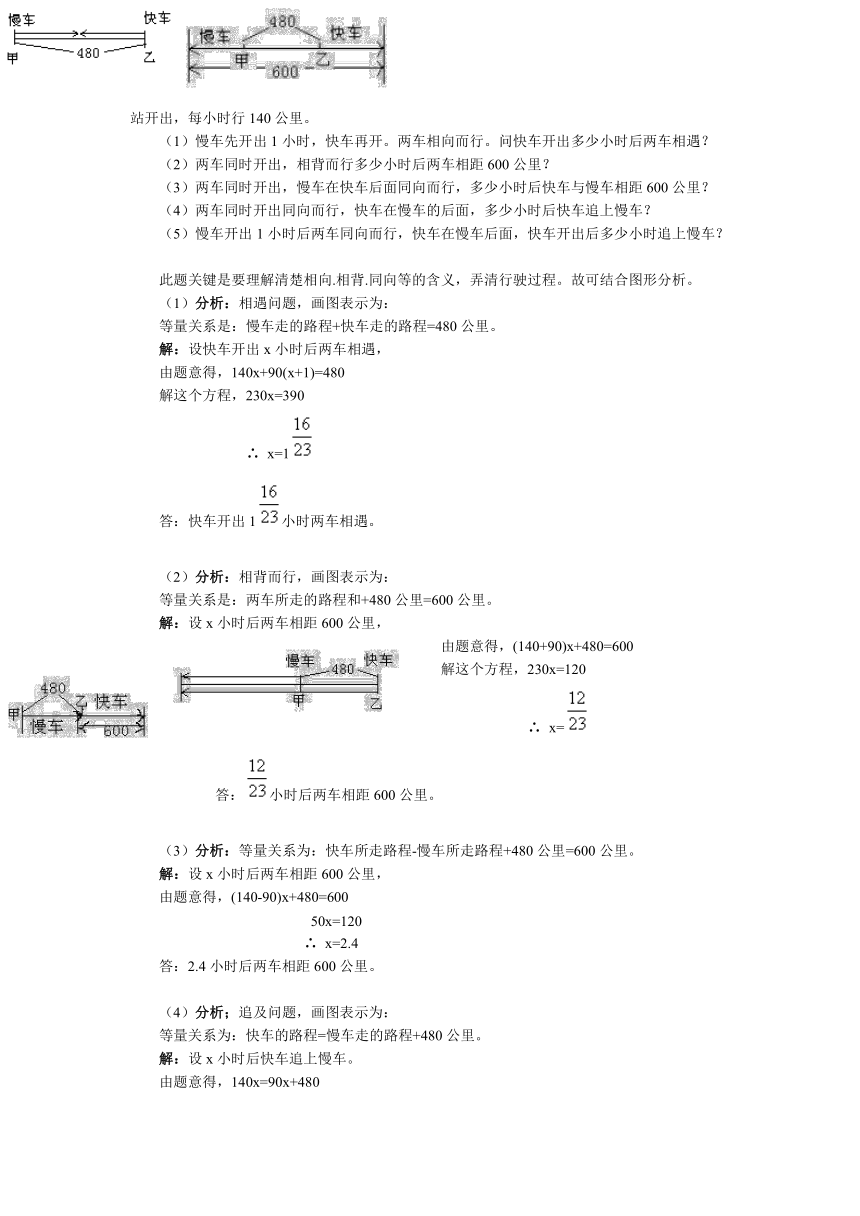
(1)慢车先开出1小时,快车再开。两车相向而行。问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600公里?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里?
(4)两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
(5)慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车?
此题关键是要理解清楚相向.相背.同向等的含义,弄清行驶过程。故可结合图形分析。
(1)分析:相遇问题,画图表示为:
等量关系是:慢车走的路程+快车走的路程=480公里。
解:设快车开出x小时后两车相遇,
由题意得,140x+90(x+1)=480
解这个方程,230x=390
∴ x=1
答:快车开出1小时两车相遇。
(2)分析:相背而行,画图表示为:
等量关系是:两车所走的路程和+480公里=600公里。
解:设x小时后两车相距600公里,
由题意得,(140+90)x+480=600
解这个方程,230x=120
∴ x=
答:小时后两车相距600公里。
(3)分析:等量关系为:快车所走路程-慢车所走路程+480公里=600公里。
解:设x小时后两车相距600公里,
由题意得,(140-90)x+480=600
50x=120
∴ x=2.4
答:2.4小时后两车相距600公里。
(4)分析;追及问题,画图表示为:
等量关系为:快车的路程=慢车走的路程+480公里。
解:设x小时后快车追上慢车。
由题意得,140x=90x+480
解这个方程,50x=480
∴ x=9.6
答:9.6小时后快车追上慢车。
(5)分析:追及问题,相等关系与(4)类似。
解:设快车开出x小时后追上慢车。
由题意得,140x=90(x+1)+480
50x=570
∴ x=11.4
答:快车开出11.4小时后追上慢车。
例12:甲、乙二人同时从A地去往相距51千米的B地,甲骑车,乙步行,甲的速度比乙的速度快3倍还多1千米/时,甲到达B地后停留1小时,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好6个小时,求二人速度各是多少?
分析:本题属于相遇问题,用图表示(甲用实线,乙用虚线表示)。注意:甲在B地还停留1小时。A、B两地相距51千米。
等量关系为:甲走路程+乙走路程=51×2。
解:设乙速为x千米/小时,则甲速为(3x+1)千米/小时,
由题意得,6x+(3x+1)(6-1)=51×2
∴ x=5
3x+1=15+1=16
答:甲速为16千米/时,乙速为5千米/时。
例13:某船从A码头顺流而下到达B码头,然后逆流返回,到达A、B两码头之间的C码头,一共航行了7小时,已知此船在静水中的速度为7.5千米时,水流速度为2.5千米/时。A、C两码头之间的航程为10千米,求A、B两码头之间的航程。
分析:这属于行船问题,这类问题中要弄清(1)顺水速度=船在静水中的速度+水流速度,(2)逆水速度=船在静水中的速度-水流速度。相等关系为:顺流航行的时间+逆流航行的时间=7小时。
解:设A、B两码头之间的航程为x千米,则B、C间的航程为(x-10)千米,
由题意得,+=7
∴ x=30
答:A、B两码头之间的航路为30千米。
例14:环城自行车赛,最快的人在开始48分钟后遇到最慢的人,已知最快的人的速度是最慢的人速度的3倍,环城一周是20千米,求两个人的速度。
分析:这是环形问题,本题类似于追及问题,距离差为环城一周20千米。相等关系为:最快的人骑的路程-最慢人骑的路程=20千米。
解;设最慢的人速度为x千米/时,则最快的人的速度为x千米/时,
由题意得,x×-x×=20
x=35
答:最快的人的速度为35千米/时,最慢的人的速度为10千米/时。
8、配套问题:
[解题指导]:这类问题的关键是找对配套的两类物体的数量关系。
例15:某车间有工人85人,平均每人每天可以加工大齿轮8个或小齿轮10个,又知1个大齿轮和三个小齿轮配为一套,问应如何安排劳力使生产的产品刚好成套?
分析:这个问题的等量关系为:小齿轮个数=3倍大齿轮个数
解:设应安排x个工人加工大齿轮,则有(85-x)个工人加工小齿轮,
由题意得,(85-x)×10=3×8x
解这个方程,850-10x=24x
34x=850
∴ x=25
85-x=85-25=60
答:应安排25个工人加工大齿轮,其余60人加工小齿轮,才能使生产的产品刚好成套。
9、其他实际应用问题:
[解题指导]这类问题的关键是理解所给问题中的实际关系
例16:银行定期壹年存款的年利率为2.5%,某人存入一年后本息922.5元,问存入银行的本金是多少元?
分析:这里的相等关系为:
本息和=本金+利息=本金+本金×利率×期数
解:设存入银行的本金是x元,
由题意得,922.5=x+x×2.5%×1
解这个方程,1.025x=922.5
∴ x=900(元)
答:存入银行的本金是900元。
例17:某商品的进价为1600元,原售价为2200元因库存积压需降价出售,若每件商品仍想获得10%的利润需几折出售。
分析:等量关系为:原价×折扣=进价×(1+10%)
解:设需x折出售,
由题意得,2200×=1600(1+10%)
220x=1600×1.10
x=8
答:需8折出售。
例18:已知甲、乙两种商品的原单价和为100元。因市场变化,甲商品降价10%,乙商品提价5%,调价后,甲、乙两种商品的单价和比原单价和提高了2%,求甲、乙两种商品的原单价各是多少?
分析:甲原单价×(1-10%)+乙原单价×(1+5%)=100×(1+2%)。
解:设甲商品原单价为x 元,则乙商品原单价为(100-x)元。
由题意得,(1-10%)x+(1+5%)(100-x)=100×(1+2%)
∴ x=20
100-x=80
答:甲商品原单价20元,乙商品原单价为80元。
注意:虽然我们分了9种类型,对应用题进行了研究,但实际生活中的问题是千变万化的,远不止这9类问题。因此我们要想学好列方程解应用题,就要学会观察事物,关心日常生产生活中的各种问题,如市场经济问题等等,要会具体情况具体分析,灵活运用所学知识,认真审题,适当设元,寻找等量关系,从而列出方程,解出方程,使问题得解
设间接未知数
一、求整体时,可设其中的某部分为未知数
例1 一个两位数,十位上的数字与个位上的数字之和为11,如果把十位上的数字与个位上的数字对调,那么得到的新数就比原数大63,求原来的两位数。
分析 此题若直接设原来两位数为未知数,显然不易求解,对这种求整体的问题可设其中的某部分为未知数,这样可使问题获得简便的解答。
略解 设原来的两位数个位上的数字为x,则十位上的数字为11-x,
由题意有:10x+ll-x=10(11-x)+x+63,解得x=9。
答:所求两位数为29。
二、若求其中的某部分时,可设其整体为未知数
例2 某三个数中每两个数之和分别为27、28、29,求这三个数。
分析 这是求部分的问题,如果直接设这三个数分别x、y, z,就要列出一个三元一次方程组,但若采用间接设元法设这三个数的和为未知数,问题就变得异常简捷。
略解 设这三个数的和为x,则这三个数分别为x-27、x-28、x-29,
由题意有:(x-27)+(x-28)+(x-29)=x,解得x=42。
答:这三个数分别为15、14、13。
三、当题设条件中含有“比”时,通常可设其中的一份为x
例3 甲、乙、丙三数的比为7:9:12,甲、乙两数的和减去丙数的差等于20求此三数。
分析 因为7+9+12=28,说明三数的和为28份,甲、乙、丙分别占7份、9份、12份,这样,可设每份为x,
则甲、乙、丙三数分别为7x、9x、12x,由题意得:7x+9x-12x=20,以下略。
四、设而不求,巧用间接未知数“过渡”
解应用题必须对题目的条件和关系进行深入的分析,认真的思考,然后合理地选择未知数,并注意发挥未知数的桥梁“过渡”作用,才能使复杂的问题变得简单,从而促成问题的解决。
例4 有甲、乙、丙三种货物,若购甲3件、乙7件、丙1件共需3.15元;若购甲4件、乙10件、丙1件共需4.20元。问购甲、乙、丙各1件共需多少元
分析 若直接设购甲、乙、丙各1件共需n元,则列方程较为繁难,而若设甲、乙、丙三种货物的单价分别为x、y、z元,则由题意有:
由于本题的要求是求出x+y+z,因此我们可以不去求x、y、z的具体值(设而不求),而采用整体化的数学思想,直接求出结果:
将方程组变形为
,
解之得x+y+z=1.05。(注:本题有点难)
五、直难则间,妙用间接未知数“转换”
解决较为复杂的应用题,在直接设元布列方程感到困难时,应及时变换思考的角度,调整和转变原有的思想和方法,合理地设置间接未知数设法进行转化,以寻求新的解决问题的途径和方法。
例5 四盘苹果共100个,把第一盘的个数加上4,第二盘的个数减去4,第三盘的个数乘以4,第四盘的个数除以4,所得的数目一样,问原来四盘苹果各多少个
分析 本题若从四盘苹果考虑直接设未知数,需要列出四元一次方程组,解起来不胜繁难。如果由“所得的数目一样”这个条件逆想,则由此可推出四盘苹果的数目,因此,设间接未知数x表示这个数目,则容易得到四盘苹果原来的个数分别为x-4, x+4, , 4x, 于是很方便地列出方程:(x-4)+(x+4)++4x=100。以下略。
设间接未知数解应用题,当然不限于上述几种情况,但由上足见选择适当的间接未知数在列方程解应用题中的重要作用,同学们应给以足够的重视
典型应用题练习
1.某车间原计划每周装配36台机床,预计若干周完成任务。在装配了三分之一以后,改进操作技术,工效提高了一倍,结果提前一周半完成任务。求这次任务需装配机床总台数。
2.某班同学参加平整土地劳动,运土人数比挖土人数的一半多3人。若从挖土人员中抽出6人运土,则两者人数相等。求原来运土和挖土各多少人。
3.某年级三个班为灾区捐款。(1)班捐了380元,(2)班捐款数是另两个班级的平均数,(3)班捐款数是三个班总数的,求(2)班,(3)班捐款数。
4.一轮船航行于两个码头之间,逆水需10小时,顺水需6小时。已知该船在静水中每小时航行12千米,求水流速度和两码头间的距离。
5.有一批长度均为50厘米的铁锭,截面都是长方形,一边长10厘米,另一边各不相同,现要铸造一个42.9千克的零件,应选截面另一边长为多少的铁锭(铁锭每立方厘米重7.8克)?
6.甲、乙两人在400米环形跑道上练习长跑,两人速度分别为200米/分和160米/分。两人同时从起点同向出发。当两人起跑后第一次并肩时经过了多少时间?这时他们各跑了多少圈?
7.检修一处住宅区的自来水管道,甲单独完成需14天,乙单独完成需18天,丙单独完成需12天。前7天由甲、乙两人合做,但乙中途离开了一段时间,后2天由乙、丙合作完成。问乙中途离开了几天?
8.某商场甲、乙两个柜组十二月份营业额共64万元。一月份甲增长了20%,乙增长了15%,营业额共达到75万元。求两柜组各增长多少万元。
9.某行军纵队以8千米/时的速度行进,队尾的通讯员以12千米/时的速度赶到队伍前送一个文件。送到后立即返回队尾,共用14.4分钟。求队伍长。
10.一个两位数,十位数比个位数字的4倍多1。将两个数字调换顺序后所得数比原数小63。求原数。
11.一桥长1000米,一列火车从车头上桥到车尾离桥用了一分钟时间,整列火车完全在桥上的时间为40秒。求火车的长度及行驶速度。
12.甲从学校出发到相距14千米的A地。当到达距学校2千米的B地时发现遗忘某物品。打电话给乙,乙随即出发在C地追上甲后立即返回。当乙回到学校时甲距A地还有3千米。求学校到C地的距离。
一、列方程解应用题的主要步骤:
1、认真审题,理解题意,弄清题目中的数量关系,找出其中的等量关系;
2、用字母表示题目中的未知数,并用这个字母和已知数一起组成表示各数量关系的代数式;
3、利用这些代数式列出反映某个等量关系的方程(注意所使用的单位一定要统一);
4、求出所列方程的解;
5、检验所求的解是否使方程成立,又能使应用题有意义,并写出答案。
二、对常见应用题的解法分析
1、和、差、倍、分问题;这类问题主要应搞清各量之间的关系,注意关键词语。(1)倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率……”来体现。(2)多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。
例2、旅行社的一辆汽车在第一次旅程中用去油箱里汽油的25%,第二次旅程中用去剩余汽油的40%,这样油箱中剩的汽油比两次所用的汽油少1公斤,求油箱里原有汽油多少公斤?
分析:等量关系为:油箱中剩余汽油+1=用去的汽油。
解:设油箱里原有汽油x公斤,
由题意得,x(1-25%)(1-40%)+1=25%x+(1-25%)x×40%
∴ x=10
答:油箱里原有汽油10公斤。
2、等积变形问题:
“等积变形”是以形状改变而体积不变为前提。常用等量关系为:原料体积=成品体积。
例3、现有直径为0.8米的圆柱形钢坯30米,可足够锻造直径为0.4米,长为3米的圆柱形机轴多少根?
分析:等量关系为:机轴的体积和=钢坯的体积。
解:设可足够锻造x根机轴,
由题意得,π()2×3x=π()2×30
x=×10×==40
答:可足够锻造直径为0.4米,长为3米的圆柱形机轴40根。
3、劳力调配问题:
这类问题要搞清人数的变化,常见题型有(1)既有调入又有调出。(2)只有调入没有调出,调入部分变化,其余不变;(3)只有调出没有调入,调出部分变化,其余不变。
例4、有两个工程队,甲队有285人,乙队有183人,若要求乙队人数是甲队人数的,应从乙队调多少人到甲队?
分析:此问题中对乙队来说有调出,对甲队来说有调入。等量关系为:乙队调出后人数=甲队调入后人数。
解:设应从乙队调x人到甲队,
由题意得,183-x=(285+x)
解这个方程,285+x=549-3x
4x=264
∴ x=66
答:应从乙队调66人到甲队。
例5、甲、乙两个工程队分别有188人和138人,现需要从两队抽出116人组成第三个队,并使甲、乙两队剩余人数之比为2:1,问应从甲、乙两队各抽出多少人?
分析:此问题中只有调出,没有调入。等量关系为:甲队调出后人数=2×乙队调出后人数。
解:设应从甲队抽出x人,则应从乙队抽出(116-x)人,
由题意得,188-x=2[138-(116-x)]
解这个方程188-x=2(138-116+x)
188-x=44+2x
3x=144
∴ x=48
116-x=116-48=68
答:应从甲队抽出48人,从乙队抽出68人。
4、比例分配问题:
这类问题的一般思路为:设其中一份为x ,利用已知的比,写出相应的代数式。
常用等量关系:各部分之和=总量。
例7、甲、乙、丙三个人每天生产机器零件数为甲、乙之比为4:3;乙、丙之比为6:5,又知甲与丙的和比乙的2倍多12件,求每个人每天生产多少件?
分析:应设一份为x件,则其他量均可用含x的代数式表示。等量关系为:(甲日产量+丙日产量)-12=乙日产量的2倍。
解:设一份为x件,则甲每天生产4x件,乙每天生产3x件,丙每天生产×3x件(即x件),
由题意得,4x+x-12=2×3x
解这个方程,=12
∴ x=24
∴ 4x=4×24=96(件),3x=3×24=72(件),x=×24=60(件)
答:甲每天生产96件,乙每天生产72件,丙每天生产60件。
5、数字问题:
要搞清楚数的表示方法:一个三位数的百位数字为a,十位数字是b,个位数字为c(其中a、b、c均为整数,且
1≤a≤9, 0≤b≤9, 0≤c≤9)则这个三位数表示为:100a+10b+c。
例8、一个2位数,个位上的数字比十位上的数学大5,且个位上的数字与十位上的数字的和比这个2位数的大6,求这个2位数。
分析:等量关系为:个位数字+十位数字-6=×这个2位数。
解:设十位上的数字为x,则个位上的数字为x+5,
则这个2位数为:10x+x+5
由题意得,x+5+x-6=(10x+x+5)
∴ x=4
∴ x+5=9
这个2位数为49。
6、工程问题:
工程问题中的三个量及其关系为:工作总量=工作效率×工作时间
经常在题目中未给出工作总量时,设工作总量为单位1。
例9、一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
分析:设工程总量为单位1,等量关系为:甲完成工作量+乙完成工作量=工作总量。
解:设乙还需x天完成全部工程,设工作总量为单位1,
由题意得,(+)×3+=1,
∴ x==6
答:乙还需6天才能完成全部工程。
例10、一个蓄水池有甲、乙两个进水管和一个丙排水管,单独开甲管6小时可注满水池;单位开乙管8小时可注满水池,单独开丙管9小时可将满池水排空,若先将甲、乙管同时开放2小时,然后打开丙管,问打开丙管后几小时可注满水池?
分析:等量关系为:甲注水量+乙注水量-丙排水量=1。
解:设打开丙管后x小时可注满水池,
由题意得,(+)(x+2)-=1
13x=30
∴ x==2
答:打开丙管后2小时可注满水池
真题专练:
1.(河北省)某种收音机,原来每台售价48元,降价后每台售价42元,则降价的百分数为________。
2.(湖南长沙)国家规定储蓄存款需征收利息税,利息税的税率是20%(即储蓄利息的20%)。小红在银行存入人民币二万元,定期一年,年息为432元,存款到期时,应交利息税________元。
3.(江苏南京)有一旅客携带了30公斤行李从南京禄口国际机场乘飞机去天津,按民航规定,旅客最多可免费携带20公斤行李,超重部分每公斤按飞机票价格的1.5%购买行李票,现该旅客购买了120元的行李票,则他的飞机 票价格应是( )
A、1000元 B、800元 C、600元 D、400元
5.(北京西城区)一个角的余角比它的补角的还少20°,求这个角。
6.(吉林省)某初一学生在做作业时,不慎将墨水瓶打翻,使一道作业题只看到如下字样:“甲、乙两地相距40千米,摩托车的速度为45千米/时,运货汽车的速度为35千米/时,〓〓 (涂黑部分表示被墨水覆盖的若干文字)请将这道作业题补充完整,并列方程解答。
8.(安徽省)目前,包括长江、黄河等七大流域在内,全国水土流失面积达到367万平方千米,其中长江与黄河流域的水土流失总面积占全国的32.4%。而长江流域的水土流失问题更为严重,它的水土流失面积比黄河流域的水土流失面积还要多29万平方千米。问长江流域的水土流失面积是多少?(结果保留整数)
7、行程问题:
[解题指导]
(1)行程问题中的三个基本量及其关系: 路程=速度×时间。
(2)基本类型有
1)相遇问题;
2)追及问题;常见的还有:相背而行;行船问题;环形跑道问题。
(3)解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系,一般情况下问题就能迎刃而解。并且还常常借助画草图来分析,理解行程问题。
例11:甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
(1)慢车先开出1小时,快车再开。两车相向而行。问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600公里?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里?
(4)两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
(5)慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车?
此题关键是要理解清楚相向.相背.同向等的含义,弄清行驶过程。故可结合图形分析。
(1)分析:相遇问题,画图表示为:
等量关系是:慢车走的路程+快车走的路程=480公里。
解:设快车开出x小时后两车相遇,
由题意得,140x+90(x+1)=480
解这个方程,230x=390
∴ x=1
答:快车开出1小时两车相遇。
(2)分析:相背而行,画图表示为:
等量关系是:两车所走的路程和+480公里=600公里。
解:设x小时后两车相距600公里,
由题意得,(140+90)x+480=600
解这个方程,230x=120
∴ x=
答:小时后两车相距600公里。
(3)分析:等量关系为:快车所走路程-慢车所走路程+480公里=600公里。
解:设x小时后两车相距600公里,
由题意得,(140-90)x+480=600
50x=120
∴ x=2.4
答:2.4小时后两车相距600公里。
(4)分析;追及问题,画图表示为:
等量关系为:快车的路程=慢车走的路程+480公里。
解:设x小时后快车追上慢车。
由题意得,140x=90x+480
解这个方程,50x=480
∴ x=9.6
答:9.6小时后快车追上慢车。
(5)分析:追及问题,相等关系与(4)类似。
解:设快车开出x小时后追上慢车。
由题意得,140x=90(x+1)+480
50x=570
∴ x=11.4
答:快车开出11.4小时后追上慢车。
例12:甲、乙二人同时从A地去往相距51千米的B地,甲骑车,乙步行,甲的速度比乙的速度快3倍还多1千米/时,甲到达B地后停留1小时,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好6个小时,求二人速度各是多少?
分析:本题属于相遇问题,用图表示(甲用实线,乙用虚线表示)。注意:甲在B地还停留1小时。A、B两地相距51千米。
等量关系为:甲走路程+乙走路程=51×2。
解:设乙速为x千米/小时,则甲速为(3x+1)千米/小时,
由题意得,6x+(3x+1)(6-1)=51×2
∴ x=5
3x+1=15+1=16
答:甲速为16千米/时,乙速为5千米/时。
例13:某船从A码头顺流而下到达B码头,然后逆流返回,到达A、B两码头之间的C码头,一共航行了7小时,已知此船在静水中的速度为7.5千米时,水流速度为2.5千米/时。A、C两码头之间的航程为10千米,求A、B两码头之间的航程。
分析:这属于行船问题,这类问题中要弄清(1)顺水速度=船在静水中的速度+水流速度,(2)逆水速度=船在静水中的速度-水流速度。相等关系为:顺流航行的时间+逆流航行的时间=7小时。
解:设A、B两码头之间的航程为x千米,则B、C间的航程为(x-10)千米,
由题意得,+=7
∴ x=30
答:A、B两码头之间的航路为30千米。
例14:环城自行车赛,最快的人在开始48分钟后遇到最慢的人,已知最快的人的速度是最慢的人速度的3倍,环城一周是20千米,求两个人的速度。
分析:这是环形问题,本题类似于追及问题,距离差为环城一周20千米。相等关系为:最快的人骑的路程-最慢人骑的路程=20千米。
解;设最慢的人速度为x千米/时,则最快的人的速度为x千米/时,
由题意得,x×-x×=20
x=35
答:最快的人的速度为35千米/时,最慢的人的速度为10千米/时。
8、配套问题:
[解题指导]:这类问题的关键是找对配套的两类物体的数量关系。
例15:某车间有工人85人,平均每人每天可以加工大齿轮8个或小齿轮10个,又知1个大齿轮和三个小齿轮配为一套,问应如何安排劳力使生产的产品刚好成套?
分析:这个问题的等量关系为:小齿轮个数=3倍大齿轮个数
解:设应安排x个工人加工大齿轮,则有(85-x)个工人加工小齿轮,
由题意得,(85-x)×10=3×8x
解这个方程,850-10x=24x
34x=850
∴ x=25
85-x=85-25=60
答:应安排25个工人加工大齿轮,其余60人加工小齿轮,才能使生产的产品刚好成套。
9、其他实际应用问题:
[解题指导]这类问题的关键是理解所给问题中的实际关系
例16:银行定期壹年存款的年利率为2.5%,某人存入一年后本息922.5元,问存入银行的本金是多少元?
分析:这里的相等关系为:
本息和=本金+利息=本金+本金×利率×期数
解:设存入银行的本金是x元,
由题意得,922.5=x+x×2.5%×1
解这个方程,1.025x=922.5
∴ x=900(元)
答:存入银行的本金是900元。
例17:某商品的进价为1600元,原售价为2200元因库存积压需降价出售,若每件商品仍想获得10%的利润需几折出售。
分析:等量关系为:原价×折扣=进价×(1+10%)
解:设需x折出售,
由题意得,2200×=1600(1+10%)
220x=1600×1.10
x=8
答:需8折出售。
例18:已知甲、乙两种商品的原单价和为100元。因市场变化,甲商品降价10%,乙商品提价5%,调价后,甲、乙两种商品的单价和比原单价和提高了2%,求甲、乙两种商品的原单价各是多少?
分析:甲原单价×(1-10%)+乙原单价×(1+5%)=100×(1+2%)。
解:设甲商品原单价为x 元,则乙商品原单价为(100-x)元。
由题意得,(1-10%)x+(1+5%)(100-x)=100×(1+2%)
∴ x=20
100-x=80
答:甲商品原单价20元,乙商品原单价为80元。
注意:虽然我们分了9种类型,对应用题进行了研究,但实际生活中的问题是千变万化的,远不止这9类问题。因此我们要想学好列方程解应用题,就要学会观察事物,关心日常生产生活中的各种问题,如市场经济问题等等,要会具体情况具体分析,灵活运用所学知识,认真审题,适当设元,寻找等量关系,从而列出方程,解出方程,使问题得解
设间接未知数
一、求整体时,可设其中的某部分为未知数
例1 一个两位数,十位上的数字与个位上的数字之和为11,如果把十位上的数字与个位上的数字对调,那么得到的新数就比原数大63,求原来的两位数。
分析 此题若直接设原来两位数为未知数,显然不易求解,对这种求整体的问题可设其中的某部分为未知数,这样可使问题获得简便的解答。
略解 设原来的两位数个位上的数字为x,则十位上的数字为11-x,
由题意有:10x+ll-x=10(11-x)+x+63,解得x=9。
答:所求两位数为29。
二、若求其中的某部分时,可设其整体为未知数
例2 某三个数中每两个数之和分别为27、28、29,求这三个数。
分析 这是求部分的问题,如果直接设这三个数分别x、y, z,就要列出一个三元一次方程组,但若采用间接设元法设这三个数的和为未知数,问题就变得异常简捷。
略解 设这三个数的和为x,则这三个数分别为x-27、x-28、x-29,
由题意有:(x-27)+(x-28)+(x-29)=x,解得x=42。
答:这三个数分别为15、14、13。
三、当题设条件中含有“比”时,通常可设其中的一份为x
例3 甲、乙、丙三数的比为7:9:12,甲、乙两数的和减去丙数的差等于20求此三数。
分析 因为7+9+12=28,说明三数的和为28份,甲、乙、丙分别占7份、9份、12份,这样,可设每份为x,
则甲、乙、丙三数分别为7x、9x、12x,由题意得:7x+9x-12x=20,以下略。
四、设而不求,巧用间接未知数“过渡”
解应用题必须对题目的条件和关系进行深入的分析,认真的思考,然后合理地选择未知数,并注意发挥未知数的桥梁“过渡”作用,才能使复杂的问题变得简单,从而促成问题的解决。
例4 有甲、乙、丙三种货物,若购甲3件、乙7件、丙1件共需3.15元;若购甲4件、乙10件、丙1件共需4.20元。问购甲、乙、丙各1件共需多少元
分析 若直接设购甲、乙、丙各1件共需n元,则列方程较为繁难,而若设甲、乙、丙三种货物的单价分别为x、y、z元,则由题意有:
由于本题的要求是求出x+y+z,因此我们可以不去求x、y、z的具体值(设而不求),而采用整体化的数学思想,直接求出结果:
将方程组变形为
,
解之得x+y+z=1.05。(注:本题有点难)
五、直难则间,妙用间接未知数“转换”
解决较为复杂的应用题,在直接设元布列方程感到困难时,应及时变换思考的角度,调整和转变原有的思想和方法,合理地设置间接未知数设法进行转化,以寻求新的解决问题的途径和方法。
例5 四盘苹果共100个,把第一盘的个数加上4,第二盘的个数减去4,第三盘的个数乘以4,第四盘的个数除以4,所得的数目一样,问原来四盘苹果各多少个
分析 本题若从四盘苹果考虑直接设未知数,需要列出四元一次方程组,解起来不胜繁难。如果由“所得的数目一样”这个条件逆想,则由此可推出四盘苹果的数目,因此,设间接未知数x表示这个数目,则容易得到四盘苹果原来的个数分别为x-4, x+4, , 4x, 于是很方便地列出方程:(x-4)+(x+4)++4x=100。以下略。
设间接未知数解应用题,当然不限于上述几种情况,但由上足见选择适当的间接未知数在列方程解应用题中的重要作用,同学们应给以足够的重视
典型应用题练习
1.某车间原计划每周装配36台机床,预计若干周完成任务。在装配了三分之一以后,改进操作技术,工效提高了一倍,结果提前一周半完成任务。求这次任务需装配机床总台数。
2.某班同学参加平整土地劳动,运土人数比挖土人数的一半多3人。若从挖土人员中抽出6人运土,则两者人数相等。求原来运土和挖土各多少人。
3.某年级三个班为灾区捐款。(1)班捐了380元,(2)班捐款数是另两个班级的平均数,(3)班捐款数是三个班总数的,求(2)班,(3)班捐款数。
4.一轮船航行于两个码头之间,逆水需10小时,顺水需6小时。已知该船在静水中每小时航行12千米,求水流速度和两码头间的距离。
5.有一批长度均为50厘米的铁锭,截面都是长方形,一边长10厘米,另一边各不相同,现要铸造一个42.9千克的零件,应选截面另一边长为多少的铁锭(铁锭每立方厘米重7.8克)?
6.甲、乙两人在400米环形跑道上练习长跑,两人速度分别为200米/分和160米/分。两人同时从起点同向出发。当两人起跑后第一次并肩时经过了多少时间?这时他们各跑了多少圈?
7.检修一处住宅区的自来水管道,甲单独完成需14天,乙单独完成需18天,丙单独完成需12天。前7天由甲、乙两人合做,但乙中途离开了一段时间,后2天由乙、丙合作完成。问乙中途离开了几天?
8.某商场甲、乙两个柜组十二月份营业额共64万元。一月份甲增长了20%,乙增长了15%,营业额共达到75万元。求两柜组各增长多少万元。
9.某行军纵队以8千米/时的速度行进,队尾的通讯员以12千米/时的速度赶到队伍前送一个文件。送到后立即返回队尾,共用14.4分钟。求队伍长。
10.一个两位数,十位数比个位数字的4倍多1。将两个数字调换顺序后所得数比原数小63。求原数。
11.一桥长1000米,一列火车从车头上桥到车尾离桥用了一分钟时间,整列火车完全在桥上的时间为40秒。求火车的长度及行驶速度。
12.甲从学校出发到相距14千米的A地。当到达距学校2千米的B地时发现遗忘某物品。打电话给乙,乙随即出发在C地追上甲后立即返回。当乙回到学校时甲距A地还有3千米。求学校到C地的距离。
