2020—2021学年人教版数学八年级下册 18.1.2.2 三角形的中位线定理 课件(共13张ppt)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册 18.1.2.2 三角形的中位线定理 课件(共13张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 529.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 21:03:03 | ||
图片预览

文档简介
(共13张PPT)
三角形的中位线
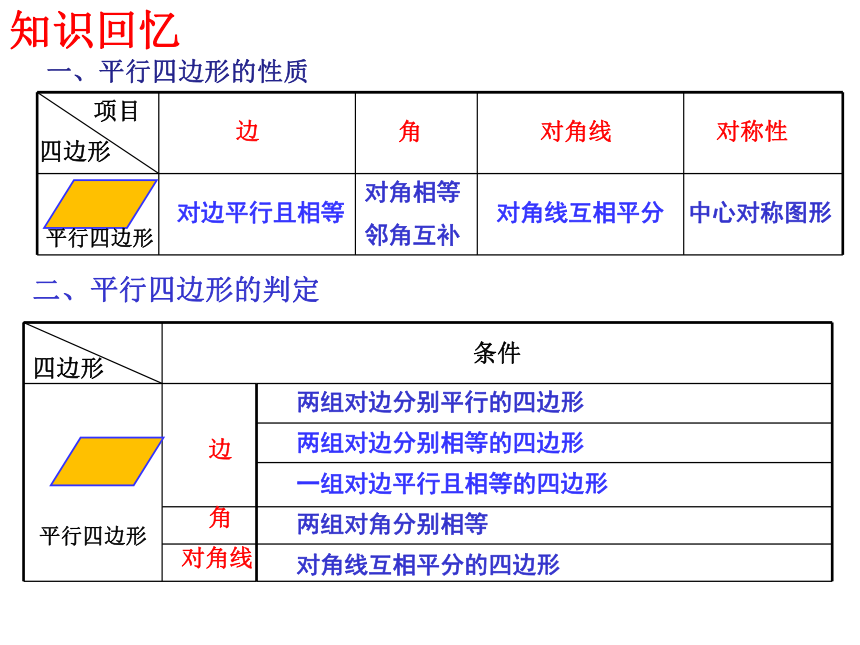
一、平行四边形的性质
对边平行且相等
对角相等
邻角互补
对角线互相平分
中心对称图形
条件
知识回忆
两组对边分别平行的四边形
两组对边分别相等的四边形
一组对边平行且相等的四边形
两组对角分别相等
对角线互相平分的四边形
二、平行四边形的判定
项目
四边形
平行四边形
边
角
对角线
对称性
四边形
边
角
对角线
平行四边形
D
C
B
A
E
FF
F
XIAN现有YOU现有
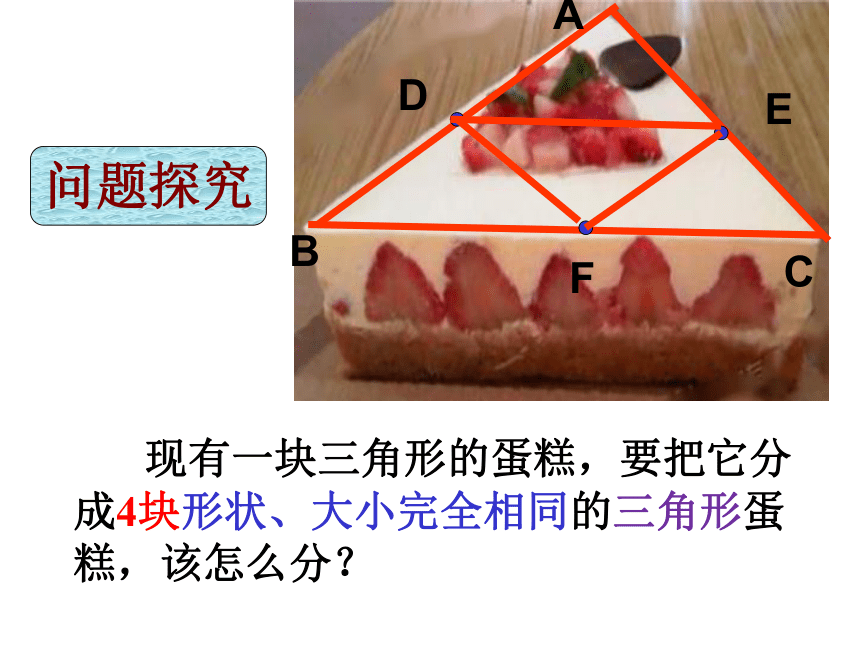
现有一块三角形的蛋糕,要把它分成4块形状、大小完全相同的三角形蛋糕,该怎么分?
问题
问题探究
D
C
B
A
E
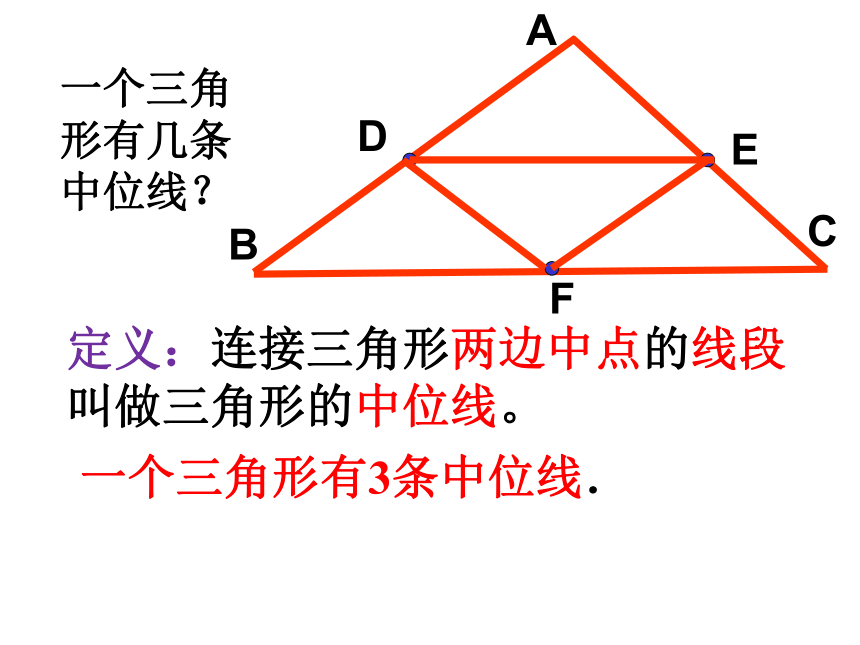
定义:连接三角形两边中点的线段叫做三角形的中位线。
一个三角形有3条中位线.
F
一个三角形有几条中位线?
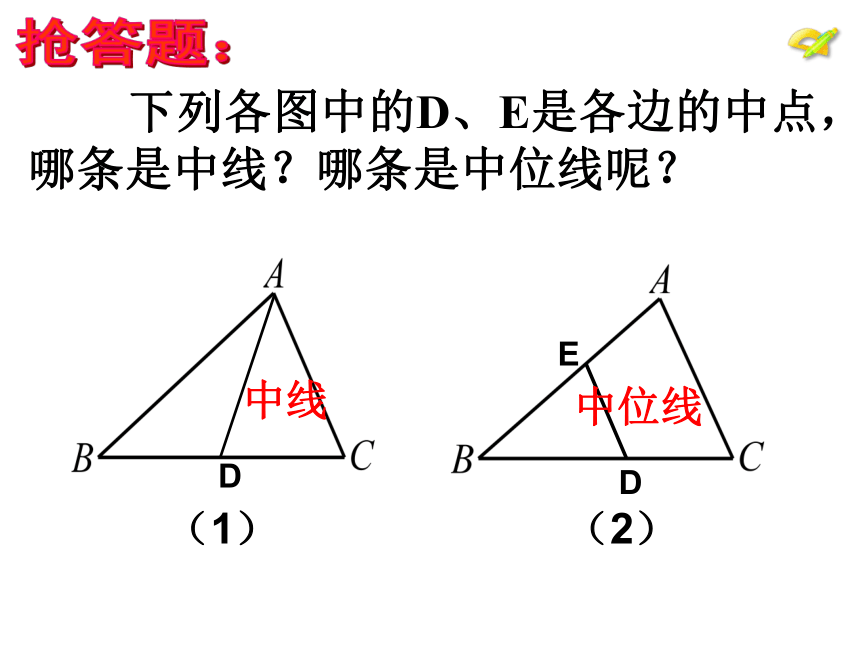
下列各图中的D、E是各边的中点,哪条是中线?哪条是中位线呢?
抢答题:
E
D
D
(1))
(2))
中线
中线
中位线
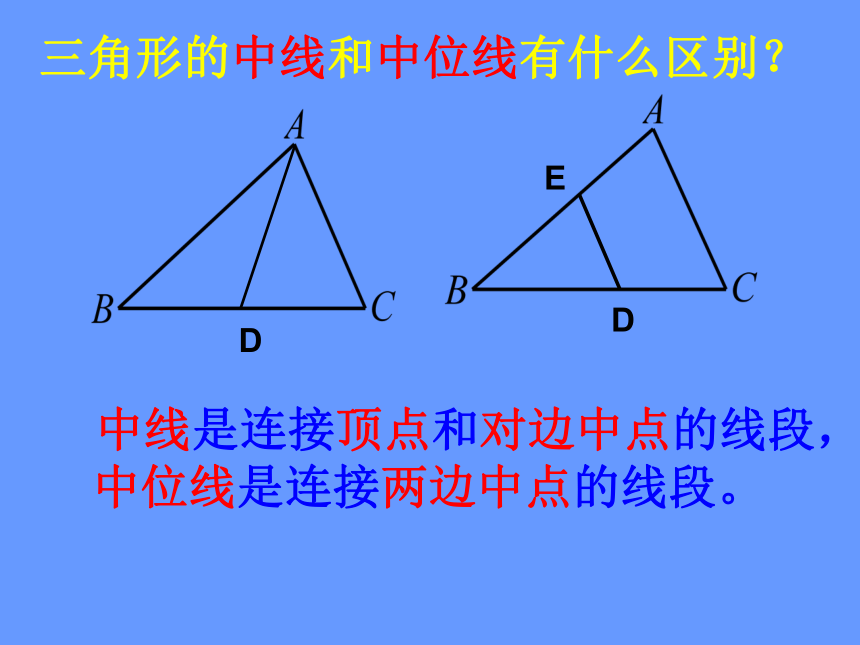
三角形的中线和中位线有什么区别?
中线是连接顶点和对边中点的线段,
中位线是连接两边中点的线段。
D
E
D
D
C
B
A
E
△ABC 的中位线DE与边BC有什么样的位置关系和数量关系?
三角形的中位线平行于第三边,并且等于第三边的一半。
猜想:
如何证明?
猜一猜
A
B
C
D
E
F
例1.如图,点D、E分别是△ABC的边AB、AC的中点,求证:DE∥BC且DE= BC
证明:
延长DE至F,使EF=DE,连接DC、CF、AF
∵ E是AC的中点
∴ AE=CE
∵ EF=DE
∴四边形ADCF是平行四边形
∴ DE ∥ BC
DF=BC
∵DE=EF ,DE+EF=DF
∴ DE= DF
∴ DE= BC
∴ AD ∥ FC,AD=FC
∵ D是AB的中点
∴ BD=AD
∴ BD ∥ FC,BD=FC
∴四边形BCFD是平行四边形
三角形的中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半.
用符号语言表示
E
A
B
C
D
∵DE是△ABC的中位线
∴ DE ∥ BC且DE= BC
∵ AD=BD,AE=CE
∴DE ∥ BC且DE= BC
∵D是AB的中点,E是AC的中点∴DE ∥ BC且DE= BC
A
C
B
E
D
F
大显身手
2.如图,在△ABC中,D、E分别是AB、AC的中点
若∠ADE=65°,则∠B= 度,为什么?
若BC=8cm,则DE= cm,为什么?
65
4
若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______
3.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24,△DEF的周长是_____
12
三角形三条中位线围成的三角形的周长是原三角形周长的 。
情境再现
图中有_____个平行四边形
3
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
三角形问题
转化
智慧的运用:
规律总结:连接任意四边形四边的中点,得到的图形(中点四边形)是平行四边形.
本节课你学习了什么?
三角形中位线定理:
三角形的中位线 于三角形的第三边,并且等于第三边的 。
智慧的反思
平行
一半
三角形中位线的定义:
连接三角形两边 的 叫做三角形的
中点
线段
中位线。
1、P49练习题第3题;
2、P62第16题。
作业
三角形的中位线
一、平行四边形的性质
对边平行且相等
对角相等
邻角互补
对角线互相平分
中心对称图形
条件
知识回忆
两组对边分别平行的四边形
两组对边分别相等的四边形
一组对边平行且相等的四边形
两组对角分别相等
对角线互相平分的四边形
二、平行四边形的判定
项目
四边形
平行四边形
边
角
对角线
对称性
四边形
边
角
对角线
平行四边形
D
C
B
A
E
FF
F
XIAN现有YOU现有
现有一块三角形的蛋糕,要把它分成4块形状、大小完全相同的三角形蛋糕,该怎么分?
问题
问题探究
D
C
B
A
E
定义:连接三角形两边中点的线段叫做三角形的中位线。
一个三角形有3条中位线.
F
一个三角形有几条中位线?
下列各图中的D、E是各边的中点,哪条是中线?哪条是中位线呢?
抢答题:
E
D
D
(1))
(2))
中线
中线
中位线
三角形的中线和中位线有什么区别?
中线是连接顶点和对边中点的线段,
中位线是连接两边中点的线段。
D
E
D
D
C
B
A
E
△ABC 的中位线DE与边BC有什么样的位置关系和数量关系?
三角形的中位线平行于第三边,并且等于第三边的一半。
猜想:
如何证明?
猜一猜
A
B
C
D
E
F
例1.如图,点D、E分别是△ABC的边AB、AC的中点,求证:DE∥BC且DE= BC
证明:
延长DE至F,使EF=DE,连接DC、CF、AF
∵ E是AC的中点
∴ AE=CE
∵ EF=DE
∴四边形ADCF是平行四边形
∴ DE ∥ BC
DF=BC
∵DE=EF ,DE+EF=DF
∴ DE= DF
∴ DE= BC
∴ AD ∥ FC,AD=FC
∵ D是AB的中点
∴ BD=AD
∴ BD ∥ FC,BD=FC
∴四边形BCFD是平行四边形
三角形的中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半.
用符号语言表示
E
A
B
C
D
∵DE是△ABC的中位线
∴ DE ∥ BC且DE= BC
∵ AD=BD,AE=CE
∴DE ∥ BC且DE= BC
∵D是AB的中点,E是AC的中点∴DE ∥ BC且DE= BC
A
C
B
E
D
F
大显身手
2.如图,在△ABC中,D、E分别是AB、AC的中点
若∠ADE=65°,则∠B= 度,为什么?
若BC=8cm,则DE= cm,为什么?
65
4
若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______
3.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24,△DEF的周长是_____
12
三角形三条中位线围成的三角形的周长是原三角形周长的 。
情境再现
图中有_____个平行四边形
3
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
三角形问题
转化
智慧的运用:
规律总结:连接任意四边形四边的中点,得到的图形(中点四边形)是平行四边形.
本节课你学习了什么?
三角形中位线定理:
三角形的中位线 于三角形的第三边,并且等于第三边的 。
智慧的反思
平行
一半
三角形中位线的定义:
连接三角形两边 的 叫做三角形的
中点
线段
中位线。
1、P49练习题第3题;
2、P62第16题。
作业
